Advances in Applied Mathematics
Vol.07 No.07(2018), Article ID:26144,16
pages
10.12677/AAM.2018.77109
Dynamic Analysis of Predator-Prey System with Allee Effect and State Control
Kaili Ma
College of Mathematics, Physics and Electronic Information Engineering, Wenzhou University, Wenzhou Zhejiang
Received: Jul. 5th, 2018; accepted: Jul. 23rd, 2018; published: Jul. 30th, 2018

ABSTRACT
In this paper, a predator-prey system with Allee effect and state control is constructed under the framework of biological control strategy. The existence and stability criteria of semi-trivial periodic solution are established, and the properties of their solutions, such as existence, uniqueness, stability and periodicity are discussed. At the same time, the related dynamic behavior of the system is numerically simulated to verify the validity of the theoretical results.
Keywords:Prey-Predator System, Allee Effect, State Control, Periodic Solution
具有Allee效应和状态控制的捕食–食饵系统的动力学分析
马凯丽
温州大学,数理与电子信息工程学院,浙江 温州
收稿日期:2018年7月5日;录用日期:2018年7月23日;发布日期:2018年7月30日

摘 要
在生物控制策略研究框架下,构建了一类具有Allee效应和状态控制的捕食–食饵系统,建立了系统半平凡周期解的存在性和稳定性判据,并探讨了系统解的存在性、唯一性、稳定性和周期性等动力学性质。同时,对系统的相关动力学行为进行数值模拟,验证理论结果的有效性。
关键词 :捕食–食饵系统,Allee效应,状态控制,周期解

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,捕食动力系统在种群动力学研究中扮演重要角色,研究人员利用生态捕食系统来描述种群之间相互作用的动力学关系。捕食系统早期的研究内容主要是生物种群的持续生存问题,研究的一般方法为对所建立的生态数学模型稳定点的存在性和稳定性进行分析,进而判断该种群是否能持久生存,近些年该领域取得一些重要成果,其相关理论也日趋完善 [1] [2] [3] [4] 。Luo [5] 研究了水域温度的周期相变对生态系统内部特征的影响。文章指出温度随季节变化而具有一定的时间周期,温度的周期变化会导致种群的内禀增长率和环境最大承载量发生变化,进而影响系统的动力学行为,所得结论是比较符合自然界规律的。
在捕食–食饵系统中,两种群的捕食-食饵系统是比较常见的,然而,比较符合自然界种群增长规律的 Allee效应也受到很多关注,其被广泛应用到生态数学建模中 [6] [7] [8] [9] [10] 。Allee效应是以生态学家Allee的名字命名 [9] ,它描述了人口密度与人均增长率之间的正相关关系。论文 [11] 研究了具有Allee效应的Leslie-Gower捕食模型对猎物的复杂动力学,分析了在Allee效应下系统平衡点的存在性条件,证明了该模型具有Hopf分支的参数子集的存在性,最有趣的发现之一是Allee效应会增加生态灭绝的风险。论文 [12] 揭示了具有强Allee效应的捕食–食饵模型的分支行为,揭示了点对点异宿环的存在性,讨论了参数空间中延拓的数值技巧。论文 [13] 研究了一类具有Allee效应的离散捕食–食饵模型,研究结果表明Allee效应对捕食者和食饵的种群数量的影响,猎物和捕食者只能在一定数量范围内生长和共存。
近年来,许多学者在研究微分方程理论时都会考虑脉冲带来的影响作用 [14] [15] [16] 。实际上,状态脉冲微分方程广泛的应用于许多领域,且人类对自然资源的管理与开发都是离散的,而且还是瞬时完成的,从而在瞬时时刻也破坏了原有生态种群的固有状态,因此把这种瞬间扰动用脉冲微分方程来表示更加契合实际 [17] [18] [19] [20] [21] 。在论文 [22] 中,作者构建了基于比例依赖和状态脉冲反馈控制的Leslie捕食者–被捕食系统,并利用后继函数得到了系统阶-1周期解的存在性与唯一性以及轨道稳定性。在论文 [23] 中,作者研究了一类具有状态脉冲效应的捕食–食饵系统在不同阈值下释放天敌和喷洒农药的动态行为,利用Poincaré映射和Lambert W函数的性质,证明了半平凡解和正周期解存在性和稳定性。在论文 [24] 中,作者研究了具有脉冲状态反馈控制的捕食–食饵模型的动力学行为,利用Poincaré映射和类Poincaré准则得到了半平凡解和正阶-1周期解存在和稳定的充分条件。此外,利用Poincaré映射得到了周期解的分支图,并证明了混沌现象是通过一系列倍周期分岔产生的。
基于以上讨论结果,本论文构建一类具有Allee效应与状态控制的捕食–食饵动力系统,具体如下:
(1)
其中X和Y分别代表食饵和捕食者的种群密度,
代表着内禀增长率,
则代表环境最大容纳量,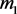 表示Allee阈值,
代表捕食者的死亡率,
为捕食率,
为转化率。
代表了在食饵达到阈值
时,食饵的捕获率。
表示Allee阈值,
代表捕食者的死亡率,
为捕食率,
为转化率。
代表了在食饵达到阈值
时,食饵的捕获率。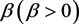 表示幼年捕食者的释放参数,
表示成年捕食者的释放参数。并且
,
。当食饵量达到临界阈值H时,采用一种控制策略,那么食饵和捕食者的数量分别为
和
。
表示幼年捕食者的释放参数,
表示成年捕食者的释放参数。并且
,
。当食饵量达到临界阈值H时,采用一种控制策略,那么食饵和捕食者的数量分别为
和
。
令
, , ,
, , ,
则模型(1)可以变为:
(2)
2. Poincaré映射及其预备知识
在系统(2)不具有脉冲效应下,它的动态行为可以解释如下:该系统有三个边界平衡和一个正平衡 ,并且 。通过计算,知道 和 均为系统(2)的鞍点,而当 时 是一个稳定的正结点,同时 也是一个稳定的正结点。
在这篇论文中,假设 和 总是成立的。基于系统(2)的生物学背景,那么只含有非负分量的解,并且在区域 内是连续可微的。
设 ,令 为系统(2)的任意解。当 时,通过点 的正向轨道定义为
(3)
定义2.1 (见 [25] ):如果存在一个正整数 使得k是满足 的最小正整数,那么系统(3)的轨线 被称为阶-k周期。
下一步是构造Poincaré映射。为了讨论系统(3)的动力学行为,首先考虑它的向量场。定义 为相集和 为脉冲集,假设 ,选取相集N和脉冲集M作为Poincaré截面,那么垂直等倾线 与相集N和脉冲集M分别相交于点 和点 ,与直线 相交于点 与点 。令 , 。显然,对任意点 ,都有 , ,而当 ,有 。另外,在 处,有 ,在 的左侧, ,并且在 的右侧 ,对任意点 作为初始点的轨线都将有 成立。
首先把截面N作为Poincaré截面。假设点 位于截面N上。由系统(2)的向量场性质可知,以点 为初始点的轨线与截面M交于点 ,其中 的值取决于 的值。如果用式子 来表示,那么在脉冲作用下点 映射到截面N上的一点 ,可以得到以下的Poincaré映射P:
(4)
接下来也介绍了另一种类型的Poincaré映射。选取截面M作为另一个Poincaré截面。假设点 位于截面M上,在脉冲作用下点 映射到截面N上的一点 ,以点 为初始点的轨线与截面M交于点 ,其中 的值取决于 以及参数 和 的值。就可以得到另一个的Poincaré映射 :
(5)
接下来,将考虑具有脉冲效应的自治系统:
(6)
其中 和 是连续微分方程, 是足够光滑并且梯度不等于零的函数,令 为系统(6)的一个正T周期解。接下来将介绍引理2.2。
引理2.2 (见 [26] ):如果Floquet乘子 满足条件 ,且
(7)
其中:
(8)
P,Q, , , , , , 均表示函数在点 处的函数值,且 和 , 代表第k次发生脉冲作用的时间,那么 是轨道渐进稳定的。
引理2.3 (见 [27] ):设 是 上的单参数族映射,并且满足下面的条件:
1)
2)
3)
4)
则映射F在 附近发生跨临界分岔,对所有的 来说,第一个分支为 。第二个分叉分支 的值随着 的增加而由负变正。当 时,第一个分支的不动点是稳定的;当 时,它是不稳定的,而分叉分支具有相反的稳定性。
3. 数学推导与分析
下面将分成 和 来讨论系统周期解的情况。首先,讨论了在 情况下半平凡周期解的存在性和稳定性,以及附近的分支行为。
3.1. 情况
很容易看出当且仅当 时系统(2)的半平凡周期解存在。因此,可以通过令 来开始研究。
定理3.1:系统(2)存在周期为T的半平凡周期解,其中
证明:当 ,系统(2)变为如下形式:
(9)
令 对于任意的 ;则从系统(9)变为(10),
(10)
令 ,系统(10)的解为 ,其中 是方程 的解。
令 ,则 ,因此,系统(9)有如下的半平凡周期解:
(11)
其中 , ,把半平凡周期解记为 。
现在讨论这个半平凡周期解的稳定性,利用引理2.2,可以得到关于系统(9)半平凡周期解的存在性和稳定性。
定理3.2:半平凡周期解(11)称为轨道渐近稳定的,如果它满足
(12)
且
证明:令
,
, ,
,
借助于引理2.2,通过计算得到
,
, , , , ,
(13)
此外有,
,(14)
其中
,
因此,得到Floquet乘子 如下所示:
(15)
其中
因此,当且仅当(12)成立时,有 成立。证毕。
注3.3:令 ,当 时,有 ,此时系统可能会发生分岔。因此,当 时,系统(2)可能会出现一个正周期解。因此,接下来讨论系统的分支情况。
首先,在 时,考Poincaré映射(4),令 且 ,u是一个充分小的非负数。这个映射就可以写成如下形式
(16)
其中,函数 是依赖于u和 的连续可微函数,且 ,则 。
其次,为了讨论映射(16)的分岔,利用引理2.3,得到以下定理。
定理3.4:当 , , 时,系统(2)发生跨临界分支,当参数 由 变化到 时,系统出现了一个正不动点。相应的,当 时,系统(9)有一个稳定的正周期解,其中 。
证明:首先,需要计算出在 处, 和 的值,其中 , 。
令
(17)
其中:
(18)
令 为系统(17)的任意一条轨线,且 , , ,则有
, , (19)
由表达式(19),可得
(20)
和
(21)
显然,可以推断出 ,且
(22)
因此,可以得到
其中:
,
由假设可知,在区域 上有 。因此,
可以确定
,
由此可得,
(23)
接下来,验证上述条件是否满足引理2.3。
1) 很容易去证实
, (24)
2) 运用表达式(22),
(25)
进而得到
这表明了 为对应于映射(16)的特征值1的不动点。
3) 如果(22)成立
(26)
4) 最后,不等式(23)表明
(27)
显然,上述所有条件都满足引理2.3的要求,因此定理3.4成立。
3.2. 情况
当 时,讨论了周期解的存在性和稳定性。根据系统(2)矢量场的性质,当 时,从 出发的轨线可能与脉冲集M相交无限次,且 , 。
当 时,从 出发的轨线可能与脉冲集M相交有限次,并且最终趋向于平衡点 ,其中, 。因此,接下来分为两种情况进行讨论:(A): ,(B): 。
3.2.1. 情况(A)
定理3.5:当 时,存在一个 , ,使得
此时,系统(2)存在一个正的阶-1周期解。其中,
证明:取相集N上的一点 ,且 是一个充分小的整的常数。从初始点 出发的轨线与脉冲集M相交于点 。在脉冲集M上,轨线受到脉冲作用的影响,与相集N相交于点 。而以 为初始点的轨线与脉冲集M相交于点 。如果 是充分小的,那么 ,则点 位于 的上方,也就是说 。由映射(5)可知 ,进而得到
(28)
垂直等斜线 与相集N交于点 ,以A为初始点的轨线与M交于点 ,则 ,经过脉冲作用跳跃到相集N上的点 处。经过分析,存在一个 , 使得 。此时点 重合于点A,系统(2)存在一个正的阶-1周期解。
当 ,点 位于A之上。由轨线的不相交性可知,经过点 的轨线最终将趋于 ,则系统不存在周期解。当 时,点 位于点A的下方。由轨线的不相交性可知,从初始点 出发的轨线与脉冲集M交与点 ,并且点 位于点U的下方。即 ,则
(29)
由不等式(28)和(29)可知,映射(5)有一个不动点,即系统(2)存在一个正的阶-1周期解。
定理3.6:当 时,设 为系统(2)的一个正阶-1周期解,并且该周期解的初始值为 ,其中 。如果条件
(30)
成立,其中
(31)
那么 为系统(2)的一个正阶-1周期解,并且该周期解是轨道渐近稳定的,具有渐近相位性质。
证明:基于定理3.5的结论,只需证明系统(2)的正阶-1周期解 的稳定性。在下面的讨论中,假设以周期T为周期的周期解过点 和点 ,其中由于系统(2)的向量场的性质而 成立。由于不知道周期T的表达形式,所以用引理2.2讨论这个正周期解的稳定性。这种定理的证明与定理3.1的区别在于
, (32)
而其它的则是一样的,因此
(33)
(34)
令 ;则
(35)
若 ,即当
(36)
成立时,这个周期解是稳定的。
注3.7:由此可知,如果存在一个 ,使得当 时有 ,那么系统会发生褶皱分岔。如果发生褶皱分岔,则当 时系统(2)存在一个稳定的正阶-2周期解,且随着 的增加,系统(2)的阶-2周期解也可能失去稳定性。
3.2.2. 情况(B)
定理3.8:存在一个 ,使得当 时,系统(2)存在一个正阶-1或者阶-2周期解,并且该周期解是轨道渐近稳定的。另外,系统不存在阶k ( )周期解。
证明:假设一条轨线与脉冲集M相切于点 与相集N分别交于点 和点 ,其中 且 。根据轨道的不相交性,对任意属于线段 上的点 ,其中 ,系统(2)通过点 的轨线随着时间的增加而不会与脉冲集相交,最终趋于稳定的内平衡点 。也就是说,从脉冲集M上的点 出发的轨线最终会到达 。很明显,此时系统(2)没有周期解。因此,由于脉冲作用使系统轨线和脉冲集M相交无限次的充分条件是 ,其中 与阈值h有关的。
根据定理3.5可知,系统存在阶-1周期解的充分条件为 ,假设 的取值满足条件,另取任意两点 和 ,使得 。可知这两点经过脉冲作用与相集N的交点为 和 均位于点 的上方,然后从系统的向量场和轨道的不相交性出发,我们可以看到 与 的后继点 和 的关系为
。 (37)
对任意的 ,根据Poincar映射(5)可知 , 和 ,此时,该系统(2)的周期解的存在情况如下:
1) 若 ,系统(2)存在一个正阶-1周期解;
2) 若 ,在不失一般性的情况下,假设 。因此,若 ,系统(2)存在一个正阶-2周期解;
3) 若 且 ,则系统(2)存在一个正阶-k周期解。实际上,这是不可能的,下面我们分两种情况来证明。
①
从(37)中也可以看出, , 和 之间只有两种位置关系: 和 。
1)
如果 成立,那么我们可以得到 ,并且 也是成立的。进一步由(37)可知 ,即 。通过归纳可知
(38)
与1)类似有
2)
由(37),可知
(39)
②
从(37)中也可以看出, , 和 之间只有两种位置关系: 和 。
1)
若 ,我们可知 ,进而得出 。由(37) 可知, 。以此类推,可知
(40)
与1)类似有
2)
由(37),可知
(41)
如果系统(2)存在阶-k 周期解,则 , ,这与(38)-(41)是矛盾的。因此,在系统(2)中没有阶k 周期解。事实上,存在稳定的阶-1或者阶-2周期解。由(39)可知 且 ,其中 。因此 且 。所以系统(2)在 的情况下存在一个稳定的阶-2周期解。类似的,可以得到系统(2)在 与 的情况下存在一个稳定的阶-1周期解,并且在 的情况下有一个稳定的阶-2周期解。
由此可知,在 这种情况下,系统(2)只存在稳定的阶-1周期解和阶-2周期解。
4. 数值模拟
假设参数值是 , , , ,并且可以得到 。此时系统(2)有一个
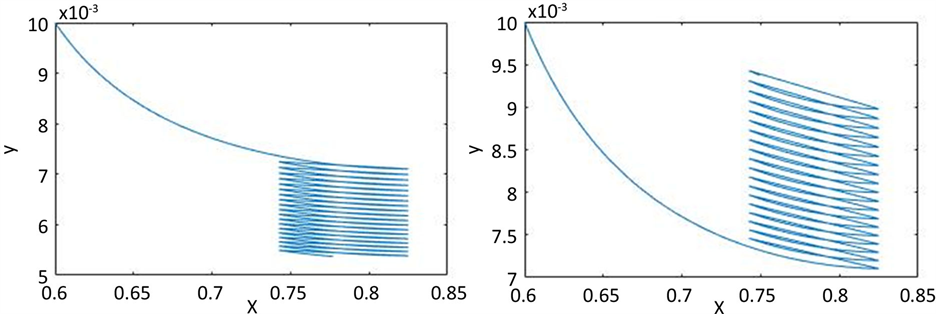
内平衡点 ,其中 , 且有 ,则平衡点 是稳定的结点。由定理3.1可知,当 时,系统(2)存在一个半平凡周期解,并且当定理3.3的条件成立时,这个半平凡周期解是稳定的。从注3.3,可以看出在 , 时,可以计算出 。令 ,则半平凡周期解是渐近稳定的。以 为初始值的解随着时间的增加将会趋向于半平凡周期解,如图1(a)所示。令 ,则由图1(b)可知半平凡周期解是不稳定的。
由定理3.4中可知,当 , 时,系统发生跨临界分岔,半平凡周期解通过跨临界分岔产生稳定的阶-1周期解。已知 ,保持初始点 不变,令 ,然后系统(2)通过跨临界分岔产生稳定的阶-1周期解,如图2所示。
由定理3.5中可知,当 时,系统不存在半平凡周期解,当h满足 且定理3.4的条件成立时,系统(2)有一个正阶-1周期解,如图3(a),当定理3.6的条件满足时,周期解是轨道渐近稳定的,如图3(b)。
从注3.7中可以看出,当 和 时,系统可能有关于参数 的褶皱分支,增大参数 的值,
 (a) (b)
(a) (b)
Figure 1. Trajectories with the initial point (0.6, 0.01) of system (2) with α = 0.1, h = 0.825, (a) β = 0.02, (b) β = 0.05
图1. 当α = 0.1,h = 0.825时,系统(2)以(0.6, 0.01)为初始点的轨线,(a) β = 0.02,(b) β = 0.05
 (a) (b)
(a) (b)
Figure 2. When τ = 0, (a) The existence of positive order-1 periodic solution, (b) The stability of positive order-1 periodic solution, where α = 0.1, h = 0.825, β = 0.13
图2. 当τ = 0时,(a) 系统(2)正的阶-1周期解的存在性,(b) 系统(2)正的阶-1周期解的稳定性,其中α = 0.1,h = 0.825,β = 0.13
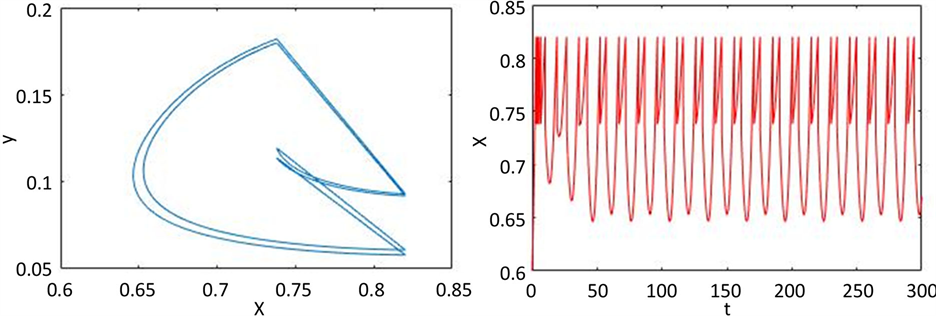
令 ,保持其它参数的取值不变,可以看出系统出现了一个正阶-2周期解,且该周期解是稳定的,如图4。当参数 的取值持续增大时,发生了一个倍周期分岔。令 ,可以观察到系统产生了一个阶-4周期解,从它的x的时序图中可以看出该周期解是稳定的,如图5所示。由定理3.8可知,当 且 时,当定理3.8的条件成立时,系统(2)仅存在稳定的阶-1周期解(如图6(a),图6(b))和阶-2周期解(如图6(c),图6(d))。分别展示了系统(2)的稳定的阶-1周期解和阶-2周期解及其相对应的x的时序图。由时序图可以看到周期解是轨道渐近稳定的。
5. 结论
本论文主要构建了一类具有Allee效应与状态控制的捕食-食饵动力系统,研究了半平凡周期解的存在性和稳定性,阶-1周期解、阶-2周期解和阶-k周期解的存在性和稳定性,以及唯一性和周期性,得到了半平凡周期解和正阶-1周期解存在和稳定的充分条件。从数值模拟可以看出,如果把 作为系统动力
 (a) (b)
(a) (b)
Figure 3. When τ > 0 and h < x*, (a) The existence of positive order-1 periodic solution, (b) The stability of positive order-1 periodic solution, where α = 0.1, h = 0.82, β = 0.11, τ = 0.001
图3. 当τ > 0且h < x*时,(a) 系统(2)正的阶-1周期解的存在性,(b) 系统(2)正的阶-1周期解的稳定性,其中α = 0.1,h = 0.82,β = 0.11,τ = 0.001
 (a) (b)
(a) (b)
Figure 4. When τ > 0 and h < x*, (a) The existence of positive order-2 periodic solution, (b) The stability of positive order-2 periodic solution, where α = 0.1, h = 0.82, β = 0.81, τ = 0.001
图4. 当τ > 0且h < x*时,(a) 系统(2)正的阶-2周期解的存在性,(b) 系统(2)正的阶-2周期解的稳定性,其中α = 0.1,h = 0.82,β = 0.81,τ = 0.001
 (a) (b)
(a) (b)
Figure 5. When τ > 0 and h < x*, (a) The existence of positive order-4 periodic solution, (b) The time-series of x, where α = 0.1, h = 0.82, β = 0.945, τ = 0.001
图5. 当τ > 0且h < x*时,(a) 系统(2)正阶4周期解的存在性,(b) x的时序图,其中α = 0.1,h = 0.82,β = 0.945,τ = 0.001
 (a) (b)
(a) (b) (c) (d)
(c) (d)
Figure 6. When τ > 0, h > x* > (1 − α)h, (a) The existence of positive order-1 periodic solution; (b) The time-series of x; (c) The existence of positive order-2 periodic solution; (d) The time-series of x, where α = 0.1, h = 0.84, , τ = 0.001, (a)-(b) β = 0.105; (c)-(d) β = 0.8
图6. 当τ > 0且h > x* > (1 − α)h时,(a) 系统(2)正阶-1周期解的存在性,(b) x的时序图,(c) 系统(2)正阶-2周期解的存在性,(d) x的时序图,其中α = 0.1,h = 0.84,τ = 0.001,(a)-(b) β = 0.105;(c)-(d) β = 0.8
学分析的关键因素,当 时,随着 的增加,系统中的阶-1周期解逐渐变为正阶-2周期解和正阶-k周期解;当 时,系统中存在正阶-1阶周期解和阶-2周期解。总体来说,模拟结果验证了理论推导结果的有效性。
基金项目
国家自然科学基金面上项目(31570364)。
文章引用
马凯丽. 具有Allee效应和状态控制的捕食–食饵系统的动力学分析
Dynamic Analysis of Predator-Prey System with Allee Effect and State Control[J]. 应用数学进展, 2018, 07(07): 918-933. https://doi.org/10.12677/AAM.2018.77109
参考文献
- 1. Legović, T. and Cruzado, A. (1997) A Model of Phytoplankton Growth on Multiple Nutrients Based on the Michaelis-Menten-Monod Uptake, Droop’s Growth and Liebig’s Law. Ecological Modelling, 99, 19-31. https://doi.org/10.1016/S0304-3800(96)01919-9
- 2. Busenberg, S., Kumar, S.K., Austin, P. and Wake, G. (1990) The Dy-namics of a Model of a Plankton-Nutrient Interaction. Bulletin of Mathematical Biology, 52, 677-696. https://doi.org/10.1007/BF02462105
- 3. Jang, S.J. and Baglama, J. (2005) Nutrient-Plankton Models with Nutrient Recycling. Computers & Mathematics with Applications, 49, 375-387. https://doi.org/10.1016/j.camwa.2004.03.013
- 4. Freund, J.A., Mieruch, S., Scholze, B., Wiltshire, K. and Feudel, U. (2006) Bloom Dynamics in a Seasonally Forced Phytoplankton-Zooplankton Model: Trigger Mechanisms and Timing Effects. Ecological Complexity, 3, 129-139. https://doi.org/10.1016/j.ecocom.2005.11.001
- 5. Luo, J. (2013) Phytoplankton-Zooplankton Dynamics in Periodic Environ-ments Taking into Account Eutrophication. Mathematical Biosciences, 245, 126-136. https://doi.org/10.1016/j.mbs.2013.06.002
- 6. Berec, L., Angulo, E. and Courchamp, F. (2007) Multiple Allee Effects and Population Management. Trends in Ecology & Evolution, 22, 185-191. https://doi.org/10.1016/j.tree.2006.12.002
- 7. Courchamp, F., Clutton-Brock, T. and Grenfell, B. (1999) Inverse Density De-pendence and the Allee Effect. Trends in Ecology & Evolution, 14, 405-410. https://doi.org/10.1016/S0169-5347(99)01683-3
- 8. Guo, H., Chen, L. and Song, X. (2010) Mathematical Models of Restora-tion and Control of a Single Species with Allee Effect. Applied Mathematical Modelling, 34, 3264-3272. https://doi.org/10.1016/j.apm.2010.02.018
- 9. Allee, W.C., Animal Aggregations (1931) A Study in General Sociology. Uni-versity of Chicago Press.
- 10. Groom, M.J. (1998) Allee Effects Limit Population Viability of an Annual Plant. The American Na-turalist, 151, 487-496. https://doi.org/10.1086/286135
- 11. Cai, Y., Zhao, C., Wang, W. and Wang, J. (2015) Dynamics of a Leslie-Gower Predator-Prey Model with Additive Allee Effect. Applied Mathematical Modelling, 39, 2092-2106. https://doi.org/10.1016/j.apm.2014.09.038
- 12. Van Voorn, G.A., Hemerik, L., Boer, M.P. and Kooi, B.W. (2007) Heteroclinic Orbits Indicate Overexploitation in Predator-Prey Systems with a Strong Allee Effect. Mathematical Biosciences, 209, 451-469. https://doi.org/10.1016/j.mbs.2007.02.006
- 13. Cheng, L. and Cao, H. (2016) Bifurcation Analysis of a Discrete-Time Ra-tio-Dependent Predator-Prey Model with Allee Effect. Communications in Nonlinear Science and Numerical Simulation, 38, 288-302. https://doi.org/10.1016/j.cnsns.2016.02.038
- 14. Yu, H., Zhong, S., Agarwal, R.P. and Sen, S.K. (2011) Three-Species Food Web Model with Impulsive Control Strategy and Chaos. Communications in Nonlinear Science and Numerical Simulation, 16, 1002-1013. https://doi.org/10.1016/j.cnsns.2010.05.014
- 15. Baek, H. (2010) Dynamic Complexities of a Three-Species Bedding-ton-DeAngelis System with Impulsive Control Strategy. Acta Applicandae Mathematicae, 110, 23-38. https://doi.org/10.1007/s10440-008-9378-0
- 16. Liu, X. and Chen, L. (2003) Complex Dynamics of Holling Type II Lotka-Volterra Predator-Prey System with Impulsive Perturbations on the Predator. Chaos, Solitons & Fractals, 16, 311-320. https://doi.org/10.1016/S0960-0779(02)00408-3
- 17. Gong, W.Z., Zhang, Q. and Tang, X.H. (2012) Existence of Subharmonic Solutions for a Class of Second-Order p-Laplacian Systems with Impulsive Effects. Applications of Mathematics, 59, 543-570.
- 18. Liu, Z., Zhong, S., Yin, C. and Chen, W. (2011) On the Dynamics of an Impulsive Reaction-Diffusion Predator-Prey System with Ratio-Dependent Functional Response. Acta Applicandae Mathematicae, 115, 329. https://doi.org/10.1007/s10440-011-9624-8
- 19. Yu, H., Zhong, S., Ye, M. and Chen, W. (2009) Mathematical and Dynamic Analysis of an Ecological Model with an Impulsive Control Strategy and Distributed Time Delay. Mathematical and Computer Modelling, 50, 1622-1635. https://doi.org/10.1016/j.mcm.2009.10.008
- 20. Hui, J. and Chen, L.S. (2005) A Single Species Model with Impulsive Diffusion. Acta Mathematicae Applicatae Sinica, 21, 43-48. https://doi.org/10.1007/s10255-005-0213-3
- 21. Yu, H., Zhong, S. and Ye, M. (2009) Dynamic Analysis of an Ecological Model with Impulsive Control Strategy and Distributed Time Delay. Mathematics and Computers in Simulation, 80, 619-632. https://doi.org/10.1016/j.matcom.2009.09.013
- 22. Liang, Z., Zeng, X., Pang, G. and Liang, Y. (2017) Periodic Solution of a Leslie Predator-Prey System with Ratio-Dependent and State Impulsive Feedback Control. Nonlinear Dynamics, 89, 2941-2955. https://doi.org/10.1007/s11071-017-3637-4
- 23. Nie, L., Teng, Z., Hu, L. and Peng, J. (2009) Existence and Stability of Periodic Solution of a Predator-Prey Model with State-Dependent Impulsive Effects. Mathematics and Computers in Simulation, 79, 2122-2134. https://doi.org/10.1016/j.matcom.2008.11.015
- 24. Jiang, G. and Lu, Q. (2007) Impulsive State Feedback Control of a Preda-tor-Prey Model. Journal of Computational and Applied Mathematics, 200, 193-207. https://doi.org/10.1016/j.cam.2005.12.013
- 25. Dai, C., Zhao, M. and Chen, L. (2012) Dynamic Complexity of an Ivlev-Type Prey-Predator System with Impulsive State Feedback Control. Journal of Applied Mathematics, 2012, Article ID: 534276. https://doi.org/10.1155/2012/534276
- 26. Simeonov, P.S. and Bainov, D.D. (1988) Orbital Stability of Periodic Solutions of Autonomous Systems with Impulse Effect. International Journal of Systems Science, 19, 2561-2585. https://doi.org/10.1080/00207728808547133
- 27. Rasband, S.N. (2015) Chaotic Dynamics of Nonlinear Systems. Courier Dover Publications, New York.