ABSTRACT

We use the ghost fluid method to deal with the moving boundary one-dimensional compressible multi-material flows problem on ALE schemes. The grids at the boundary move along the boundary to keep track the moving boundary while the inner grids are adjusted continuously to improve the over-all grid quality. Trace the material interface using Level set equation on ALE schemes. Transform the multi-material flows problem into single-medium problems to avoid non-physical oscillations near the material interface through ghost fluid.

Keywords:ALE, Ghost Fuid Method, Moving Boundary

ALE框架下虚拟流体方法模拟移动边界的 一维可压缩多介质流动问题

刘晓慧¹，李 肖²

¹北京计算科学研究中心，北京

²中国工程物理研究院研究生院，北京

收稿日期：2018年11月24日；录用日期：2018年12月20日；发布日期：2018年12月27日

摘 要

在ALE框架下采用Ghost Fluid方法处理移动边界的一维可压缩多介质流动问题。在边界处网格跟随边界移动从而可以追踪物质边界，内部网格不断调整从而改善整体网格质量。使用ALE框架下Level Set方程追踪物质界面。利用虚拟流体把多介质问题转化为多个单介质问题，避免物质界面附近非物理振荡。

关键词 :ALE，Ghost Fluid方法，移动边界

Copyright © 2018 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

随着科技的发展，可压缩多介质流动的数值模拟受到越来越多的关注，在流体力学、航空航天以及核物理等领域都有着重要的理论和实际应用背景，例如气液耦合问题、流固耦合问题、炸弹爆炸、激波碰撞物质界面等，都属于可压缩多介质流动的范畴。移动边界问题在生活和工程中也经常碰到，例如液体流动、冰川融化、石油开采、河床勘测等都会涉及到，如何追踪边界面演化也给数值模拟带来了很大的挑战。

移动边界的可压缩多介质流动问题，不仅由于边界移动带来的计算区域改变，同时可能伴有强激波、界面大变形等问题，因此采用传统的欧氏方法和拉氏方法进行计算遇到了较大的问题和困难 [1] 。拉氏方法可以很好的追踪移动边界和物质界面，同时由于物质界面清晰，不会出现混合单元，从而避免了由于密度污染和状态方程的混合带来的非物理振荡。但是拉氏方法由于网格跟随流体和边界移动，当边界或者物质界面出现大变形时，就会受到网格严重变形扭曲的困扰，甚至导致算死。传统的单介质欧氏方法很好的解决了大变形的问题，但是混合单元的计算会带来另一个很大的问题，不同介质和状态方程的混合会导致在物质界面附近出现非物理振荡，此外由于边界条件被安排在控制方程中，而导致边界信息模糊也给计算带来了很多问题 [1] 。

欧氏方法下的Ghost Fluid方法 [2] ，采用Lev Set方程追踪物质界面，通过虚拟流体将多介质问题转化为多个单介质问题，不仅解决了物质界面大变形带来的困扰，同时处理了混合单元的问题，避免了非物理振荡。但是它在处理移动边界问题时由于计算区域固定，但是真实流体的区域在改变，会导致存在很多空网格，这些空网格需要特殊处理，不仅带来了计算量，同时也会模糊物质边界。

ALE方法是由Hirt [3] 等首先提出。ALE方法具有任意网格移动速度，具有良好的灵活性和适用性，可以处理复杂边界和移动边界的问题。良好的网格移动策略，既可以避免大变形带来的网格严重扭曲变形问题。

本文在ALE框架下采用Ghost Fluid方法处理移动边界的可压缩多介质流动问题。这样对于边界可以采用网格追踪，从而解决了欧氏框架下空网格和边界模糊的问题。本文主要内容如下，2.1和2.2给出了一维Euler方程和ALE框架下离散格式；2.3和2.4介绍了Level Set方程和Ghost Fluid方法；3介绍了移动边界并且给出了一种网格移动策略。接下来数值算例和结论。

2. 理论方法

2.1. 控制方程

一维无粘可压缩Euler方程组为 [4] ：

$\frac{\partial U}{\partial t}+\frac{\partial F\left(U\right)}{\partial x}=0,$ (2.1)

其中守恒量U和通量F分别是：

$U=\left[\begin{array}{c}\rho \\ \rho u\\ \rho E\end{array}\right],F\left(U\right)=\left[\begin{array}{c}\rho u\\ \rho u^2+p\\ \rho Eu+pu\end{array}\right],$

其中 $\rho ,u,p$ 分别表示密度、x方向上的速度和压强。E表示质量比总能，其表达式为：

$E=e+\frac{u^2}{2}$ (2.2)

其中e是质量比内能。为了封闭方程组，还需要给出状态方程(EOS)，不同的物质对应不同的状态方程，这里我们使用理想气体的状态方程：

$p=\left(\gamma -1\right)\rho e$

其中γ是比热比，是一个对于不同气体取不同值的无量纲常数。

2.2. ALE方法数值离散

采用基于有限体积格式的Godunov型ALE方法，用于求解可压缩多介质流动问题。对于二维Euler方程组在一个控制单元上的积分形式为：

${\displaystyle {\int }_{\Omega \left(t\right)}\frac{\partial U}{\partial t}\text{d}V}+{\displaystyle {\int }_{\Omega \left(t\right)}\left(\frac{\partial F}{\partial x}+\frac{\partial G}{\partial y}\right)\text{d}V}=0.$ (2.3)

其中 $\Omega \left(t\right)$ 是一个移动的控制单元。利用Green公式和雷诺输运定理，上述积分形式可以变形为 [5] ：

$\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{\Omega \left(t\right)}U\text{d}V}+{\displaystyle {\int }_{\partial \Omega \left(t\right)}\left(\left(F,G\right)\cdot N-\left(w\cdot N\right)U\right)\text{d}l}=0.$ (2.4)

其中 $\partial \Omega \left(t\right)$ 和w是控制单元 $$ 的边界和移动速度，N是边界的外法向量。如果 $w=0$ 就是欧氏方法，w取流体速度就是拉氏方法。

接下来，我们将上述积分退化到一维问题，在一维Euler方程组上对于上述ALE积分进行离散。在离散之前先做一些记号的解释。这里用上角标n表示时间层 $t^n$ ，下角标表示空间位置。用 $I^n$ 代表控制单元 $\left[x_{i-1/2},x_{i+1/2}\right]$ 它的区间长度使用 $\Delta x^n$ 表示。

在控制单元 $I^n$ 上使用Godunov方法，时间上采用一阶向前欧拉格式，上述积分方程在一维情况下的离散格式为：

$U_i^{n+1}=\frac{\Delta x_i^n}{\Delta x_i^{n+1}}{U}_i^n-\frac{\Delta t}{\Delta x_i^{n+1}}\left(F_{i+\frac{1}{2}}-F_{i-\frac{1}{2}}+w_{i-\frac{1}{2}}{U}_{i-\frac{1}{2}}-w_{i+\frac{1}{2}}{U}_{i+\frac{1}{2}}\right)$ (2.5)

其中 $U_i^n$ 在控制单元 $I^n$ 上的积分平均值， $\Delta t=t^n+1-t^n$ 代表时间步长， $w_{i-1/2}$ 和 $w_{i+1/2}$ 表示单元节点 $x_{i-1/2}$ 和 $x_{i+1/2}$ 的移动速度。 $$ 和 $F_{i+1/2}-w_{i+1/2}{U}_{i+1/2}$ 是代表单元节点处的数值通量，有很多种方法可以得到它们，最常用的方法是求解一个黎曼问题。

这里我们以 $F_{i+1/2}-w_{i+1/2}{U}_{i+1/2}$ 为例，给出对应的黎曼问题如下：

$\begin{array}{l}{U}_t+F_x=0,\hfill \\ IVS:U\left(x,0\right)=\{\begin{array}{l}{U}_L=U_i^n,x<0,\\ U_R=U_{i+1}^n,x>0.\end{array}\hfill \end{array}$ (2.6)

对应的数值通量表达式为：

$F_{i+\frac{1}{2}}-w_{i+\frac{1}{2}}{U}_{i+\frac{1}{2}}=F^{w_{i+\frac{1}{2}}}-w_{i+\frac{1}{2}}{U}^{w_{i+\frac{1}{2}}}$ (2.7)

其中 $U^{w_{i+1/2}}$ 和 $F^{w_{i-1/2}}$ 分别表示沿着 $\frac{x}{t}=w_{i+1/2}$ 方向的守恒量和通量值。

2.3. Level Set方程

利用拉氏方法处理多介质流动问题时，可以清晰的分辨物质界面，然而这种方法难以处理网格大变形问题。本文采用ALE方法，在计算中可根据需要不断地调整网格以保证较好的网格质量，有良好的灵活性和适应性，但是无法利用网格追踪物质界面。因此为了解决这个问题，本文引入Level Set方程，利用Level Set方程追踪物质界面。

二维情况下的Level Set方程如下：

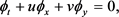(2.8)

其中 $\varphi$ 表示符号距离函数， $\varphi$ 的零值面表示物质界面， $\varphi$ 取负值时代表一种介质，取正值时代表另一种介质，每一种介质具有不同的状态方程。由于计算方法的内在效应，在计算一段时间之后， $\varphi$ 将不再满足符号距离函数的性质。因此需要对 $\varphi$ 进行初始化，使其仍然近似表示符号距离函数。本文采用如下的初始化方程进行初始化：

${\varphi }_t+S\left({\varphi }_0\right)\left(\sqrt{{\varphi }_x^2+{\varphi }_y^2}-1\right)=0$ (2.9)

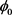其中 ${\varphi }_0$ 是初始化之前的 $\varphi$ 值， $S\left({\varphi }_0\right)$ 是符号。

对于一维问题只需要把所有y方向的值去掉即可。

2.4. Ghost Fluid方法

对于单介质问题守恒型的欧氏方法非常有效，并且可以很好的解决大变形问题。但是当处理多介质流体流动问题时，经常会由于密度污染和状态方程的巨大改变在物质界面附近出现一些非物理震荡。拉氏方法可以很好的解决物质界面处非物理震荡问题，但是在碰到大变形问题时，经常会由于网格严重变形而导致算死。

Ghost Fluid方法很好的结合了上述两种方法的优点，利用Level Set追踪物质界面，然后通过虚拟流体，将一个多介质问题转化为多个单介质问题，再通过求解单介质的方法来分别求解每种流体，这样可以成功避开界面两侧流体由于状态方程不同而带来的振荡问题。同时本文采用ALE方法，不断地调整网格质量，从而避免了网格严重变形的问题。虚拟流体的具体实施过程参考 [2] ，如图1。

图1. 虚拟流体

3. 移动边界和网格移动速度

处理移动边界问题的数值方法可以分为两大类：拉氏方法和欧氏方法。拉氏方法可以显示追踪边界演化，但是经常遭受大变形的困扰。欧氏方法的边界条件被安排在控制方程中，导致边界信息模糊。

本文采用ALE方法处理移动边界的多介质流动问题，在边界处网格跟随边界一起移动，内部网格重新给出新的移动策略，从而可以调整网格质量，这样既可以显示追踪移动边界，又可以避免大变形问题带来的困难。同时利用Level Set方法追踪多介质的物质界面，借助虚拟流体把多介质问题转换为多个单介质问题，避免了由于密度污染和状态方程的混合带来的非物理振荡。

图2. 带移动活塞的激波管问题

本文考虑一维激波管问题如图2，内部是多介质流，左端是一个固定壁或者无限长，右端是一个移动的活塞。活塞的移动速度记做 $u_{piston}\left(t\right)$ ，初始时刻计算区域记做 $\left[a,b\right]$ ，此时活塞位置 $x_{piston}^{old}=b$ ，对于该计算区域进行网格剖分，为了介绍方便，这里我们取均匀网格，网格步长为 $\Delta x=\left(b-a\right)/N$ ，其中N为网格数，如图3(a)。网格节点位置为：

$x_{i-\frac{1}{2}}^{old}=a+\Delta x\left(i-1\right),i=1,2,\cdots ,N+1$ (3.1)

经过一段时间 $\Delta t$ ，活塞位置为：

$x_{piston}^{new}=b+{\displaystyle {\int }_0^{\Delta t}{u}_{piston}\left(t\right)\text{d}t}$ (3.2)

然后我们给出新的网格节点位置为：

$x_{i-\frac{1}{2}}^{new}=a+\frac{x_{i-\frac{1}{2}}^{new}-x_{i-\frac{1}{2}}^{old}}{\Delta t},i=1,2,\cdots ,N+1$ (3.3)

对应的网格移动速度为：

$w_{i-\frac{1}{2}}=\frac{x_{i-\frac{1}{2}}^{new}-x_{i-\frac{1}{2}}^{old}}{\Delta t},i=1,2,\cdots ,N+1$ (3.4)

上述网格移动策略等价于经过一个时间步长之后，计算出新的计算区域，然后将新的计算区域重新均匀划分为N个网格，如图3(b)。这种网格移动方式，既可以很好的追踪移动边界位置，又可以保证网格质量。

图3. ALE框架下的新旧网格

4. 数值算例

这里我们考虑一个半无限长激波管，内部是两种介质，左端是一个移动的活塞。计算区域为 $\left[0,1\right]$ ，网格点数取为200，活塞移动速度取为-250，计算初值为：

$\{\begin{array}{l}\rho =1.0,u=0.75,p=1.0,\gamma =1.4,x<0.25,\\ \rho =0.125,u=0.0,p=0.1,\gamma =1.2,x>\mathrm{0.25.}\end{array}$ (4.1)

图4给出了t = 0.0015时刻的数值结果和精确解的密度比较。从图中可以看出在这种网格移动策略下，利用GFM方法可以很好的模拟一维移动边界下的多介质流动问题，并且在活塞边界和物质界面附近不会出现非物理震荡

图4. 数值解和精确解的密度对比图

5. 结论

本文基于一种网格移动策略，在ALE框架下利用虚拟流体方法数值模拟移动边界下的多介质流动问题。在移动边界附近网格移动速度等于边界移动速度，内部网格重新均匀划分，这样既避免了网格大变形，又可以很好的追踪移动边界。同时采用Level Set方程追踪物质界面，利用虚拟流体的方法将多介质问题转化为多个单介质问题，避免了物质界面处的非物理震荡。通过数值实验很好的验证了我们的结论。

文章引用

刘晓慧,李 肖. ALE框架下虚拟流体方法模拟移动边界的一维可压缩多介质流动问题
GFM for One-Dimensional Compressible Multi-Material Flows with Moving Boundary on ALE Frame[J]. 应用数学进展, 2018, 07(12): 1638-16440. https://doi.org/10.12677/AAM.2018.712191

参考文献