Advances in Applied Mathematics
Vol.
08
No.
05
(
2019
), Article ID:
30571
,
12
pages
10.12677/AAM.2019.85117
The Jones Polynomials of Class of Knots
Wei Zheng, Dongyu Geng, Luying Zhao*
Liaoning Normal University, Dalian Liaoning

Received: May 9th, 2019; accepted: May 24th, 2019; published: May 31st, 2019

ABSTRACT
Knot theory is a branch of mathematical topology and the classification of knots is a very important problem in the field of knots. People solve the problem of knot by looking for knot invariants. Knot invariants are trichrome, crossover number, knot number, bridge number, knot polynomial, knot group, etc. In this paper, we study a class of special Brunnian link. The formula for calculating the Jones polynomial of this kind of chain is given. In order to realize the calculation of
Jones polynomials, on the one hand, by calculating
and
bracket polynomials, the calculating formulas of
bracket polynomials are obtained. On the other hand, by dividing the given orientation into regions
, the enumeration method is used to find the calculation rule of the number of twists, and then the calculation formula of the number of twists
is given. Combining the above two aspects, the calculation formula of the Jones polynomial
is obtained. The innovation of this paper is to generalize the original definition of connected sum, to connect with a specific segment,
to construct
, then
to construct
, and then to find the
computational law, which greatly simplifies the computational process.
Keywords:Pretzel Knot, Jones Polynomial, Twist, Brunnian Link

一类链环的Jones多项式
郑玮,庚东雨,赵璐莹*
辽宁师范大学,辽宁 大连

收稿日期:2019年5月9日;录用日期:2019年5月24日;发布日期:2019年5月31日

摘 要
Jones多项式是纽结理论中重要的不变量之一。若两个链环投影图的Jones多项式的不同,则这两个投影图对应着不同的链环,这是研究纽结和链环分类问题的重要方法。Brunnian link是一类既特殊又简单的链环,本文研究一类特殊的Brunnian链
环,本论文给出了
的Jones多项式的计算公式。
关键词 :排叉结,琼斯多项式,拧数,Brunnian link
Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
纽结理论是数学中拓扑学的一个分支 [1] ,纽结的等价分类问题在纽结领域中十分重要 [2] 。人们通过寻找纽结不变量来解决纽结的等价问题,常见的纽结不变量有三色性、交叉数、解结数、桥数、纽结多项式、纽结群等。
本文研究了一类特殊的Brunnian链环
,并给出了这类链环的Jones多项式的计算公式。为实现
的多Jones项式的计算,一方面,通过计算
、 的尖括号多项式,逐步递推进而得到
尖括号多项式的计算公式。另一方面,通过对给定向的
进行区域划分,用枚举法找到拧数的计算规律,进而给出了
拧数的计算公式。结合以上两方面得出了
的Jones多项式的计算公式。
本文的创新之处在于对原有的连通和的定义进行推广,以特定的弧段去做连通,由
构造
,再由
构造
,进而可找到
的计算规律,从而大大简化了计算过程。
2. 预备知识
2.1. 纽结及投影图
把嵌入到三维欧式空间
中或者球面
中的单位圆周
称为纽结,设K是
中的简单闭曲线,且
,称K是一个纽结 [3] 。
若给定纽结一个方向便可得到一个定向纽结。
选择一个恰当的平面,将三维空间中的纽结正则投影到平面上,且满足:
①只有有限多个交叉点;
②每个交叉点都是二重点;
③在每个二重点处,上下两线的投影都是互相穿越交叉的则称为纽结投影图。注意,平面的选择不同随之投影图不唯一。
2.2. 链环
将若干互不相交的圆周
嵌入到三维欧式空间
中或者球面
中,由这些圆周形成的空间图形称为链环,记为
。其中
称为L的一个分支,n为

链环的分支数 [4] 。
若通过和痕后所有的
都是平凡纽结,则此时称L为平凡链环;若给定每个分支一个方向,便可得到一个定向链环。
2.3. Reidemeister Move (R变换)
Reidemeister变换是改变纽结的正则投影图的三种方式,每一种都会改变交叉点之间的关系 [1]
RI变换:
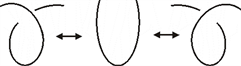
RII变换:

RIII变换:

纽结经过Reidemeister变换后纽结的拓扑性质不变,这是一个等价变换。虽然一个纽结有很多个投影图,但这些投影图之间是等价的。之后提到的有关纽结的投影图都指的是正则投影。一个投影图在等价意义下唯一确定一个纽结 [5] 。
2.4. 纽结连通和
设纽结
和
,各取一个走向,将其放在一个平面的两侧,分别把它们的一小段(哪一小段均可)拽向分隔平面,在平面处接通使走向协调,便得到两个有向纽结的和,又称为连通和,记作



2.5. 尖括号多项式
1) 介绍A通道、B通道:

对于上图的交叉点,其中,A通道:若由上行线到下行线逆时针旋转所经过的区域称为A通道,反之,B通道:若由上行线到下行线顺时针旋转所经过的区域称为B通道。
尖括号多项式满足如下的拆接关系:
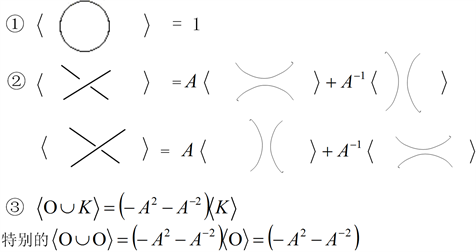
2.6. 拧数
对于一个链环L的有向投影图,称全体交叉点的的+1和−1的总和为L的拧数。对于每一个交叉点处,有从上行线的箭头转到下行线的箭头的最小转角是逆时针记为+1;从上行线的箭头转到下行线的箭头的最小转角是顺时针记为−1 [3] 。
2.7. Jones多项式
设
是
中的定向环链。因此,有Jones多项式
与之对应,且满足下列条件:
1)
是合痕不变量;
2)有拆接公式:
。
3)
。
在(2)式中
是三个只在一个交叉点不同的环链,也就是它们分别是正交叉点、负交叉点和保持定向的拆接。

2.8. 引理1
设
是一个排叉结如下图,当s为奇数时,
是一个纽结,当s为偶数时,
是一个两分支的链环,并且有
则 [4] :

2.9. 引理2
定义
是一个如下图的排叉结,含
个交叉点,由尖括号多项式的运算法则从最右面的交叉点开始打开可得
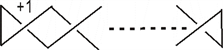

2.10. 引理3
定义具有
个半扭转的横向排列称为一个
。其中
表示
个横向半扭转 [6] 。

当
时表示正的半扭转,当
时表示负的半扭转。
如图所示。

当
时,此时
变成
。这时所有的半扭转消失,如图所示 [6] 。
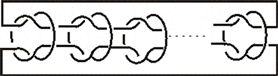
当
时,
变成
,是构成
的单位元素,也可以理解为由
加入
个半扭转得到的,如图所示。
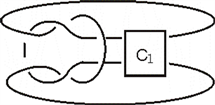
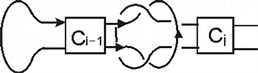
3. 定理证明
首先,将
如左图逆时针旋转90˚变为右图,右图可以看成两个排叉结
和
做连通和得到的 [2]
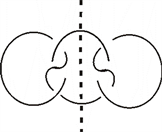
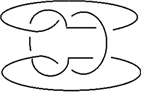
由引理,所以
,将
代入
的通项公式得到
在
上标记两段弧记为
,如图所示

按照尖括号多项式的运算法则将
的全部交叉点打开,从中选取带有弧
的平凡分支有两种情况,当弧
在同一分支时记为a如左图,当弧
在不同分支时记为b如右图

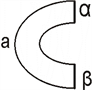
根据尖括号多项式的计算法则可知
可以写成
的线性组合,即
下面计算
可以看作
与
沿着
两段弧对应做连通和所得,如右图所示
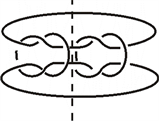

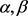
由尖括号多项式的运算法则可知,在计算
的过程中可先打开左侧
中的全部交叉点,所得的投影图有两种情况,a与
沿着弧
对应做连通和可得投影图如左图,根据RII变换最终可变成两分支的平凡链环,b与
沿着弧
对应做连通和,所得投影图为
,如右图


因此有
。
所以
。
同理
可看作
与
沿着特定弧连通和
所做的特殊连通和。
即
重复以上操作最终有
再对
进行计算

①当
时如上图。
从
最右端的交叉点开始打开可得
其中
如下图
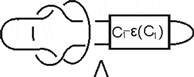
可看成如下两部分的连通和
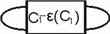
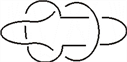
即

由于
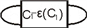
所以
(1)
同理
由于
所以上式可写成
将上式带入到(1)中得
重复以上操作,直到将
的全部交叉点都打开,可得
因此有:
②当
时如图
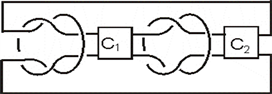
从
右端的交叉点打开可得:
其中L如图所示。
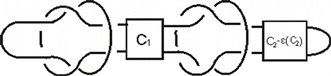
L可以看成如下四部分的连通和
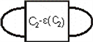



由引理3.1.1可知:

所以
同理,经逐步递推可得:
此时,
的排叉部分只剩下
个交叉点如图所示:

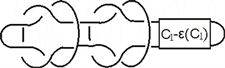
从
最右面的交叉点开始有
其中H如图3.19所示,经RII变换后可得右图
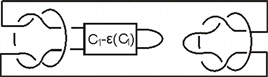
可以看成如下两部分的连通和,其中左图相当于三分支的平凡链环

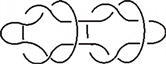
由引理3.1.1可知:
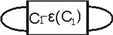
所以
综上所述,整理得
当
时,从
最右端的交叉点开始打开可得:
其中D是由k个如左图所示的链环、
个中图4和一个右图的连通和组成



由引理3.1.1和引理2.1.1可得
因此
重复以上操作,递推
次可得:
对
中的
进行一样的操作,从右面的交叉点打开得:
其中W由k个相同链环如左图所示、
个如中图所示、如右图所示的连通和
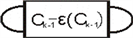


因此,
所以
递推
次可得
递推
次可得
同理,直到仅剩最后一个排叉部分
时,即对于
从
最右端的交叉点开始打开可得:
其中T由如左图所示和k个如右图所示链环的连通和
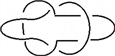
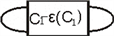
因此
所以
经以上的逐步递推全部代入到
中可得
特别的,
当
时,上式中的
仅剩下
。
当
时,上式中的
仅剩下
。
即结论成立。
拧数的计算将
分成
部分和
部分,其中
为
的部分拧数,如图所示

i) 计算
部分的拧数
若
、 为奇数、
时,如图所示,有
、、、、、、、都有
所以无论
如何定向,都有
ii) 计算所有
部分的拧数
若
且
时,如图所示,
中每一个交叉点处都是+1,所以有

同理
且
时,
且
时,
且
时,有
所以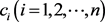 部分交叉点的拧数是由
以及
的正负决定的,且满足
部分交叉点的拧数是由
以及
的正负决定的,且满足
综合(i)、(ii)及拧数的定义可得结论,即
综上所述即由Jones多项式的定义可知
文章引用
郑 玮,庚东雨,赵璐莹. 一类链环的Jones多项式
The Jones Polynomials of Class of Knots[J]. 应用数学进展, 2019, 08(05): 1024-1035. https://doi.org/10.12677/AAM.2019.85117
参考文献
- 1. 姜伯驹. 绳圈的数学[M]. 大连: 大连理工大学出版社, 2011: 53-69.
- 2. 郑淑芳. 几何结构在Brunnian链环的琼斯多项式计算上的应用[D]: [硕士学位论文]. 长春: 东北师范大学, 2009.
- 3. Adams, C.C. (2004) The Knot Book. W.H. Freeman and Company, New York.
- 4. 戈鋆. 排叉链环的行列式[J]. 厦门大学学报, 2015, 54(6): 438-479.
- 5. Jin, X. and Zhang, F. (2004) Zeros of the Jones Polynomials for Families of Pretzel Links. Physica, 333, 183-196.
https://doi.org/10.1016/j.physa.2003.10.085
- 6. Chan, T.H. (2000) Polynomials for a Family Brunnian Links. Journal of Knot Theory and Its Ramifications, 9, 587-609.
https://doi.org/10.1142/S0218216500000335
NOTES
*通讯作者















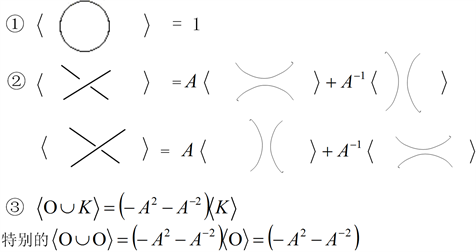



















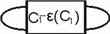


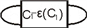


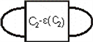








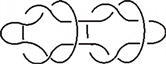
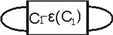



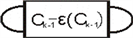



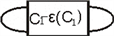



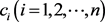 部分交叉点的拧数是由
以及
的正负决定的,且满足
部分交叉点的拧数是由
以及
的正负决定的,且满足