Advances in Applied Mathematics
Vol.
08
No.
12
(
2019
), Article ID:
33591
,
12
pages
10.12677/AAM.2019.812238
A High Resolution Upwind Scheme for Traffic Flow on Networks
Wenbin Sun, Wei Gao
School of Mathematical Sciences, Inner Mongolia University, Hohhot Inner Mongolia

Received: Nov. 28th, 2019; accepted: Dec. 17th, 2019; published: Dec. 24th, 2019

ABSTRACT
In this paper, the hyperbolic conservation law is used to describe the change law of the traffic flow density. Some typical examples of traffic flow problems are numerically simulated with a HPUS high-order bounded scheme that satisfies both CBC condition and TVD constraint. The results show that the scheme can effectively suppress non-physical oscillations near the discontinuities, and has good performance of numerical approximation.
Keywords:Finite Volume Method, Traffic Flow Model, Hyperbolic Conservation Law

网络交通流模型的高分辨率迎风格式
孙文彬,高巍
内蒙古大学数学科学学院,内蒙古 呼和浩特

收稿日期:2019年11月28日;录用日期:2019年12月17日;发布日期:2019年12月24日

摘 要
本文利用双曲守恒律方程描述车流密度的变化规律,选择一种同时满足CBC (Convection Boundedness Criterion)准则和TVD (Total Variation Diminishing)限制条件的HPUS高阶有界格式,并利用该格式对交通流问题中的一些典型算例进行数值模拟,对比结果表明该格式在间断处可有效抑制非物理振荡,并具有良好数值逼近效果。
关键词 :有限体积法,交通流模型,双曲守恒律

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
交通流问题一直是计算流体力学研究的主要方向。现代交通流理论研究始于上世纪30年代初期,1935年Greenshields提出用速度-密度线性模型描述道路车流量与车速间的关系 [1]。1936年Adams在论文中提出将道路车流量看作随机独立变量 [2],利用概率论知识来讨论车流量与车速之间的关系。1950年左右,人均汽车使用率显著提高,城市道路交通系统建设加快,James Lighthill、Gerald Whitham [3] 和Richards [4] 提出将流体力学的概念应用于交通问题中,即宏观交通流连续介质理论(经典LWR理论),该理论旨在将车流比拟为某种连续流体,利用相关双曲守恒律方程来描述车流密度的基本变化规律,此外还提出了相关的激波理论。
交通流问题的关键在于求解上述双曲守恒律方程,一般很难求得该类方程的精确解,故需要构造一些数值格式来求其数值解。但主要的求解困难在于,即使初始条件充分光滑,其数值解也会随时间的变化在某一时刻产生间断。当前求解该类方程的数值计算方法有很多,如有限差分法、有限元法、有限体积法等。有限差分法在处理简单问题时效率较高,但不适于复杂区域问题;有限元方法在处理复杂边界问题时具有较大优势,但面对大梯度问题时较为困难,有限体积法是基于无结构网格下,处理强间断问题或大梯度问题的一种高效方法。
现有的经典数值格式有一阶迎风格式FOU (First-Order Upwind)、Lax-Friedrichs格式 [5],这些格式精度较低,数值耗散较大。而中心差分格式CD (Central Difference)、二阶迎风格式SOU (Second-Order Upwind)、QUICK格式 [6] (Quadratic Upstream Interpolation for Convective Kinematic)、CUI格式 [7] (Cubic Upwind Interpolation)数值耗散较低,在光滑初值下可达到二阶及以上的精度,但在间断初值上讨论时格式不满足对流有界性,易在间断解处产生非物理振荡。为了在间断处抑制振荡,Gaskell和Lau提出CBC准则 [8] (Convection Boundedness Criterion),可以保证数值格式的对流有界性,但并不能保证数值格式的精度。1983年,Harten提出高分辨率TVD [9] (Total Variation Diminishing)全变差格式,在满足有界性的同时保证了格式的高分辨率。本文利用一种既满足TVD限制条件又满足BAIR准则的HPUS [10] (Hermite Polynomial Upwind Scheme)高阶有界格式对以下交通流密度方程进行数值模拟得到流体的运动规律,进而解决流体运动中遇到的实际问题。
本文主题内容安排如下:第二节介绍网络交通流模型的相关背景,并简要分析两种情况下交叉点处流通量的判别情况;第三节简要分析HPUS格式的构造过程;第四节利用HPUS格式对网络交通流模型中的两种情况进行数值模拟,并对结果进行分析;第五节对上述工作进行简要总结。
2. 网络交通流模型
2.1. LWR模型
在单一路径中,非线性交通流问题可转化为如下双曲守恒律方程,并利用此方程来描述车流密度的变化规律 [3] [4]
其中 表示t时刻时不同位置的车流密度, 表示该路段可达到的最大车流密度。 表示流通量,指单位时间单位面积内的车流通量,该函数为严格凹函数,v是给定的只与密度有关的光滑单调递减函数,通常我们假设 。由于函数 为严格凹函数故必存在唯一的极大值点 ,称其为临界密度,且满足 。当 时,上述流量被认为是自由流动的,函数 为密度的增加函数;而当 时,函数 为密度的递减函数,表明此时路上出现堵塞情况。
本文所研究的路网模型包含有限条路 [11],这些路交汇于某些交叉点处。例如在交叉路口J处,包含n条入路记作 ,m条出路记作 ,记入路车流密度为 ,出路车流密度为 ,交叉口J处满足入路车流总流量等于出路车流总流量:
每条出路的车流量分布可由如下交通流分布矩阵A表示 [12] :
其中 为流量分配系数,表示车量从入路i驶入并从出路j驶出的百分比。
网络交通流模型中道路交叉点的处理起到至关重要的作用,一个固定交叉点J处的Riemann问题即可表示为一个带初值的Cauchy问题,且其初值在交叉点处的每条道路上都是常数。上述双曲守恒方程在整个路网结构下的Riemann解是由每一交叉点处的Riemann解演化而来,为了在交叉点处取到Riemann问题的唯一解,需满足以下条件 [13] [14] :
1) 矩阵A每一列的百分比相加和为1,即:
2) 当满足条件1时,流通量函数 的最大值在交叉点处取到。若入路数比出路数多时,即当 时,此结论不成立;
3) 当入路数比出路数多时,即当 时。现假设交叉点入口处有a,b两条路,出口处只有c一条路,从a,b两条路驶入的车不一定都能从c驶出,可能有一部分会滞留在交叉口J处,故在出路c上要设定一个最大输出量Q,设 为路径参数,记从入路a进来的车流量为 ,从入路b进来的车流量为 。
可以发现在交叉口处求解Riemann问题相等于在每条路上求解方程的初边值问题,由于方程的非线性性,初边值问题的解可能达不到边界值,所以必须对每条道路的最大流量进行限制 [15]。
现假设每条路的初始车流密度为: ,密度严格最大值即临界密度为 ,此时入路的最大流通量 满足:
出路的最大流通量 满足:
其中 为密度最大值点,有 成立,由上式可知在交叉口处入路流通量小于等于需求流通量,即 ,且交叉点处的出路流通量小于等于供应流通量,即 ,一些车流密度会在交叉点处根据上述式子重新确定。
2.2. 交叉点处流通量
交通流的问题关键在于如何确定交叉点J的流通量,本文主要讨论以下两种路网结构的黎曼问题:(A)一条入路和一条出路(Bottelneck问题);(B)两条入路和一条出路。
2.2.1. 一条入路a和一条出路b
考虑最简单的由一条入路a和一条出路b构成的交通路网问题。首先根据入路、出路最大流通量的定义式分别确定入路a和出入b在交叉点J处最大流通量 、 ,之后取二者的最小值记为交叉点J处的流通量,记作:
则J处入流道和出流道的车流量取为:
2.2.2. 两条入路a、b和一条出路c
考虑由两条入路a、b和一条出路c构成的交通路网模型,首先同样根据入路、出路最大流通量的定义分别确定入路a、入路b和出路c在交叉点J处的最大流通量 、 、 ,此时交叉点处的流通量需分两种情况:
Case1:两条入路在J处的最大流通量之和小于出入在J处的最大流通量,即当 时,两条入路的车流均可顺利通过交叉点到达出路c,则记
Case2:两条入路在J处的最大流通量之和大于出入在J处的最大流通量,即当 时,两条入路的车流量之和超出出路c可承受车流量,故两条入路的车流需按2.1中条件3中所给出的比例进入c车道。现取路径参数为
,此时c车道上的最大流通量为
,则由路a驶入路c的车流量为
,由路b驶入路c的车流量为
,则交叉点J处三条路的实际流通量应满足以下三种情况:
时,两条入路的车流量之和超出出路c可承受车流量,故两条入路的车流需按2.1中条件3中所给出的比例进入c车道。现取路径参数为
,此时c车道上的最大流通量为
,则由路a驶入路c的车流量为
,由路b驶入路c的车流量为
,则交叉点J处三条路的实际流通量应满足以下三种情况:
1) 当 时,则有
2) 当 时,则有
3) 当 时,则有
则交叉点J处入路a、b和出路c的车流量分别取为:
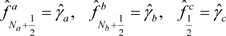
3. HPUS格式
由前文可知一维非线性交通流双曲守恒方程为
(1)
其中 表示t时刻时不同位置的车流密度, 表示流通量,指单位时间单位面积的车流通量,现利用有限体积法对上述方程进行空间离散。
3.1. 空间离散
首先将区间 平均剖分成N个控制单元,记: ,每个控制单元记为 ,现定义控制单元的积分平均值为: 。
在区间 上对方程(1)进行积分化简得:
上对方程(1)进行积分化简得:
其中 、 分别为 、 的近似值。
之后引入全局Lax-Friedrichs数值流通量来确定 的值 [16]
其中 ,之后利用HPUS格式重构 。
3.2. 对流有界性
现取三个相邻的网格节点U、C、D分别表示上游、中心、下游网格节点如图1所示,这三个节点所

Figure 1. Three neighboring mesh points and the mesh face
图1. 三个相邻节点与单元边界
对应的函数值分别为 ,取f表示均匀网格上的界面,则 表示均匀网格的界面值,通过相邻的三个节点对其进行重构,可将一些常见的线性格式统一为如下表达式:
其中 ,此时 的取值与 有关,由如下Leonard正则化思想 [17]
将上述格式转化为如下正则化形式(Normalized Variable Formulation, NVF)为
发现正则化后 的值只与 和参数k有关,表1给出几种常见线性对流格式正则化前后的形式:
Table 1. System resulting data of standard experiment
表1. 几种常见线性对流格式及其正则化格式
这些格式在光滑初值下都可达到二阶及以上的精度,但对于间断初值不满足对流有界性,在间断解处产生非物理振荡。为了在间断处有效抑制振荡,Gaskell和Lau提出了CBC准则 [8],但CBC准则只能保证数值格式的有界性,并不能保证数值格式的精度,为了提高数值格式的精度,Wei和Hou提出BAIR准则,即改进的CBC准则 [18] [19] :
此外,TVD约束条件在归一化变量公式可定义为
现以 图为横坐标, 为纵坐标将BAIR准则和TVD约束条件表示在图2中,当格式的NV线落在图中阴影部分时表示该格式既满足BAIR准则又满足TVD约束条件。

Figure 2. The regions of the TVD (shaded) and BAIR (hatched)
图2. BAIR区域(虚线部分)和TVD区域(阴影部分)
3.3. 对流项离散
现已知高分辨率格式在归一化变量公式下可统一表示为: ,由Zijlema和Wesseling所提出的结论可知 [20],下列性质适用于这类格式:
1) 若对流格式的NV线过点 ,则该式具有二阶局部截断误差。
2) 对流格式的NV线需满足 。
3) 为使对流格式同时满足BAIR准则和TVD约束条件,格式的图像应落在图中阴影部分且 。
故所取对流格式需满足:当 时,方程需过点 ,点 与点 ,且满足 ,,,由图可知当 , 时,格式的图像落在阴影部分。
现取 , 得满足上述条件的HPUS格式为:
3.4. 时间离散
空间离散之后方程变为只与时间有关的常微分方程,为了有效的抑制振荡,利用三阶Runge-Kutta方法对时间进行离散,三阶R-K格式如下:
4. 数值算例
本节我们将运用上述HPUS格式对文献 [13] [14] [16] 中两个较为复杂的路网模型进行数值模拟,并将Jiang、Shu所提出的五阶WENO格式 [21] 在4000个网格点上对方程进行数值模拟的结果记为参考解,图像上表示为“Reference”。以下数值算例中,三阶(SSP)-RK方法均在CFL条件下使用。
4.1. Bottleneck问题
Bottleneck问题为交通流的不同宽度的单一路径模型,由一条较宽的入路Road a和一条较窄的出路Road b构成,J表示两条道路的相交点即节点。由于两条路具有不同的宽度,从而两条道路具有不同的流通量函数。Bottleneck问题的实质即讨论不同宽度单一路径模型中从宽的入路a到窄的出路b的车流密度变化规律。
首先在计算区间[0,2]上考虑交通流双曲守恒方程 ,取 ,[0,1]区间表示较宽的入路车道a,所对应的流通量函数为
当 时,可取到入路a上的最大流通量: ,
则[1,2]区间表示较窄的出路车道b,所对应的流通量函数为
当 时,可取到出路b上的最大流通量: 。
现假设 分别表示入路a和出路b的t时刻不同位置的车流密度,取N = 200,CFL = 0.05,下面讨论不同初值条件及边界条件下的瓶颈问题。
情形1:初值条件及边界条件为:
其中初始条件所给车流密度趋于出路b的最大车流密度,随着时间推移我们可以观察到交通堵塞的形成,详见 [13]。现利用HPUS格式求解时间T分别为0.5,1.0,4.0时的数值解,并在图3中与五阶WENO格式所给出的参考解进行对比分析。
情形2:初值条件及边界条件为:
利用HPUS格式计算时间T为2.0,4.0,10.0时的数值解,并在图4中与五阶WENO格式所给出的参考解进行对比分析。
情形3:初值条件及边界条件为:
利用HPUS格式计算时间时间T为0.2,0.5,0.7时的数值解,并在图5中与五阶WENO格式所给出的参考解进行对比分析。
由图3~5可知HPUS格式可以很好的近似参考解,在间断处及大梯度处都可以有效地抑制非物理震荡。

Figure 3. Bottleneck problem with initial and boundary data—Case 1
图3. 情形1初边值条件下Bottleneck问题的数值解

Figure 4. Bottleneck problem with initial and boundary data—Case 2
图4. 情形2初边值条件下Bottleneck问题的数值解

Figure 5. Bottleneck problem with initial and boundary data—Case 3
图5. 情形3初边值条件下Bottleneck问题的数值解
4.2. 两条入路一条出路模型
现考虑图6所示的包含两条入路车道a,b及一条出路车道c的交叉口情况,每一条路的计算区间均取[0,1],每条路的流通量函数皆满足 。

Figure 6. A junction with two incoming and one outgoing roads
图6. 两条入路一条出路的交叉口示意图
现给出如下初值条件:
及边界条件:
图7~9分别表示入路a,入路b,出路c在N = 500,CFL = 0.01,时间T分别取0.5,1.0时的HPUS格式数值解及五阶WENO格式参考解。由所给数值结果可知,HPUS格式数值解可以很好的近似五阶WENO格式参考解,且相较于参考解HPUS格式可以在较粗网格下达到良好的逼近效果,从而有效的提高了计算速度。
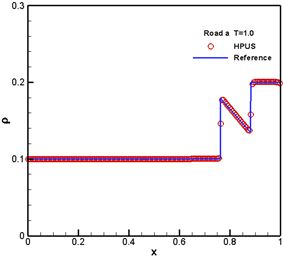
Figure 7. Numerical results for Road a at T = 0.5, 1.0.
图7. T = 0.5,1.0时Road a的数值解

Figure 8. Numerical results for Road b at T = 0.5, 1.0.
图8. T = 0.5,1.0时Road b的数值解

Figure 9. Numerical results for Road c at T = 0.5, 1.0.
图9. T = 0.5,1.0时Road c的数值解
5. 结论
本文基于交通流理论,将交通流基本规律转化为相关的非线性双曲守恒律方程,分析讨论两种简单路网模型交叉点处的流通量,在有限体积法下对上述双曲守恒方程进行数值离散,利用高分辨率Hermite多项式迎风格式逼近对流项,通过相关交通流算例分析,HPUS格式在间断处及大梯度处可以有效的抑制非物理振荡,且其数值解可在较粗尺寸的网格下达到良好的逼近效果,从而可以正确描述交通流特性,准确实时的模拟交通过程,以便于对交通堵塞等问题提前做出预判。
致谢
作者感谢审稿专家给予本文宝贵的修改意见和建议,感谢期刊编辑对于本文的付出。
基金项目
本文由内蒙古大学科研发展基金项目(21100-5187133)支持。
文章引用
孙文彬,高 巍. 网络交通流模型的高分辨率迎风格式
A High Resolution Upwind Scheme for Traffic Flow on Networks[J]. 应用数学进展, 2019, 08(12): 2072-2083. https://doi.org/10.12677/AAM.2019.812238
参考文献
- 1. Richards, P.I. (1956) Shock Waves on the Highway. Operations Research, 4, 42-51.
https://doi.org/10.1287/opre.4.1.42 - 2. Pipes, L.A. (1953) An Operational Analysis of Traffic Dynamics. Journal of Applied Physics, 24, 274-281.
https://doi.org/10.1063/1.1721265 - 3. Lighthill, M.J. and Whitham, G.B. (1955) On Kinematic Waves. II. A Theory of Traffic Flow on Long Crowded Roads, Proceedings of the Royal Society of London. Series A, 229, 317-345.
https://doi.org/10.1098/rspa.1955.0089 - 4. Payne, H.J. (1973) Freeway Traffic Control and Surveillance Model. Journal of Transportation Engineering, 99, 767-783.
- 5. Spalding, D.B. (1972) A Novel Finite Difference Formulation for Differential Expressions Involving Both First and Second Derivatives. International Journal for Numerical Methods in Engineering, 4, 551-559.
https://doi.org/10.1002/nme.1620040409 - 6. Leonard, B.P. (1979) A Stable and Accurate Modeling Procedure Based on Quadratic Interpolation. Computer Methods in Applied Mechanics and Engineering, 19, 59-98.
https://doi.org/10.1016/0045-7825(79)90034-3 - 7. Agarwal, R.K. (1981) A Third-Order-Accurate Upwind Scheme for Navier-Stokes Solutions at high Reynolds Num bers. 19th AIAA Aerospace Sciences Meeting, St. Louis, MO, 12-15 January 1981.
https://doi.org/10.2514/6.1981-112 - 8. Leonard, B.P. (1988) Simple High-Accuracy Resolution Program for Convective Modeling of Discontinuities. International Journal for Numerical Methods in Fluids, 8, 1291-1318.
https://doi.org/10.1002/fld.1650081013 - 9. Harten, A. (1983) High Resolution Schemes for Hyperbolic Conservation Law. Journal of Computational Physics, 49, 4357-4393.
https://doi.org/10.1016/0021-9991(83)90136-5 - 10. Gao, W., Li, H. and Liu, Y. (2013) A High Resolution NV/TVD Hermite Polynomial Upwind Scheme for Convection- dominated Problems. Mathematical Methods in the Applied Sciences, 36, 1107-1122.
https://doi.org/10.1002/mma.2667 - 11. Bretti, G., Natalini, R. and Piccoli, B. (2007) A Fluid-Dynamic Traffic Model on Road Networks. Archives of Computational Methods in Engineering, 14, 139-172.
https://doi.org/10.1007/s11831-007-9004-8 - 12. Coclite, G.M., Garavello, M. and Piccoli, B. (2005) Traffic Flow on a Road Network. SIAM Journal on Mathematical Analysis, 36, 1862-1886.
https://doi.org/10.1137/S0036141004402683 - 13. Bretti, G., Natalini, R. and Piccoli, B. (2006) Numerical Approximations of a Traffic Flow Model on Networks. Networks & Heterogeneous Media, 1, 57-84.
https://doi.org/10.3934/nhm.2006.1.57 - 14. Canic, S., Piccoli, B., Qiu, J.-M. and Ren, T. (2015) Runge-Kutta Discontinuous Galerkin Method for Traffic Flow Model on Networks. Journal of Scientific Computing, 63, 233-255.
https://doi.org/10.1007/s10915-014-9896-z - 15. Garavello, M. and Piccoli, B. (2006) Traffic Flow on Networks, Volume 1. American Institute of Mathematical Sciences, Springfield, MO.
- 16. Shi, Y.F. and Guo, Y. (2016) A Maximum-Principle-Satisfying Finite Volume Compact-WENO Scheme for Traffic Flow Model on Networks. Applied Numerical Mathematics, 108, 21-36.
https://doi.org/10.1016/j.apnum.2016.05.001 - 17. Lax, P.D. and Wendroff, B. (1960) Systems of Conservations Laws. Communications on Pure and Applied Mathematics, 13, 217-237.
https://doi.org/10.1002/cpa.3160130205 - 18. Wei, J.J., Yu, B., Tao, W.Q., Kawaguchi, Y. and Wang, H.S. (2003) A New High-Order-Accurate and Bounded Sche- me for Incompressible Flow. Numerical Heat Transfer, Part B: Fundamentals, 43, 19-41.
https://doi.org/10.1080/713836153 - 19. Hou, P.L., Tao, W.Q. and Yu, M.Z. (2003) Refinement of the Convective Boundedness Criterion of Gaskell and Lau. Engineering Computations, 20, 1023-1043.
https://doi.org/10.1108/02644400310503008 - 20. Zijlema, M. and Wesseling, P. (1995) Higher Order Flux-Limiting Methods for Steady-State, Multidimensional, Convection-Dominated Flow. Report 1995-131, TU Delft.
- 21. Jiang, G.-S. and Shu, C.-W. (1996) Efficient Implementation of Weighted ENO Schemes. Journal of Computational Physics, 126, 202-228.
https://doi.org/10.1006/jcph.1996.0130
