Advances in Applied Mathematics
Vol.
10
No.
05
(
2021
), Article ID:
42596
,
9
pages
10.12677/AAM.2021.105170
基于量子粒子群算法的CT系统参数标定
武良隆,刘晓东,王彦超,刘鑫磊,陈倩华*
青岛理工大学理学院,山东 青岛

收稿日期:2021年4月21日;录用日期:2021年5月7日;发布日期:2021年5月26日

摘要
量子计算是一种遵循量子力学规律调控量子信息单元进行计算的新型计算模式,在计算效率上,量子算法在处理问题时速度要快于传统的通用计算机。提出了一种基于量子粒子群算法的CT系统参数标定。该方法首先根据螺旋CT原理和几何关系,对参数进行大致的求解,随后利用量子粒子群算法对参数进行优化,利用高斯滤波对图像进行优化,以此实现较高精度的CT系统参数标定,实验结果表明该方法不仅可以实现高效率的CT成像,而且对量子计算理论的实际应用的推广有重大意义。
关键词
CT系统,量子粒子群算法,Radon变换,高斯滤波
Parameter Calibration of CT System Based on Quantum Particle Swarm Optimization
Lianglong Wu, Xiaodong Liu, Yanchao Wang, Xinlei Liu, Qianhua Chen*
School of Science, Qingdao University of Technology, Qingdao Shandong

Received: Apr. 21st, 2021; accepted: May 7th, 2021; published: May 26th, 2021

ABSTRACT
Quantum computing is a new computing mode that follows the laws of quantum mechanics to regulate the quantum information unit for calculation. In terms of computational efficiency, the quantum algorithm is faster in reprocessing problems than the traditional general purpose computer. A calibration method of CT system parameters based on quantum particle swarm optimization (QPSO) is proposed. In this algorithm, firstly according to the principle of spiral CT and geometric relations, approximate solving the parameters, and then use a quantum particle swarm optimization (QPSO) algorithm to optimize the parameters, and optimize the image, using Gaussian filter to realize high accuracy of CT system parameter calibration, the experimental results show that this method not only can realize high efficiency of CT imaging, but also for the promotion of practical application of quantum computation theory has great significance.
Keywords:CT System, Quantum Particle Swarm Optimization, Radon Transform, Gaussian Filtering

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
以量子算法为代表的量子计算由于具有高度并行性、指数级存储容量和对经典启发式算法的指数加速作用,它们在计算复杂度、加速收敛等方面明显超过了常规算法。量子粒子群算法采用量子位对粒子的当前位置进行编码,用量子旋转门实现对粒子最优位置的搜索,用量子非门实现粒子位置的变异以避免早熟收敛。
CT (Computed Tomography)可以在不破坏样品的情况下,利用物质对射线的吸收特性对样品进行断层成像。CT成像系统在心血管系统,神经系统,肿瘤定位诊断,靶向治疗,物质分离与鉴别等方面具有广阔的发展空间 [1]。CT成像系统在安装时往往存在误差,所以需要对其进行参数的标定以减小误差,提高后续的成像质量。将量子粒子群算法应用到CT系统参数标定,仿真结果表明,该算法的寻优能力以及优化效率优于几何模型算法。本文采用2017年全国大学生数学建模赛题A数据进行分析。
2. 几何法模型的建立与求解
首先CT系统的接受信息是由射线能量经过介质吸收,然后增益后得到的数据。根据朗伯贝尔吸收
定律 [2] , 为介质长度, 为介质吸收率,上式可变换为 ,经过增益(增益为 )后, 。由于附件1中的模板吸收率均为1,所以可以简
化为 ,即与射线穿过介质的长度成正比,这也说明了附件2中的数据大小与射线穿过介质的长度成正比。在附件2中可以观察到有512 × 180个数据,即有180列数据,180个方向数据,那么这其中,必然有一个方向(与椭圆长轴平行的方向)的数据存在最大值,有另一个方向(与椭圆短轴平行的方向)含零的数据最少。经过MATLAB数据处理,可以得到射线与椭圆长轴平行的方向为第151列,在第151列数据中,可以明显看出穿过椭圆的数量为 条。射线与椭圆短轴平行的方向可能为第58,59,60,61,62,63,64,65列。假设认为射线在平行椭圆短轴方向,首末位置的数据最小。对上述短轴方向列首末位置进行相加,发现数据呈现先升高后下降、再升高再下降的形式,认为第一个极小值点对应的列为射线平行椭圆短轴方向列,即第62列,穿过椭圆的射线条数为 条。
椭圆长轴长为 ,短轴长为 。由于圆形模板尺寸较小,贡献不大,将其忽略。根据上述
条件可以求得探测器单元之间的距离: 。模板信息如图1所示:
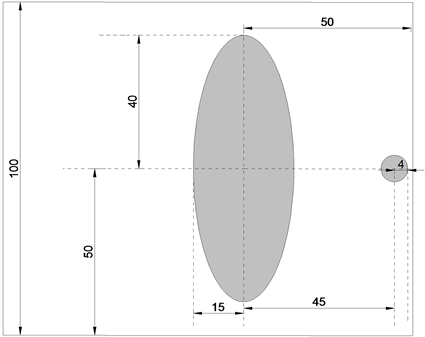
Figure 1. Template dimension drawing
图1. 模板尺寸图
以椭圆中心为原点,椭圆短轴为x轴,椭圆长轴为y轴,建立直角坐标系。大多数CT系统旋转中心位于CT系统几何中心 [3],只要知道任意两条方向下射线中线方程,两者的交点即为旋转中心位置。射线平行于椭圆长轴时,长轴位于第223行,射线平行于椭圆短轴时,短轴位于第232行。平行于长轴时,中线方程为
平行于短轴时,
因此旋转中心的位置为 。
因为CT系统均匀旋转(意味着每次旋转转过的角度相同),并且射线与椭圆长轴平行时,夹角为90˚,射线与椭圆短轴平行时,夹角为0˚。并且根据附件2可知,从0˚到90˚共旋转151 – 62 = 89次,所以每次旋转转过的角度为 ,初始位置与水平线的夹角为 ,因此旋转次数与夹角的关系为 。
3. 根据几何模型标定参数进行Radon逆变换
根据附件2中的数据和几何模型标定参数进行Radon逆变换,即可得到每一点的密度函数值,对其进行裁剪然后利用最近邻插值算法对变换后的矩阵进行缩小,得到256 × 256个数据,这与附件1数据相同。由各点密度函数值进行图像重建后,可以得到模板的位置和几何形状,其吸收率不确定,但是可以知道吸收率与密度函数之间是成正比关系的。根据附件1中的数据 和经过变换得到的数据 ,就可以求得比例系数。对 可以得到每一点的比例系数,但是由于每一点并不是一一对应的。观察数据可以看出,大部分点的比例系数在0到3之间,那么对这些比例系数加和取平均,可以求得比例系数为 。根据附件1数据和经过变换得到的数据进行二维像素图比较,再加入比例系数对图像进行三维建模比较,如图2、图3所示。

Figure 2. Two-dimensional pixel map
图2. 二维像素图

Figure 3. Three-dimensional model
图3. 三维模型图
从图中可以看出,经过Radon变换三维建模后的图像与实际图像相比,在顶面较水平,但从完整性来看,两者差别较大。
4. 基于量子粒子群算法的模型优化
运用几何模型标定的参数进行Radon逆变换,可以发现进行复原的图像与实际图像出现了位置的偏移,主要原因是运用几何模型标定的角度参数精度不够,因此对系统参数的标定是尤为重要的。接下来用量子粒子群算法对该系统重新进行参数的标定,量子粒子群算法具有搜索能力和优化效率高于普通粒子群算法的优点。
4.1. QPSO算法
粒子群优化算法(Particle Swarm Optimization, PSO)是美国心理学家Kennedy和电气工程师Eberhart受鸟类捕食行为的启发,于1995年提出的一种群智能优化算法 [4]。将改进后的量子进化算法(QEA)融合到PSO中,李士勇和李盼池提出一种新颖的量子粒子群优化算法(Quantum Particle Swarms Optimization, QPSO) [5]。该算法采用量子位的概率幅来对粒子的位置进行编码,用量子旋转门实现对粒子位置的移动,用量子非门实现对粒子位置的变异以避免提前收敛。首先应该建立一个目标函数,由前面Radon变换分析可知附件1的数据 与附件2经过逆变换后的数据 的差异越小,则说明建模后的图像与实际图像越接近,因此建立这样一个目标函数 [6] [7]:
其值可以作为粒子的适应度。
以射线初始角度和每次旋转的角度为优化变量 ,建立二维空间,其中 , 为自变量的定义域。
下面给出具体的实现步骤:
(1) 产生初始种群
在QPSO中,直接采用量子位的概率幅作为粒子位置进行编码,并且考虑到初始位置的随机性,采用如下所示编码方式:
,
其中 , 为 之间的随机数; , 为种群规模,这里取50;其中这些粒子占据量子态 和 两个位置(余弦位置和正弦位置),对应的概率幅为:
(2) 解空间变换
在QPSO中,由于每个粒子在原空间每个维度可遍历的范围为 ,为了计算每个粒子在当前位置的优劣性,需要对原空间进行映射,将其映射到对应的解空间。设粒子 上第 个量子位为 ,那么对应的解空间变量为:
由此可见,每个粒子对应两个解: 的概率幅 对应 , 的概率幅 对应 ,其中 ,。
(3) 粒子状态更新
在传统PSO中,需对粒子进行速度和位置的更新,而在QPSO中,将速度的更新变为量子位幅角增量的更新:
其中 是惯性因子; 是常数,它们分别称为自身因子和全局因子; 是 之间的随机数;
将位置的更新变为量子位概率幅的更新(基于量子旋转门):
其中 ,。
(4) 变异处理
在QPSO中,引入量子非门作为变异算符,来避免算法的提前收敛:
其中 ,。
(5) QPSO算法步骤:
Step 1 粒子群初始化。
Step 2 进行解空间变换,代入目标函数。如果粒子在当前的位置比自身记忆的最优位置还要优秀,就用当前位置替换最优位置,全局最优位置也是如此操作。
Step 3 对粒子进行量子幅角度和量子概率幅的更新。
Step 4 依照变异概率,对每个粒子进行变异操作。
Step 5 回到Step 2继续循环执行程序,直到满足收敛条件或者到达迭代次数。
其中QPSO参数设置:限定迭代次数200,惯性因子为0.5,自身因子为2,全局因子为2,变异概率为0.05。
4.2. 模型的求解
对于该算法,虽然没有量子计算机,但是可以利用MATLAB和QPSO算法的逻辑进行编程求解(这也进一步说明了该量子算法的逻辑可行性),在第200代得到每次旋转转过的角度为1.002204671366208,初始时刻射线与水平线的夹角为−60.000000018920070,利用优化后的参数和附件2,对模板重新进行建模处理,求得结果如图4、图5所示:

Figure 4. Two-dimensional pixel image based on QPSO
图4. 基于QPSO的二维像素图

Figure 5. Three-dimensional model graph based on QPSO
图5. 基于QPSO的三维模型图
将图3与图5进行对比,可以很明显的看出基于QPSO算法模拟重建的二维像素图与实际图更加接近,只有在下方有些许瑕疵,三维模型图的平面也更加的完整,整齐。下面将结果代入目标函数f,由目标函数的定义可以知道,它代表着模拟图与实际图之间的差异,因此目标函数越小说明模型效果越好,结果如表1所示,从表中可以明显看出QPSO算法更加的高效,准确。
在上述目标函数中,为了提高计算速度,没有将 乘以比例系数,现在将其乘入,并对图像进行高斯滤波,再将其代入目标函数(记为 ),此时结果如表1所示:
从表中可以看出,基于QPSO算法与高斯滤波的图像更加准确,差异最小。经过滤波后的三维重建图如图6所示:
Table 1. The comparison of objective function of each algorithm and the comparison of the optimized objective function
表1. 各算法目标函数对比以及优化后目标函数对比
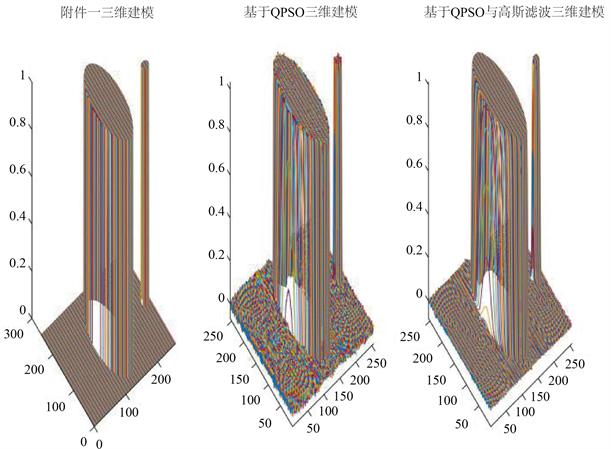
Figure 6. 3D reconstruction based on QPSO and Gaussian filter
图6. 基于QPSO与高斯滤波的三维重建图
从图中可以看出,基于QPSO与高斯滤波的三维重建图在上表面基本与原图一致,并且更加的光滑完整。此时,精度为1减去差异项的最小值,即1 − 0.0160 = 98.4%,这也进一步说明了QPSO算法的重要性。
5. 结论
本文首先利用几何分析求得CT系统各参数,基于Radon变换对模板进行重建,但精度不够,又基于量子粒子群算法这一高效智能优化算法对参数进行了改进,并在最后利用高斯滤波器对图像进行了进一步的处理,结果几乎与原图一致,这为接下来的处理其他物体的图像复原奠定了基础。并且基于量子位概率幅编码机制使QPSO不仅扩展了对空间的遍历能力,而且基于量子旋转门的粒子移动方式也使搜索变得更为精细。同时,该量子算法的应用也可以对处理其他问题提供思路。
基金项目
2020年山东省大学生创新训练项目(项目编号S202010429197)和2019年青岛理工大学教学改革项目(项目编号F2019-041)资助。
文章引用
武良隆,刘晓东,王彦超,刘鑫磊,陈倩华. 基于量子粒子群算法的CT系统参数标定
Parameter Calibration of CT System Based on Quantum Particle Swarm Optimization[J]. 应用数学进展, 2021, 10(05): 1607-1615. https://doi.org/10.12677/AAM.2021.105170
参考文献
- 1. 张磊. 能谱CT成像原理及临床应用价值研究[J]. 中国卫生产业, 2016, 13(29): 33-35.
- 2. 郭立倩. CT系统标定与有限角度CT重建方法的研究[D]: [硕士学位论文]. 大连: 大连理工大学, 2016.
- 3. 孟凡勇, 李忠传, 杨民, 李静海. 基于投影原始数据的CT旋转中心的精确确定方法[C]//第十三届中国体视学与图像分析学术会议, 2013, 18(4): 336-341.
- 4. Kennedy, J. and Eberhart, R.C. (1995) Particle Swarms Optimization. Proceedings of the IEEE International Conference on Neural Networks, 4, 1942-1948. https://doi.org/10.1109/ICNN.1995.488968
- 5. 李士勇, 李盼池. 求解连续空间优化问题的量子粒子群算法[J]. 量子电子学报, 2007, 24(5): 569-574.
- 6. 宫珊珊, 梅立峰, 廖志良, 黄旭辉. 基于粒子群算法的CT系统参数标定及优化[J]. 安徽建筑大学学报, 2018, 26(6): 87-91.
- 7. 云浩, 赵碧华, 孙文才. 螺旋CT原理、技术特点及临床应用[J]. 医疗装备, 2003(9): 4-6.
NOTES
*通讯作者。
