Advances in Applied Mathematics
Vol.
10
No.
06
(
2021
), Article ID:
43218
,
13
pages
10.12677/AAM.2021.106216
均值方差准则下的投资与再保险 对比研究
蔡 畅,刘方盈*
武汉理工大学统计学系,湖北 武汉
收稿日期:2021年5月17日;录用日期:2021年6月3日;发布日期:2021年6月18日

摘要
本文旨在研究保险公司在终端时间确定情形下的最优适应性和确定性投资与再保险问题,首先假定保险公司的盈余可以投资于一个无风险资产和一个风险资产,再保险的形式为比例再保险,然后分析风险资产投资与再保险的综合财富过程,通过建立适当的均值–方差模型,运用如HJB方程等方法,求解对应问题中的最优投资和再保险策略的解析表达式,对比分析该情形下发现确定性策略结果皆优于适应性策略。最后分析获得的最优策略与经济参数的关系,得出一般结论:当风险资产的预期回报率或其波动率减小时,最优投资比例增大;当保险盈余的收益率或其波动率减小时,最优再保险比例增大;当再保费率相对保费的安全负载增大或再保费安全负载增大时,最优再保险比例也会增大。
关键词
比例再保险,均值–方差准则,HJB方程,最优确定投资策略

Comparative Study of Investment and Reinsurance under the Mean-Variance Criterion
Chang Cai, Fangying Liu*
Statistic Department, Wuhan University of Technology (WHUT), Wuhan Hubei
Received: May 17th, 2021; accepted: Jun. 3rd, 2021; published: Jun. 18th, 2021

ABSTRACT
The aim of this paper is to study the optimal deterministic and adaptive investment and reinsurance of insurance companies in the case of deterministic terminal time. First, we assume that insurance company can invest in a risk-free asset and a risky asset, re the form of a proportional reinsurance, then analyze process of comprehensive wealth with risk assets investment and reinsurance, through the establishment of appropriate mean-variance model, and use methods such as HJB equation, the analytical expressions of the optimal investment and reinsurance strategies in the corresponding problems are solved, and the results of the deterministic strategies are found to be superior to the adaptive strategies under the comparative analysis of this situation. The uncertainty of investment termination time is further discussed. The general conclusion is drawn: the expected rate of return of a risky asset increases or its volatility decreases, the optimal investment proportion increases; the yield of insurance surplus increases or its volatility decreases, the optimal reinsurance ratio increases; the reinsurance rate relative to the safe load of the premium or the safe load of the premium increases, the optimal reinsurance ratio will also increase.
Keywords:Proportional Reinsurance, Mean-Variance Criterion, HJB Equation, Optimal Deterministic Investment Strategy

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1.1. 研究背景
目前,关于最优再保险和最优投资方面的研究逐渐成为随机控制及保险精算领域中的热点问题,而如何找到最优的投资策略、再保险策略以达到保险公司的经营目的,对保险公司的发展来说是一个更具有现实意义的问题。现如今,保险资金的投资作为保险公司重要的收入来源之一,投资策略的选择很大程度上影响者保险公司的收益。针对投资策略的研究通常与金融数学中的投资组合理论紧密相关,本文考虑保险公司将其盈余资金投入到包含一个风险资产和一个无风险资产的金融市场,选择一个最优投资策略即是选择一个最优投资组合。作为分散风险的手段,再保险可使保险人避免索赔风险过于集中的问题,对保险公司的经营能起到一定的稳定作用。
1.2. 研究现状
面对着激烈的行业斗争,保险公司从降低保险销售成本和提高投资收益两个方向积极努力,进行正确的投资是提高投资收益、风险管理评估的关键。投资策略提供更高的收益水平,也可以降低保险费中的资金成本,达到降低险种保费的作用。现在,很多学者对保险精算中的投资与再保险问题进行了较为深入的研究。
索赔过程是再保险问题中需要着重刻画的问题,其中,Y. Cao, N. Wan (2009) [1] 在比例再保险下讨论了以最大化终点财富效用函数为目标的最优投资策略问题,假设所考虑的理赔过程遵循一个带有漂移项的BM过程,且允许保险人投资于无风险资产和风险资产,并求解相应的HJB方程,导出了比例再保险以及投资于风险资产的最优策略的表达式。风险模型的适用性会随着市场的不确定性而发生着改变,林祥,李娜(2011) [2] 对索赔次数满足复合Poisson——Geometric过程的风险模型进行分析求解,假设保险公司的盈余可以投资于风险资产,研究以破产概率最小为目标,在配置比例再保险的策略下以及在保险公司的盈余和投资具有不确定性的条件下,得到了最优策略的表达式;桂有利(2009)等人 [3] 也对不确定情况下的跳-扩散风险的最优投资和再保险进行了研究。在投资者对风险的态度问题上,王宁(2020) [4] 主要从以下两个方面讨论了连续时间模型下的投资与再保险优化问题:1) 阐释保险公司的决策过程是如何受到决策者的模糊厌恶态度影响的;2) 研究两个不同保险公司决策者之间的交互作用影响。很少有学者研究策略中索赔的相关性,而Chen, Z., Yang, P. (2020) [5] 考虑了具有价格跳跃和相关索赔的不确定性的保险公司的鲁棒最优再保险与投资策略选择问题,相关索赔的模糊厌恶保险人(AAI),通过外推偏差来衡量未来的索赔与历史索赔的相关性,进一步研究了在三个典型情况下的最优投资与再保险策略之间的关系。由于金融市场中会存在模式的变化,李悦(2018) [6] 就研究了具有模式转换下保险公司的最优投资和再保险策略问题,通过改进传统的模式转换模型,求解最优控制问题,得到连续的最优策略;杨鹏(2014) [7],Qiang Zhang, Ping Chen (2018) [8] 研究了基于均值–方差准则下的保险市场上的最优投资再保险问题,投资时风险资产满足CEV模型,并应用线性二次控制的理论求得最优策略和值函数的显式解。衡量终端财富产生的效果的标准不同,得到的策略也会有所差异。上文主要是通过均值–方差或指数效用最大化来解决所研究的问题,而罗琰,杨招军(2009) [9] 则研究了保险公司的比例再保险与最优投资问题,通过运用随机控制理论,分别使得退出系统时刻期望效用准则和生存概率准则最大化,得到保险公司的最优投资和再保险策略的表达式。上文大多数研究了随机投资的情形,而N. Bäuerle, Rieder U. (2013) [10] 文中对比研究了适应策略和确定性投资策略的理论,作为优化准则,该文较为全面的处理了均值–方差问题、其他风险度量问题、指数效用问题和破产概率问题,研究发现基于这些准则下的最优投资策略之间存在一些有趣的联系。
近些年来,有许多学者从其他不同的角度对保险公司的资产配置与风险管理问题进行了一定的深入研究。其中,Yao H., Li Z., Duan L. (2016) [11] 研究了一种多阶段的均值–方差投资策略选择问题,其中涉及的随机利率满足离散时间的Vasicek模型,运用动态规划方法和拉格朗日对偶理论,推导出均值–方差模型的投资策略的解析表达式和有效边界。Zeng, Li (2011) [12] 假定保险公司的盈余过程满足近似扩散过程,而保险公司投资的金融市场由以下两类资产组成:风险资产和无风险资产;在均值方差准则下运用随机动态规划理论,得到了保险公司的最优投资与再保险策略的解析形式及有效边界。Guo (2014) [13] 在满足投资人的投资心理为损失厌恶的条件下,只研究和分析了保险公司的最优资产分配问题。文中假定保险公司的投资市场由风险资产和无风险资产这两类资产构成,风险资产满足GBM模型;而保险公司的盈余过程则由经典的Cramer-Lundberg模型描述。
1.3. 研究框架
本文结构如下:下文介绍了论文工作的开展所涉及的金融模型和一些基本假设,并考虑了一般均值–方差准则下的确定性与适应性下投资与再保险的最优问题,并分析了确定性与适应性情形下最优投资与再保险策略的对比研究。通过数值模拟分析了模型中所涉及的参数对最优策略的影响,得出了一般性结论,并解释其经济学含义。
2. 正文
本章建立了研究保险投资与再保险问题所涉及的模型。首先,保险公司可以通过比例再保险方式来收取保费,假定保险公司的盈余过程满足扩散近似过程;而金融市场由无风险资产和风险资产这两个资产组成,而风险资产的价格过程服从几何布朗运动;然后分析保险公司的财富过程,研究兼顾风险和收益的最优投资与比例再保险模型;假定保险公司的投资决策在给定均值的情况下使得风险最小化,利用HJB方法,给出最优保险投资策略与最优再保险策略的解的形式。最后,分析了各个经济意义下的参数等对所求得的最优策略的影响,并给出了相应的经济学意义上的解释,为保险事业作参考价值。
2.1. 基本模型
考察完备概率测度空间 ,本文中假定所涉及到的随机过程都在概率空间 上有定义,且皆为适应过程。接下来将介绍本文开展的工作需要涉及到的模型如下。
2.1.1. 保险公司理赔过程
保险公司的财富过程可以简化为两个部分——盈余过程和投资过程。其中盈余过程又可以拆分为下面三个组成方面:保险人收取保费,并支付再保险费用和支付理赔费用;而投资过程这里先假设只考虑两种资产,简化模型方便计算 [6]。
考虑有限的连续时间 ,给定一个完备概率空间 ,在其上定义两个一维的标准布朗运动 和 ,并假设这两个布朗运动 和 之间是相互独立的,分别代表保险赔付过程的随机性和金融市场中风险资产的随机性。令 和 分别代表 和 产生的自然信息流。令
(1)
记 是概率测度P下的期望。
1) 假设本文所考虑的整个保险公司的保费收入为 ,则实务中保险费用的确定需依据复杂地计算每个保险种类的责任才可以得到。假设保险公司的保费是经验赔付金额的一定比例,则有
(2)
其中, 是理赔费用的均值,而 是一个安全负载系数,为能保证在该保险费用下,保险公司可以盈利。
2) 本文所采用再保险方式为比例再保险,假设t时刻保险公司的再保险比例水平为 ,则 称为保险公司的风险暴露水平,即保险公司的自留水平。若 已确定,则保险公司需要支付每次索赔额的 ,而剩下的由再保险公司赔付,现记 表示t时刻发生的理赔金额。保险公司需要支付给再保险公司的再保费满足:
(3)
其中, 是一个再保险费用安全负载系数, 可满足实际上保险的再次保险生效,以达到再保险公司盈利的目的。
3) 假设保险公司的理赔过程 满足如下的扩散近似模型,实际上,扩散近似模型适用于保险组合规模较大且单个索赔额较小的情形。保险公司在承担保险的过程中可能会受到外在等随机因素的影响,理赔过程 服从如下式(4)的近似扩散过程:
(4)
其中, 是一个正的漂移项, 是一个标准布朗运动。上式(4)理赔过程中波动部分的系数是负的,以上两种对比情况的分析可以知道,当赔付较大时可以将该模型近似看作是布朗运动。
由上可知,保险公司的盈余过程 描绘保险公司关于保险责任t时刻的收入支出过程是通过收入保费 ,支付再保保费 以及支付自留风险部分保险理赔费用 来衡量的,则盈余过程在很短的一段时间的变化量可被描述为:
(5)
2.1.2. 金融市场投资模型
本文所考虑的金融市场中理论资产配置由一个无风险资产和一个风险资产组成。其中,假设无风险资产在t时刻满足如下式(6):
(6)
令 ,而 表示无风险利率,一般其被假定为一个正的常数。
股票作为一种风险资产,是典型的风险投资工具,高风险高回报是其最为明显的特点。本文考虑的风险资产落实为股票,假设股票在时刻t的价格记为 ,其满足以下的GBM模型(7),即几何布朗运动:
(7)
其中, 是风险资产的瞬时收益率。假设 , 为一正常数,而 是标准布朗运动。
保险公司的整体财富过程 包括两个部分,一个部分是保险盈余部分,另一个部分则是金融投资部分。其中,盈余过程满足 过程,而投资部分则用式(6)中的无风险资产 和式(7)中风险资产 的组合来描述。
在任意时刻 记 是t时刻的策略,其中,设 是t时刻分出给再保公司保险责任的比例, 是t时刻全部资金中投资于风险资产的比例。策略 选定后设财富过程为 ,简记为 ,满足下面的随机微分方程:
(8)
初始条件, 。上式中涉及的布朗运动 和 是相互独立的。
现对 进行二次变差的处理,则
定义再保险–投资策略 是可允许的,若满足以下条件:
1) 是关于 可测的;
2)对任意的 ,有 ;
3) ;
4) 随机微分方程(8)中的控制 有唯一的强解。
令 ,当初始条件满足 时,令 表示所有可允许策略集。
2.1.3. 均值–方差问题
现实生活中,一部分保险投资者可能不是很愿意承担来自风险资产与保险业务的额外风险,他们更倾向于投资到较多的无风险资产与较少的保险业务上;而有一部分人可能会愿意承担上面的风险,而去投资更多的风险资产与保险业务。最优化问题一般会假定保险公司的决策者对风险保持厌恶的心理,但这一假设不能客观反映所有人对风险持有的态度,不同的风险态度对决策的影响亦不同。这里我们介绍一个对保险公司而言能够更好地管理风险的最优化问题。
记 为终值时刻T时,在策略 下,保险公司的财富。保险人希望能在所有可行策略中寻找到一个策略 ,使得 同时使下式(9)最小:
(9)
该问题称为均值–方差组合选择问题,即如下的描述:
定义均值–方差组合选择问题是以参数 为限制的随机最优化问题,目标函数也就是
(10)
定义 ,。
式(10)中 , 是给定 下的条件期望和条件方差。定义中的均值–方差组合选择问题对每一个都是可行的,当且仅当 。
2.2. 模型求解
在整篇论文中,我们将致力于解出 。在该部分中,我们引入伊藤公式。首先定义Ito process (伊藤过程):
定义
(11)
其中 服从标准布朗运动, 是常数。对 进行泰勒展开来求伊藤公式:
(12)
在二次项中,标准布朗运动的方差可求得为t,有 ,其余项为0。
由此,令 ,则:
下面将确定性策略与适应性策略进行对比:
1) 适应情形下的策略
针对式(8),则相应的对汉密尔顿–雅可比–贝尔曼(HJB)方程进行一定的推导,最终得到:
(13)
其中, 和 分别是对变量t和x的一阶偏导数, 是对变量x的二阶偏导数。通过目标泛函和值函数的关系,我们可以知道:
当选择最优策略 时的目标泛函等于值函数,可以证明通过值函数求解的控制就是希望得到的最优控制。这样就将一个最优控制问题,转化为求解(13)式中的HJB方程的问题。在(13)式中,包含控制 和 ,它们是函数而不是常数,且满足 ,。
这样,就得到式(13)关于 和 的一阶可导条件分别为:
最终可以求得适应策略下的最优再保险策略与风险投资比例的函数表达式为如下:
(14)
由于得到满足式(8)的问题的解析解是较为困难的,先拟设, ,很容易得到HJB方程如下改进形式:
(15)
注意值函数是二次函数,对应术语x,x2前的系数满足为零,则:
(16)
有着边界条件为 ,,。我们对最优策略的解的形式很感兴趣,令 ,代入式(16)可得:
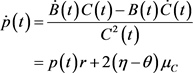
关于 ,
,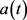 分别求导,且求解出
分别求导,且求解出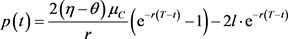 ,则
,则
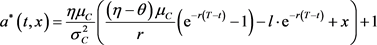
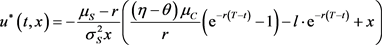
最后,我们要解决的问题即可变为求取最佳的。因此,我们必须计算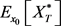 ,即最优投资与再保险策略下的预期终端财富。我们可以得到:
,即最优投资与再保险策略下的预期终端财富。我们可以得到:
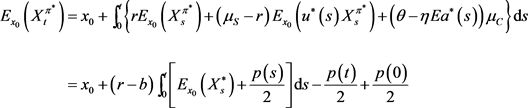
其中,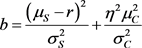 。下有:
。下有:
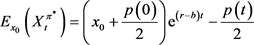
确定性策略中的再保险比例和投资数量,为能过有效的对比,我们采取了将适应下策略进行期望取值。
根据有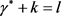 这一关系,则
这一关系,则
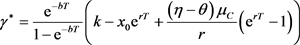
注意该情形下的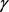 是与理赔的漂移率
是与理赔的漂移率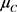 呈正相关关系,与再保费相对保费安全负载
呈正相关关系,与再保费相对保费安全负载 呈正相关趋势。
呈正相关趋势。
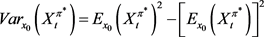
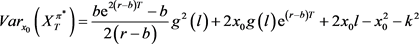
其中,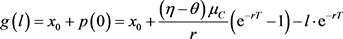 。
。
2) 确定情形下的策略
上一部分主要是介绍了适应性最优策略下的解析形式,我们假设现在投资策略必须预先确定,即财富过程中 是关于
是关于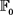 可测的,这意味着它是确定性的,只是时间t的函数。因此,保险公司的基金经理必须在
可测的,这意味着它是确定性的,只是时间t的函数。因此,保险公司的基金经理必须在 解释
解释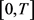 时的投资策略,而不使用关于过程演化的进一步知识,这看起来至少有时比自适应策略方程更现实些。一般情况下,管理基金者会激励这种只依赖时间的投资策略战略,因此对确定性策略的研究也就显得极为重要。
时的投资策略,而不使用关于过程演化的进一步知识,这看起来至少有时比自适应策略方程更现实些。一般情况下,管理基金者会激励这种只依赖时间的投资策略战略,因此对确定性策略的研究也就显得极为重要。
针对确定性的投资,这里我们需要对最优投资所涉及的参数含义进行一定的修改,可仍设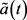 是确定初始投资
是确定初始投资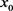 的再保险比例,而
的再保险比例,而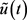 为最初投资为
为最初投资为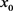 时所确定的投资数量,则相应的财富过程
时所确定的投资数量,则相应的财富过程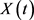 如下表示:
如下表示:
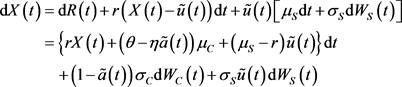
首先,我们定义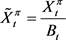 为贴现财富过程,此下定义的过程在另一个测度Q下进行的,但是可以找
为贴现财富过程,此下定义的过程在另一个测度Q下进行的,但是可以找
到P和Q之间的联系,本文中先不讨论它们之间的关系。
下面这样做可以消除t时刻财富过程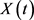 对所确定的策略的影响,则有:
对所确定的策略的影响,则有:
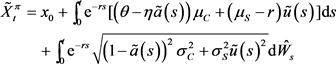
其中, 是将两个布朗运动信息整合起来而构建的一个新的布朗运动,可令
是将两个布朗运动信息整合起来而构建的一个新的布朗运动,可令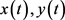 为
为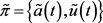 上的函数,其中:
上的函数,其中:
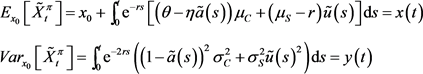
利用拉格朗日算子可得:

该问题的值函数即可满足如下式:
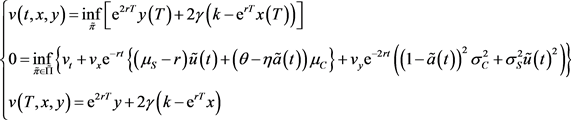 (17)
(17)
现可拟设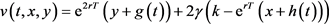 ,有
,有 。
。
我们有
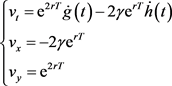 (18)
(18)
分别对式(17)中关于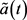 ,
,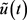 求一阶导数,则最终的最优策略为:
求一阶导数,则最终的最优策略为:
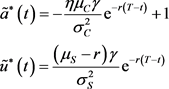 (19)
(19)
计算得到
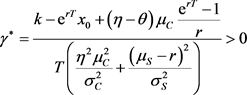 (20)
(20)
将上式中的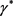 代入到式(17)中。最终可求得确定情形下的均值–方差的有效策略为:
代入到式(17)中。最终可求得确定情形下的均值–方差的有效策略为:
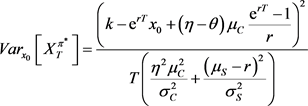
上文已介绍了最优投资与再保险问题需要用到的模型,且对终端时间确定的适应性策略与确定性策略皆作了一定的推导与分析。事实上,在确定性下的再保险与金融投资策略中,策略仅作为时间t的函数;而适应性策略或多或少会依赖于t时刻的财富,相较于确定性的策略更为复杂。
3. 结论
根据所做的数值模拟,如图1所示,对比发现适应性策略效果较差于确定性策略,而改变风险资产的收益率,波动率,初始价格对风险资产(股票)的影响如下图2所示。且根据所做的研究,可知:给定其他条件下,最优投资策略与风险资产预期收益率是呈现正相关趋势的。当风险资产预期回报率增大时,保险公司会增加风险资产的财富配置,以获取更高的回报。相反,当风险资产收益率下降时,保险公司会减少分配于风险资产的比例。
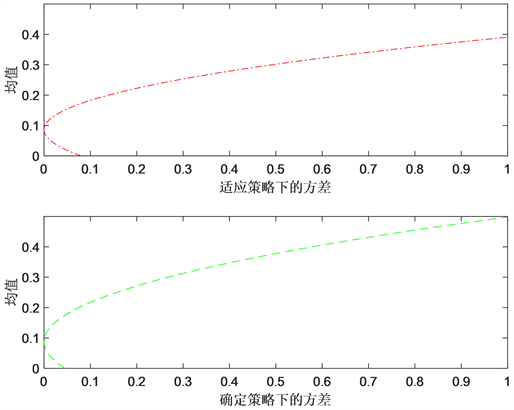
Figure 1. Comparative analysis of deterministic and adaptive effects
图1. 确定性与适应性效果对比

Figure 2. Risky assets under each parameter change over time
图2. 各参数下风险资产随时间变化
若给定其他条件,当高波动率发生时,市场的不稳定性很高,表明企业的风险管理资产在产生经济收益时,不确定性也很高。在这种情形下,为了控制风险,保险公司会减少在风险资产上的配置。相反,风险资产的波动率越低,保险公司所投资的风险资产越多。
给定其他条件下,再保险费率增大时,保险公司会采纳较高的保险发展业务的自留水平,同时采取较低的再保险比例。相反,当再保险费率降低时,保险公司会采取更高的再保险比例,而降低保险业务的自留比例。
致谢
在论文完结之际,本人特在此表示衷心的感谢:指导老师对论文阅读写作的引领,甚至于每一细节方面的指导。感谢导师对论文的指导,也感谢室友对项目的支持。
基金项目
国家级大学生创新创业训练计划资助202010497050。
文章引用
蔡 畅,刘方盈. 均值方差准则下的投资与再保险对比研究
Comparative Study of Investment and Reinsurance under the Mean-Variance Criterion[J]. 应用数学进展, 2021, 10(06): 2060-2072. https://doi.org/10.12677/AAM.2021.106216
参考文献
- 1. Cao, Y.S. and Wan, N.Q. (2009) Optimal Proportional Reinsurance and Investment Based on Hamilton-Jacobi-Bell- man Equation. Insurance: Mathematics and Economics, 45, 157-162. https://doi.org/10.1016/j.insmatheco.2009.05.006
- 2. 林祥, 李娜. 索赔次数为复合Poisson-Geometric过程下的破产概率和最优投资和再保险策略[J]. 应用数学, 2011(1): 174-180.
- 3. 桂有利. 具有模型不确定性的最优投资和再保险策略[D]: [硕士学位论文]. 长沙: 中南大学, 2009.
- 4. 王宁. 模型不确定性及博弈框架下最优投资与再保险策略的相关研究[D]: [博士学位论文]. 上海: 华东师范大学, 2020.
- 5. Chen, Z. and Yang, P. (2020) Robust Optimal Reinsurance-Investment Strategy with Price Jumps and Correlated Claims. Insurance: Mathematics and Economics, 92, 27-46. https://doi.org/10.1016/j.insmatheco.2020.03.001
- 6. 李悦. 在不可观测模式转换情况下的最优投资和再保险策略研究[D]: [硕士学位论文]. 天津: 天津财经大学, 2018.
- 7. 杨鹏. 均值-方差准则下CEV模型的最优投资和再保险[J]. 系统科学与数学, 2014, 34(9): 1100-1107.
- 8. Zhang, Q. and Chen, P. (2018) Time-Consistent Mean-Variance Proportional Reinsurance and Investment Problem in a Defaultable Market. Optimization, 67, 683-699. https://doi.org/10.1080/02331934.2018.1434650
- 9. 罗琰, 杨招军. 保险公司最优投资及再保险策略[J]. 财经理论与实践, 2009, 30(3): 31-34.
- 10. Bäuerle, N. and Rieder, U. (2013) Optimal Deterministic Investment Strategies for Insurers. Risks, 1, 101-118. https://doi.org/10.3390/risks1030101
- 11. Yao, H., Li, Z. and Duan, L. (2016) Multi-Period Mean-Variance Portfolio Selection with Stochastic Interest Rate and Uncontrollable Liability. European Journal of Operational Research, 252, 837-851. https://doi.org/10.1016/j.ejor.2016.01.049
- 12. Zeng, Y. and Li, Z.F. (2011) Optimal Time-Consistent Investment and Reinsurance Policies for Mean-Variance Insurers. Insurance: Mathematics and Economics, 49, 145-154. https://doi.org/10.1016/j.insmatheco.2011.01.001
- 13. Guo, W.J. (2014) Optimal Portfolio Choice for an Insurer with Loss Aversion. Insurance Mathematics & Economics, 58, 217-222. https://doi.org/10.1016/j.insmatheco.2014.07.004
附录
% 代码.调节参数对问题进行分析
%EM Euler-Maruyama method on linear SDE
% SDE is dX = lambda*X dt + mu*X dW,X(0) = Xzero,
randn('state',100)%调节参数来分析变化
lambda1=2; mu1=1; Xzero1=1;% problem parameters
lambda2=2; mu2=0.5; Xzero2=1;% 波动率
lambda3=2.5; mu3=1; Xzero3=1;% 收益率
lambda4=2; mu4=1; Xzero4=2;% 初始价格
T= 1;N=100; dt = 1/N; dW = sqrt(dt)*randn(1,N);% Brovnian increments
W=cumsum(dW) ; % discretized Brovnian path
Xtrue1 = Xzero1*((lambda1-0.5*mu1^2)*((dt:dt:T))+mu1*W);
Xtrue2 = Xzero2*((lambda2-0.5*mu2^2)*((dt:dt:T))+mu2*W);
Xtrue3 = Xzero3*((lambda3-0.5*mu3^2)*((dt:dt:T))+mu3*W);
Xtrue4 = Xzero4*((lambda4-0.5*mu4^2)*((dt:dt:T))+mu4*W);
figure;
subplot(2,2,1);
plot((0:dt:T),[Xzero1,Xtrue1], 'g-');title('风险资产原始设定');
subplot(2,2,2);
plot((0:dt:T),[Xzero2,Xtrue2], 'y-');title('风险资产波动率');
subplot(2,2,3);
plot((0:dt:T),[Xzero3,Xtrue3], 'b-');title('风险资产收益率');
subplot(2,2,4);
plot((0:dt:T),[Xzero4,Xtrue4], 'r-');title('风险资产初始价格');
NOTES
*通讯作者。