Pure Mathematics
Vol.06 No.03(2016), Article ID:17689,11
pages
10.12677/PM.2016.63040
The C1 Invariant Curve of Lyness Type Difference Equations
Miaoqiao Pan, Ruiqi Chen, Zongzhao Mo, Fuge Pan, Yezhi Li, Ying Zhang
School of Mathematics and Computational Science, Lingnan Normal University, Zhanjiang Guangdong

Received: May 6th, 2016; accepted: May 20th, 2016; published: May 27th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, by using the Schauder fixed point theorem and Banach fixed point theorem, also the related properties of the compact convex subset, the existence, uniqueness; stability and retention property of the C1 invariant curves of Lyness type difference equations are researched.
Keywords:Lyness Type Difference Equations, Invariant Curves, Existence, Uniqueness, Stability, Retention Property

关于Lyness型差分方程的C1不变曲线
潘妙巧,陈瑞琪,莫宗赵,潘富格,李叶芷,张颖
岭南师范学院数学与计算科学学院,广东 湛江

收稿日期:2016年5月6日;录用日期:2016年5月20日;发布日期:2016年5月27日

摘 要
本文利用Schauder不动点定理、Banach不动点定理及紧凸子集的相关性质研究了关于Lyness型差分方程的C1不变曲线的存在性、唯一性、稳定性及保向性。
关键词 :Lyness型差分方程,不变曲线,存在性,唯一性,稳定性,保向性

1. 引言
许多物理、力学、生物以及天文学的数学模型都是离散的迭代过程描述的,动力系统的许多问题都可以化为泛函方程,它具有广泛的现实意义和应用背景,一直受到科学家们的广泛关注。20世纪以来,众多学者已研究若干迭代函数方程的不变曲线问题,比如Wagner,Nabeya,Dhombres在研究某类不变曲线问题时,最终归结到讨论方程

的解。近年来,C. T. Ng和张伟年 [1] 用迭代方程的方法研究了一类二阶具有逐段常数的变时滞泛函微分方程

的不变曲线问题。1999年,李继彬等 [2] 研究了推广的Lyness方程的不变曲线问题,2001年,贺天兰 [3] 研究了一类差分方程的不变曲线分枝,2012年,陈华春等 [4] 研究了一类非线性差分方程的不变曲线。
本文将在他们的基础上,利用嵌入流的相关知识定性研究Lyness型差分方程
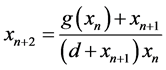 (1.1)
(1.1)
的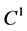 不变曲线问题,将该差分方程连续化,考虑对应的二阶非线性迭代泛函方程
不变曲线问题,将该差分方程连续化,考虑对应的二阶非线性迭代泛函方程
 (1.2)
(1.2)
其中

然后利用Schauder不动点定理、Banach不动点定理及紧凸子集的相关性质获得了该差分方程存在唯一的 不变曲线
不变曲线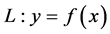 的相关条件,并给出了其保向性,进而实例给予验证。
的相关条件,并给出了其保向性,进而实例给予验证。
2. 预备知识
本文所涉及的相关的定义以及引理:
定义2.1 [4] :设实平面上的变换T:
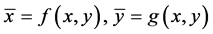
或

而若曲线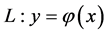 经
经 变为另一曲线
变为另一曲线 就记为
就记为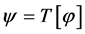 。
。
若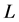 经
经 变到自身,即
变到自身,即 ,则称
,则称 是
是 的不变曲线,此时,也有
的不变曲线,此时,也有 ,从而得到迭代函数方程
,从而得到迭代函数方程

这称为不变曲线的方程。
定义2.2 [5] :Banach不动点定理(压缩映射原理)设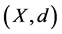 是完备距离空间,
是完备距离空间,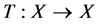 是理压缩映射,则
是理压缩映射,则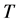 有唯一不动点,即存在唯一的
有唯一不动点,即存在唯一的 使得
使得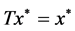 。
。
定义2.3 [5] :Schauder不动点定理:设 是巴拿赫空间中的紧凸集,那么
是巴拿赫空间中的紧凸集,那么 到自身的每个连续映射都至少有一个不动点。
到自身的每个连续映射都至少有一个不动点。
记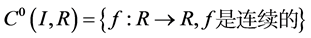 ,显然
,显然 是一个Banach空间,其中对
是一个Banach空间,其中对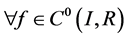 ,
,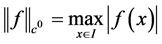 ,且
,且 。
。
又记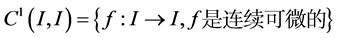 ,易见
,易见 是完备的Banach空间,其中对
是完备的Banach空间,其中对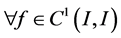 ,
, 。
。
定义2.4 [1] :如果存在自然数 ,使得
,使得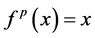 ,则称
,则称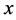 为
为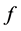 的周期点。满足这一关系的最小自然数
的周期点。满足这一关系的最小自然数 称为
称为 的周期,这时
的周期,这时

直接称 为p-周期点。特别地,当
为p-周期点。特别地,当 时,
时, ,称
,称 为
为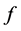 的不动点。
的不动点。
引理2.1:假设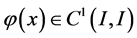 并且
并且

其中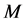 和
和 是正数,则对
是正数,则对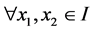 ,则有
,则有
(i) 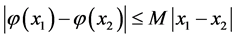
(ii) 
(iii) 
(iv) 
证明参考文献 [6] 。
引理2.2:在引理2.1的条件下,还有
(i) 
(ii) 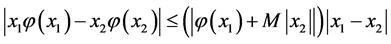
(iii) 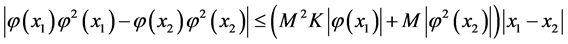
(iv) 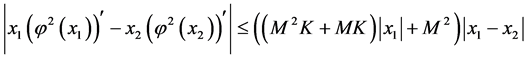
(v) 
证明:在引理2.1的条件下,有
对 ,由条件,得
,由条件,得
(i) 
(ii) 
(iii) 
(iv) 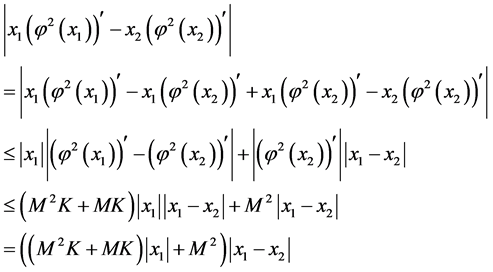
(v) 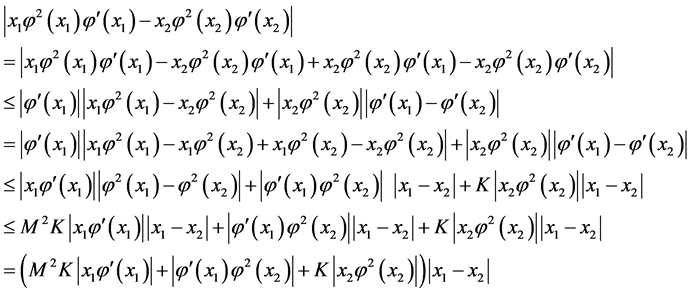
3. 主要结果
记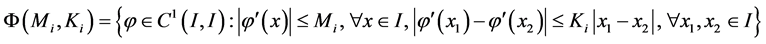
任取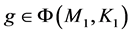 ,
, 。
。
定理3.1 (存在性)若存在正的常数 满足
满足
(E1) 
(E2) 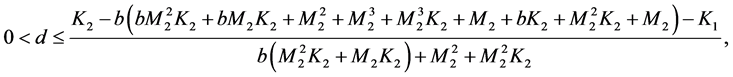

则方程 有解
有解 。
。
证明:构造算子

且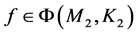 ,
, 是连续可微的。
是连续可微的。
接下来分三步进行证明:
(1) 算子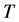 是自同胚的
是自同胚的
对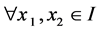 ,有:
,有:

由(E1)得
又

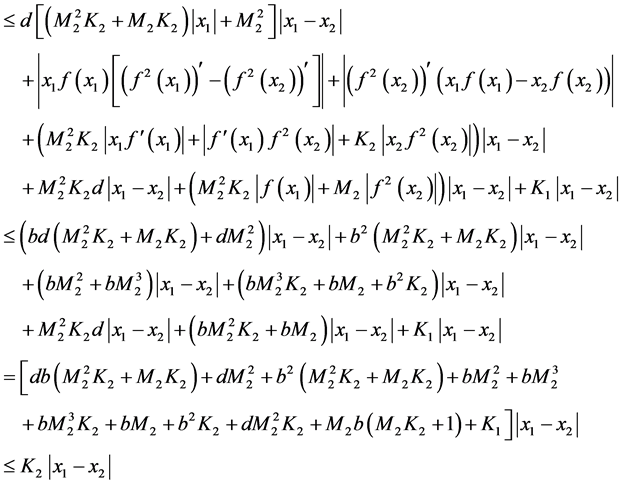
由(E2)得 。
。
由上可知算子 是一个自同胚映射。
是一个自同胚映射。
(2)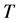 在范数
在范数 下是连续的
下是连续的

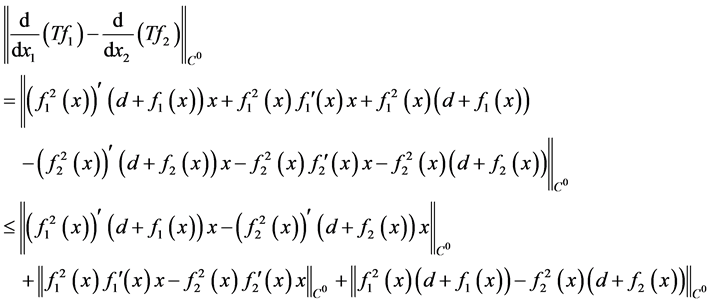
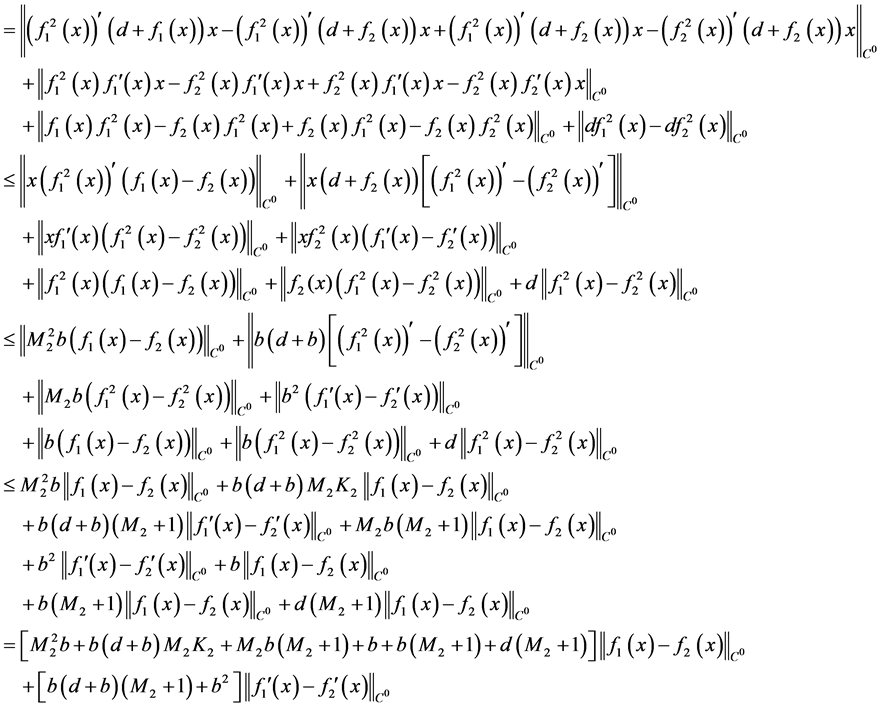
即
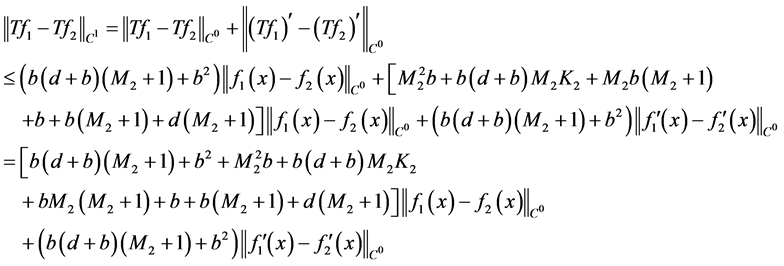
令
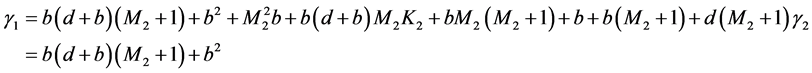
取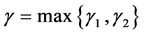 ,那么就有
,那么就有
 (3.11)
(3.11)
由上证得算子 在范数
在范数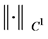 下是连续的。
下是连续的。
(3) 类似于文献 [6] , 是
是 一个紧凸子集。
一个紧凸子集。
综上,由Schauder不动点定理可知,存在一个函数满足
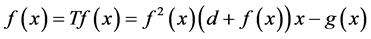
因为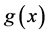 是非线性的,所以解
是非线性的,所以解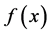 也是非线性的,则
也是非线性的,则 在
在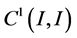 上有不变曲面。
上有不变曲面。
亦则差分方程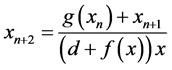 存在不变曲线。
存在不变曲线。
定理3.2 (唯一性)若定理3.1条件(E1)和(E2)满足, ,同时满足以下条件
,同时满足以下条件
(E3):
则方程 的解
的解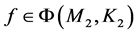 唯一的。
唯一的。
证明:由(3.11)可知 ,且有
,且有 ,则
,则 是
是 上的一个压缩映射,又因为
上的一个压缩映射,又因为 是Banach空间
是Banach空间 的一个闭子集,由Banach不动点定理可知,
的一个闭子集,由Banach不动点定理可知, 在
在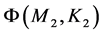 内必有唯一的不动点
内必有唯一的不动点 ,则不变曲线是唯一的,亦则差分方程
,则不变曲线是唯一的,亦则差分方程 存在唯一的不变曲线。
存在唯一的不变曲线。
定理3.3 (稳定性)设定理3.2中的条件成立,则在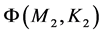 中方程(1.2)的解是连续依赖给定的函数
中方程(1.2)的解是连续依赖给定的函数 。
。
证明:对于 ,由定理3.1及定理3.2可以分别得出存在唯一的函数
,由定理3.1及定理3.2可以分别得出存在唯一的函数 ,证明使得
,证明使得 。
。
有


因为 ,有
,有
即 。
。
故方程(1.2)的解是连续依赖于给定的函数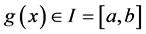 。
。
定理3.4 (保向性)设定理3.2中的条件成立,对于任意 ,若存在
,若存在 ,且满足
,且满足

则 且
且 为上保向同胚。
为上保向同胚。
证明:对 ,令
,令 ,则有,
,则有,


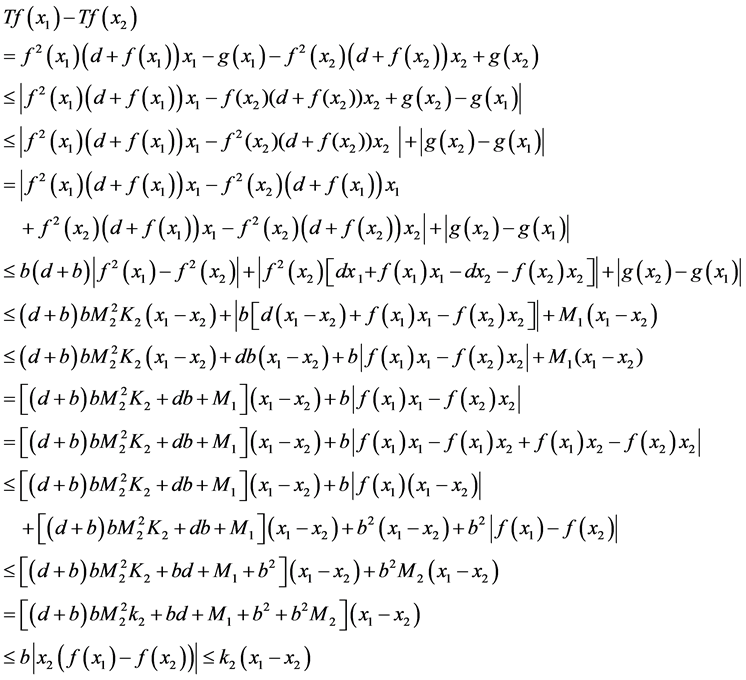

令 ,
,
由条件有 ,即
,即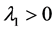 ,
,
故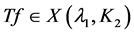 且
且 为上保向同胚。
为上保向同胚。
4. 举例应用
[例]设 ,
, ,
,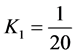 ,
,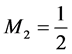 ,
,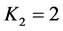 ,
,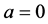 ,
,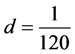 ,且
,且 是连续函数,且有
是连续函数,且有 ,
, ,则方程
,则方程 在
在 内有唯一的解,即差分方程
内有唯一的解,即差分方程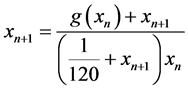 在
在 上有唯一的不变曲线。
上有唯一的不变曲线。
基金项目
广东省大学生科技创新重点培育项目,编号:pdjh2016a0301;岭南师范学院2015年度大学生创新创业训练计划项目;2015年度广东省大学生创新创业训练计划项目,编号:201510579292。
文章引用
潘妙巧,陈瑞琪,莫宗赵,潘富格,李叶芷,张 颖. 关于Lyness型差分方程的C1不变曲线
The C1 Invariant Curve of Lyness Type Difference Equations[J]. 理论数学, 2016, 06(03): 261-271. http://dx.doi.org/10.12677/PM.2016.63040
参考文献 (References)
- 1. 张景中, 杨路, 张伟年. 迭代方程与嵌入流[M]. 上海: 上海科技教育出版社, 1998.
- 2. Li, J.-B. and Liu, Z.-R. (1999) Invariant Curves of the Generalized Lyness Equation. International Journal of Bifurcation and Chaos, 9, 1143-1450.
- 3. 贺天兰. 一类差分方程的不变曲线分枝[J]. 应用数学和力学, 2001, 22(9): 988-996.
- 4. 陈华春, 陈超霞, 李华. 关于一类非线性差分方程的不变曲线[J]. 湛江师范学院学报, 2012, 33(6): 38-43.
- 5. 郭大钧. 非线性泛函分析[M]. 济南: 山东科学技术出版社, 2001.
- 6. 林雪梅, 黄上梅, 黄海敏, 等. 关于Feigenbaum型泛函方程的C1解[J]. 湛江师范学院学报, 2012, 32(3): 33-37.