Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30358
,
10
pages
10.12677/PM.2019.93052
Fixed Point Theorems for a Generalized Meir-Keeler-Rational Contraction in Partial
-Generalized Metric Spaces
Xiaohui Wang, Peisheng Ji, Fangyuan Dong
School of Mathematics and statistics, Qingdao University, Qingdao Shandong

Received: Apr. 26th, 2019; accepted: May 6th, 2019; published: May 22nd, 2019

ABSTRACT
In this paper, we consider the fixed points of generalized Meir-Keeler-Rational contractions in the context of partial
-generalized metric spaces. Our results generalize several known ones in literature.
Keywords:Meir-Keeler-Rational Contraction, Partial
-Generalized Metric Space, Fixed Points

偏
-度量空间中有关Meir-Keeler-Rational型 映射的不动点理论
王小卉,纪培胜,董芳远
青岛大学,数学与统计学院,山东 青岛

收稿日期:2019年4月26日;录用日期:2019年5月6日;发布日期:2019年5月22日

摘 要
本文主要介绍了偏
-度量空间中有关Meir-Keeler-Rational型映射的不动点定理,我们的结果推广了以往论文中的一些结论。
关键词 :Meir-Keeler-Rational型映射,偏
-度量空间,不动点

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Banach [1] 引入的Banach收缩原理是数学分析中最重要的结果之一,它是数学许多分支中应用最广泛的不动点理论,并在许多不同的方向上被进行了推广。其中一方面推广涉及度量空间的各种推广,且在新的框架中得到不动点的结果,例如,在b-度量空间、广义度量空间和偏序度量空间中发表了一些关于这个主题的论文。2014年,Shukla [2] 推广了b-度量空间和偏序度量空间,定义了偏b-度量空间的概念。Mitrovic和Radenovic [3] 推广了
-度量空间 [4] ,引入了
-度量空间的概念。Abdullahi和Kumam [5] 推广了偏序度量空间和
-度量空间,定义了偏
-度量空间,且在其中建立了不动点理论。他们在论文中提出了一些开放型问题:是否可以类似的在推广的
-度量空间,
-度量空间,偏
-度量空间中证明Chatterjee型压缩、Hardy-Roger型压缩、Ciric型压缩和Suzuki型压缩的不动点问题。
另一方面是对压缩条件进行推广。Meir-Keeler [6] 采用了一种不同的方法来概括受到广泛关注的Banach收缩原理。准确地说,他们取得了以下令人印象深刻的结果。
定理1.1: [6] 假设映射A是完备度量空间
上的一个自映射,且满足下述条件:对给定的
,存在
,对于任意的
,有
这个结果随后被推广到很多方面。例如Jachymski [7] 提出了一些等同于Meir-Keeler类型条件的条件,并建立了一个完善的不动点理论,该理论将Meir-Keeler的理论广泛化。
定理1.2: [7] 假设映射A是完备度量空间
上的一个自映射,且满足下述条件:
1) 对给定的
,存在
,对于任意的
,有
其中
;
2) 对任意的
,且
,
若A是连续的则A有唯一的不动点。
本文中我们将在偏
-度量空间中建立推广的Meir-Keeler型映射的不动点理论,并且给出这一理论的一些直接的结果。
2. 预备知识
从现在开始,我们用
分别代表正整数,实数,正实数,非负实数。下面我们回顾一下偏
-度量空间的定义。
定义2.1: [5] 令X是非空集合,映射
,,若对于任意的
,存在互不相同的元素
,且它们与x和y是互异的,有下列条件成立:
1)
当且仅当
;
2)
;
3)
;
4) 存在
且
,有
(偏
-不等式)。
则d称为X上的偏
-距离,
称为偏
-度量空间,且系数
。
注1 [5] 在偏
-度量空间
中,若对
,有
,则
。反之不一定成立。
注2 [5]
1) 偏
-度量空间是偏度量空间 [8] ;
2) 偏
-度量空间是偏b-度量空间,系数
[2] ;
3) 偏
-度量空间是偏矩形度量空间 [9] ;
4) 偏
-度量空间是偏矩形b-度量空间,系数
;
5) 偏
-度量空间是偏
-度量空间。
定义2.2:令X是一个非空集合,映射
,。若对任意的
,存在互不相同的元素
,且它们与x和y是互异的,有下列条件成立:
1)
当且仅当
;
2)
;
3)
;
4)
(偏
-不等式)。
则d称为X上的偏
-距离。
称为偏 -度量空间。
-度量空间。
定义2.3: [5] 令
是偏
-度量空间,数列
,且
。则
1) 若
,则数列
称为X中的收敛列,且收敛于x。x称为数列
的极限,记为
,或
,。
2) 若
存在,则数列
称为X中的柯西列。
3) 若对于X中的每个柯西列
,存在
,且
,则
称为完备的偏
-度量空间。
在 [5] 中我们给出了一些例子来说明偏
-度量空间上的拓扑与推广的度量空间上的拓扑是不相容的 [10] 。因此,我们在偏
-度量空间中定义了连续性。
定义2.4:若当
, 时,有
,则称映射T是连续的。
Samet等人 [11] 通过定义
-收缩映射和
-容许映射给出了一个有趣的结果,同时也推广了Banach收缩原理。
定义2.5: [11] 令T是集合X上的一个自映射,函数
,我们称T是
-容许映射,若对
,下列条件成立:
定义2.6: [12] 令X是非空集合,映射
,函数
。我们称T是三角
-容许映射,若有下列条件成立:
1) 对任意
,且
,有
成立。
2) 对任意的
,且
,,有
成立。
若对所有的
,有
成立,我们称
具有反身性。
引理2.1: [12] 令T是三角
-容许映射。假设存在
,且
。通过如下方式来定义数列
:
。则对所有的
,且
,有
成立。
下面的引理将用于证明我们的主要结论。
引理2.2:令
是偏
-度量空间,数列
是X中的柯西列,当
时,有
,且
。则数列
至多收敛于一个点。
证明:假设
是数列
的两个极限,且
由偏
-不等式,我们有
因为
,我们得到
。由偏
-推广度量空间的定义,有
。
引理2.3:令
是非负数列。若
,,则
。
在本文中,我们用
代表映射T的不动点集合。
3. 主要结论
在这一节中,我们将在完备的偏
-度量空间中来证明我们的结论。
定理3.1:令
是完备的偏
-度量空间,函数
,映射
。假设下列条件成立:
1) 对所有的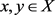 ,且
,有
,且
,有
(3.1)
其中
;
2) 对任意的
,存在
,对所有的
,有
,
; (3.2)
3) T是三角
-容许映射,且
具有反身性;
4) 存在
,有
成立;
5) T是连续的。
则T有唯一的不动点u,且
收敛于u。更进一步,若对所有的
,有
,则T在X中有唯一的不动点。
证明:令
且满足
。我们通过下列方式来构造数列
:
,。若对某个
,有
,则
是T的不动点。在接下来的证明中,我们假设对所有的
,。因为T是
-容许映射,对所有的
,,我们有
(3.3)
1) 我们首先证明
。
在(3.1)中令
,,我们得到
(3.4)
其中
(3.5)
利用(3.4)和(3.5),对所有的
,我们得到
(3.6)
因此
是递减数列。故存在
,使
。明显地,对于所有的
,。若
,令
,存在
,对所有的
,有
,
(3.7)
因为对于所有的
,,,则存在
,对所有的
,有
由(3.7),对所有的
,我们得到
,这与
, 是矛盾的。因此得到
。因此
(3.8)
2) 下面我们证明对所有的
,有
。假设若对某一
,有
成立,因此我们得到
。由(3.6),得到
,矛盾。因此,对任意
,。
3) 接下来证明,对任意的
,且
,有
成立。
因为
,对任意的
,我们可以假设
。在(3.1)中,令
,。因
,,我们得到
(3.9)
其中
因为数列
是递减的,且对所有的
,有
,故得到
(3.10)
由(3.9)和(3.10),得到
(3.11)
令
,,故
因为
,因此对任意的
,得到
。故数列
是递减的,假设它收敛于某一
。因为
,由引理2.3得到
若
,因为
,,接下来,我们假设
,,即
,。
令
,存在
,对任意的
,有
,
(3.12)
因为对所有的
,,且
,则存在
,对
,有
由(3.12),对所有的
,,这与
, 是矛盾的。故
。即
(3.13)
4) 下面我们证明
。相反地,我们假设
不收敛于0,选取子列
,存在
, 是使下列式子成立的最小指标
,
(3.14)
由定理3.1条件(2)知,存在
,对任意的
,
,
(3.15)
显然地,(3.15)式中用
来代替
,(3.15)仍成立。因为
,,则存在
,对所有
,有
(3.16)
对
,由偏
-不等式,有
即
。
因为
,,即能推得存在
,有
(3.17)
其中
(3.18)
利用定理3.1条件(2),我们有
。然而,由(3.15)~(3.18)知
这与已知的矛盾。故
,即
是柯西列。因为
是完备的,所以存在
,使得
5) 假设T是连续的,下面我们证明u是T的不动点。因为T是连续的,则
因为对于
,数列
满足
,我们可以假设每一
与
都是不同的。考虑
因
,得到
。因此
(3.19)
假设u不是T的不动点,即
,则
因为
具有反身性,由(3.1),
,我们得到
这与(3.19)是矛盾的。即u是T的不动点。
6) 最后,我们证明T的不动点是唯一的。假设
是T的两个不动点,且
。则由假设
。
所以由(3.1)式,
,得到
其中
即
矛盾。因此
。
推论3.2:令
是完备的偏
-度量空间。映射
是单调的,且满足下列条件:
1) 对任意的
,且
,若
,则有
,其中
;
2) 对任意的
,存在
,且对任意的
,有
,
;
3) 存在
,满足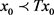 ;
;
4) T是连续的。
则T存在不动点u且
收敛于u。更进一步,若对任意的
,我们有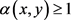 ,则T在X中存在唯一的不动点。
,则T在X中存在唯一的不动点。
证明:定义
,且
显然地,由定理3.1,T存在不动点。
致 谢
在论文完成之际,我要特别感谢纪培胜老师的热情关怀和悉心指导,无论是在论文的选题、构思和资料的收集方面,还是在论文的研究方法以及成文定稿方面,纪老师都给予了无私的帮助,在此表示真诚的感谢和深深的谢意。在论文的写作过程中,也得到了董芳远同学的宝贵建议,在此一并致以诚挚的谢意。最后,还要感谢山东省自然科学基金资助项目对本论文的支持。
基金项目
山东省自然科学基金资助项目(ZR2016AM05)。
文章引用
王小卉,纪培胜,董芳远. 偏v-度量空间中有关Meir-Keeler-Rational型映射的不动点理论
Fixed Point Theorems for a Generalized Me-ir-Keeler-Rational Contraction in Partial v-Generalized Metric Spaces[J]. 理论数学, 2019, 09(03): 393-402. https://doi.org/10.12677/PM.2019.93052
参考文献
- 1. Banach, S. (1922) Sur les operations dans les ensembles abstraits et leur application aux equations integrals. Fundamenta Mathematicae, 20, 133-181.
https://doi.org/10.4064/fm-3-1-133-181
- 2. Shukla, S. (2014) Partial b-Metric Spaces and Fixed Point Theorems. Mediterranean Journal of Mathematics, 11, 703-711.
https://doi.org/10.1007/s00009-013-0327-4
- 3. Mitrovic, Z.D. and Radenovic, S. (2017) The Banach and Reich Contractions in -Metric Spaces. Fixed Point Theory and Applications, 19, 3087-3095.
https://doi.org/10.1007/s11784-017-0469-2
- 4. Branciari, A. (2000) A Fixed Point Theorem of Banach-Caccioppoli Type on a Class of Generalized Metric Spaces. Publicationes Mathematicae, 57, 31-37.
- 5. Abdullahi, M.S. and Kumam, P. (2018) Partial -Metric Spaces and Fixed Point Theorems. Fixed Point Theory and Applications, 20, 113.
https://doi.org/10.1007/s11784-018-0591-9
- 6. Meir, A. and Keeler, E. (1969) A Theorem on Contraction Mappings. Journal of Mathematical Analysis & Applications, 28, 326-329.
https://doi.org/10.1016/0022-247x(69)90031-6
- 7. Jachymski, J. (1995) Equivalent Conditions and the Meir-Keeler Type Theorems. Journal of Mathematical Analysis & Applications, 194, 293-303.
https://doi.org/10.1006/jmaa.1995.1299
- 8. Mattehews, S.G. (1994) Partial Metric Topology. Annals of the New York Academy of Sciences, 728, 183-197.
- 9. Shukla, S. (2014) Partial Rectangular Metric Spaces and Fixed Point Theorems. The Scientific World Journal, 2014, Article ID: 756298.
https://doi.org/10.1155/2014/756298
- 10. Suzuki, T. (2014) Generalized Metric Spaces Do Not Have the Compatible Topology. Abstract and Applied Analysis, 2014, Article ID: 458098.
https://doi.org/10.1155/2014/458098
- 11. Samet, B., Vetro, C. and Vetro, P. (2012) Fixed Point Theorems for -Contractive Type Mappings. Nonlinear Analysis, 75, 2154-2165.
https://doi.org/10.1016/j.na.2011.10.014
- 12. Vahid, P., Nawab, H. and Zoran, K. (2016) Generalized Wardowski Type Fixed Point Theorems via -Admissable FG-Contractions in b-Metric Spaces. Acta Mathematica Scientia, 5, 1445-1456.
https://doi.org/10.1016/s0252-9602(16)30080-7








 -度量空间。
-度量空间。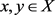 ,且
,有
,且
,有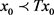 ;
;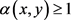 ,则T在X中存在唯一的不动点。
,则T在X中存在唯一的不动点。