青海民族大学数学与统计学院，青海 西宁

收稿日期：2022年11月27日；录用日期：2022年12月23日；发布日期：2022年12月30日

摘要

一个非完全连通图G的毁裂度定义为 $r\left(G\right)=max\left\{\omega \left(G-X\right)-\left|X\right|-\tau \left(G-X\right):X\subset V\left(G\right),\omega \left(G-X\right)>1\right\}$，其中 $\omega \left(G-X\right)$ 为 $G-X$ 的分支数， $\tau \left(G-X\right)$ 为 $G-X$ 最大分支的阶数。作为网络抗毁性参数之一，毁裂度 $r\left(G\right)$ 既能反映网络图G的破坏难度，又可反映破坏程度。在某种程度上，它代表了破坏网络所需的工作和破坏网络的严重程度之间的平衡。在本文中，我们确定了蝴蝶网络与增广蝴蝶网络的毁裂度。

关键词

毁裂度，蝴蝶网络，网络结构

Research on Invulnerability of Butterfly Network

Tingyi Zhu

School of Mathematics and Statistics, Qinghai University for Nationalities, Xining Qinghai

Received: Nov. 27^th, 2022; accepted: Dec. 23^rd, 2022; published: Dec. 30^th, 2022

ABSTRACT

The destruction degree of an incompletely connected graph G is defined as $r\left(G\right)=max\left\{\omega \left(G-X\right)-\left|X\right|-\tau \left(G-X\right):X\subset V\left(G\right),\omega \left(G-X\right)>1\right\}$, where $\omega \left(G-X\right)$ is the number of branches of $G-X$, and $\tau \left(G-X\right)$ is the order of the largest branch of $G-X$. As one of the parameters of network invulnerability, the degree of destruction $r\left(G\right)$ can reflect the network. The damage difficulty of graph G can reflect the degree of damage. To some extent, it represents the balance between the work required to destroy the network and the severity of the damage to the network. In this paper, we determine the butterfly network and augmented disintegration of butterfly network.

Keywords:Destruction Degree, Butterfly Network, Network Structure

Copyright © 2022 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

设G是一个连通图，其顶点集为 $V\left(G\right)$ 和边集 $E\left(G\right)$。通常用图G代表一网络拓扑结构，人们通过对图G的连通性讨论来研究网络结构的抗毁性。连通度、坚韧度、完整度、离散数、粘连度、毁裂度等参数均被引入刻画图的连通性，其中粘连度和毁裂度因考虑维度全面而备受学界关注，关于这两个参数的研究已有丰富结果，见文献 [1] [2] 和 [3]。

对于连通图G，如果 $G-X$ 不连通，那么顶点子集X称为图G的点割集。对于点割集X，我们分别用 $\omega \left(G-X\right)$ 和 $\tau \left(G-X\right)$ 表示 $G-X$ 中连通分支的个数和最大连通分支的阶数，并定义 $Sc\left(X\right)=\omega \left(G-X\right)-\left|X\right|-\tau \left(G-X\right)$。基于这些约定，非完全连通图G的毁裂度定义为 $r\left(G\right)=\max \left\{Sc\left(X\right):X\subset V\left(G\right),\omega \left(G-X\right)>1\right\}$。

如果 $Sc\left(X\right)=r\left(G\right)$，我们称点集X为G的r-集。因为毁裂度既能够衡量破坏网络所需的工作量，又能刻画网络的破坏程度，所以常被用来作为刻画网络抗毁性的重要指标。本文中没有定义的术语和符号见 [4]。

蝴蝶网络是并行分布式系统拓扑结构，它们在结构上具有良好的对称性 [5]。在并行分布式系统中，互联网络拓扑结构决定性能。蝴蝶网络作为对称互联网络模型，多年来在拓扑结构代数学图论中是重要的研究对象 [6]。

2. 蝴蝶网络的毁裂度

定义2.1. 设 $n>1$ 是一个整数。n维蝴蝶网络记为 $BF\left(n\right)$，其顶点集 $V=\left\{\left(i,x\right)\right\}$，其中i是非负整数且 $0\le i\le n$，$x=x_1{x}_2\cdots x_n$ 是长度为r的二进制字符串。任意两个顶点 $\left(i,x\right)$ 和 $\left(j,y\right)$ 相邻，当且仅当 $j=i+1$ 且满足：

(1) $x=y$ 或者；

(2) x和y仅在第j位不同。

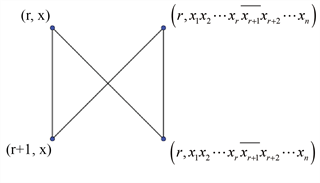
图1给出三维蝴蝶网络 $BF\left(2\right)$。对于蝴蝶网络 $BF\left(n\right)$，将边 $x=y$ 称为竖边，其它的边称为交叉边。记顶点 $\left(i,x\right)$ 为i层的点，显然0层和n层的顶点为2度点，其余顶点均为4度点。因此蝴蝶网络 $BF\left(n\right)$ 的顶点数和边数分别等于 $\left(n+1\right)2^n$ 和 $n{2}^{n+1}$。

引理2.2. 蝴蝶网络 $BF\left(n\right)$ 是哈密尔顿图。

证明：显然，蝴蝶网络 $BF\left(n\right)$ 的诱导子图是 $C_4$，故蝴蝶网络包含一个哈密尔顿圈。因此，蝴蝶网络 $BF\left(n\right)$ 是哈密尔顿图。

引理2.3 [3] 如果H是G的支撑子图，那么 $r\left(H\right)\ge r\left(G\right)$。

引理2.4. [3] 路 $P_n\left(n\ge 3\right)$ 的毁裂度为

图1. (a) BF(2)；(b) BF(n)的诱导子图

$r\left(P_n\right)=\{\begin{array}{ll}-1,\hfill & n为偶数;\hfill \\ 0,\hfill & n为奇数.\hfill \end{array}$

引理2.5. 设X为蝴蝶网络图 $BF\left(n\right)$ 的r-集， $E_i=\left\{\left(i,x\right),\left(i,x_1\overline{x_2}\cdots x_n\right),\cdots ,\left(i,x_1{x}_2\cdots \overline{x_n}\right)\right\}$。蝴蝶网络满足以下性质：

1) 如果 $\left(i,x\right)\subset X$，则有 $\left\{\left(i+1,x\right),\left(i-1,x\right),\left(i-1,x_1{x}_2\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i+1,x_1{x}_2\cdots \overline{x_{i+1}}\cdots x_n\right)\right\}⊈X$。

2) 当 $\left(i,x_1{x}_2\cdots x_n\right)\subset X$ 时，有 $E_i\subset X$。

证明：1) 设图 $G=BF\left(n\right)$，X为图G的r-集。假定 $\left\{\left(i,x\right),\left(i_1,x_1\right),\cdots ,\left(i_{a-1},x_{a-1}\right)\right\}\subseteq X$ 且点集 $\left\{\left(i,x\right),\left(i_1,x_1\right),\cdots ,\left(i_{a-1},x_{a-1}\right)\right\}$ 中的点均有邻点属于X。则分为三种情况讨论并用若干命题证明：

情况1 点集 $\left\{\left(i,x\right),\left(i_1,x_1\right),\cdots ,\left(i_{a-1},x_{a-1}\right)\right\}$ 中的点均不相邻，则设

$\begin{array}{c}{M}_{i,x}=\{\left(i,x\right),\left(i,x_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i,x_1\cdots \overline{x_{i+2}}\cdots x_n\right),\left(i-1,x_1\cdots \overline{x_i}\cdots x_n\right),\left(i+1,x_1\cdots \overline{x_i}\cdots x_n\right),\\ \left(i-1,x_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i+1,x_1\cdots \overline{x_{i+2}}\cdots x_n\right)\}\end{array}$

$X_1=\left\{\left(i-1,x_1\cdots \overline{x_i}\cdots x_n\right),\left(i+1,x_1\cdots \overline{x_i}\cdots x_n\right),\left(i-1,x_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i+1,x_1\cdots \overline{x_{i+2}}\cdots x_n\right)\right\}$，

$X_2\subseteq X_1$。 $X_3=\left(i,x\right)\cup X_2$，根据 $\left|X_3\right|$ 分为5个命题证明：

命题1 当 $\left|X_3\right|=1$ 时， $\omega \left(M_{i,x}-X_3\right)=2$，$\tau \left(M_{i,x}-X_3\right)=3$，$Sc\left(M_{i,x}-X_3\right)=-2$。

命题2 当 $\left|X_3\right|=2$ 时， $\omega \left(M_{i,x}-X_3\right)=2$，$\tau \left(M_{i,x}-X_3\right)=3$，$Sc\left(M_{i,x}-X_3\right)=-3$。

命题3 当 $\left|X_3\right|=3$ 时， $\omega \left(M_{i,x}-X_3\right)=2$，$\tau \left(M_{i,x}-X_3\right)\ge 2$，$Sc\left(M_{i,x}-X_3\right)\le -3$。

命题4 当 $\left|X_3\right|=4$ 时， $\omega \left(M_{i,x}-X_3\right)=2$，$\tau \left(M_{i,x}-X_3\right)=2$，$Sc\left(M_{i,x}-X_3\right)=4$。

命题5 当 $\left|X_3\right|=5$ 时， $\omega \left(M_{i,x}-X_3\right)=2$，$\tau \left(M_{i,x}-X_3\right)=1$，$Sc\left(M_{i,x}-X_3\right)=-4$。

同理，若 $X_3=\left\{\left(i,x\right),\left(i,x_1\cdots \overline{x_{i+1}}\cdots x_n\right)\right\}\cup X_2$ 或 $X_3=\left\{\left(i,x\right),\left(i,x_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i,x_1\cdots \overline{x_{i+2}}\cdots x_n\right)\right\}\cup X_2$。

均有 $Sc\left(M_{i,x}-X_3\right)$ 关于 $\left|X_3\right|$ 单调递减。综上，结论成立。

情况2 点集 $\left\{\left(i,x\right),\left(i_1,x_1\right),\cdots ,\left(i_{a-1},x_{a-1}\right)\right\}$ 中所有点均相邻，设图G的诱导子图为圈 $C_{i,i+1}^x=\left\{\left(i,x\right),\left(i+1,x\right),\left(i,x_1{x}_2\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i+1,x_1{x}_2\cdots \overline{x_{i+1}}\cdots x_n\right)\right\}$，$X^{\prime }=C_{i,i+1}^x\cup C_{i-1,i}^x$，${X^{\prime }}_1=\left\{\left(i-1,x_1\cdots \overline{x_i}\cdots x_n\right),\left(i+1,x_1\cdots \overline{x_i}\cdots x_n\right),\left(i-1,x_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i+1,x_1\cdots \overline{x_{i+2}}\cdots x_n\right)\right\}$，${X^{\prime }}_2\subseteq {X^{\prime }}_1$。根据 $\left|{X^{\prime }}_1\right|$ 通过4个命题证明：

命题1 当 $\left|{X^{\prime }}_1\right|=1$ 时，令 $M_{\left(i,x\right)}=X^{\prime }\cup C_{i+1,i+2}^x$，${X^{\prime }}_3$ 为图 $M_{\left(i,x\right)}$ 的割集。由情况1可得， $Sc\left(M_{i,x}-{X^{\prime }}_3\right)=-2$。

命题2 当 $\left|{X^{\prime }}_1\right|=2$ 时，令 $M_{\left(i,x\right)}=X^{\prime }\cup C_{i+1,i+2}^x\cup C_{i-2,i-1}^x$，${X^{\prime }}_3$ 为图 $M_{\left(i,x\right)}$ 的割集。同理， $Sc\left(M_{i,x}-{X^{\prime }}_3\right)=-2$。

命题3 当 $\left|{X^{\prime }}_1\right|=3$ 时，令 $M_{\left(i,x\right)}=X^{\prime }\cup C_{i+1,i+2}^x\cup C_{i-2,i-1}^x\cup C_{i+1,i+2}^{x_1\cdots \overline{x_{i+2}}\cdots x_n}$，${X^{\prime }}_3$ 为图 $M_{\left(i,x\right)}$ 的割集。同理， $Sc\left(M_{i,x}-{X^{\prime }}_3\right)=-2$。

命题4 当 $\left|{X^{\prime }}_1\right|=4$ 时，令 $M_{\left(i,x\right)}=X^{\prime }\cup C_{i+1,i+2}^x\cup C_{i-2,i-1}^x\cup C_{i+1,i+2}^{x_1\cdots \overline{x_{i+2}}\cdots x_n}\cup C_{i-2,i-1}^{x_1\cdots \overline{x_{i+1}}\cdots x_n}$，${X^{\prime }}_3$ 为图 $M_{\left(i,x\right)}$ 的割集。同理， $Sc\left(M_{i,x}-{X^{\prime }}_3\right)=-2$。

显然， ${\displaystyle \cup M_{\left(i,x\right)}}\subseteq G$。根据上述与引理2.3，结论成立。

情况3 点集 $\left\{\left(i,x\right),\left(i_1,x_1\right),\cdots ,\left(i_{a-1},x_{a-1}\right)\right\}$ 中部分点相邻。此时包含上述两种情况，根据上述可得，若 $\left(i,x\right)\subset X$，则 $\left\{\left(i+1,x\right),\left(i-1,x\right),\left(i-1,x_1{x}_2\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i+1,x_1{x}_2\cdots \overline{x_{i+1}}\cdots x_n\right)\right\}⊈X$。

2) 设 $X_1=E_i$，$X_2=\left\{\left(i,x_1\cdots \overline{x_i}\cdots x_n\right),\left(i,x_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i,x_1\cdots \overline{x_{i+2}}\cdots x_n\right)\right\}$，$\begin{array}{c}{M}_{\left(i,x\right)}=\{\left(i,x_1\cdots \overline{x_i}\cdots x_n\right),\left(i,x_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i,x_1\cdots \overline{x_{i+2}}\cdots x_n\right),\left(i-1,x_1\cdots \overline{x_i}\cdots x_n\right),\\ \left(i+1,x_1\cdots \overline{x_i}\cdots x_n\right),\left(i-1,x_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i+1,x_1\cdots \overline{x_{i+2}}\cdots x_n\right)\}\end{array}$，$G_1={\displaystyle \cup M_{\left(i,x\right)}}$，$X_1\cap G_1={X^{\prime }}_1$，$G-G_1=G_2$。因此，根据性质1与蝴蝶网络图结构，设 $X_3$ 为 $M_i$ 上的割集且 $X_3\subseteq X_2$，考虑 $\left|X_3\right|$ 的大小分为三种情况讨论：

情况1 当 $\left|X_3\right|=2$ 时， $\omega \left(M_{\left(i,x\right)}-X_2\right)\ge \omega \left(M_{\left(i,x\right)}-X_3\right)+1$，$\tau \left(M_{\left(i,x\right)}-X_3\right)\ge \tau \left(M_{\left(i,x\right)}-X_2\right)$。 $Sc\left(M_{\left(i,x\right)}-X_2\right)\ge Sc\left(M_{\left(i,x\right)}-X_3\right)$。

情况2当 $\left|X_3\right|=1$ 时，根据定义，在点集 $X_2$ 中的任意两点属于同一个诱导子图且每个点均属于两个有且仅有一个交点的诱导子图内，故 $\omega \left(M_{\left(i,x\right)}-X_2\right)\ge \omega \left(M_{\left(i,x\right)}-X_3\right)+2$，$\tau \left(M_{\left(i,x\right)}-X_3\right)\ge \tau \left(M_{\left(i,x\right)}-X_2\right)$，$Sc\left(M_{\left(i,x\right)}-X_2\right)\ge Sc\left(M_{\left(i,x\right)}-X_3\right)$。

情况3 当 $\left|X_3\right|=0$ 时，同理可得 $\omega \left(M_{\left(i,x\right)}-X_2\right)\ge \omega \left(M_{\left(i,x\right)}-X_3\right)+3$，$\tau \left(M_{\left(i,x\right)}-X_3\right)\ge \tau \left(M_{\left(i,x\right)}-X_2\right)$，$Sc\left(M_{\left(i,x\right)}-X_2\right)\ge Sc\left(M_{\left(i,x\right)}-X_3\right)$。

设 ${X^{\prime }}_3$ 为 $G_1$ 上的割集。当 $G_1={\displaystyle \cup M_{\left(i,x\right)}}$，综上与引理2.3可知， $\omega \left(G_1-{X^{\prime }}_3\right)-\left|{X^{\prime }}_3\right|\le \omega \left(G_1-{X^{\prime }}_1\right)+\left|{X^{\prime }}_1\right|$，$\tau \left(G_1-{X^{\prime }}_3\right)\ge \tau \left(G_1-{X^{\prime }}_1\right)$，$Sc\left(G_1-{X^{\prime }}_3\right)\le Sc\left(G_1-{X^{\prime }}_1\right)$。因此当 $\left(i,x_1{x}_2\cdots x_n\right)\subset X$ 时，有 $E_i\subset X$。证毕。

引理2.6. 令X为 $G\left(=BF\left(n\right)\right)$ 的r-集，当n为偶数时有 $\omega \left(G-X\right)\le \left(n+2\right)2^{n-1}$。

证明：图G的诱导子图是四阶的圈，记作 $C_4$。显然 $\omega \left(C_4\right)\le 2$。设 $C_4^i=\left\{\left(i,x\right),\left(i+1,x\right),\left(i,x_1{x}_2\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i+1,x_1{x}_2\cdots \overline{x_{i+1}}\cdots x_n\right)\right\}$，${\displaystyle \cup C_4^i}\subseteq G$。根据引理2.3，有 $\omega \left(G-X\right)\le \omega \left({\displaystyle \cup C_4^i}-X\right)$。令 $E_i=\left\{\left(i,x\right),\left(i,x_1\overline{x_2}\cdots x_n\right),\cdots ,\left(i,x_1{x}_2\cdots \overline{x_n}\right)\right\}$，$G_i=E_i\cup E_{i+1}$ 且 $0\le n$，可得 $\omega \left(G_i-E_i\right)=2^n$。由引理2.5可知，此时关于层数i蝴蝶网络 $BF\left(n\right)$ 同构于路 $P_i$。通过引理2.4， $\omega \left(P_i\right)=1+\frac{n}{2}$

且n为偶数。综上所述，当n为偶数时有 $\omega \left(G-X\right)\le \omega \left({\displaystyle \cup C_4^i}-X\right)\le \left(n+2\right)2^{n-1}$。

定理2.7. 令X为 $G\left(=BF\left(n\right)\right)$ 的r-集，那么蝴蝶网络的毁裂度为

$r\left(BF\left(n\right)\right)=\{\begin{array}{ll}{2}^{n-1}-4,\hfill & n为奇数;\hfill \\ 2^n-1,\hfill & n为偶数.\hfill \end{array}$

证明：令X为 $G\left(=BF\left(n\right)\right)$ 的r-集， $E_i=\left\{\left(i,x_1{x}_2\cdots x_n\right),\left(i,x_1\overline{x_2}\cdots x_n\right),\cdots ,\left(i,x_1{x}_2\cdots \overline{x_n}\right)\right\}$，$X^{\ast }=\left\{E_i|i\equiv 1\left(\mathrm{mod}2\right)\right\}$，$X^{\prime }=\left\{E_i|i\equiv 1\left(\mathrm{mod}2\right),i\ge n\right\}$。根据引理3.2，按 $X_i$ 的取点方式分为两种情况讨论，并用若干命题证明：

情况1 若 $X_i=\left\{E_i|i\equiv 0\left(\mathrm{mod}a\right)\right\}$ 且 $1\le a\le n$，则有

命题1 当 $i+1\equiv 0\left(\mathrm{mod}a\right)$ 时， $\omega \left(G-X_i\right)=2^{n+1-a}$，$\left|X_i\right|=\frac{n+1}{a}{2}^n$，$\tau \left(G-X_i\right)=a{2}^{a-1}$。 $Sc\left(G-X_i\right)=2^{n+1-a}-\frac{n+1}{a}{2}^n-a{2}^{a-1}$。

命题2 当 $i+1\cancel{\equiv }0\left(\mathrm{mod}a\right)$ 时， $\omega \left(G-X_i\right)=2^{n+1-a}+1$，$\left|X_i\right|=\lfloor \frac{n+1}{a}\rfloor 2^n$，$\tau \left(G-X_i\right)=a{2}^{a-1}$。 $Sc\left(G-X_i\right)=2^{n+1-a}+1-\lfloor \frac{n+1}{a}\rfloor 2^n-a{2}^{a-1}$。

情况2 令 $G_i=E_i\cup \cdots \cup E_{i+a}$ 且 $X^{\prime }$ 为 $G_i$ 的割集， $X^{\prime }=E_{i+a}$。则有 $\omega \left(G-X^{\prime }\right)=1$，$\left|X^{\prime }\right|=2^n$，$\tau \left(G-X^{\prime }\right)=a{2}^{a-1}$。 $Sc\left(G-X^{\prime }\right)=1-2^n-a{2}^{a-1}$。

综上， $Sc\left(G-X_i\right)$ 与 $Sc\left(G-X^{\prime }\right)$ 均为关于a的单调递减函数。当 $a=1$ 时有最大值。由毁裂度定义可知， $r\left(G\right)\ge Sc\left(G-X^{\ast }\right)$，$r\left(G\right)\ge Sc\left(G-X^{\prime }\right)$ 下面分为两种情况讨论，并利用若干命题完成证明。

情况1 当n为偶数时， $\omega \left(G-X^{\ast }\right)=\left|X^{\ast }\right|=\left(n+2\right)2^{n-1}$，$\tau \left(G-X^{\ast }\right)=1$。根据引理2.2， $\omega \left(G-X\right)\le \omega \left(G-X^{\ast }\right)$，$\tau \left(G-X\right)\ge \tau \left(G-X^{\ast }\right)=1$。分为两个命题证明：

命题1 当 $\left|X\right|\ge \left|X^{\ast }\right|$，$\omega \left(G-X^{\ast }\right)\ge \omega \left(G-X\right)$，$\tau \left(G-X^{\ast }\right)\le \tau \left(G-X\right)$。故 $r\left(G\right)=\omega \left(G-X\right)-\left|X\right|-\tau \left(G-X\right)\le \omega \left(G-X^{\ast }\right)-\left|X^{\ast }\right|-\tau \left(G-X^{\ast }\right)=2^n-1$。因此 $r\left(G\right)=2^n-1$。

命题2 设 $\left|X\right|<\left|X^{\ast }\right|$。当 $a=1$ 时， $Sc\left(G_i-X_i\right)$ 取得最大值。因为 $\left|X\right|<\left|X^{\ast }\right|$ 与引理2.5，此时a最少为2，故 $r\left(G\right)\le Sc\left(G-X^{\ast }\right)$。 $r\left(G\right)=2^n-1$。

情况2 当n为奇数时，

$Sc\left(G-X^{\ast }\right)=\omega \left(G-X^{\ast }\right)-\left|X^{\ast }\right|-\tau \left(G-X^{\ast }\right)\le \omega \left(G-X^{\prime }\right)-\left|X^{\prime }\right|-\tau \left(G-X^{\prime }\right)=Sc\left(G-X^{\prime }\right)=2^{n-1}-4$。

根据引理2.5，在蝴蝶网络 $BF\left(n\right)$ 上关于层数i同构于路 $P_i$。因此，通过蝴蝶网络 $BF\left(n\right)$ 与路 $P_i$ 的结构可知，当n为偶数时有 $\omega \left(G-X^{\ast }\right)-\left|X^{\ast }\right|=2^n$。n为奇数时， $\omega \left(G-X^{\ast }\right)-\left|X^{\ast }\right|=0$ 而 $\omega \left(G-X^{\prime }\right)-\left|X^{\prime }\right|=2^n$。根据命题2， $Sc\left(G_i-X_i\right)$ 是一个关于a的单调递减函数。同理a为2时， $Sc\left(G_i-X_i\right)$ 可以取到最大值。故 $r\left(G\right)=2^{n-1}-4$。证毕。

3. 增广蝴蝶网络的毁裂度

定义3.1. 设 $n\ge 1$ 是一个整数。n维增广蝴蝶网络记为 $ABF\left(n\right)$，其顶点集 $V=\left(i,x\right)$，其中i是非负整数且 $0\le i\le n$，$x=x_1{x}_2\cdots x_n$ 是长度为n的二进制字符串。其中当 $1\le i\le n-1$ 时，顶点 $\left(i,x\right)$ 相邻于顶点

$\left(i+1,x\right)$，$\left(i+1,x_1{x}_2\cdots x_i\overline{x_{i+1}}{x}_{i+2}\cdots x_n\right)$，$\left(i,x_1{x}_2\cdots x_{i-1}\overline{x_i}{x}_{i+1}\cdots x_n\right)$，$\left(i,x_1{x}_2\cdots x_i\overline{x_{i+1}}{x}_{i+2}\cdots x_n\right)$。特别地，当 $i=0$ 时，顶点 $\left(0,x_1{x}_2\cdots x_n\right)$ 相邻于顶点 $\left(1,x_1{x}_2\cdots x_n\right)$，$\left(1,\overline{x_1}{x}_2\cdots x_n\right)$，$\left(0,\overline{x_1}{x}_2\cdots x_n\right)$。当 $i=n$ 时，顶点 $\left(n,x_1{x}_2\cdots x_n\right)$

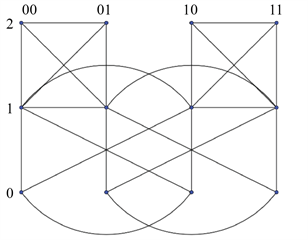
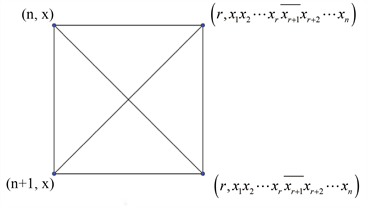
相邻于顶点 $\left(n-1,x_1{x}_2\cdots x_n\right)$，$\left(n,x_1{x}_2\cdots x_{n-1}\overline{x_n}\right)$，$\left(n-1,x_1{x}_2\cdots x_{n-1}\overline{x_n}\right)$。图2给出三维增广蝴蝶网络 $ABF\left(2\right)$ 与其诱导子图。显然增广蝴蝶网络 $ABF\left(n\right)$ 的顶点数和边数分别等于 $\left(n+1\right)2^n$ 和 $3n\times 2^n$。记顶点 $\left(i,x\right)$ 为第i层的点，显然0层和n层的顶点为3度点，其余顶点均为6度点。

引理3.2. 设X为增广蝴蝶网络图 $ABF\left(n\right)$ 的r-集， $E_i=\left\{\left(i,x\right),\left(i,x_1\overline{x_2}\cdots x_n\right),\cdots ,\left(i,x_1{x}_2\cdots \overline{x_n}\right)\right\}$。增广蝴蝶网络满足以下性质：

1) 如果 $\left(i,x\right)\subset X$，则有 $\left\{\left(i+1,x\right),\left(i-1,x\right),\left(i-1,x_1{x}_2\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i+1,x_1{x}_2\cdots \overline{x_{i+1}}\cdots x_n\right)\right\}⊈X$。

2) 当 $\left(i,x_1{x}_2\cdots x_n\right)\subset X$ 时，有 $E_i\subset X$。

图2. (a) ABF(2)；(b) ABF(n)的诱导子图

证明：1) 设 $\begin{array}{c}{M}_i=\{\left(i,x\right),\left(i-1,x\right),\left(i+1,x\right),\left(i,X_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i,X_1\cdots \overline{x_{i+2}}\cdots x_n\right),\\ \left(i-1,X_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i+1,X_1\cdots \overline{x_{i+2}}\cdots x_n\right)\}\end{array}$，X为 $M_i$ 的割集。 $X_i=\left\{\left(i-1,x\right),\left(i+1,x\right),\left(i-1,X_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i+1,X_1\cdots \overline{x_{i+2}}\cdots x_n\right)\right\}$，$X_2\subseteq X_1$ 且 $X_2\ne \varnothing$，分为以下三种情况，并通过若干命题证明。

情况1 令 $X_3=X_2\cup \left\{\left(i,x\right)\right\}$。根据增广蝴蝶网络定义， $\omega \left(G-X_3\right)\equiv 1$，不符合毁裂度定义。

情况2 令 $X_4=X_3\cup \left\{\left(i,X_1\cdots \overline{x_{i+1}}\cdots x_n\right)\right\}$，$X_5=\left\{\left(i,x\right),\left(i,X_1\cdots \overline{x_{i+1}}\cdots x_n\right)\right\}$。有 $\omega \left(M_i-X_4\right)\le \omega \left(M_i-X_5\right)=2$，$\left|X_4\right|>\left|X_5\right|=2$，$\tau \left(M_i-X_5\right)=3$。

命题1 当 $\left|X_4\right|-\left|X_5\right|=1$ 时， $\tau \left(M_i-X_4\right)\le 2$，$Sc\left(M_i-X_4\right)=\omega \left(M_i-X_4\right)-\left|X_4\right|-\tau \left(M_i-X_4\right)\le \omega \left(M_i-X_5\right)-\left|X_5\right|-\tau \left(M_i-X_5\right)=Sc\left(M_i-X_5\right)$。

命题2 当 $\left|X_4\right|-\left|X_5\right|=2$ 时， $\tau \left(M_i-X_4\right)\le 2$，$Sc\left(M_i-X_4\right)\le Sc\left(M_i-X_5\right)$。

命题3 当 $\left|X_4\right|-\left|X_5\right|\ge 2$ 时， $\tau \left(M_i-X_4\right)=1$，$Sc\left(M_i-X_4\right)\le Sc\left(M_i-X_5\right)$。

同理，令 $X_4=X_3\cup \left\{\left(i,X_1\cdots \overline{x_{i+2}}\cdots x_n\right)\right\}$，可得 $Sc\left(M_i-X_4\right)\le Sc\left(M_i-X_5\right)$。

情况3 令 $X_6=X_3\cup \left\{\left(i,X_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i,X_1\cdots \overline{x_{i+2}}\cdots x_n\right)\right\}$，$X_7=\left\{\left(i,x\right),\left(i,X_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i,X_1\cdots \overline{x_{i+2}}\cdots x_n\right)\right\}$。因此， $Sc\left(M_i-X_7\right)=-3=Sc\left(M_i-X_5\right)\ge Sc\left(M_i-X_4\right)$。

$\omega \left(M_i-X_6\right)\le \omega \left(M_i-X_7\right)=2$，$\left|X_6\right|>\left|X_7\right|=3$，$\tau \left(M_i-X_7\right)=2$。同理，分为两种情况讨论：

情况1 当 $\left|X_6\right|-\left|X_7\right|=2$ 时， $\tau \left(M_i-X_6\right)=1$，$Sc\left(M_i-X_6\right)\le Sc\left(M_i-X_7\right)$。

情况2 当 $\left|X_4\right|-\left|X_5\right|>2$ 时， $\tau \left(M_i-X_4\right)=1$，$Sc\left(M_i-X_6\right)\le Sc\left(M_i-X_7\right)$。

综上，当 $\left(i,x\right)\subset X$ 时， $X_1⊈X$。令 $G=ABF\left(n\right)$ 且X为 $ABF\left(n\right)$ 的r-集。显然， $G={\displaystyle \cup M_i}$，根据引理2.3有 $Sc\left(M_i-X_7\right)\le r\left({\displaystyle \cup M_i}-X\right)\le r\left(G-X\right)$。

2) 设 $G=ABF\left(n\right)$，X为G的r-集， $\left(i,x\right)\in X$，$E_i=\left\{\left(i,x\right),\left(i,x_1\overline{x_2}\cdots x_n\right),\cdots ,\left(i,x_1{x}_2\cdots \overline{x_n}\right)\right\}$，考虑任意一排上的点全取与只取其中一部分，根据增广蝴蝶网络结构可知，同一排上任意取点与其邻点所在的诱导子图构成的图同构于 $ABF\left(2\right)$。令 $\begin{array}{c}{M}_i=\{\left(i,x\right),\left(i-1,x\right),\left(i+1,x\right),\left(i,X_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i,X_1\cdots \overline{x_{i+2}}\cdots x_n\right),\\ \left(i-1,X_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i+1,X_1\cdots \overline{x_{i+2}}\cdots x_n\right)\}\end{array}$，$X_1=\left\{\left(i,x\right),\left(i,X_1\cdots \overline{x_{i+1}}\cdots x_n\right),\left(i,X_1\cdots \overline{x_{i+2}}\cdots x_n\right),\left(i,X_1\cdots \overline{x_{i+3}}\cdots x_n\right)\right\}$，$X_2\subseteq X_1$ 且 $X_2\ne \varnothing$。 $Sc\left(M_i-X_1\right)=\omega \left(M_i-X_1\right)-\left|X_1\right|-\tau \left(M_i-X_1\right)=4-4-2=-2$。根据性质1，分为三种情况讨论：

情况1 当 $\left|X_2\right|=3$ 时， $\omega \left(M_i-X_2\right)=3$，$\tau \left(M_i-X_2\right)=5$。 $Sc\left(M_i-X_2\right)=3-3-5\le Sc\left(M_i-X_1\right)$。

情况2 当 $\left|X_2\right|=2$ 时， $\omega \left(M_i-X_2\right)=2$，$5\le \tau \left(M_i-X_2\right)\le 8$。 $Sc\left(M_i-X_2\right)\le Sc\left(M_i-X_1\right)$。

情况3 当 $\left|X_2\right|\le 1$ 时， $\omega \left(M_i-X_2\right)=1$，$\tau \left(M_i-X_2\right)=12$。 $Sc\left(M_i-X_2\right)\le Sc\left(M_i-X_1\right)$。

显然， $G={\displaystyle \cup M_i}$。设 $G_1=E_i\cup E_{i-1}\cup E_{i+1}$，$G-G_1=G_2$，$X_3=\left(G_2\cap X\right)\cup E_i$，$\left|X\right|-\left|X_3\right|=a$。在图G中，每两个点最多只在一个诱导子图 $K_4$ 内，且均为两个诱导子图 $K_4$ 的相交点。根据性质1 与引理2.3可得， $\omega \left(G-X\right)\le \omega \left(G-X_3\right)-a$，$\tau \left(G-X\right)\ge \tau \left(G-X_3\right)$。 $r\left(G-X\right)=\omega \left(G-X\right)-\left|X\right|-\tau \left(G-X\right)\le \omega \left(G-X_3\right)-\left|X_3\right|-\tau \left(G-X_3\right)=Sc\left(G-X_3\right)$。证毕。

定理3.3. 令X为 $G\left(=ABF\left(n\right)\right)$ 的r-集，那么增广蝴蝶网络的毁裂度为