云南民族大学数学与计算机科学学院，云南 昆明

收稿日期：2023年6月17日；录用日期：2023年7月21日；发布日期：2023年7月28日

摘要

称一个图为对称图，如果它的自同构群在这个图的弧集上是传递的。文中给出了40p阶三度对称图的分类的一些结论，其中p为素数。

关键词

对称图，自同构群，Cayley图

Cubic Symmetric Graphs of Order 40p

Luqing Zhao^*, Xin Ru

School of Mathematics and Computer Sciences, Yunnan Minzu University, Kunming Yunnan

Received: Jun. 17^th, 2023; accepted: Jul. 21^st, 2023; published: Jul. 28^th, 2023

ABSTRACT

A graph is said to be symmetric if its automorphism group acts transitively on its arcs. Some conclusions of classification of cubic symmetric graphs of order 40p are given in this paper, where p is prime.

Keywords:Symmetric Graph, Automorphism Group, Cayley Graph

Copyright © 2023 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

本文所考虑的图都是有限、连通、简单无向图。

对于图 $\Gamma$ ，分别用 $V\left(\Gamma \right)$ ， $E\left(\Gamma \right)$ 和 $A\left(\Gamma \right)$ 表示图 $\Gamma$ 的顶点集，边集和自同构群。设s是一个正整数，称 $\Gamma$ 中 $s+1$ 个顶点序列 $V_0{V}_1\cdots V_S$ 为一个s-弧，如果 $\left(V_i,V_{i+1}\right)\in E\left(\Gamma \right)$ ， $0\le i\le s-1$ ，并且对 $s\ge 2$ ，有 $V_i\ne V_{i+2}$ ， $0\le i\le s-2$ 。称 $\Gamma$ 为s-弧传递图，如果 $\text{Aut}\left(\Gamma \right)$ 在 $\Gamma$ 的所有s-弧上是传递的。称 $\Gamma$ 为s-传递图，如果 $\Gamma$ 是s-弧传递的，但不是 $\left(s+1\right)$ -弧传递的。

研究群与图里面的对称性，也就是图的自同构群作用在图的顶点集，边集，弧集等上面的传递性，对称图的研究是一个热门的话题，我们研究对称图一般从小度数开始研究。而对于三度图的研究，很多作者都有了一些显著的成果。Chao，Cheng分别在文献 [1] [2] 里完全分类了阶为p和2p的对称图。Conder在文献 [3] 中分类了所有阶小于或等于768个顶点的三度对称图。Tutte在文献 [4] 里给出了三度对称图的点稳定子后，对于三度对称图的分类才得到进一步的研究。Feng在文献 [5] [6] 中分类了8p，10p，8p²，10p²阶的三度对称图。Oh在文献 [7] [8] 里完全分类了14p，16p阶的三度对称图。Cheng在文献 [9] 分类了阶为 $2p^n$ 的三度对称图。Ling在文献 [10] 中完全分类了四倍的奇无平方整数阶的三度对称图。根据这些研究得到的背景以及结果，可以为我们分类以下的图提供方法。

现在，三度对称图的分类情况已经研究得差不多了，但是40p阶的三度对称图还没有被分类。目前，这篇文章只考虑图自同构群A可解的情况，所以分类不完整，在今后的研究中会继续考虑这个问题，尝试用新的方法来将40p阶的三度对称图完全分类。下面的定理是分类得到的结论。

定理1.1 设 $\Gamma$ 是一个40p阶的三度对称图。令 $\text{A}=\text{Aut}\left(\Gamma \right)$ ，F为A的Fitting子群，假设A是可解的，则下列之一成立。

1) F在 $V\left(\Gamma \right)$ 上传递，则。

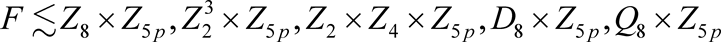2) F在 $V\left(\Gamma \right)$ 上恰好有两个轨道，F是一个二部图。

3) F在 $V\left(\Gamma \right)$ 上至少有三个轨道， $\Gamma$ 是 ${\Gamma }_F$ 的正规覆盖， ${\Gamma }_F$ 是三度的 $\text{<mover accent="true"> A <mo> ¯ </mo> </mover>}=\text{A}/F$ -弧传递图且 $\text{<mover accent="true"> A <mo> ¯ </mo> </mover>}$ 是对称的。

2. 预备知识

在这一节中我们将引用一些基本的结果，方便后面的讨论。设G是有限群，G的所有幂零正规子群的乘积 $F\left(G\right)$ 仍为G的幂零正规子群，叫做G的Fitting子群，下面的引理(参见文献 [11] ，p. 30，推论)。

定理2.1 设 $F\left(G\right)$ 是G的Fitting子群， $C_G\left(F\right)/F$ 不包含 $\ne 1$ 的可解正规子群，若G可解，则 $C_G\left(F\right)\le F$ 。

对于轨道长公式，有下面的定理，参见文献 [12] 。

定理2.2 设有限群G作用在有限集合 $\Omega$ 上， $\alpha \in \Omega$ ，则 $\left|{\alpha }^G\right|=\left|G:G_{\alpha }\right|$ ，特别地，轨道 ${\alpha }^G$ 的长是 $\left|G\right|$ 的因子。

设G是有限群，H是G的子群， $C_G\left(H\right)$ 是H在G中的中心化子， $N_G\left(H\right)$ 是H在G中的正规。由文( [12] ，第I章，定理5.7)得下面“N/C”定理。

定理2.3 设 $H\le G$ ，则 $N_G\left(H\right)/C_G\left(H\right)$ 同构于 $\text{Aut}\left(H\right)$ 的一个子群。

称Cayley图 $\Gamma =\text{Cayley}\left(G,S\right)$ 是正规的，如果G的右正则表示 $R\left(G\right)$ 是 $\text{Aut}\left(\Gamma \right)$ 的正规子群，令： $\text{Aut}\left(G,S\right)=\left\{\alpha \in \text{Aut}\left(G\right)|S^{\alpha }=S\right\}$ ，令 $\text{A}=\text{Aut}\left(\Gamma \right)$ 。设 $N_{\text{A}}\left(R\left(G\right)\right)$ 为 $R\left(G\right)$ 在A中的正规化子，进一步由文献( [13] ，引理2.1)有下面的引理。

引理2.4 $N_{\text{A}}\left(R\left(G\right)\right)=R\left(G\right)\text{Aut}\left(G,S\right)$ 。

因此 $\Gamma$ 正规的当且仅当 $\text{Aut}\left(\Gamma \right)=R\left(G\right)\text{Aut}\left(G,S\right)$ 。

以下引理是关于三度对称图的点稳定子的结构，由( [14] ，命题2~5)确定。

引理2.5 设 $\Gamma$ 是一个连通的五度 $\left(G,s\right)$ -传递图，其中 $G\le \text{Aut}\left(\Gamma \right)$ ， $s\ge 1$ ，设 $\alpha \in V\left(\Gamma \right)$ ，则下列表述之一成立：

1) 如果 $G_{\alpha }$ 是可解的，则 $\left|G_{\alpha }\right||80$ 且 $s\le 3$ 。此外， $\left(G_{\alpha },s\right)$ 见表1。

表1. 可解的点稳定子

2) 如果 $G_{\alpha }$ 是不可解的，则 $\left|G_{\alpha }\right||2^9\cdot 3^2\cdot 5$ 且 $2\le s\le 5$ 。此外， $\left(G_{\alpha },s\right)$ 见表2。

表2. 非可解的点稳定子

由( [5] ，定理5.1)可以得到8p阶三度对称图的分类。

引理2.6 令p为素数， $\Gamma$ 是阶为8p的三度对称图，则下列之一成立。

1) $\Gamma$ 是1-正则的，当 $3|p-1$ 时， $\Gamma \cong C{Q}_p$ 和 $\text{Aut}\left(\Gamma \right)\cong Z_p⋊\left(Z_2^3⋊Z_3\right)$ 。

2) $\Gamma$ 是2-正则的，当 $p=2,3$ 或7时， $\Gamma$ 同构于 $C{Q}_2,C{Q}_3$ 或Lorimer图。

3) $\Gamma$ 是3-正则的，当 $p=7$ 或5时， $\Gamma$ 同构于典范双重覆盖图 $D_{20}^{\left(2\right)}$ 或 $D_{28}^{\left(2\right)}$ 。

对于图 $\Gamma$ 以及点传递子群 $G\le \text{Aut}\left(\Gamma \right)$ ，令N是 $\Gamma$ 在 $V\left(\Gamma \right)$ 上是不传递的正规子群。用 $V\left({\Gamma }_N\right)$ 表示 $V\left(\Gamma \right)$ 中的N的轨道的集合，由N诱导的正规商图 ${\Gamma }_N$ 定义为顶点集 $V\left({\Gamma }_N\right)$ 的图。在商图 ${\Gamma }_N$ 中 $\left(B_1,B_2\right)\in E\left({\Gamma }_N\right)$ 当且仅当 $x\in B_1$ 和 $y\in B_2$ ，使得 $\left(x,y\right)\in E\left(\Gamma \right)$ 。文献( [15] ，引理2.5)和( [16] ，定理4.1)为研究三度对称图提供了一种基本的方法。

定理2.7 设 $\Gamma$ 是奇数度的G-弧传递图，令 $N⊲G$ 在 $V\left(\Gamma \right)$ 上至少有三个轨道，那么下列的陈述成立。

(i) N是 $V\left(\Gamma \right)$ 上的半正则， $G/N\le \text{Aut}\left({\Gamma }_N\right)$ ， $\Gamma$ 是 ${\Gamma }_N$ 的正规覆盖。

(ii) $G_{\alpha }\cong {\left(G/N\right)}_{\delta }$ ，其中 $\alpha \in V\left(\Gamma \right)$ ， $\delta \in V\left({\Gamma }_N\right)$ 。

(iii) $\Gamma$ 是 $\left(G,s\right)$ -传递的当且仅当 ${\Gamma }_N$ 是 $\left(G/N,s\right)$ -传递。

3. 定理1.1的证明

设 $\Gamma$ 是一个阶为40p的三度对称图，根据引理2.5， $\left|{\text{A}}_{\alpha }\right||2^4\cdot 3$ ，所以 $\left|\text{A}\right||2^7\cdot 3\cdot 5p$ 。接下来，我们考虑A是可解的情况。

证明：设F是A的Fitting子群，根据定理2.1， $F\ne 1$ ，且 $C_{\text{A}}\left(F\right)\le F$ ，因为 $\left|V\left(\Gamma \right)\right|=40p$ ，A没有非平凡的正规s-子群，其中 $s\ne 2,5$ ，p是一个素数，我们有： $F=O_2\left(\text{A}\right)\times O_5\left(\text{A}\right)\times O_p\left(\text{A}\right)$ 。

其中 $O_2\left(\text{A}\right),O_5\left(\text{A}\right),O_p\left(\text{A}\right)$ 分别表示A的最大正规2-，5-，p-子群。

对于任意的 $q\in \left\{2,5,p\right\}$ ，因为A在 $V\left(\Gamma \right)$ 上的作用是传递的， $O_q\left(\text{A}\right)⊲\text{A}$ ，则 $O_q\left(\text{A}\right)$ 在顶点集 $V\left(\Gamma \right)$ 上所有轨道的长都相等。根据定理2.2的轨道公式 $\alpha \in V\left(\Gamma \right)$ ， ${\alpha }^{O_q\left(\text{A}\right)}=\left|O_q\left(\text{A}\right):{\left(O_q\left(\text{A}\right)\right)}_{\alpha }\right|=t$ ，再设 $O_q\left(\text{A}\right)$ 在 $V\left(\Gamma \right)$ 上有m个轨道，因为 $p\ge 3$ 且 $p\ne 5$ 时， $40p=mt\Rightarrow m=40p/t=30$ ，所以 $O_q\left(\text{A}\right)$ 在 $V\left(\Gamma \right)$ 上至少有30个轨道。又根据定理2.7(i)可得 $O_q\left(\text{A}\right)$ 在 $V\left(\Gamma \right)$ 上是半正则的，此外 $\left|O_2\left(\text{A}\right)\right|\le 8$ ， $O_5\left(\text{A}\right)\le Z_5$ ， $O_p\left(\text{A}\right)\le Z_p$ ，下面对F进行分情况讨论：

根据 $\left|O_2\left(\text{A}\right)\right|\le 8$ ，则8阶群有：循环群 $Z_8$ ，交换群 $Z_2\times Z_2\times Z_2$ ，交换群 $Z_4\times Z_2$ ，非交换群 $D_8=\langle a,b|a^4=b_2=1,ba=a^{-1}b\rangle$ ，非交换群 $Q_8=\langle a,b|a^4=1,b_2=a^2,ba=a^{-1}b\rangle$ 。

如果F在 $V\left(\Gamma \right)$ 上是传递的，当F是交换群时： $F=Z_8\times Z_5\times Z_p$ ， $F=Z_2\times Z_2\times Z_2\times Z_5\times Z_p$ ， $F=Z_4\times Z_2\times Z_5\times Z_p$ 。如果F在 $V\left(\Gamma \right)$ 上是传递的，那么 $\left|F\right|=40p$ 在 $V\left(\Gamma \right)$ 是正则的， $\Gamma$ 是F的Cayley图。设 $\Gamma =\text{Cayley}\left(F,S\right)$ ，其中 $S=S^{-1}\subseteq F\backslash \left\{1\right\}$ ， $\left|S\right|=3$ ，因为 $F⊲\text{A}$ ，则 $\Gamma$ 是正规Cayley图，根据引理2.4可得 $\text{A}=F:\text{Aut}\left(F,S\right)$ ，又因为 $\Gamma$ 是弧传递的，由弧传递的等价条件得知 ${\text{A}}_1=\text{Aut}\left(F,S\right)\le \text{Aut}\left(F\right)$ 在 $\Gamma \left(1\right)=S$ 上是传递的，其中1表示 $\Gamma$ 的顶点对应F的单位元，S里的元素都是群F里的元素，对于 $\forall S_1,S_2\in F$ ， $\exists \sigma \in \text{Aut}\left(F\right)$ ，使得 $S_1^{\sigma }=S_2$ ，则 $\left|S_1\right|=\left|S_2\right|$ ，所以S中的元素具有相同的阶，并令其阶为t。当 $t=1$ 时， $\left|S\right|=3$ ，有三个单位元，显然是矛盾的，当 $t\ge 2$ 时，不能得到矛盾。当F是非交换群时，用所学的知识不能得到矛盾。但是我们有。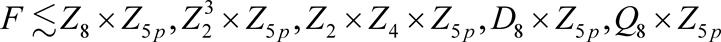

如果F在 $V\left(\Gamma \right)$ 上是至少有三个轨道，则定理2.7(i)表明 ${\Gamma }_F$ 是A/F弧传递的，根据假设 $F=Z_8\times Z_5\times Z_p$ 时，因为F在 $V\left(\Gamma \right)$ 上是半正则的且F为交换群，所以 $F\le C_{\text{A}}\left(F\right)$ ，又根据引理2.1 $C_{\text{A}}\left(F\right)\le F$ ，即 $F=C_{\text{A}}\left(F\right)$ 。根据定理2.3， $F\le \text{A}$ ，则 $N_A\left(F\right)/C_A\left(F\right)$ 同构于 $N_A\left(F\right)/C_A\left(F\right)$ 的一个子群，又因为 $F⊲\text{A}$ ，所以 $N_{\text{A}}\left(F\right)=\text{A}$ 。即 $\text{A}/F=\text{A}/C_{\text{A}}\left(F\right)$ 同构于 $\text{Aut}\left(F\right)$ 的一个子群。由于循环群的自同构群是交换群，可得 $\text{Aut}\left(F\right)$ 是交换群，因此A/F是可交换的。由弧传递的等价条件可得对于 $\forall v\in V\left({\Gamma }_F\right)$ ， ${\left(\text{A}/F\right)}_v$ 在它的邻域上传递。因为A/F作用在 $V\left({\Gamma }_F\right)$ 上是传递的且是交换群，则A/F是正则的，所以 ${\left(\text{A}/F\right)}_v=1$ ，出现矛盾。

当F为其它群时，F在 $V\left(\Gamma \right)$ 上是至少有三个轨道。在正规块图里面，原图度数与块图的度数相等，则 $\Gamma$ 是 ${\Gamma }_F$ 的正规覆盖， ${\Gamma }_F$ 是三度的 $\text{<mover accent="true"> A <mo> ¯ </mo> </mover>}=\text{A}/F$ -弧传递图。设A存在非平凡的正规子群F且 $\text{<mover accent="true"> A <mo> ¯ </mo> </mover>}=\text{A}/F$ ，设 $\left(B_1,B_2\right)$ ， $\left(B_3,B_4\right)$ 是块图 ${\Gamma }_F$ 的两条弧，由块图的定义知道， $v_1\in B_1,v_2\in B_2,v_3\in B_3,v_4\in B_4$ 。使得 $\left(v_1,v_2\right)$ 和 $\left(v_3,v_4\right)$ 是图 $\Gamma$ 的两条弧，于是 $\exists g\in G$ ，我们有 $v_1^g=v_3$ ， $v_2^g=v_4$ ，令 $B_1=B^{g_1}$ ， $B_2=B^{g_2}$ ， $B_3=B^{g_3}$ ， $B_4=B^{g_4}$ 。 $v_1^g=v_3\in B_1^g\cap B_3=B^{g_{1}g}\cap B^{g_3}$ ， ${\left(v_3\right)}^{{\left(g_3\right)}^{-1}}\in B^{g_{1}g{\left(g_3\right)}^{-1}}\cap B\Rightarrow$ $\ne \varnothing$， $B^{g_{1}g{\left(g_3\right)}^{-1}}=B\Rightarrow B_1^g=B_3$ 。同理， $B_2^g=B_4$ ，于是 ${\Gamma }_F$ 的 $\text{<mover accent="true"> A <mo> ¯ </mo> </mover>}=\text{A}/N$ 对称的。

如果F恰好在 $V\left(\Gamma \right)$ 上有两个轨道，根据原图中的轨道个数为块图中的顶点个数，可得块图顶点的个数为2。对于任意的 $B\in \mathcal{B}$ ，设 $u,v\in B$ 且 $\left\{u,v\right\}\in E\left(\Gamma \right)$ ，又设 $v^{\prime }\in {\Gamma }_1\left(u\right)$ ， ${\Gamma }_1\left(u\right)$ 为u在图 $\Gamma$ 中的领域。 $\left\{u,v^{\prime }\right\}\in E\left(\Gamma \right)$ ，由 $\Gamma$ 得的G-对称性， $\exists g\in G$ ，使得 $u^g=u$ ， $v^g=v$ $\Rightarrow$$g\in G_u$，而 $u\in B$ ，有 $u^g\in B^g$ $\Rightarrow$$u\in B^g\cap B$，又因为B为块， $B^g=B$ ， $v\in B$ $\Rightarrow$$v^g\in B^g=B$$\Rightarrow$$v^{\prime }\in B$。从而 ${\Gamma }_1\left(u\right)\subseteq B$ ，继续这样的推理， $\Gamma$ 的包含u的连通分支也含于B中。因为 $\Gamma$ 是连通的，只有一条连通分支，且含于B中， $B=V\left(\Gamma \right)$ ，所以产生矛盾。则B中不含图 $\Gamma$ 的边，这两个轨道就构成了二部图的二部划分，于是 $\Gamma$ 是二部图。

文章引用

赵路清,茹 昕. 40p三度对称图
Cubic Symmetric Graphs of Order 40p[J]. 理论数学, 2023, 13(07): 2098-2102. https://doi.org/10.12677/PM.2023.137216

参考文献