Pure Mathematics
Vol.
14
No.
01
(
2024
), Article ID:
79924
,
15
pages
10.12677/PM.2024.141022
惯性对称交替方向乘子算法
田明珠1,文 萌1,李 军2
1西安工程大学,理学院,陕西 西安
2琼台师范学院,体育学院,海南 海口
收稿日期:2023年12月13日;录用日期:2023年12月18日;发布日期:2024年1月26日

摘要
在本文中提出一种惯性对称交替方向乘子法求解两分块凸极小化优化问题,文章中证明了所提算法收敛到原问题的最优解,最后通过数据分析,验证所提算法的有效性和优越性。
关键词
交替方向乘子法,收敛性,线性约束凸优化问题,惯性对称交替方向乘子法

Inertial Symmetric Alternating Direction Multiplier Algorithm
Mingzhu Tian1, Meng Wen1, Jun Li2
1School of Science, Xi’an Polytechnic University, Xi’an Shaanxi
2College of Physical Education, Qiongtai Normal University, Haikou Hainan
Received: Dec. 13th, 2023; accepted: Dec. 18th, 2023; published: Jan. 26th, 2024

ABSTRACT
In this paper, an inertial symmetric alternating direction multiplier method is proposed to solve the two-partite convex miniaturization optimization problem, in which it is proved that the proposed algorithm converges to the optimal solution of the original problem, and finally, the effectiveness and superiority of the proposed algorithm is verified through the data analysis.
Keywords:Alternating Direction Multiplier Method, Convergence, Linearly Constrained Convex Optimization Problems, Inertially Symmetric Alternating Direction Multiplier Method

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在本文中主要考虑以下复合优化问题:
(1)
其中
和
是正则下半连续凸函数,
和
是非零有界线性算子,
是实Hilbert空间,
。
交替方向乘子法(ADMM)是求解问题(1)的一种常用算法,ADMM最早是由Gabay [1] 、Glowinski [2] 提出,ADMM算法的迭代步骤为
(2)
Lorenz [3] 提出了向前向后分裂算法,随后在文献 [4] [5] [6] 的基础上结合Nesterov加速方法对算法进行改进,求解两分块问题的方法还有惯性Douglas-Rachford算子分裂算法 [7] 、惯性ADMM [8] 、惯性三算子分裂算法 [9] 等算法。Chen [10] 等人通过结合邻近ADMM [11] 算法提出求解带有线性约束可分离凸优化问题的惯性邻近ADMM算法,并证明了算法的收敛性,薛中会等人 [12] 对可分离凸优化问题采用惯性技术,同时引入随机加速的随即变量更新步长,提出了惯性近似松弛交替方向乘子法。
Tseng [13] 中提出了交替极小化算法(AMA),迭代步骤如下
(3)
为了加速(3),Goldstein在FISTA的基础上求解(1)的对偶问题,得到加速AMA,迭代步骤如下
(4)
其中Chambolle [14] 证明了迭代序列
的收敛性。吴双双在 [15] 中提出了一种惯性的交替极小化算法用来解决问题(1)算法迭代步骤如下
(5)
其中
。
问题(1)的特例有许多,例如财务和统计问题 [16] ,资源分配问题 [17] ,闭凸集交集上的投影问题 [18] [19] ,具有约束的全变分图像去噪问题 [20] [21] [22] 等。下面介绍一下具有约束的全变分图像去噪问题:
(6)
(6)式是有约束的,通过加入示性函数
,由于
,(6)可以表示为
(7)
设
,
,因此(7)可以表示为
(8)
上述问题没有引入对称步,因此本文考虑,在吴 [5] 的基础上,引入一步对称步骤求解问题(1),本文证明所提算法的收敛到问题(1)的最优解,通过数据分析,与已有的ADMM算法比较,验证新算法的有效性和优越性。
下面给出文章中会用到的一些符号,如表1所示。
表1. 符号对照表
2. 预备知识
定义1. 给定一个正常凸函数
,它在点x处的次微分定义为:
其中
里的元素称为函数f在点x处的次梯度,如果
,称函数f在点x处是可微的。
定义2. 设凸函数
,定义f在点
的Fenchel共轭函数:
,
可知共轭函数
是闭凸函数。
定义3. 对任意
,令
是闭凸函数,若满足
则称
为f在点
处的次梯度,f在x处次梯度的全体称为f在x处的次微分,记为
。
3. 惯性对称ADMM算法收敛性分析
在本节中,给出具体求解问题(1)的新算法,具体格式如下:
定理1 假设拉格朗日函数的鞍点是非空的,且
,
,
是由算法1生成的序列,如果
满足下列条件,存在
,使得
,
,
是非递减序列且满足
则存在拉格朗日函数的一组鞍点
,使得
①
②
③
④
证明
问题(1)的拉格朗日函数为
(9)
其中
是拉格朗日乘子。
问题(1)的增广拉格朗日函数为
(10)
问题(1)的对偶问题为
(11)
其中
分别是f和g的Fenchel共轭。
应用惯性邻近梯度算法求解(4)
(12)
其中,
设
,则有
等价于
(13)
将
代入(12)且有邻近算子定义可得
(14)
又
,所以(14)可以化为
(15)
上述一阶优化条件可得
(16)
设
,可以得到
(17)
对(17)进行变形可以得到
(18)
由算法第6步可以得到(17)等价于
(19)
因此
(20)
这是新算法的第5步。
新算法的第3步和第5步由一阶优化条件可以得到
(21)
(22)
由f和g单调有
(23)
(24)
现在将(12)和(13)两式相加可以得到
(25)
整理可得
(26)
由算法第4步、算法第6步和
可以得到
(27)
将(26)代入(25)可以得到
(28)
根据余弦等式,可以将(27)化简为
(29)
现在分开算(28)左边第一项等于
(30)
左边第二项等于
(31)
左边第三项等于
(32)
将(29) (30) (31)相加并代入(28)可以得到
(33)
继续化简(32)
(34)
(35)
(36)
因此可以得到
(37)
根据算法第二步可以得到
(38)
(39)
将(38)代入(37)
(40)
因此(36)等价于
(41)
(42)
由
以及算法的第1步可以得到
(43)
所以(41)可以化为
(44)
由算法的第4步和第6步可得
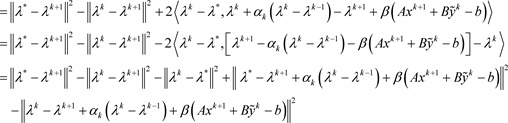
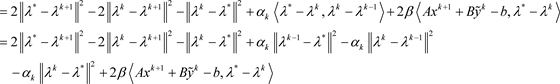 (45)
(45)
代入(1.33)可得
(46)
由于
所以(45)可以化为
(47)
设
,所以(46)可以化为
(48)
对(45)进行整理可得
(49)
对(48)两边同时求和
(50)
上式两边同时取极限可以得到
(51)
因此
①②得证。
由于
由(12)式可得
(52)
又
,所以(51)可以化为
(53)
由算法1第3步、第5步的一阶优化条件可得
(54)
即
(55)
根据次微分定义可以得到
(56)
现在将(55)中两式相加可得
(57)
又因为
,
,所以(56)可以化为
(58)
结合(52)和(57)可以得到
(59)
综上,定理1得证。
4. 数据分析
在本节中,我们将给出所提算法的数值分析,具体来说,我们比较了ADMM算法和惯性对称ADMM算法,我们采用以下目标函数和约束条件:
(60)
上式(60)的拉格朗日表达式为
(61)
在迭代次数为30的情况下,ADMM和惯性对称ADMM算法如下图1所示。
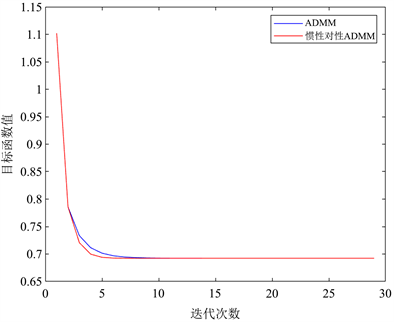
Figure 1. Plot of results comparing ADMM and inertial ADMM
图1. ADMM和惯性ADMM比较结果图
注:由图可知本文新算法较ADMM在相同迭代次数下其目标函数值收敛速度相对较快。
5. 结论
提出求解目标函数的惯性对称ADMM算法,并进行了收敛性分析,最后,数值实验表明,新算法与ADMM算法相比较优越。
文章引用
田明珠,文 萌,李 军. 惯性对称交替方向乘子算法
Inertial Symmetric Alternating Direction Multiplier Algorithm[J]. 理论数学, 2024, 14(01): 203-217. https://doi.org/10.12677/PM.2024.141022
参考文献
- 1. Gabay, D. (1983) Chapter IX Applications of the Method of Multipliers to Variational Inequalities. Studies in Mathe-matics and Its Applications, 15, 299-231. https://doi.org/10.1016/S0168-2024(08)70034-1
- 2. Glowinski, R. and Marroco, A. (1975) Sur l’approximation, par elements finis d’ordre un, et laresolution, par penalisation-dualite, d’une classe de problemes de dirichlet non lineares. Revue Francaise d’Automatique, Informatique et Recherche Operationelle, 9, 41-76. https://doi.org/10.1051/m2an/197509R200411
- 3. Lorenz, D.A. and Pock, T. (2015) An Inertial Forward-Backward Algorithm for Monotone Inclusions. Journal of Mathematical Imaging and Vision, 51, 311-325. https://doi.org/10.1007/s10851-014-0523-2
- 4. Moudafi, A. and Oliny, M. (2003) Convergence of a Splitting Inertial Proximal Method for Monotone Operators. Journal of Computational and Applied Mathematics, 155, 447-454. https://doi.org/10.1016/S0377-0427(02)00906-8
- 5. Alvarez, F. and Attouch, H. (2001) An Inertial Proximal Method for Maximal Monotone Operators via Discretization of a Nonlinear Oscillator with Damping. Set-Valued Analysis, 9, 3-11. https://doi.org/10.1023/A:1011253113155
- 6. Attouch, H. and Cabot, A. (2020) Convergence of a Relaxed Inertial Proximal Algorithm for Maximally Monotone Operators. Mathematical Programming, 184, 243-287. https://doi.org/10.1007/s10107-019-01412-0
- 7. Bot, R.I., Csetnek, E.R. and Hendrich, C. (2015) Inertial Douglas-Rachford Splitting for Monotone Inclusion Problems. Applied Mathematics and Computation, 256, 472-487. https://doi.org/10.1016/j.amc.2015.01.017
- 8. Cui, F.Y., Tang, Y.C. and Yang, Y. (2019) An Inertial Three-Operator Splitting Algorithm with Applications to Image in Painting. Application of Set-Valued Analysis and Optimization, 1, 113-134.
https://doi.org/10.23952/asvao.1.2019.2.03
- 9. Jia, H., Liu, S. and Dang, Y. (2021) An Inertial Accelerated Al-gorithm for Solving Split Feasibility Problem with Multiple Output Sets. Journal of Mathematics, 2021, 1-12. https://doi.org/10.1155/2021/6252984
- 10. Chen, C.H., Chan, R.H., Ma, S.Q., et al. (2015) Inertial Proximal ADMM for Linearly Constrained Separable Convex Optimization. SIAM Journal on Imaging Sciences, 8, 2239-2267. https://doi.org/10.1137/15100463X
- 11. Attouch, H. and Soueycatt, M. (2008) Augmented Lagrangian and Proximal Alternating Direction Methods of Multipliers in Hilbert Spaces. Applications to Games, PDE’s and Control. Pacific Journal of Optimization, 5, 17-37.
- 12. 薛中会, 殷倩雯, 党亚峥. 求解可分离凸优化问题的惯性近似松弛交替方向乘子法[J]. 上海理工大学学报, 2022, 44(2): 204-212.
- 13. Tseng, P. (1991) Applications of a Splitting Algorithm to Decomposition in Convex Programming and Variational Inequalities. SIAM Journal on Control and Op-timization, 29, 119-138. https://doi.org/10.1137/0329006
- 14. Chambolle, A. and Dossal, Ch. (2015) On the Con-vergence of the Iterates of the “Fast Iterative Shrinkage/Thresholding Algorithm”. Journal of Optimization Theory and Applications, 166, 968-982.
https://doi.org/10.1007/s10957-015-0746-4
- 15. 吴双双, 唐玉超. 一种惯性交替极小化算法及其应用[J]. 南昌大学学报(理科版), 2022, 46(5): 481-491.
- 16. Tao, M., Yuan, X.M. and He, B.S. (2011) Solving a Class of Matrix Minimization Problems by Linear Variational Inequality Approaches. Linear Algebra and Its Applications, 434, 2343-2352. https://doi.org/10.1016/j.laa.2010.11.041
- 17. Beck, A. and Teboulle, M. (2014) A Fast Dual Proxi-mal Gradient Algorithm for Convex Minimization and Applications. Operations Research Letters, 42, 1-6. https://doi.org/10.1016/j.orl.2013.10.007
- 18. Boyd, S., Parikh, N., Chu, E., Peleato, B. and Eckstein, J. (2010) Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Foundations and Trends in Machine Learning, 3, 1-122.
https://doi.org/10.1561/9781601984616
- 19. 宗春香, 蔡用, 唐玉超. 有限族非空闭凸集交上的投影算子迭代算法[J]. 南昌大学学报, 2018, 42(4): 327-338.
- 20. Beck, A. and Teboulle, M. (2009) Fast Gradient-Based Algo-rithms for Constrained Total Variation Image Denoising and Deblurring Problems. IEEE Transactions on Image Pro-cessing, 18, 2419-2434.
https://doi.org/10.1109/TIP.2009.2028250
- 21. Ng, M.K., Weiss, P. and Yuan, X.M. (2010) Solving Constrained Total-Variation Image Restoration and Reconstruction Problems via Alternating Direction Methods. SIAM Journal on Scientific Computing, 32, 2710-2736.
https://doi.org/10.1137/090774823
- 22. Chen, B. and Tang, Y.C. (2019) Iterative Methods for Computing the Resolvent of the Sum of a Maximal Monotone Operator and Composite Operator with Applications. Mathematical Problems in Engineering, 2019, Article ID: 7376263.
https://doi.org/10.1155/2019/7376263






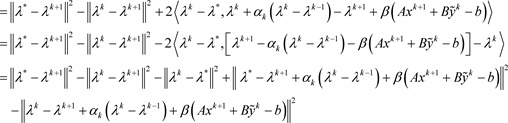
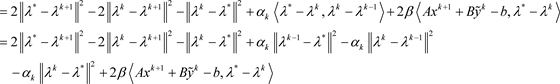 (45)
(45)
