Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18464,11
pages
10.12677/AAM.2016.53061
Subdirect Sums of Strictly Diagonally Dominant Matrices and Nekrasov Matrices
Jing Zhao, Ruiyan Hu, Yaotang Li*
School of Mathematics and Statistics, Yunnan University, Kunming Yunnan

Received: Aug. 10th, 2016; accepted: Aug. 25th, 2016; published: Aug. 31st, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
A sufficient condition ensuring that the subdirect sum of strictly diagonally dominant matrix and Nekrasov matrix is in the class of Nekrasov matrices is given. And the conclusion is illustrated by a numerical example.
Keywords:Nekrasov Matrix, Strictly Diagonally Dominant, Subdirect Sum

严格对角占优矩阵与Nekrasov矩阵的子直和
赵晶,胡汭炎,李耀堂*
云南大学数学与统计学院,云南 昆明

收稿日期:2016年8月10日;录用日期:2016年8月25日;发布日期:2016年8月31日

摘 要
给出了严格对角占优矩阵与Nekrasov矩阵的子直和为Nekrasov矩阵的充分条件,并用数值例子对所给结论进行了说明。
关键词 :Nekrasov矩阵,严格对角占优,子直和

1. 引言
矩阵在诸如微分方程,概率统计,最优化,计算数学,控制论与系统理论等数学分支都有着重要应用。1999年Fallat和Johonson引入方阵的k-子直和的概念 [1] 。由于矩阵的子直和在许多领域具有重要应用 [1] - [4] ,之后对矩阵的子直和的研究相继取得许多重要结果。2005年Pedroche和Szyld等给出两个非奇异M矩阵的子直和是非奇异M矩阵的一些充分条件 [2] ,2006年他们又给出S严格对角占优矩阵的k-子直和是S严格对角占优阵的充分条件 [5] 。2007年朱燕,黄廷祝对双对角占优矩阵的子直和进行了研究 [6] ,2010年Bru R,Cvetkovic L,Kostic V,Pedroche F对S-严格对角占优矩阵的子直和进行了研究 [7] ,2015年李朝迁,李耀堂等对Nekrasov矩阵的子直和进行了研究 [8] 。
本文我们继续研究Nekrasov矩阵的子直和,期望找到严格对角占优矩阵与Nekrasov矩阵的子直和仍为Nekrasov矩阵的条件。下面先给出本文中要用到的基本知识。
定义1.1 [1] :设A为 阶方阵,B为
阶方阵,B为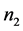 阶方阵,
阶方阵,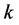 为正整数且
为正整数且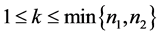 ,A和B有如下
,A和B有如下 分块形式:
分块形式:

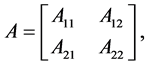 , (1)
, (1)
其中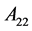 和
和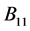 是
是 阶方阵。令
阶方阵。令
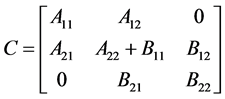 。
。
称C为A和B的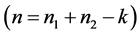
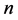 阶k-子直和,记为
阶k-子直和,记为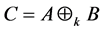 。
。
注1 [5] :设 ,
,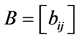 ,
,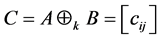 ,则由定义1.1易得:
,则由定义1.1易得:

其中
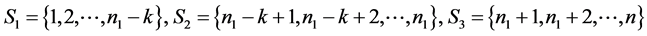 。 (2)
。 (2)
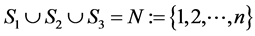 。
。
故C有可表示如下:
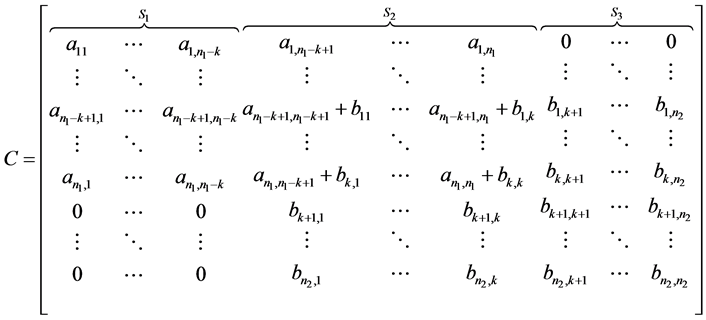 。
。
定义1.2 [9] - [11] :设矩阵 是
是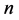 阶矩阵,若对任意一个
阶矩阵,若对任意一个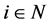 ,
,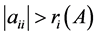 成立,其中
成立,其中 ,则称A为严格对角占优矩阵。
,则称A为严格对角占优矩阵。
定义1.3 [12] [13] :设矩阵 是
是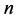 阶矩阵,令
阶矩阵,令
 ,
, 。
。
若对任意一个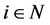 ,
,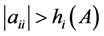 成立,则A称是Nekrasov矩阵。
成立,则A称是Nekrasov矩阵。
2. 严格对角占优矩阵与Nekrasov矩阵的子直和
首先我们用一个例子说明严格对角占优矩阵与Nekrasov矩阵的子直和不一定是Nekrasov矩阵。
例2.1:设
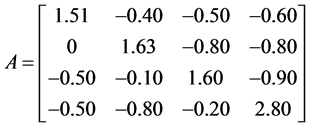 ,
,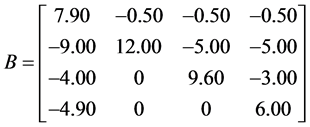 ,
,
容易验证A是严格对角占优矩阵,B是Nekrasov矩阵。由定义得A与B的3-子直和 为
为
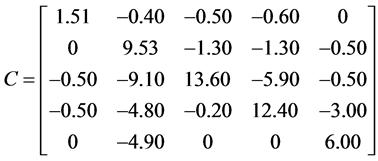 。
。
直接计算得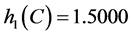 ,
,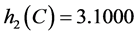 ,
, ,
,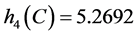 ,
,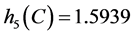 。显然,
。显然,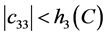 ,因此
,因此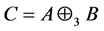 不是Nekrasov矩阵。
不是Nekrasov矩阵。
注2:例2.1表明任意给出的严格对角占优矩阵与Nekrasov矩阵的子直和不一定是Nekrasov矩阵。下面我们来寻找严格对角占优矩阵与Nekrasov矩阵的子直和是Nekrasov矩阵的条件。为此先给出三个引理。
引理2.1:设 是
是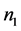 阶严格对角占优矩阵,
阶严格对角占优矩阵, 是
是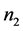 阶的Nekrasov矩阵,其分块如(1)所示,若
阶的Nekrasov矩阵,其分块如(1)所示,若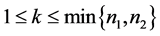 ,
,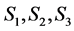 如(2)所示,其中
如(2)所示,其中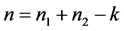 ,且
,且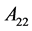 ,
,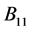 的主对角线元素全正(或全负),则对于k-子直和
的主对角线元素全正(或全负),则对于k-子直和 有:对任意的
有:对任意的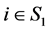 ,
,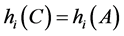 。
。
证明:该引理的结论可由注1直接得到。
引理2.2:设 是
是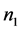 阶严格对角占优矩阵,
阶严格对角占优矩阵,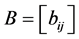 是
是 阶的Nekrasov矩阵,其分块如(1)所示,若
阶的Nekrasov矩阵,其分块如(1)所示,若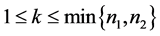 ,
,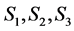 分布如(2)所示,其中
分布如(2)所示,其中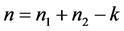 ,
,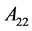 ,
,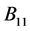 ,的主对角线元素全正(或全负),则对于k-子直和
,的主对角线元素全正(或全负),则对于k-子直和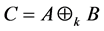 和
和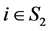 有:
有:
1)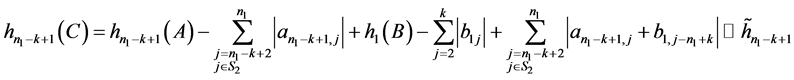 ;
;
2) 当 时:
时:
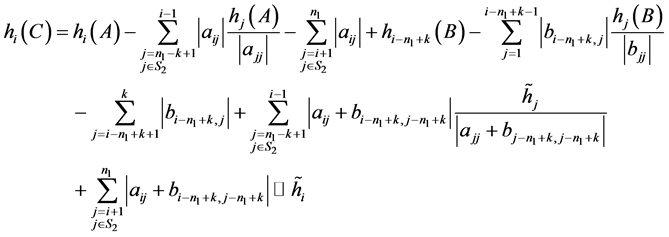 ;
;
3)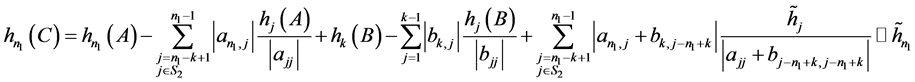 。
。
证明:设 是
是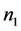 阶严格对角占优矩阵,
阶严格对角占优矩阵,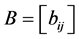 是
是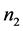 阶的Nekrasov矩阵。下面分三种情形讨论:
阶的Nekrasov矩阵。下面分三种情形讨论:
情形一:当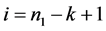 时:
时:
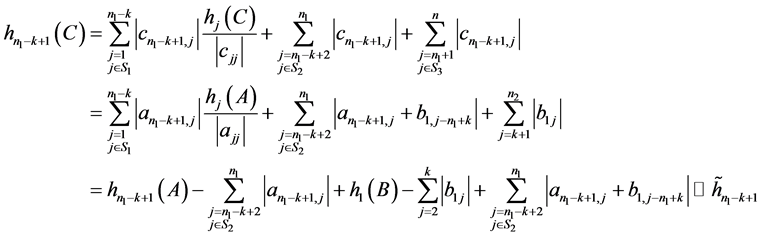 。
。
情形二:当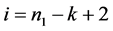 时:
时:
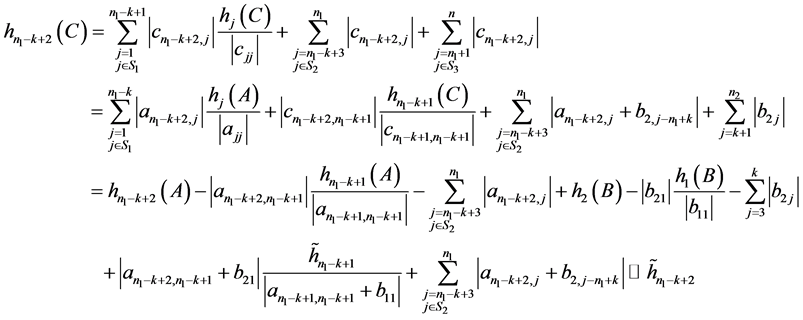 。
。
当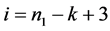 时:
时:
 。
。
现假设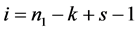 ,其中(
,其中( ),
),
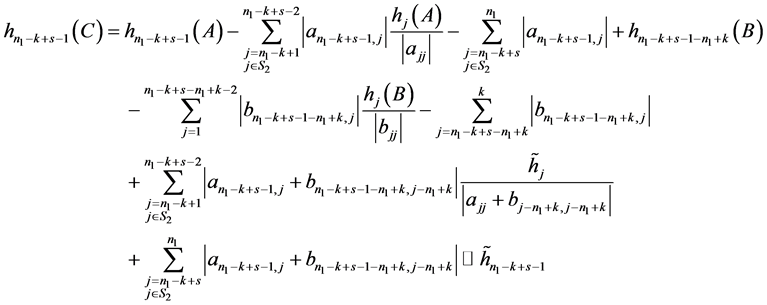 成立。
成立。
则
 。
。
情形三:当 时:
时:
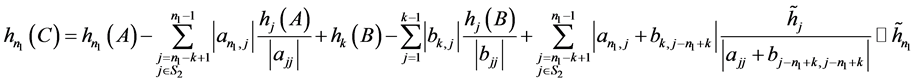 。□
。□
引理2.3:设 是
是 阶严格对角占优矩阵,
阶严格对角占优矩阵,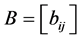 是
是 阶的Nekrasov矩阵,其分块如(1)所示,若
阶的Nekrasov矩阵,其分块如(1)所示,若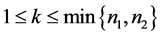 ,
,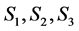 如(2)所示,其中
如(2)所示,其中 ,
,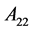 和
和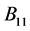 的主对角线元素全正(或全负),且
的主对角线元素全正(或全负),且
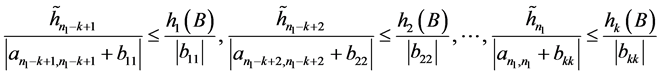 ,
,
则在A与B的k-子直和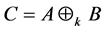 中,对任意的
中,对任意的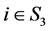 ,
,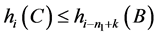 成立。
成立。
证明:我们用数学归纳法证明。设A是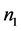 阶严格对角占优矩阵,B是
阶严格对角占优矩阵,B是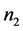 阶的Nekrasov矩阵。任取
阶的Nekrasov矩阵。任取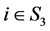 ,当
,当 时:
时:
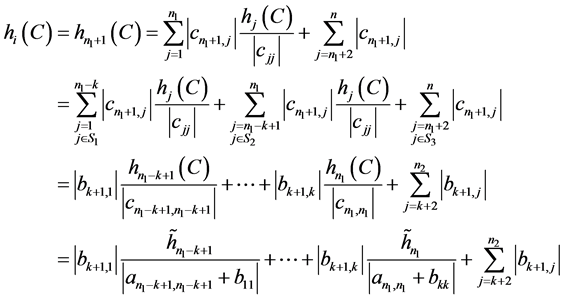 。 (3)
。 (3)
由
 。 (4)
。 (4)
和条件
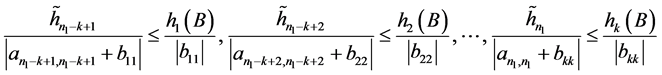 ,
,
得
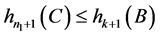 。 (5)
。 (5)
当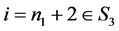 时:
时:
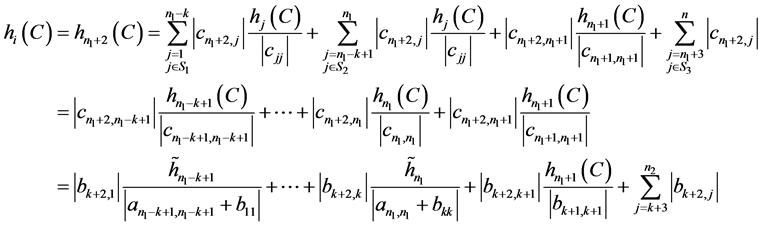 。 (6)
。 (6)
由
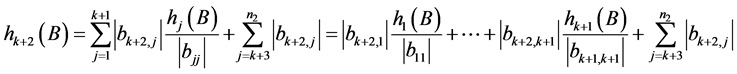 。 (7)
。 (7)
和条件
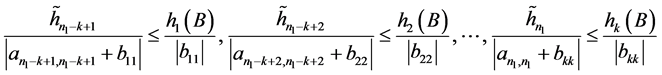 ,
,
得
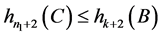 。 (8)
。 (8)
现假设任取 ,
,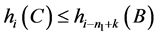 成立,下证
成立,下证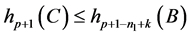 成立,其中
成立,其中 。
。
当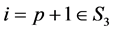 时:
时:
 。 (9)
。 (9)
由
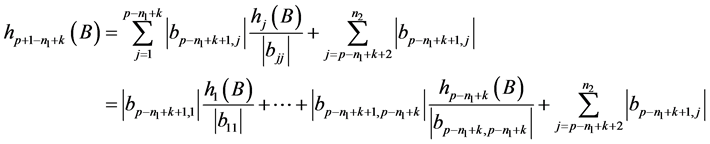 。(10)
。(10)
和条件
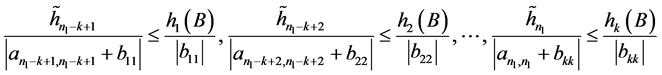 ,
,
及假设条件当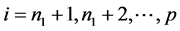 时
时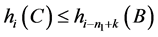 得
得
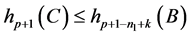 。
。
由此得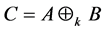 中任取
中任取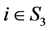 ,
,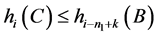 成立。□
成立。□
下面我们给出严格对角占优矩阵与Nekrasov矩阵的子直和是Nekrasov矩阵的一个充分条件。
定理2.4:设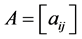 是
是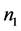 阶严格对角占优矩阵,
阶严格对角占优矩阵, 是
是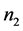 阶的Nekrasov矩阵,其分块如(1)所示,若
阶的Nekrasov矩阵,其分块如(1)所示,若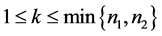 ,
,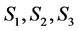 如(2)所示,其中
如(2)所示,其中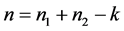 ,
,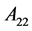 ,
,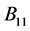 的主对角线元素全正(或全负),且
的主对角线元素全正(或全负),且
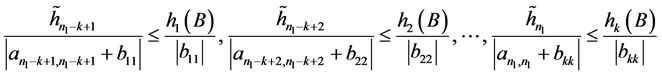 ,
,
则A与B的k-子直和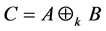 是Nekrasov矩阵。
是Nekrasov矩阵。
证明:因为A是严格对角占优矩阵,故
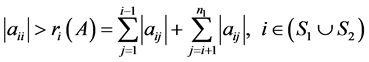 。
。
情形1:当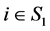 时:
时:
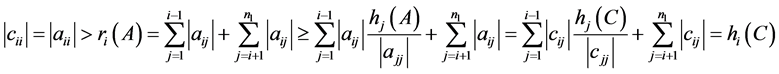 。
。
情形2:当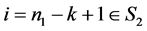 时:
时:
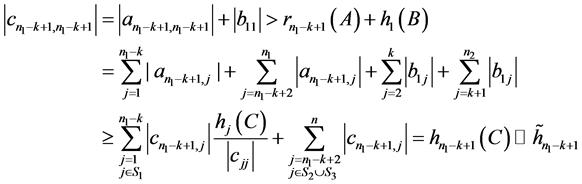 。
。
现假设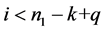 时,
时,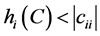 成立,则当
成立,则当 时:
时:
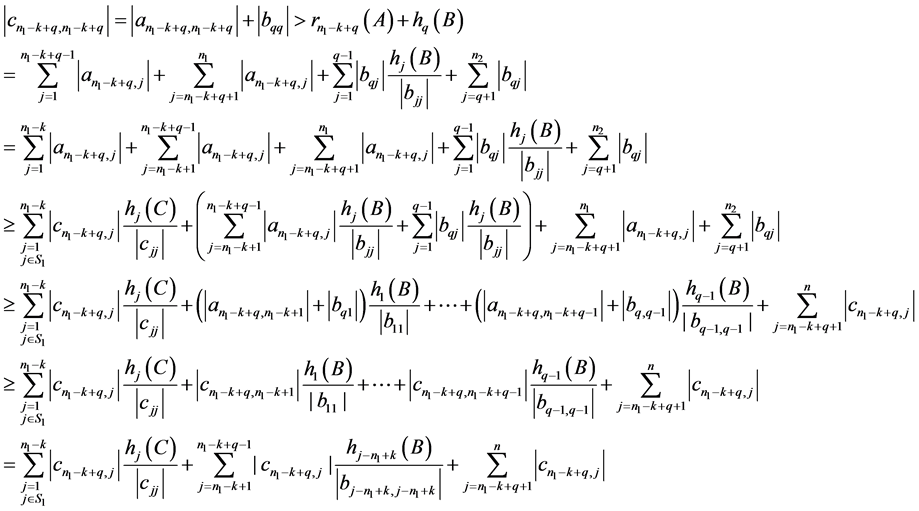 。(11)
。(11)
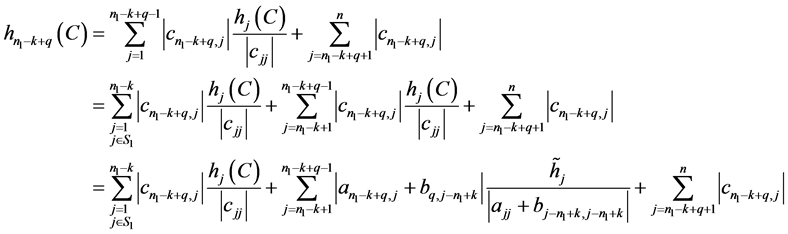 。 (12)
。 (12)
于是由条件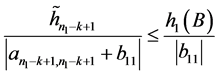 ,
,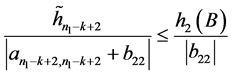 ,
, ,
,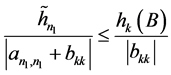 及(11)、(12)得
及(11)、(12)得
 。
。
因此对任意的 成立。
成立。
情形3:当 时:
时:
 。 (13)
。 (13)
 。 (14)
。 (14)
由条件 ,
,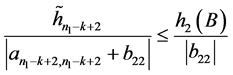 ,
, ,
,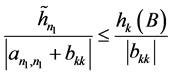 及(13)、(14)得
及(13)、(14)得
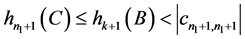 。
。
现设对任意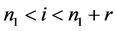 ,
, 成立,则当
成立,则当 时:
时:
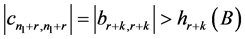 。
。
由引理2.3知对任意的 ,
, 。由此得
。由此得
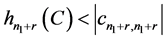 。
。
因此对任意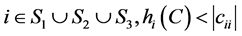 成立,从而
成立,从而 是Nekrasov矩阵。
是Nekrasov矩阵。
例2.2:设
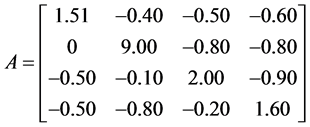 ,
,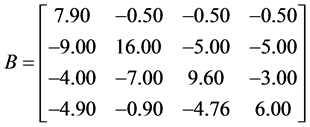 ,
,
容易验证A是严格对角占优矩阵,B是Nekrasov矩阵,于是
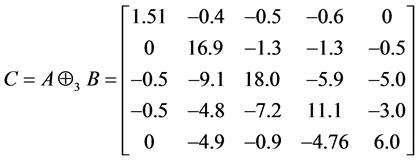 。
。
通过计算可得:
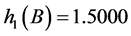 ,
,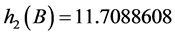 ,
,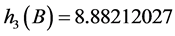 ,
,
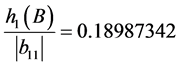 ,
, ,
,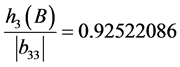 ,
,
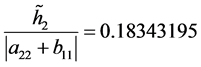 ,
, ,
,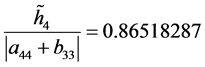 ,
,
 ,
,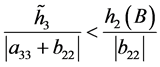 ,
,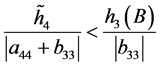 。
。
于是由定理2.4知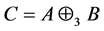 是Nekrasov矩阵。事实上,直接计算得:
是Nekrasov矩阵。事实上,直接计算得:
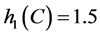 ,
,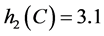 ,
,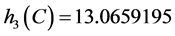 ,
, ,
,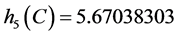 。
。
显然,当 。时
。时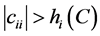 成立,因此
成立,因此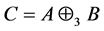 是Nekrasov矩阵。
是Nekrasov矩阵。
在定理2.4中,当k分别取1和2时得如下两个推论:
推论2.5:设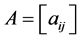 是
是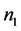 阶严格对角占优矩阵,
阶严格对角占优矩阵,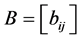 是
是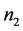 阶的Nekrasov矩阵,其分块如(1)所示,若
阶的Nekrasov矩阵,其分块如(1)所示,若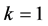 ,
, ,
,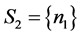 ,
,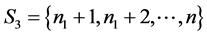 ,其中
,其中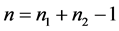 ,且
,且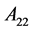 ,
,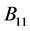 的主对角线元素全正(或全负),
的主对角线元素全正(或全负),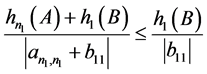 ,则
,则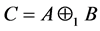 是Nekrasov矩阵。
是Nekrasov矩阵。
推论2.6:设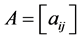 是
是 阶严格对角占优矩阵,
阶严格对角占优矩阵,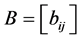 是
是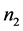 阶的Nekrasov矩阵,其分如(1)所示,
阶的Nekrasov矩阵,其分如(1)所示,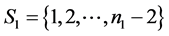 ,
, ,
,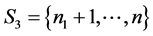 ,
,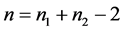 且
且 ,
, 的主对角线元素全正(或全负),
的主对角线元素全正(或全负),
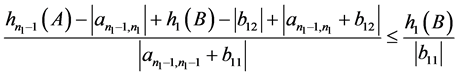 ,
,
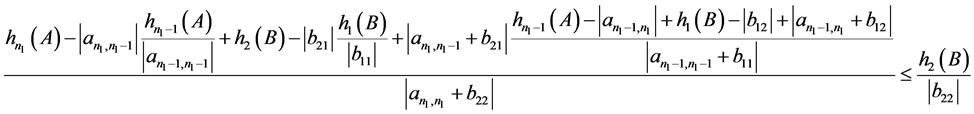 ,
,
则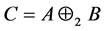 是Nekrasov矩阵。
是Nekrasov矩阵。
基金项目
本文受国家自然科学基金资助项目(11361074)资助。
文章引用
赵晶,胡汭炎,李耀堂. 严格对角占优矩阵与Nekrasov矩阵的子直和
Subdirect Sums of Strictly Diagonally Dominant Matrices and Nekrasov Matrices[J]. 应用数学进展, 2016, 05(03): 505-515. http://dx.doi.org/10.12677/AAM.2016.53061
参考文献 (References)
- 1. Fallat, S.M. and Johnson, C.R. (1999) Sub-Direct Sums and Positivity Classes of Matrices. Linear Algebra and its Applications, 288, 149-173. http://dx.doi.org/10.1016/S0024-3795(98)10194-5
- 2. Bru, R., Pedroche, F. and Szyld, D.B. (2005) Subdirect Sums of Nonsingular M-Matrices and of Their Inverse. Electronic Journal of Linear Algebra, 13, 162-174.
- 3. Frommer, A. and Szyld, D.B. (1999) Weighted Max Norms, Splittings, and Overlapping Additive Schwarz Iterations. Numerische Mathematik, 83, 259-278. http://dx.doi.org/10.1007/s002110050449
- 4. Bru, R., Pedroche, F. and Szyld, D.B. (2005) Additive Schwarz Iterations for Markov Chains. SIAM Journal on Matrix Analysis and Applications, 27, 445-458. http://dx.doi.org/10.1137/040616541
- 5. Bru, R., Pedroche, F. and Szyld, D.B. (2006) Subdirect Sums of S-Strictly Diagonally Dominant Matrices. The Electronic Journal of Linear Algebra, 15, 201-209.
- 6. Zhu, Y. and Huang, T.Z. (2007) Subdirect Sum of Doubly Diagonally Dominant Matrices. The Electronic Journal of Linear Algebra, 16, 171-182.
- 7. Bru, R., Cvetkovic, L., Kostic, V. and Pedroche, F. (2010) Sums of Strictly Diagonally Dominant Matrices. Linear and Multilinear Algebra, 58, 75-78. http://dx.doi.org/10.1080/03081080802379725
- 8. Li, C.Q., Liu, Q.L., Gao, L. and Li, Y.T. (2016) Subdirect Sums of Nekrasov Matrices. Linear Multilinear Algebra, 64, 208-218. http://dx.doi.org/10.1080/03081087.2015.1032198
- 9. Cvetkovic, L. (2006) H-Matrix Theory vs. Eigenvalue Location. Numerical Algorithms, 42, 229-245. http://dx.doi.org/10.1007/s11075-006-9029-3
- 10. Horn, R.A. and Johnson, C.R. (1985) Matrix Analysis. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511810817
- 11. Berman, A. and Plemmons, R.J. (1979) Nonnegative Matrices in the Ma-thematical Sciences. Academic Press, New York.
- 12. Li, W. (1998) On Nekrasov Matrices. Linear Algebra and its Applications, 281, 87-96. http://dx.doi.org/10.1016/S0024-3795(98)10031-9
- 13. Cvetkovic, L., Dai, P.F., Doroslovackic, K. and Li, Y.T. (2013) Infinity Norm Bounds for the Inverse of Nekrasov Matrices. Applied Mathematics and Computation, 219, 5020-5024. http://dx.doi.org/10.1016/j.amc.2012.11.056
*通讯作者。