Advances in Applied Mathematics
Vol.07 No.04(2018), Article ID:24735,10
pages
10.12677/AAM.2018.74057
An Inversion Algorithm for Inverse Coefficient Problems in the Diffusion Equation Based on Variational Adjoint Method
Zhendong Wang, Gongsheng Li, Yingmei Wang
School of Mathematics and Statistics, Shandong University of Technology, Zibo Shandong

Received: Apr. 12th, 2018; accepted: Apr. 23rd, 2018; published: Apr. 30th, 2018

ABSTRACT
A numerical inversion algorithm is proposed based on the variational adjoint method for solving the backward problem and inverse source problem in the diffusion equation. With the help of the adjoint problem, a variational identity connecting the known data with the unknown is derived with which a linear system for the unknown is set forth by suitably choosing the solution of the adjoint equation. Numerical solutions to the inverse problems are obtained by solving the linear system with Tikhonov regularization, and numerical examples are presented to demonstrate the effectiveness of the inversion algorithm.
Keywords:Diffusion Equation, Inverse Problem, Adjoint Method, Variational Identity, Numerical Inversion
基于变分伴随的扩散方程系数反问题的数值反演算法
王桢东,李功胜,王迎美
山东理工大学数学与统计学院,山东 淄博

收稿日期:2018年4月12日;录用日期:2018年4月23日;发布日期:2018年4月30日

摘 要
对于扩散方程的逆时问题与确定时间–空间依赖源项的反问题,提出一种基于变分伴随方法的数值反演算法。借助正问题的伴随问题,构建联系已知数据与未知量的变分恒等式,通过适当选择伴随方程的解进而得到关于未知量的线性方程组,结合正则化方法,获得了反问题的数值解。几个算例结果表明了这种方法的有效性。
关键词 :扩散方程,反问题,伴随方法,变分恒等式,数值反演

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
上世纪70年代以来,扩散方程/热传导方程的系数反问题一直是数学物理反问题研究的热点,主要包括反演解的条件适定性分析、数值求解及其应用研究。对于反问题的条件适定性,证明存在性的方法主要是利用不动点原理,证明惟一性与构建条件稳定性的方法主要是利用调和分析、极值原理、Carleman估计以及变分伴随等方法(见 [1] [2] [3] [4] 等)。另一方面,对于反问题的数值求解研究,一般是基于最优化理论与正则化方法构建稳定的数值迭代方法(见专著 [5] [6] [7] [8] [9] 等)。反演算法实施中要多次迭代求解正问题,因而计算量相对较大、计算成本高。
对于热传导方程/扩散方程系数反演问题的研究,Cannon [10] 与Beck [11] 均有开创性的工作。最近,刘进贤教授提出了不需要反复求解正问题的Trefftz型反演方法(见 [12] [13] [14] 等)。这类方法对于线性热传导方程的确定初始函数、边值函数或源项系数的参数反演问题,基于边界–区域积分方程和Green公式,利用附加数据和相容性条件,通过选取试验函数得到一类带辅助参数的线性方程组,进而应用梯度类算法获得反问题的数值解。
本文考虑扩散方程的逆时问题与源项反问题的数值反演。应用变分伴随方法,建立联系已知数据函数与未知量的变分恒等式。通过适当选择伴随方程的解获得变分恒等式的离散形式,进而结合Tikhonov正则化实现有效的数值反演。文中主要内容的安排是:第2节给出文中讨论的正问题与参数反演问题,第3节构建一个联系已知与未知的变分恒等式,并提出相应的反演算法,第4节给出几个数值算例,验证反演算法的有效性,最后一节给出结论。
2. 正问题与反问题
2.1. 正问题
设 是带有(分片)光滑边界的有界开区域。对于
是带有(分片)光滑边界的有界开区域。对于 ,记
,记 ,
, ,G为W的边界。考虑线性扩散方程:
,G为W的边界。考虑线性扩散方程:
 (2.1)
(2.1)
其中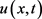 表示空间点x处与时刻t时的状态分布,
表示空间点x处与时刻t时的状态分布,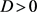 是扩散系数,
是扩散系数,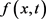 表示源/汇项。给定初边值条件给定为
表示源/汇项。给定初边值条件给定为
 (2.2)
(2.2)
及
 (2.3)
(2.3)
如果正问题(2.1)~(2.3)中的模型参数与初边值函数都是已知的且属于适当的函数空间,则正问题是适定的且在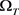 上存在唯一解。有关正问题适定性的论断可参见标准的偏微分方程教材,本文主要讨论两个基于(2.1)~(2.3)的反问题的数值反演。
上存在唯一解。有关正问题适定性的论断可参见标准的偏微分方程教材,本文主要讨论两个基于(2.1)~(2.3)的反问题的数值反演。
2.2. 逆时问题与源项反问题
假设正问题模型中的边值函数与源项都是已知的,则逆时问题是给定某个 时刻的终值观测数据,确定初始分布函数
时刻的终值观测数据,确定初始分布函数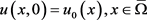 。换言之,给定附加条件,
。换言之,给定附加条件,
 (2.4)
(2.4)
逆时问题是基于(2.1)~(2.3),由 确定
确定 。
。
如果正问题(2.1)~(2.3)中的初边值函数都是已知的,则源项反问题是利用解的部分附加信息确定 。这时,由于源项函数既依赖时间变量同时又依赖空间变量,单纯由终值数据条件(2.4)难以唯一确定时间–空间依赖的源项函数。根据边值条件(2.3),再补充Neumann边界数据条件
。这时,由于源项函数既依赖时间变量同时又依赖空间变量,单纯由终值数据条件(2.4)难以唯一确定时间–空间依赖的源项函数。根据边值条件(2.3),再补充Neumann边界数据条件
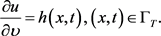 (2.5)
(2.5)
其中v表示边界点处的单位外法向量。以下考虑的源项反问题即是基于正问题(2.1)~(2.3),由附加条件(2.4)~(2.5)确定源项 。
。
下面基于一个联系已知数据与未知参数的变分恒等式,给出上述两类反问题的数值求解方法,并结合正则化策略进行数值反演。
3. 变分恒等式与反演算法
3.1. 变分恒等式
基于正问题(2.1)~(2.3),通过对其伴随问题解的控制,可以构建一个联系已知与未知的变分恒等式,这是一类边界-区域积分方程。
定理1:设 ,
, ,且
,且 ,则成立变分恒等式:
,则成立变分恒等式:
 (3.1)
(3.1)
其中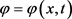 是下述伴随问题的解
是下述伴随问题的解
 (3.2)
(3.2)
这里初值 与边界输入
与边界输入 均为可控制的已知函数。
均为可控制的已知函数。
证明:记选择光滑试验函数 乘以方程(2.1)的两边,并在
乘以方程(2.1)的两边,并在 上积分,可得
上积分,可得
 (3.3)
(3.3)
首先,由分部积分可知
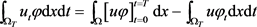 (3.4)
(3.4)
其次,利用Green公式可得

对上式左边各项分部积分,利用(3.3)中的零初值条件,可得
 (3.5)
(3.5)
令 是伴随问题(3.2)的解,则将式(3.4)与(3.5)代入(3.3),并注意到初始函数与终值数据,整理即得(3.1)。证毕。
是伴随问题(3.2)的解,则将式(3.4)与(3.5)代入(3.3),并注意到初始函数与终值数据,整理即得(3.1)。证毕。
3.2. 反演算法
本小节以逆时问题为例,基于变分恒等式(3.1)给出反演算法。不妨设区域内没有源项作用,即设模型中的源项 。则变分恒等式(3.1)简化为
。则变分恒等式(3.1)简化为
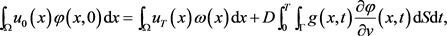 (3.6)
(3.6)
其中在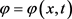 在
在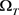 上满足方程
上满足方程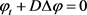 及齐次边值条件,且有
及齐次边值条件,且有 。根据Laplace算子的性质,存在完备的特征系统
。根据Laplace算子的性质,存在完备的特征系统 ,伴随问题的解具有广义Fourier展开形式
,伴随问题的解具有广义Fourier展开形式
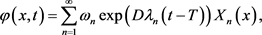 (3.7)
(3.7)
其中 ,是
,是 在W上的Fourier展开系数。
在W上的Fourier展开系数。
对于常数 ,记
,记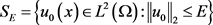 为初始函数的容许集合。则存在一组基
为初始函数的容许集合。则存在一组基 ,有展开式
,有展开式
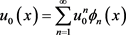 (3.8)
(3.8)
其中 称为展开系数。若取有限项近似,则有
称为展开系数。若取有限项近似,则有
 (3.9)
(3.9)
再注意到(3.7)式,可选取适当的 及相应伴随问题的解
及相应伴随问题的解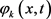 ,并依次代入恒等式(3.6),得到
,并依次代入恒等式(3.6),得到
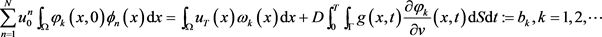 (3.10)
(3.10)
记
 (3.11)
(3.11)
及
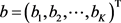
可得一个线性系统
 (3.12)
(3.12)
由于系数矩阵G的病态性,以及观测数据误差与计算误差的作用,通常需要采用正则化策略求解方程(3.12)的扰动形式:
 (3.13)
(3.13)
这里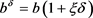 ,x为分布于[−1,1]的随机数,
,x为分布于[−1,1]的随机数,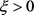 为扰动水平。根据Tikhonov正则化,适当选取正则参数
为扰动水平。根据Tikhonov正则化,适当选取正则参数 ,则初始函数有限逼近部分的系数由下式近似计算
,则初始函数有限逼近部分的系数由下式近似计算
 (3.14)
(3.14)
注1:在具体的算法实施中,可以利用数据的相容性等条件,降低系统(3.12)~(3.13)的病态性。此外,由于这种反演算法不需要迭代过程,多数情况下只要先验选取正则参数,就可以获得稳定的数值解。
注2:该算法依赖于截断项数N与K的选取。从(3.9)式看出,当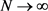 时,近似解逼近真解;另一方面,K的大小意味着附加信息量的多少,理论上也是越大越好。关于这些讨论以及数值解的收敛性分析都是重要的问题,我们将另文再表。
时,近似解逼近真解;另一方面,K的大小意味着附加信息量的多少,理论上也是越大越好。关于这些讨论以及数值解的收敛性分析都是重要的问题,我们将另文再表。
4. 数值反演
4.1. 逆时问题的数值反演
考虑一维齐次扩散方程 在第一边值条件下的逆时问题。
在第一边值条件下的逆时问题。
算例1:设研究区域 ,终值时刻
,终值时刻 ,且正问题的真解为
,且正问题的真解为 。则两个边值函数分别为
。则两个边值函数分别为 及
及 ;无扰动的终值数据为
;无扰动的终值数据为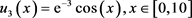 。假设初始分布函数具有近似表达式
。假设初始分布函数具有近似表达式
 (4.1)
(4.1)
这里数值反演即是求解向量 。
。
对于伴随方程 ,取其解为
,取其解为
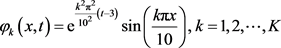 (4.2)
(4.2)
而 。取
。取 ,利用上一节所述的反演方法进行直接计算。图1绘制了
,利用上一节所述的反演方法进行直接计算。图1绘制了
采用精确数据的反演解与精确解;图2(a),图2(b)分别绘制了扰动水平时 与
与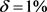 时的反演解与精确解,其中正则参数均取
时的反演解与精确解,其中正则参数均取 。
。
算例2:设研究区域 ,终值时刻
,终值时刻 ,且正问题的真解为
,且正问题的真解为 。则两个边值函数分别为
。则两个边值函数分别为 及
及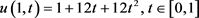 ,无扰动的终值数据为
,无扰动的终值数据为 。这里初始分布函数仍沿用(4.1)近似表达式。类似于算例1中的计算,取
。这里初始分布函数仍沿用(4.1)近似表达式。类似于算例1中的计算,取 ,正则参数
,正则参数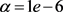 ,图3(a),图3(b)分别绘制了扰动水平时
,图3(a),图3(b)分别绘制了扰动水平时 与
与 时的反演解与精确解。
时的反演解与精确解。

Figure 1. Inversion result for the backward problem with accurate data in Ex.1.
图1. 算例1中精确数据下逆时问题的反演结果,

Figure 2. Inversion result for the backward problem with noisy data in Ex.1. (a) ; (b)
; (b) 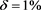
图2. 算例1中扰动数据下逆时问题的反演结果,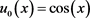 。(a)
。(a) ;(b)
;(b) 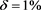
4.2. 源项的数值反演
考虑一维非齐次扩散方程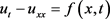 在第一边值条件下的源项反问题。
在第一边值条件下的源项反问题。
算例3:设研究区域 ,终值时刻
,终值时刻 ,正问题的真解为
,正问题的真解为 ,而源项真解为
,而源项真解为 。正问题的两个边值函数分别为
。正问题的两个边值函数分别为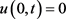 及
及 。终值附加数据为
。终值附加数据为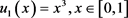 。根据第2节的论述,还需要两个边界处的Neumann附加数据
。根据第2节的论述,还需要两个边界处的Neumann附加数据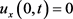 及
及 ,
, 。
。
假设源项具有近似表达式
 (4.3)
(4.3)

Figure 3. Inversion results for the backward problem with noisy data in Ex.2. (a)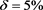 ; (b)
; (b) 
图3. 算例2中扰动数据下逆时问题的反演结果, 。(a)
。(a) ;(b)
;(b) 

Figure 4. Exact source and inversion source solutions with accurate data in Ex.3. (a) Exact source; (b) Inversion source with accurate data
图4. 算例3中源项真解与精确数据下的反演解, 。(a) 源项真解;(b)
。(a) 源项真解;(b) 时的反演解
时的反演解
数值反演即是求解向量 。注意到时空依赖源项反问题的病态性,对于
。注意到时空依赖源项反问题的病态性,对于 ,取伴随方程的两个解:
,取伴随方程的两个解:
 (4.4)
(4.4)
其中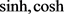 分别为双曲正弦、余弦函数,
分别为双曲正弦、余弦函数, 为调节参数。取
为调节参数。取 及
及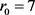 ,利用所述的反演方法进行直接计算。图4(a),图4(b)分别绘制了源项真解与采用精确数据的反演解;图5(a),图5(b)分别绘制了扰动水平
,利用所述的反演方法进行直接计算。图4(a),图4(b)分别绘制了源项真解与采用精确数据的反演解;图5(a),图5(b)分别绘制了扰动水平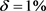 与
与 时的反演解与真解,其中正则参数分别取
时的反演解与真解,其中正则参数分别取 与
与 。
。
算例4:继续考虑区域 ,终值时刻
,终值时刻 ,而正问题的真解为
,而正问题的真解为 ,源项真解为
,源项真解为 。正问题的两个边值函数分别为
。正问题的两个边值函数分别为 及
及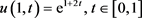 ;终值附加数据为
;终值附加数据为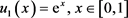 。另外,两个端点处的Neumann边界数据为
。另外,两个端点处的Neumann边界数据为 及
及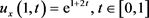 。
。
假设源项仍具有(4.3)式的近似表达式,且反演参数也同于算例3中所取,图6(a),图6(b)分别绘制了源项真解与采用精确数据的反演解;图7(a),图7(b)分别绘制了扰动水平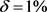 与
与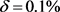 时的反演解与真解,其中正则参数分别取
时的反演解与真解,其中正则参数分别取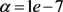 与
与 。
。
5. 结论
本文对于扩散方程/热方程的逆时问题与源项反问题,基于变分伴随方法,建立了一类联系已知数据

Figure 5. The inversion source solutions with noisy data in Ex.3. (a) ; (b)
; (b) 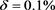
图5. 算例3中扰动数据下的源项反演解。(a) ;(b)
;(b) 

Figure 6. Exact source and the inversion source solutions with accurate data in Ex.4. (a) Exact source; (b) Inversion source solution with accurate data
图6. 算例4中源项真解与精确数据下的反演解, 。(a) 源项真解;(b)
。(a) 源项真解;(b) 时的反演解
时的反演解

Figure 7. Inversion source solutions with noisy data in Ex.4. (a) ; (b)
; (b) 
图7. 算例4中扰动数据下的源项反演解。(a)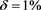 ;(b)
;(b) 
函数与未知量的积分恒等式,通过适当选取伴随方程的解并结合Tikhonov正则化实现了参数的有效反演。这种反演方法推广并简化了Trefftz型参数反演算法,可适用于一般线性数理方程系数反问题的数值求解。
基金项目
国家自然科学基金资助项目(No. 11371231)。
致谢
感谢审稿人提出的修改意见。
文章引用
王桢东,李功胜,王迎美. 基于变分伴随的扩散方程系数反问题的数值反演算法
An Inversion Algorithm for Inverse Coefficient Problems in the Diffusion Equation Based on Variational Adjoint Method[J]. 应用数学进展, 2018, 07(04): 466-475. https://doi.org/10.12677/AAM.2018.74057
参考文献
- 1. Cheng, J. and Yamamoto, M. (2000) The Global Uniqueness for Determining Two Convection Coefficients from Dirichlet to Neumann Map in Two Dimensions. Inverse Problems, 16, L25-L30. https://doi.org/10.1088/0266-5611/16/3/101
- 2. DuChateau, P. (2013) An Adjoint Method for Proving Identifiability of Coefficients in Parabolic Equations. Journal of Inverse and Ill-Posed Problems, 21, 639-663. https://doi.org/10.1515/jip-2013-0010
- 3. Isakov, V. (1998) Inverse Problems for Partial Differential Equations. Springer, New York. https://doi.org/10.1007/978-1-4899-0030-2
- 4. Yamamoto, M. (2009) Carleman Estimates for Parabolic Equations and Applications. Inverse Problems, 25, 123013. https://doi.org/10.1088/0266-5611/25/12/123013
- 5. Tikhonov, A.N., Goncharsky, A.V., Stepanov, V.V. and Yagola, A. (1995) Numerical Methods for the Solution of Ill-Posed Problems. Kluwer, Dordrecht. https://doi.org/10.1007/978-94-015-8480-7
- 6. Engl, H.W., Hanke, M. and Neubauer, A. (1996) Regularization of Inverse Problems. Kluwer Academic, Dordrecht. https://doi.org/10.1007/978-94-009-1740-8
- 7. 刘继军. 不适定问题的正则化方法及应用[M]. 北京: 科学出版社, 2005.
- 8. 王彦飞. 反演问题的计算方法及其应用[M]. 北京: 高等教育出版社, 2007.
- 9. 韩波, 李莉. 非线性不适定问题的求解方法及其应用[M]. 北京: 科学出版社, 2011.
- 10. Cannon, J.R. (1984) The One Dimensional Heat Equation. Addison-Wesley, London.
- 11. Beck, J.V., Blackwell, B. and St. Clair, C.R. (1985) Inverse Heat Conduction: Ill-Posed Problems. Wiley-Interscience, New York.
- 12. Liu, C.-S. and Wang, P.F. (2016) An Analytic Adjoint Trefftz Method for Solving the Singular Parabolic Convection-Diffusion Equation and Initial Pollution Profile Problem. International Journal of Heat and Mass Transfer, 101, 1177-1184. https://doi.org/10.1016/j.ijheatmasstransfer.2016.05.134
- 13. Liu, C.-S. (2016) A Simple Trefftz Method for Solving the Cauchy Problems of Three-Dimensional Helmholtz Equation. Engineering Analysis with Boundary Elements, 63, 105-113. https://doi.org/10.1016/j.enganabound.2015.11.009
- 14. Liu, C.-S, Qu, W.Z. and Zhang, Y.M. (2018) Numerically Solving Twofold Ill-Posed Inverse Problems of Heat Equation by the Adjoint Trefftz Method. Numerical Heat Transfer: Part B, 73, 48-61. https://doi.org/10.1080/10407790.2017.1420317