Advances in Applied Mathematics
Vol.
08
No.
03
(
2019
), Article ID:
29440
,
6
pages
10.12677/AAM.2019.83063
Wiener Index of Complements of Line Graphs
Xiaohong Chen, Zhonghua Li, Xinhui An
College of Mathematics and System Science, Xinjiang University, Urumqi Xinjiang

Received: Mar. 5th, 2019; accepted: Mar. 20th, 2019; published: Mar. 27th, 2019

ABSTRACT
Let G be a graph of size q ≥ 1. The jump graph J(G) of G is the complement of the line graph L(G) of G. The Wiener index W(G) of G is the sum of the distances between all pairs of vertices in G. In this paper, we determine the Wiener index of J(G), where J(G) is connected.
Keywords:Line Graphs, Jump Graph, Wiener Index
线图的补图的Wiener指标
陈小红,李中华,安新慧
新疆大学,数学与系统科学学院,新疆 乌鲁木齐

收稿日期:2019年3月5日;录用日期:2019年3月20日;发布日期:2019年3月27日

摘 要
令G是一个边数不小于1的图。我们称图G的线图L(G)的补图为跳图,记作J(G)。图G的Wiener指标是图G中所有点对的距离之和。在本文中,我们确定了图J(G)的Wiener指标,其中图J(G)是连通的。
关键词 :线图,跳图,Wiener指标

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本篇文章中所有的图都限定为无向的简单图。相关的术语和符号可以参考文献 [1] 。设
是一个简单图,其中 是图G的顶点集, 是图G的边集,我们分别用 和 记作 和 的阶。通常我们用 表示阶为n的路。对于 中的每一个点v,用 表示与点v相邻的所有顶点的集合,称为v的邻点集。 称为点v的度数。一般地,我们用 表示H是图G的一个子图或者表示H同构于G中的一个子图。
在一个连通图G中,记 为G中任意两个点 和v之间的距离(两点之间最短路的长度), 为图G的Wiener指标,定义为 。
这个概念最初是由Harry Wiener在文献 [2] 中提到的。从那时起,许多研究者对Wiener指标进行了广泛的研究。关于一些Wiener指标的化学应用和数学研究的调查可以参考文献 [3] [4] 以及其中引用的参考资料。
为图G的线图,其中 并且对于任意两个点在 中相邻当且仅当这两个点对应的边在G中相邻。 为图G的补图,其中 并且对于任意两个点u和v在 中相邻当且仅当u和v在G中不相邻。在文献 [5] 中Chartrand等研究者称线图的补图为跳图,记作 并且给出了
一些跳图是哈密顿的充分条件。吴和孟在文献 [6] 中给出了一些哈密顿跳图的结构。我们可以在文献 [7] [8] [9] [10] 中查阅到线图的补图的更多结果。
在文献 [5] 中Chartrand等研究者证明了如果一个跳图 是连通的,则它的直径不超过4。在文献 [2] 中吴和郭给出了跳图的直径r在1到4之间的原图G的结构。在本文中,我们将根据吴和郭的结果确定连通的跳图 的Wiener指标。
2. 主要内容
2.1. 预备知识
在文献 [5] 中Chartrand等人给出了下面的结果。
定理2.1.1 [5] 如果 是连通的,则 。
在文献 [2] 中吴和郭根据上面的结果给出了下面的定理。
定理2.1.2 [2] 对于一个边数不小于1的图G,如果 是连通的,则:
1) 当且仅当 ;
2) 当且仅当:
a) G包含一个子图 , 是由给 中的点u加一个新的邻点,
b) 如果G中存在一条边关联v或x,则这条边必须是vx。此外,如果 ,则 ,
c) G中任意一条除 以外的边都与u关联;
3) 当且仅当:
a) G包含 ,
b) 对于G中任意一条不在 上的边必有一个端点在 的2度顶点上,
c) 同时G不满足(2)中的情况;
4) ,其他。
在本文,我们主要根据上面对线图的补图的刻画来计算线图的补图的Wiener指标。
2.2. 直径小于等于2
引理2.2.1 如果 ,, ,则 。
证明:因为 ,所以对于任意的点 ,u和v之间的距离为1或2。因此
.
定理2.2.2对于一个边数为m的图G,如果 ,则
证明:因为 ,所以
,
其中 。
所以由引理2.2.1知:
.
2.3. 直径等于3
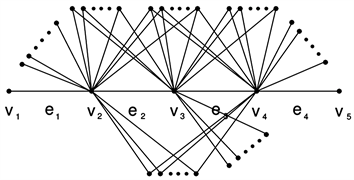
由定理2.1.2知:当 ,则图G的结构如图1所示。
令 和 分别作为 的顶点集和边集,且 ,。假设 ,, 并且 ,, ,显然 ,,。
定理2.3.1对于一个边数为m的图G,如果 ,则
,
其中 且 。
图1.
证明:首先 。
如果 ,对于任意边 且 ,则在 中 到 ,,, 的距离之和为6。令 且 。有
,
其中 。
现在我们来计算 :
对于任意边 和 其中 ,则 。因此
.
对于任意边 ,则 。因此
.
对于任意边 ,则 。因此
.
对于任意边 ,则 。因此
.
综上所述:
.
因此
.
2.4. 直径等于4
由定理2.1.2知:当 ,G有三种结构形式 和 ,如图2所示。
, .
, .
, .

Figure 2. and
图2. 和
定理2.4.1 对于一个点数为n的图G,如果 ,则
证明:对于任意图G,如果
,则对于任意边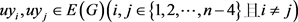 ,有
。因此
,有
。因此
.
对于任意边 ,则 。因此
.
对于任意边 ,显然 。因此
.
同理, ,,,。
综上所述:
.
根据上面的方法我们得到,若 或 ,有
基金项目
国家自然科学基金青年科学基金(NO. 11801487)。
文章引用
陈小红,李中华,安新慧. 线图的补图的Wiener指标
Wiener Index of Complements of Line Graphs[J]. 应用数学进展, 2019, 08(03): 569-574. https://doi.org/10.12677/AAM.2019.83063
参考文献
- 1. Dobrynin, A.A., Entringer, R. and Gutman, I. (2001) Wiener Index of Trees: Theory and Applications. Acta Applicandae Mathematicae, 66, 211-249. https://doi.org/10.1023/A:1010767517079
- 2. An, X. and Wu, B. (2007) Ham-iltonicity of Complements of Middle Graphs. Discrete Mathematics, 307, 1178-1184. https://doi.org/10.1016/j.disc.2006.07.028
- 3. Bondy, J.A. and Murty, U.S.R. (1976) Graph Theory with Appli-cations. American Elsevier, New York, Macmillan, London. https://doi.org/10.1007/978-1-349-03521-2
- 4. Chen, X., Liu, J., Xie, D. and Meng, J. (2016) Edge Connectivity and Super Edge-Connectivity of Jump Graphs. Information and Optimization Sciences, 37, 233-246. https://doi.org/10.1080/02522667.2015.1103062
- 5. Chartrand, G., Hevia, H., Jarrett, E.B. and Schultz, M. (1997) Subgraph Distances in Graphs Defind by Edge Transfers. Discrete Mathematics, 170, 63-79. https://doi.org/10.1016/0012-365X(95)00357-3
- 6. Gutman, I. and Körtvelyesia, T. (1995) Wiener Indices and Molecular Surfaces. Zeitschrift für Naturforschung, 50, 669-671.
- 7. Knor, M., Skrekovski, R. and Tepeh, A. (2015) Mathematical Aspects of Wiener Index. Graphs and Combinatorics, 29, 1403-1416.
- 8. Wu, B. and Meng, J. (2004) Hamiltonian Jump Graphs. Discrete Mathematics, 289, 95-106. https://doi.org/10.1016/j.disc.2004.09.003
- 9. Wu, B. and Guo, X. (2001) Diameters of Jump Graphs and Self-Complementary Jump Graphs. Graph Theory Notes of New York, 40, 31-34.
- 10. Wu, B., Liu, X. and Guo, X. (2008) Super-Connected and Hyper-Connected Jump Graphs. International Journal of Computer Mathematics, 85, 1765-1769. https://doi.org/10.1080/00207160701600069