Advances in Applied Mathematics
Vol.
09
No.
03
(
2020
), Article ID:
34782
,
7
pages
10.12677/AAM.2020.93053
Oscillation of a Class of Third-Order Semilinear Delay Differential Equations
Dan Li1, Chunzhi Chen1, Jingjie Lin1*, Liangtian Zheng2
1Department of Mathematics and Applied Mathematics, School of Science, Guangdong University of Petrochemical Technology, Maoming Guangdong
2Department of Electrical Engineering, College of Automation, Guangdong University of Petrochemical Technology, Maoming Guangdong
Received: Mar. 4th, 2020; accepted: Mar. 20th, 2020; published: Mar. 27th, 2020

ABSTRACT
The oscillation of a class of third-order semilinear differential equations is studied. Different functions are constructed using Riccati transformation techniques and classical inequalities. Some new oscillation criteria and asymptotic properties of this type of differential equations are established. The conclusions are generalized and improved. Some related results in the literature are given, and examples are used to illustrate the advanced nature of the results.
Keywords:Oscillation, Delay Differential Equation, Semilinear

一类三阶半线性时滞微分方程的振动性
李丹1,陈淳智1,林靖杰1*,郑量天2
1广东石油化工学院理学院数学与应用数学系,广东 茂名
2广东石油化工学院自动化学院电气工程系,广东 茂名

收稿日期:2020年3月4日;录用日期:2020年3月20日;发布日期:2020年3月27日

摘 要
研究了一类的三阶半线性微分方程的振动性,应用Riccati变换技巧和经典不等式等方法构造不同的函数,建立该类微分方程的一些新的振动准则和渐近性,所得结论推广和改进了文献中的某些相关结果,并以例子说明结果的先进性。
关键词 :振动性,时滞微分方程,半线性

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
考虑如下一类三阶半线性时滞微分方程
(E)
的振动性。
假设以下条件都成立
一般来说,若连续可微函数 在定义域内是满足方程(E)有无穷多个零点的解,则说方程(E)是振动
的;若方程最终是一个正解或者负解,则说方程(E)是非振动的。对于 ,若 ,
则称它是正则的,否则为收敛。
最近几年,微分方程这一理论在应用数学领域中已取得了迅速的发展和广泛的应用,他可以描述金融、经济、化学反应过程的稳定性的研究、飞机和导弹飞行的稳定性的研究、人口统计、传播传染病过程等问题。很多学者对三阶半线性微分方程的振动性做了深入的研究,同时也获得了许多成果,如文 [1] - [13]。
在2017年,在文献 [2] 中,建立了方程(E)的所有解振动或者收敛到零的若干新的振动准则如下:
定理A:假设条件(H1)~(H5)及(3) [2] 式成立,如果
则式(1)的解 振动,或者 。
定理B:假设条件(H1)~(H5)及(3) [2] 式成立,如果
则式(1)的解 振动,或者 。
最近文献 [13] 研究了式(1)在 情况下的振动性,得到的主要结果有:
定理C:若存在函数 ,满足 和(2.1) [13] 式,且
则式(1)的解 振动,或者当 时, 。
定理D:若存在函数 ,使(2.1) [13] 式成立,且满足
则式(1)的解 振动,或者当 时, 。
本文研究了方程(E)的振动性准则,参考了文献 [1] [2] [9] [10] [11] [12],在文献 [2] [9] [13] 的启发下,应用Riccati变换和经典不等式等方法构造不同的函数,建立该类微分方程的一些新的振动性理论,获得合理的结果,并将举例说明主要结果的应用及其先进性。
引理1 [1]:如果 是方程(E)的非振动正解,则 只有以下两种情况:
1) ;
2) 。
引理2 [2]:设 是方程(E)的非振动正解,且 ,则
其中 。
证明:由 ,可得 ,利用条件(H2),(H3)及 可得,
(1)
根据(1)和方程(E)可得
其中 。
引理3 [9]:存在 ,假设 为方程(E)在 上的一个非振动正解,满足 ,且有
则有 。
引理4 [10]:设 ,则对任一 ,存在 ,使得 。
引理5 [11]:假设
,则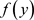 当且仅当
当且仅当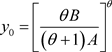 处有最大值
处有最大值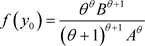 .
.
引理6设存在 ,
,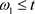 ,假设
,假设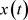 为方程(E)在
为方程(E)在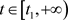 上的一个非振动正解,满足
上的一个非振动正解,满足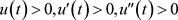 ,则对任一
,则对任一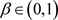 ,存在
,存在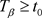 ,使得
,使得
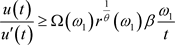
证明:由于 ,
, ,则有
,则有
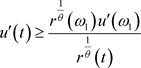 (2)
(2)
将(2)在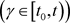
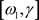 上对t积分,且令
上对t积分,且令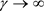 ,得
,得
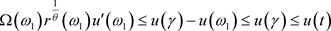 (3)
(3)
由引理4,令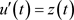 ,对任一
,对任一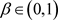 ,存在
,存在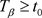 ,使得
,使得
 (4)
(4)
将(4)代入(3)中,得

即
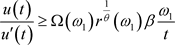 (5)
(5)
2. 主要结果
定理2.1:如果存在函数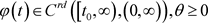 ,
,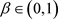 满足
满足
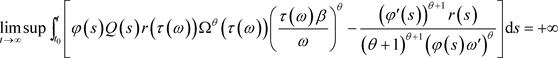 (6)
(6)
和
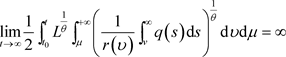 (7)
(7)
其中,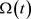 是正则的,
是正则的,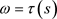 ,则方程(E)是振动的或者
,则方程(E)是振动的或者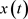 最终趋于0。
最终趋于0。
证明:不失一般性,存在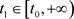 ,不妨设
,不妨设 为方程(E)在
为方程(E)在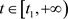 上的一个非振动正解。由引理1可知,结果只有两种情况。若满足
上的一个非振动正解。由引理1可知,结果只有两种情况。若满足 第一种情况,则方程(E)可变成
第一种情况,则方程(E)可变成
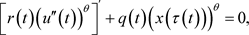
由广义Riccati变换得
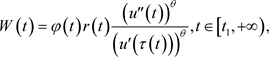
根据求导性质可得
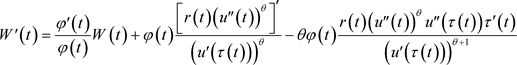
由于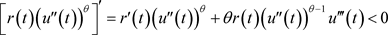 ,
,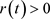 ,
,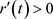 ,
,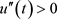 ,可得
,可得 ,从而可得
,从而可得
 (8)
(8)
由引理2和(8)得
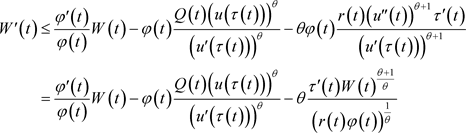 (9)
(9)
由引理6得,令 ,对任一
,对任一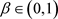 ,存在
,存在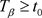 ,使得
,使得
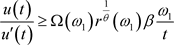 (10)
(10)
将(10)代入(9),可得
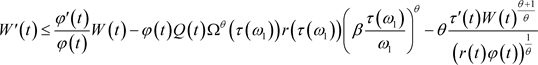 (11)
(11)
令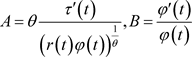 ,由引理5,可得
,由引理5,可得

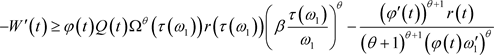 (12)
(12)
对(12)从 上对s积分,其中
上对s积分,其中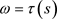 ,有
,有
 (13)
(13)
显然,式(13)与条件(6)矛盾;因此,当满足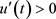 时,方程(E)是振动的。若满足
时,方程(E)是振动的。若满足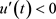 情况,由引理3可知,
情况,由引理3可知,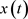 最终趋于0,定理得证。
最终趋于0,定理得证。
3. 例子
例考虑三阶微分方程
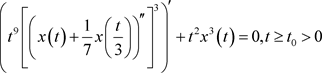 (14)
(14)
其中,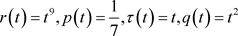 ,取
,取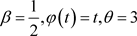 ,
,
且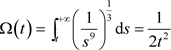 ,则
,则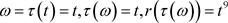 ,
,
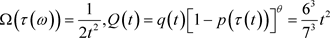
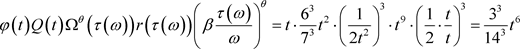
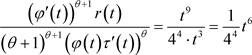
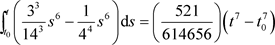
令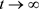 ,
,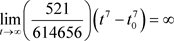 ,且
,且
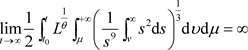
显然式(14)满足定理2.1,故方程(14)是振动的或者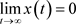 。而方程(14)的结论无法由文献 [9] 的相关结论得到。
。而方程(14)的结论无法由文献 [9] 的相关结论得到。
基金项目
广东省化工学院理学院科研扶持基金重点项目(KY2018001);广东石油化工学院大学生创新创业培育项目(733442)。
文章引用
李 丹,陈淳智,林靖杰,郑量天. 一类三阶半线性时滞微分方程的振动性
Oscillation of a Class of Third-Order Semilinear Delay Differential Equations[J]. 应用数学进展, 2020, 09(03): 437-443. https://doi.org/10.12677/AAM.2020.93053
参考文献
- 1. 杨甲山, 张晓建. 时间模上三阶非线性时滞动态方程的振动性[J]. 浙江大学学报(理学版), 2014, 41(3): 275-281.
- 2. 惠远先, 王俊杰. 三阶中立型半线性时滞微分方程的振动性[J]. 井冈山大学学报, 2017, 38(1): 8-13.
- 3. 俞元洪. 三阶非线性中立型泛函微分方程的振动性[J]. 滨州学院学报数学, 2010, 26(6): 1-6.
- 4. 胡迎春, 白玉真. 一类三阶非线性中立型时滞微分方程的振动性[J]. 曲阜师范大学学报(自然科学版), 2013, 39(2): 60-65.
- 5. 张晓建, 杨甲山. 时间模上二阶非线性动态方程振荡性的新结果[J]. 浙江大学学报(理学版), 2014, 41(5): 499-505.
- 6. 云辉, 俞元洪. 三阶半线性时滞微分方程的振动定理[J]. 系统科学与数学, 2014, 34(2): 231-237.
- 7. 杨甲山, 张晓建. 时间模上一类二阶非线性动态方程振荡性的新结果[J]. 华东师范大学学报(自然科学版), 2017, 5(3): 54-63.
- 8. 林文贤. 三阶半线性中立型阻尼泛函微分方程的振动性[J]. 华东师范大学学报: 自然科学版, 2017(3): 48-53.
- 9. 李全娣, 杨菊, 黎小贤, 林全文. 一类三阶中立型半线性时滞微分方程的振动准[J]. 理论数学, 2017, 7(4): 356-362.
- 10. Erbe, L. (1973) Oscillation Criteria for Second Order Nonlinear Delay Equations. Canadian Mathematical Bulletin, 16, 49-56. https://doi.org/10.4153/CMB-1973-011-1
- 11. 郑量天, 李全娣, 林靖杰, 李晓丹. 一类三阶半线性时滞微分方程振动准则[J]. 理论数学, 2019, 9(9): 1075-1081.
- 12. 林靖杰, 曾伟宏, 李丹. 三阶半线性中立型时滞微分方程得振动性[J]. 广东石油化工学院学报, 2020, 30(1): 48-53.
- 13. 伍思敏, 林靖杰, 李全娣, 等. 一类三阶半线性中立型时滞微分方程的振动性[J]. 应用数学进展, 2019, 8(3): 473-480.