Advances in Applied Mathematics
Vol.
12
No.
03
(
2023
), Article ID:
62577
,
13
pages
10.12677/AAM.2023.123104
CEV模型和违约风险下具有稀疏相依风险的 鲁棒最优再保险和投资策略
张雨萌,马世霞,张欣茹
河北工业大学理学院,天津
收稿日期:2023年2月13日;录用日期:2023年3月9日;发布日期:2023年3月16日

摘要
本文研究了一个具有稀疏相依风险的模糊厌恶保险公司(AAI)的最优再保险和投资问题。AAI通过购买比例再保险来控制保险风险,再保险保费遵循广义期望值–方差原则,并将其财富投资于一个储蓄账户、股票和可违约债券组成的金融市场,其中股票价格过程服从常方差弹性(CEV)模型。以终端财富的期望指数效用最大为目标,利用随机控制方法分别建立了违约后和违约前的鲁棒Hamilton-Jacobi-Bellman (HJB)方程,并分别推导出鲁棒最优再保险和投资策略和相应的值函数。最后,用数值例子分析了模型参数对鲁棒最优策略的影响并给出相应的经济解释。
关键词
鲁棒最优控制,稀疏相依,CEV模型,违约风险

Robust Optimal Investment and Reinsurance Strategies with Thinning Dependent Risks under CEV Model and Default Risk
Yumeng Zhang, Shixia Ma, Xinru Zhang
School of Science, Hebei University of Technology, Tianjin
Received: Feb. 13th, 2023; accepted: Mar. 9th, 2023; published: Mar. 16th, 2023

ABSTRACT
This paper investigates the optimal reinsurance and investment problem with thinning dependent risks for an ambiguity-averse insurer (AAI). It is assumed that AAI manages insurance risk by purchasing proportional reinsurance, in which the reinsurance premium is calculated by the generalized mean-variance premium principle, and its wealth is invested in a financial market consisting of a saving account, a defaultable bond and a stock whose price process obeys the constant elasticity of variance (CEV) model. The AAI aims to maximize the expected exponential utility of terminal wealth. The HJB equation corresponding to the robust optimal problem is established by using stochastic control method, and the robust optimal strategy and value function are obtained for the pre-default and post-default case respectively. Finally, numerical examples are presented to illustrate the effects of parameters on the robust optimal strategies and the corresponding economic explanations are given.
Keywords:Robust Optimal Control, Thinning Dependent, CEV Model, Default Risk

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在复杂的保险业和市场环境下,保险公司面临的风险主要来源于保险业务中产生的索赔风险和金融市场中存在的投资风险,合理地进行再保险和投资是应对风险的常用手段。许多学者致力于最优再保险和投资问题的研究,其主要运用三种优化准则:破产概率最小化 [1] 、终端财富的期望效用最大化 [2] 以及均值–方差准则 [3] 。
目前已有大量文献研究最优再保险和投资问题,除了考虑经典的保险风险过程,具有相关保险业务类别的风险过程也引起了学者们的关注。Liang等 [4] 和Yuen等 [5] 用具有共同冲击的相依风险模型来描述保险风险过程,Sun等 [6] 和Zhang等 [7] 在Yuen等 [5] 的基础上考虑了一个具有两个(或以上)相依保险业务的风险模型。除了上述相依风险模型,Wang等 [8] 提出了稀疏相依风险模型,即:一个类别中的索赔可能以一定概率p引发其他类别的索赔,其他类别的累积索赔过程是一个p稀疏相依过程。该模型在现实生活中广泛存在,如一场严重的交通事故不仅会造成财产损失,还可能造成医疗费用等,Han等 [9] 和Zhang等 [10] 即在该模型下研究了再保险和投资的优化问题。另外,传统文献中 [3] [4] [5] 总是假设决策者可以准确地知道真实的概率测度,而实际上决策者对模型常有怀疑,模型参数难以精确估计。因此,考虑模糊性是十分有必要的,Sun等 [11] 和Zheng等 [12] 即在优化问题中加入了模糊性的考虑。除此之外,金融市场的复杂性也极大地影响着再保险和投资策略的制定。一方面,金融市场中风险资产的波动率是随机的,于是用随机波动率模型来描述更贴合现实,常见的有Heston模型如Zhang等 [10] 和CEV模型如Wang等 [13] ,但是目前将模糊性和CEV模型结合来研究此类问题的文献很少。另一方面,违约债券的高回报率吸引着众多保险公司,故考虑带违约债券的金融市场更贴近实际,如Wang等 [14] 。
于是,受上述研究的启发,本文在稀疏相依风险模型描述的保险风险过程下研究保险公司的最优再保险和投资策略。与Zhang等 [10] 不同的是,假设保险公司是模糊厌恶的,购买比例再保险且遵循广义期望值–方差保费原则,风险资产的波动性用CEV模型描述并考虑了带违约债券的金融市场。在此基础上,利用动态规划方法,通过采用新颖的值函数形式推导了违约后和违约前的鲁棒最优解,并通过数值分析给出经济解释和一些建议。
2. 模型构建
假设
是一个给定的完备全概率空间,并假设下面介绍的所有过程都是此空间中定义良好的和适应的过程。
2.1. 余额过程
假设风险模型是由两个相依类别的保险业务组成的,保险公司的余额过程为:
(1)
式中,
是初始余额,保费率c遵循期望值原则,即
,
是安全载荷。
是第一类索赔的大小并假设
是独立同分布的正随机变量且分布函数为
,有限的一阶矩
和二阶矩
,
是第二类索赔的大小且
,
。
索赔计数过程
表示在
内索赔发生的数目,假定它是一个强度为
的泊松过程,
是
的p稀疏相依过程具有强度
,即第一类保险业务的每一项索赔可能会也不可能不会引起第二类保险业务的索赔,如果发生索赔,则第一类的保险业务以概率p导致第二类保险业务的索赔发生。第一类的每次索赔是否引起第二类保险业务的索赔是相互独立的,且
,
和
是相互独立的。
保险公司为了避免大额索赔而购买比例再保险。对于每个
,比例再保险水平用风险暴露值
表示,分别对应索赔
。加入再保险策略
后,保险公司的余额过程为:
(2)
这里采用广义期望值-方差保费原则来计算再保险保费,即:
(3)
注1 当
时,再保险保费退化到期望值保费原则。当
时,退化到方差保费原则。
根据Zhang等 [10] 和Grandell [15] 将索赔过程作近似,即:
则余额过程(2)可近似为扩散过程:
(4)
式中,
和
是标准布朗运动具有相关系数
。
2.2. 金融市场
保险公司投资于由储蓄账户,股票和违约债券组成的金融市场。储蓄账户的价格过程为:
(5)
式中,
是无风险利率。假设股票
的价格过程服从CEV模型,即:
(6)
式中,
是期望瞬时回报率,
是一个正的常数,
是弹性参数,
是瞬时波动率。这里假设
,
且
与
,
相互独立。
注2 当
时,CEV模型退化到几何布朗运动(GBM)模型。
下面介绍违约债券。令
是P测度下强度为
的泊松过程的第一个跳跃时间,它表示违约时间。定义违约示性过程
,
即有跳跃发生,否则其取值为0,故
和
分别表示违约前和违约后的情况。令
和
分别表示违约过程
的信息流以及
和
的扩大信息流,那么
是使得
为停时的最小信息流,则过程
是在P测度下的G-鞅。令
为违约到期日,
表示违约风险溢价,
是违约发生时债券的损失率。根据Girsanov's定理 [14] ,存在风险中性测度
(等价于测度P)下,在测度
违约到达强度为
。用
表示违约债券的价格,
为风险中性测度
下的信用利差,故违约债券的价格过程为:
(7)
用
表示保险公司在t时刻分别投资在股票、违约债券的金额。在策略
下,保险公司的财富过程为:
(8)
3. 指数效用下的鲁棒最优控制
假设保险公司的目标是在有限时间T内最大化终端财富的期望指数效用,即
(9)
其中,
是在概率测度P下的期望,
是绝对风险厌恶系数,
是所有可行策略集。此模型中保险公司是模糊中性的,而实际多数保险公司是模糊厌恶的,下面加入模糊性的考虑。
假设有一个参考模型来描述保险和金融风险,并且用概率测度P来描述。由于参数的不确定性,保险公司对参考模型持怀疑态度,于是考虑一些替代模型来寻找最优策略。假设替代模型和参考模型之间的差异由概率测度的变化来描述的,定义一类绝对连续的等价于P的概率测度作为可替代测度
。根据Girsanov’s定理,对于
,存在一个过程
使得
,其中
是一个P-鞅。
注3过程
满足下面条件:
i)
是
-可测的对每一个
,
ii)对于a.s.
,
,
iii)
,其中
。
用
表示所有过程
的集合。由Girsanov’s定理,在替代测度Q下,
和
变换为标准布朗运动
和
,泊松过程的强度变为
,并且
定义1对任意
,策略
称为可行的,如果:
1)
是
-可测的;
2)
,
和
;
3)
是随机微分方程(8)的唯一强解。
令
表示所有可行策略集。保险公司在概率测度Q下的财富过程为:
(10)
保险公司认为参考模型P是真实模型的近似且可替代模型不应偏离P太大,故用可替代模型和参考模型之间的距离来惩罚任何偏离。假设保险公司的目标是寻求鲁棒最优再保险和投资组合以保护自己不面对最坏情况,根据Maenhout [16] 构建一个鲁棒最优问题来修正(9):
(11)
式中,
且期望
是在测度Q下给定初始值
计算的,较参考测度产生的偏差会受到期望中第二项的惩罚,此惩罚项取决于由扩散风险和跳跃风险产生的相对熵。参考Wang等 [14] 的附录A,相对熵从t到
的增量为:
(12)
下面利用动态规划方法解决优化问题(11)。鲁棒最优问题的HJB方程为:
(13)
具有边界条件
,变分算子
如下:
为了易于处理,参考Maenhout [16] 提出的观点,
状态相依即
,
是模糊厌恶系数(
表示模糊中立)。
4. 鲁棒最优问题的解
对违约后和违约前的情况,分别推导了HJB方程(13)的显式解和相应的值函数。
4.1. 违约后的情况
投资在违约债券的金额为0,
。将
代入(13)得:
(14)
根据(14)的结构和边界条件,推测值函数为如下形式:
(15)
式中,
是满足
的函数且使得(15)是(13)的解。
将
和其各偏导代入 (14) ,并对
利用一阶最优条件得到:
(16)
再将(16)代回HJB方程,根据一阶最优条件得到:
(17)
引理1记函数
为:
(18)
是关于
的凸函数,其存在唯一的最优解
。
证明:函数关于
的一阶偏导数和二阶偏导数如下:
Hessian矩阵为:
,故
根据前面参数设置可知此值前两项均大于0,最后一项中的行列式根据柯西不等式可得到大于0,故
,Hessian矩阵正定,
是关于
的凸函数。再利用初等不动点定理可得
和
的唯一。
将(17)代回HJB方程,得到值函数
满足如下的随机微分方程:
(19)
(20)
结合边界条件
得到:
(21)
(22)
4.2. 违约前的情况
对于违约前,
,HJB方程转化为:
(23)
具有边界条件
。猜测值函数有如下形式:
(24)
式中,
满足
。
将
和其各偏导代入(23),并对
利用一阶最优条件得到:
(25)
将对(23)代回HJB方程,对
求一阶偏导得到鲁棒最优策略:
(26)
再将(25)代回HJB方程并分离变量可得:
(27)
(28)
求解得到
,那么
。
由于
,为得到
,设
,结合边界条件
,有:
(29)
将
和
结合起来,得到非线性方程:
(30)
引理2 设
定义为
,则存在一个
使
。
证明:证明类似于Zhang等 [2] 的引理1,这里省略。
最后,综合违约后和违约前的情况可得到鲁棒最优策略以及值函数的表达式。
定理1 在模糊厌恶情况下的鲁棒最优再保险–投资策略以及值函数为:
式中,
,
和
见(21)、(22)、(29)。
定理2 如果存在
和一个控制策略
满足HJB方程 (13) ,则
是最优策略并且
是相应的值函数。
证明:证明类似于Sun等 [11] ,这里不再赘述。
5. 数值分析
本节进行数值分析说明部分参数对鲁棒最优再保险和投资策略的影响。参数设置如下:
首先分析鲁棒最优再保险策略。如图1所示
和
均随着时间t的增加而增加,说明随着时间的推移,保险公司将从保险业务和投资中获得大量财富,提升承担保险风险的能力,从而提高风险保留水平
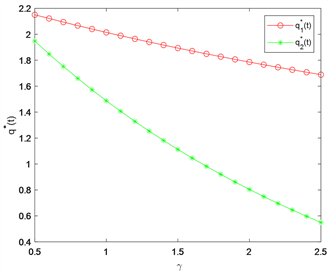
即降低再保险比例。另外分析了风险规避系数
的影响,从图2可以看出:随着
的增大,保险公司会降低风险保留水平
,相对保守地购买再保险来减少自身的潜在索赔。
最后分析鲁棒最优投资策略。
表示保险公司对扩散风险的模糊厌恶程度,如图3所示,
越大,保险公司对参考模型的可信度就越低,因此投资于股票的财富数量就会越少。图4反映了弹性参数
对
的影响,在
时,最优策略
会随着
的增加而减少,而当
时,投资于股票的最优策略
会增加。图5说明了违约债券
与不同参数之间的关系。随着损失率
的增加,保险公司投资于违约债券的资金有所减少,这与损失率较高会导致债券回收值降低的事实是一致的。随着信用利差
的增长,保险公司会更多地投资违约债券获取高额利润。
保险公司总是希望在风险尽可能低的情况下获得更多的收益,风险厌恶程度影响着其决策,上述分析恰恰给出了模糊厌恶型保险公司在不同参数变化下的正确决策倾向,有利于其在复杂的金融市场条件下开展保险业务和资产管理。
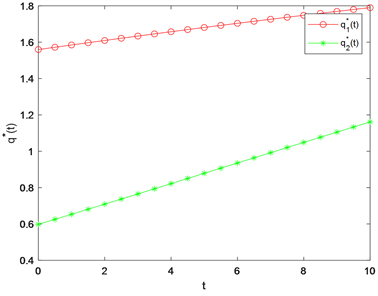
Figure 1. The situation of
with time
图1.
随时间t的变化情况
图2. 参数
对
的影响
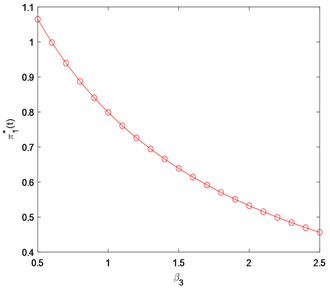
Figure 3. The effect of
on
图3. 参数
对
的影响
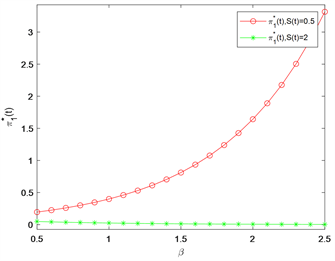
Figure 4. The effect of
on
图4. 参数
对
的影响
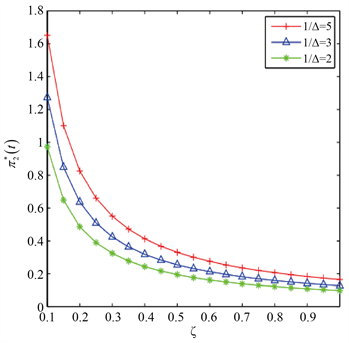
Figure 5. The effects of parameters
and
on the strategy
图5. 参数
和
对违约债券投资策略
的影响
文章引用
张雨萌,马世霞,张欣茹. CEV模型和违约风险下具有稀疏相依风险的鲁棒最优再保险和投资策略
Robust Optimal Investment and Reinsurance Strategies with Thinning Dependent Risks under CEV Model and Default Risk[J]. 应用数学进展, 2023, 12(03): 1022-1034. https://doi.org/10.12677/AAM.2023.123104
参考文献
- 1. Liang, X.Q., Liang, Z.B. and Young, V.R. (2020) Optimal Reinsurance under the Mean-Variance Premium Principle to Minimize the Probability of Ruin. Insurance Mathematics and Economics, 92, 128-146.
https://doi.org/10.1016/j.insmatheco.2020.03.008
- 2. Zhang, Q. and Chen, P. (2019) Robust Optimal Proportional Reinsurance and Investment Strategy for an Insurer with Defaultable Risks and Jumps. Computational and Applied Mathematics, 356, 46-66.
https://doi.org/10.1016/j.cam.2019.01.034
- 3. Zhao, H., Shen, Y. and Zeng, Y. (2016) Time-Consistent Invest-ment-Reinsurance Strategy for Mean-Variance Insurers with a Defaultable Security. Mathematical Analysis and Applica-tions, 437, 1036-1057.
https://doi.org/10.1016/j.jmaa.2016.01.035
- 4. Liang, Z.B. and Yuen, K.C. (2016) Optimal Dynamic Reinsurance with Dependent Risks: Variance Premium Principle. Scandinavian Actuarial, 1, 18-36. https://doi.org/10.1080/03461238.2014.892899
- 5. Yuen, K.C., Liang, Z.B. and Zhou, M. (2015) Optimal Pro-portional Reinsurance with Common Shock Dependence. Insurance Mathematics and Economics, 64, 1-13. https://doi.org/10.1016/j.insmatheco.2015.04.009
- 6. Sun, J.Y., Yao, H.X. and Kang, Z.L. (2019) Robust Optimal Reinsurance-Investment Strategies for an Insurer with Multiple Dependent Risks. Insurance Mathematics and Econom-ics, 89, 157-170.
https://doi.org/10.1016/j.insmatheco.2019.09.006
- 7. Zhang, Y. and Zhao, P.B. (2019) Robust Optimal Ex-cess-of-Loss Reinsurance and Investment Problem with Delay and Dependent Risks. Discrete Dynamics in Nature and Society, 21, Article ID: 6805351.
https://doi.org/10.1155/2019/6805351
- 8. Wang, G.J. and Yuen, K.C. (2005) On a Correlated Aggregate Claims Model with Thinning-Dependence Structure. Insurance Mathematics and Economics, 36, 456-468. https://doi.org/10.1016/j.insmatheco.2005.04.004
- 9. Han, X., Liang, Z.B. and Yuen, K.C. (2018) Optimal Pro-portional Reinsurance to Minimize the Probability of Drawdown under Thinning-Dependence Structure. Scandinavian Actuarial, 10, 863-889.
https://doi.org/10.1080/03461238.2018.1469098
- 10. Zhang, Y., Zhao, P.B. and Kou, B.Y. (2021) Optimal Ex-cess-of-Loss Reinsurance and Investment Problem with Thinning Dependent Risks under Heston Model. Computational and Applied Mathematics, 382, Article ID: 113082.
https://doi.org/10.1016/j.cam.2020.113082
- 11. Sun, Z.Y., Zheng, X.X. and Zhang, X. (2017) Robust Optimal In-vestment and Reinsurance of an Insurer under Variance Premium Principle and Default Risk. Mathematical Analysis and Applications, 446, 1666-1686.
https://doi.org/10.1016/j.jmaa.2016.09.053
- 12. Zheng, X.X., Zhou, J.M. and Sun, Z.Y. (2016) Robust Optimal Portfolio and Proportional Reinsurance for an Insurer under a CEV Model. Insurance Mathematics and Economics, 67, 77-87.
https://doi.org/10.1016/j.insmatheco.2015.12.008
- 13. Wang, S.X., Rong, X.M. and Zhao, H. (2019) Optimal Time-Consistent Reinsurance-Investment Strategy with Delay for an Insurance under a Defaultable Market. Mathematical Analysis and Applications, 474, 1267-1288.
https://doi.org/10.1016/j.jmaa.2019.02.016
- 14. Wang, N., Zhang, N., Jin, Z., et al. (2019) Robust Non-Zero-Sum Investment and Reinsurance Game with Default Risk. Insurance Mathematics and Economics, 84, 115-132. https://doi.org/10.1016/j.insmatheco.2018.09.009
- 15. Grandell, J. (1991) Aspects of Risk Theory. Spring-er-Verlag, New York. https://doi.org/10.1007/978-1-4613-9058-9
- 16. Maenhout, P.J. (2004) Robust Portfolio Rules and Asset Pricing. Review of Financial Studies, 17, 951-983.
https://doi.org/10.1093/rfs/hhh003