异方差模型平均的稀疏化赋权 Sparsified Weighting of Heteroscedasticity Model Averaging

doi:10.12677/AAM.2023.128368

Advances in Applied Mathematics
Vol. 12 No. 08 ( 2023 ), Article ID: 71163 , 9 pages
10.12677/AAM.2023.128368

异方差模型平均的稀疏化赋权

刘芳琳，邹晨晨^*

●How to Cite this Article

青岛大学数学与统计学院，山东青岛

收稿日期：2023年7月26日；录用日期：2023年8月18日；发布日期：2023年8月24日

摘要

本文针对具有异方差误差的线性回归模型，在一种可行的Mallows’Cp准则提出的异方差稳健Cp(HRCp)模型平均方法基础上，考虑HRCp模型平均权重的稀疏性，使用坐标下降算法对异方差模型平均进行稀疏化赋权。数值模拟表明，用坐标下降算法改进的HRCp模型平均方法在候选模型较少或者中等、样本量不大时，相对于其他的模型平均方法有较小的损失风险，能更好的拟合模型。

关键词

模型平均，异方差，稀疏化赋权，坐标下降算法

Sparsified Weighting of Heteroscedasticity Model Averaging

Fanglin Liu, Chenchen Zou^*

School of Mathematics and Statistics, Qingdao University, Qingdao Shandong

Received: Jul. 26^th, 2023; accepted: Aug. 18^th, 2023; published: Aug. 24^th, 2023

ABSTRACT

Based on the averaging method of heteroscedasticity robust Cp (HRCp) model proposed by a feasible Mallows’ Cp criterion, this paper considers the sparsity of the average weight of the HRCp model, and uses the coordinate-wise descent algorithm to sparse the average weight of the heteroscedasticity model. Numerical simulation shows that the improved HRCp model averaging method with coordinate-wise descent algorithm has less loss risk compared with other model averaging methods when the candidate models are few or medium and the sample size is not large, and can fit the model better.

Keywords:Model Averaging, Heteroscedasticity, Sparsified Weighting, Coordinate-Wise Descent Algorithm

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

模型平均是当代统计学和计量经济学界备受瞩目的国际性话题，它是用一定的权重对来自不同模型的估计或预测进行有效地组合，从而获得较为稳健的估计，在经济、金融、生物、医学等领域有广泛的应用前景。模型平均没有忽视模型选择过程产生的不确定性，估计一般比模型选择更加稳健，可用减少有用信息的遗失。新近提出的模型平均方法多直接以降低估计或预测的风险作为目标，因而目标更加明确，比如渐近最优的模型平均方法。总之，随着计算机技术的提升，模型平均作为一种更加复杂的数据挖掘方法正在越来越多被使用。

对于异方差模型，Andrews (1991) [1] 提出了异方差模型的模型选择方法，但没有提供该准则的可行形式。Hansen和Racine (2012) [2] 提出了Jackknife model averaging (JMA)，其使用交叉验证标准来选择权重。Liu和Ryo Okui (2013) [3] 针对具有异方差误差的线性回归模型，提出了异方差稳健Cp(HRCp)模型平均方法。Liu (2015) [4] 在局部渐近框架中提出了模型平均估计量，并基于渐近均方误差表达式推导了插入式平均估计量的渐近分布。Ando和Li (2014) [5] 最近研究了高维回归的模型平均，其主要特点是模型权重可以在0和1之间自由变化，而不受求和为1的标准限制，并建立了一个定理，用留一交叉验证方法证明了权重选择的渐近最优性。Charkhi，Claeskens和Hansen (2016) [6] 考虑了一般情况下由极大似然估计得到的估计量，用其插入估计量替换未知的位置参数，并建议选择最小化MSE估计值的权重。Zhang等(2016) [7] 研究了广义线性模型和广义线性混合效应模型的最优模型平均，提出了基于Kullback-Leibler (KL距离)损失惩罚项的权重选择标准。Zhu等(2018) [8] 针对半参数变系数部分线性模型，发展了一个分配模型权重的Mallows型准则，并证明了其渐近最优性。Zhao等(2020) [9] 考虑了一个具有乘性异方差的回归模型，通过结合模型均值和方差函数中未知参数的最大似然估计进行模型平均，其权重选择标准是基于模型平均估计值平方预测风险的插入式估计值的最小化。Zhang和Liu (2022) [10] 考虑准似然框架中的模型平均预测，通过最小化K折交叉验证来选择模型平均的最优权重。本文针对异方差模型平均问题，选取了常用的HRCp异方差模型平均方法，探究其目标函数与Lasso的关系，并对其稀疏解展开具体研究。

Lasso (Least absolute shrinkage and selection operator)方法用模型系数的绝对值函数作为惩罚来压缩模型系数，使绝对值较小的系数自动压缩为，从而同时实现显著性变量的选择和对应参数的估计。相较于子集选择和岭回归等传统的OLS估计改进方法，Lasso改进普通最小二乘(Ordinary Least Square, OLS)估计的优势更多一些。近些年来，Lasso惩罚适用于多种模型，新开发的计算算法允许将这些模型应用于大型数据集，利用稀疏性获得统计信息并计算收益，故有关Lasso的工作正在包括统计、工程、数学和计算机科学等许多领域如火如荼地展开。

本文将在Liu和Ryo Okui (2012) [3] 针对具有异方差误差的线性回归模型，采用了一种可行的Mallows’Cp准则提出的异方差稳健Cp (HRCp)模型平均方法基础上，考虑HRCp模型平均权重的稀疏性，使用坐标下降算法(Coordinate-wiseDescent Algorithm，简称CD算法)对异方差模型平均进行稀疏化赋权，这也是本文的主要创新点。

2. HRCp-Lasso

考虑n个独立随机样本 ${(x_{i}, y_{i}), i = 1, \dots, n}$ ，其数据产生过程为：

$y_{i} = \sum_{j = 1}^{\infty} θ_{j} x_{i j} + e_{i} = μ_{i} + e_{i}, i = 1, \dots, n$ (1)

其中， $y_{i}$ 是响应变量， $x_{i} = (x_{i 1}, x_{i 2}, \dots)$ 是解释变量，其具有可数无限个元素， $ε_{i}$ 是随机误差项。令 $Y = {(y_{1}, \dots, y_{n})}^{'}$ ， $X = {({x^{'}}_{i}, \dots, {x^{'}}_{n})}^{'}$ ， $μ = {(μ_{1}, \dots, μ_{n})}^{'}$ ， $ε = {(e_{1}, \dots, e_{n})}^{'}$ 。假设 $E (e_{i} | x_{i}) = 0$ ，故Y的条件期望为 $E (Y | X) = μ$ 。假设 $Var (e_{i} | x_{i}) = σ_{i}^{2}$ ，即 $e_{i}$ 的条件方差与 $x_{i}$ 有关，此时随机误差项的方差是异方差。

考虑总共M个近似模型，其中第m个近似模型为：

$y_{i} = \sum_{j = 1}^{k_{m}} θ_{j (m)} x_{i j}_{(m)} + e_{i} = μ_{i} + e_{i}, i = 1, \dots, n$ (2)

即，使用了 $k_{m}$ 个 $x_{i j}$ 作为解释变量，用矩阵可表示为：

$Y = X_{(m)} Θ_{(m)} + b_{(m)} + e, m = 1, \dots, M$ (3)

其中， $X_{(m)}$ 是一个 $n \times k_{m}$ 的矩阵，其第 $(i, j)$ 个元素为 $x_{i j}_{(m)}$ ，它是由X的任意 $k_{m}$ 列组成的， $Θ_{(m)}$ 为相应的系数向量。此时，第m个模型 $μ$ 的最小二乘估计为：

${\hat{μ}}_{m} = X_{(m)} Θ_{(m)} = X_{(m)} {({X^{'}}_{(m)} X_{(m)})}^{- 1} {X^{'}}_{(m)} y = P_{m} y$ (4)

其中， $P_{m} = X_{(m)} {({X^{'}}_{(m)} X_{(m)})}^{- 1} {X^{'}}_{(m)}$ 为投影矩阵。

记模型的权重向量 $w = {(w_{1}, \dots, w_{M})}^{'}$ ，并限制在如下权重集合中：

$H_{M} = {w \in {[0, 1]}^{M} : \sum_{m = 1}^{M} w_{m} = 1}$ (5)

则 $μ$ 的模型平均估计为：

$\hat{μ} (w) = \sum_{m = 1}^{M} w_{m} {\hat{μ}}_{m} = \sum_{m = 1}^{M} w_{m} P_{m} y = P (w) y$ (6)

根据Liu和Ryo Okui (2012) [10] 提出的异方差稳健Cp (HRCp)模型平均方法，HRCp选择权重w是根据极小化下式得到：

$HRCp (w) = {‖ Y - \sum_{m = 1}^{M} w_{m} {\hat{μ}}_{m} ‖}^{2} + 2 \sum_{m = 1}^{M} w_{m} (\sum_{i = 1}^{n} {\hat{e}}_{i}^{2} P_{i i}^{(m)})$ (7)

$s .t . w \in H_{M} = {w \in {[0, 1]}^{M} : \sum_{m = 1}^{M} w_{m} = 1}$

其中 $\sum_{m = 1}^{M} w_{m} {\hat{μ}}_{m}$ 是对 $μ$ 的估计， $x_{i (m)}$ 表示 $X_{(m)}$ 的第i列， ${\hat{e}}_{i}$ 表示残差。令 $Z = {({\hat{μ}}_{1}, \dots, {\hat{μ}}_{M})}_{n \times M}$ ，其是一个 $n \times M$ 的矩阵，它的列是来自M个候选模型的拟合响应向量， $P_{i i}^{(m)}$ 是第m个模型的帽子矩阵的第i个对角线元素。则HRCp优化问题可以写成最小化下列式子：

$HRCp (w) = \frac{1}{2} {‖ y - Z w ‖}_{2}^{2} + \sum_{m = 1}^{M} | w_{m} | \sum_{i = 1}^{n} {\hat{e}}_{i}^{2} p_{i i}^{(m)}$ (8)

$s .t . w \in H_{M} = {w \in {[0, 1]}^{M} : \sum_{m = 1}^{M} w_{m} = 1}$

而对于经典的线性模型 $y_{n \times 1} = Z_{n \times M} w_{M \times 1} + ε_{n \times 1}$ ，我们可以利用Lasso方法找到一个w使得下式达到最小：

$\tilde{HRCp} (w) = \frac{1}{2} {‖ y - Z w ‖}_{2}^{2} + \sum_{m = 1}^{M} λ_{m} | w_{m} |$ (9)

$s .t . w \in H_{M} = {w \in {[0, 1]}^{M} : \sum_{m = 1}^{M} w_{m} = 1}$

其中 $λ_{i} (i = 1, \dots, M)$ 是不同w的惩罚向量。

对比上述两个式子，可以看出HRCp的权重估计问题与Lasso之间的对应关系，其中回归系数为权重(w)，惩罚权重 $λ_{m} = {\hat{e}}^{2} p^{(m)} = \sum_{i = 1}^{n} {\hat{e}}_{i}^{2} p_{i i}^{(m)}$ 。因此，我们可以将HRCp看作是带有约束条件的Lasso问题，并可以使用Lasso问题的相关算法来求解模型平均问题中的权重。

3. 坐标下降算法

许多经典模型平均方法对于权重的求解采用的是二次规划算法，例如MMA、JMA等。坐标下降法算法(Coordinate-wiseDescent Algorithm，简称CD算法)已经在处理高维数据的稀疏解问题上得到了广泛而成功的应用。如上文所述，我们可以把异方差模型平均问题看作一个Lasso问题，故我们可以利用CD算法来优化求解过程，从而更好地对异方差模型平均进行稀疏化赋权。

我们参考Feng等(2020) [3] 对于MMA的处理，将关于w的等式限制条件 $\sum_{m = 1}^{M} w_{m} = 1$ 转换为在目标函数中加上 $\frac{γ}{2} {(1_{M}^{T} w - 1)}^{2}$ ，其中 $γ$ 是一个足够大的数。故我们可以将HRCp等价转换：

$min {f_{n} (w) = \frac{1}{2} {‖ y - Z w ‖}_{2}^{2} + {\hat{e}}^{2} \sum_{m = 1}^{M} | w_{m} | p^{(m)} + \frac{γ}{2} {(1_{M}^{T} w - 1)}^{2}}$ (10)

$s .t . w_{m} \geq 0, m = 1, 2, \dots, M$

其次梯度函数为：

$\frac{\partial f_{n} (w)}{\partial w_{m}} = - {\hat{μ}}^{'}_{m} (y - Z w) + {\hat{e}}^{2} p^{(m)} + γ ({1^{'}}_{m} w - 1)$ (11)

故我们可以给定一个初始权重 $w^{(0)}$ ，令次梯度函数 $\frac{\partial f_{n} (w)}{\partial w_{m}} = 0$ ，得到 $w_{m}$ 的权重更新公式：

${\hat{w}}_{m} = \frac{{[{\hat{μ}}^{'}_{m} (y - Z_{- m} w_{- m}) - γ ({1^{'}}_{m} w - 1) - {\hat{e}}^{2} p^{(m)}]}^{+}}{γ + {\hat{μ}}^{'}_{m} {\hat{μ}}_{m}}$ (12)

其中， $Z_{- m}$ 表示Z去掉第m列， $w_{- m}$ 表示没有第m个元素， $m = 1, 2, \dots, M$ 。坐标下降法具体算法见表1：

Table 1. Coordinate-wise descent alggorithm for HRCp

表1. HRCp的坐标下降算法

4. 数值模拟

我们将考虑两种情形：一种是嵌套模型；另一种是非嵌套模型。通过比较分析在不同的样本量和变量数的情况下，SAIC、SBIC、MMA、JMA、HRCp以及HRCp_CD模型平均方法的估计风险，从而对本文改进的异模型平均方法进行评价。

估计风险由二次损失函数的均值衡量，即，

$R i s k = \frac{1}{D} \sum_{d = 1}^{D} {‖ \hat{μ} {(ω)}_{(d)} - μ_{(d)} ‖}^{2}$ (13)

其中d表示第d次产生数据，在模型中，我们令 $D = 1000$ 。为了便于比较，我们将每个方法的估计风险除以HRCp_CD的估计风险。

4.1. 嵌套模型

根据以下数据生成过程得到有限随机数据，即在 $k = 1000$ 时截断：

$y_{i} = \sum_{j = 1}^{k} θ_{j} x_{j i} + e_{i}, i = 1, \dots, n$ (14)

其中， $x_{1 i} = 1$ ， $(x_{2 i}, \dots, x_{k i}) ~ N_{k - 1} (0, 1)$ ， $e_{i} ~ N (0, σ_{i}^{2})$ ， $σ_{i}^{2} = x_{2 i}^{4} + 0.01$ ，故我们保证了方差是严格正定的。令参数 $θ_{j} = c j^{- 1}$ ， $R^{2} = (var (y_{i}) - var (e_{i})) / var (y_{i}) = (\sum_{j = 1}^{\infty} θ_{j}^{2}) / (\sum_{j = 1}^{\infty} θ_{j}^{2} + 3.01)$ ，我们可以通过改变c的值来控制R²，使之从0.1增加到0.9。令HRCp的坐标下降算法收敛阈值 $ε = 1 \times 10^{- 7}$ ，最大迭代步长 $K = 1 \times 10^{5}$ ，惩罚项参数 $γ = 100$ 。

嵌套模型，即第 $k + 1$ 个模型中一定包含第k个模型中的所有解释变量。假设解释变量的个数为p，则候选模型的数量 $M = p$ ，第m个候选模型包括前m个解释变量。我们分别令 $n = 50$ ， $M = 5$ ； $n = 100$ ， $M = 5$ ； $n = 100$ ， $M = 10$ ； $n = 400$ ， $M = 15$ ，模拟结果见图1：

根据图1可知，在嵌套模型设置情况下，SAIC和SBIC总体来说表现不好，相对于其他模型平均方法MMA、JMA、HRCp以及HRCp_CD来说，有较大的损失风险。MMA在误差项异方差的设置下仅优于SAIC和SBIC，远不如JMA、HRCp和HRCp_CD。这基本符合我们现有的研究认知，因为JMA、HRCp和HRCp_CD都是针对误差项异方差提出的模型平均方法，而MMA是针对误差项同方差提出的，故在

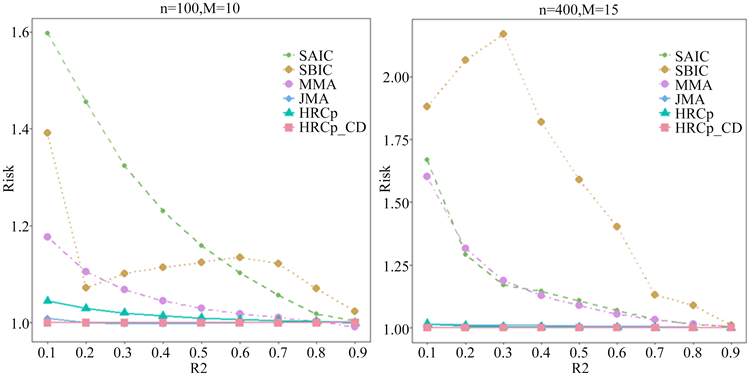
Figure 1. Comparison of various model-averaging methods in the nested setup

图1. 嵌套模型各模型平均方s法的比较

处理异方差模型平均问题上效果比不上针对误差项异方差提出的模型平均方法。当 $R^{2}$ 较小时，JMA相对于HRCp来说有优势。从整体上看，在损失风险方面，HRCp_CD在有限样本中的性能优于其他方法，且在候选模型数量较小或者中等时，优势更加明显。此外我们注意到，当 $R^{2}$ 较小时HRCp_CD与其他模型平均方法的差距要比 $R^{2}$ 较大时要大，但整体来看，本文基于坐标下降算法改进的异方差模型平均方法，即HRCp还是很有优势的。

4.2. 非嵌套模型

非嵌套模型模拟采取线性回归模型，并且回归变量个数有限。数据产生过程，具体如下：

$y_{i} = μ_{i} + e_{i} = \sum_{j = 1}^{9} θ_{j} x_{j i} + e_{i}, i = 1, \dots, n$ (15)

其中， $x_{1 i} = 1$ ， $(x_{2 i}, \dots, x_{k i}) ~ N_{k - 1} (0, 1)$ ， $e_{i} ~ N (0, σ_{i}^{2})$ ， $σ_{i} = (1 + 6 x_{2 i}^{2}) / 11$ ，令 $x_{1 i}, x_{2 i}$ 和 $x_{3 i}$ 为关键核心变量，即在每个候选模型中都必须含有， $x_{4 i}, x_{5 i}, x_{6 i}, x_{7 i}, x_{8 i}$ 和 $x_{9 i}$ 为辅助变量，即可能包含在候选模型中，也可能不包含在候选模型中。给选定参数 $θ = c (\frac{1}{a}, \frac{1}{a}, \frac{1}{a}, \frac{1}{\sqrt{n}} (1, \frac{q - 1}{q}, \dots, \frac{1}{q}))$ ，q是辅助变量的个数。假设每个候选模型中只包含一个辅助变量，则一共有6个候选模型，每个模型中有4个解释变量(3个核心变量和1个辅助变量)。定义为 $R^{2} = \frac{{\tilde{θ}}^{'} \tilde{θ}}{1 + {\tilde{θ}}^{'} \tilde{θ}}$ ，这里 $\tilde{θ} = {(θ_{2}, θ_{3}, \dots, θ_{9})}^{'}$ ，参数c用来控制R²，使R²限定在区间 $[0.1, 0.9]$ 。模拟结果见图2：

根据图2可知，在非嵌套模型设置情况下，由于每个候选模型中的解释变量个数均相同，故SAIC和SBIC相对于HRCp_CD的风险曲线大致重合，总体来说表现不好，比其他模型平均方法MMA、JMA、HRCp以及HRCp_CD有更大的损失风险。MMA相对于JMA、HRCp和HRCp_CD来说表现欠佳，不是处理异方差模型平均问题的首选。当R²和n都较小时，JMA相对于HRCp和HRCp_CD来说有一定的优势，但随着R²和n的增加，JMA没有HRCp_CD有优势。从整体上看，在损失风险方面，HRCp_CD在有限样本中的性能优于其他方法，且在样本数量相对较小时，优势更加明显。

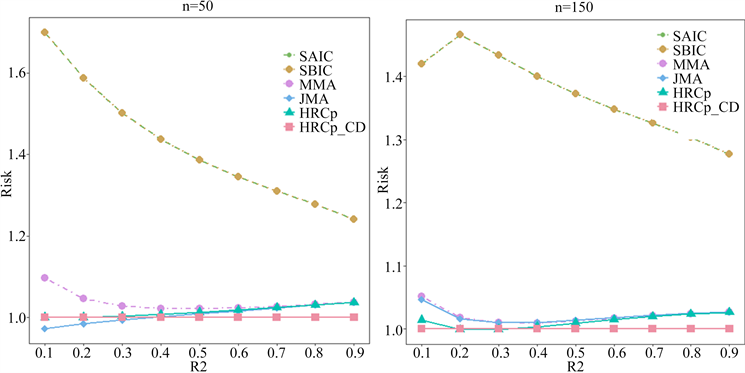
Figure 2. Comparison of various model-averaging methods in the singleton setup

图2. 非嵌套模型各模型平均方法的比较

5. 实例分析

为了比较在数值模拟部分中提到的六种方法的表现，我们根据Zhang [11] 将模型平均方法应用于我国的粮食产量预测，选用了1990~2021年的相关数据，数据来源于中国统计年鉴 (http://www.stats.gov.cn/sj/ndsj/)。我们将数据分为两部分，分别记为训练集和测试集，其中训练集的样本量为 $n_{0} = 10, 20, 30$ ，而测试集的样本量为 $n - n_{0}$ ，其中 $n = 32$ 是整体的样本量。即我们分别用1990~2004年、1990年~2009年、1990年~2014年的粮食产量数据预测2005年~2021年、2010~2021年、2015~2021年的粮食产量，并计算样本均方预测误差(Mean Squared Prediction Error, MSPE)，即

$MSPE = \frac{1}{n - n_{0}} \sum_{i = n_{0} + 1}^{n} {(y_{i} - {\hat{μ}}_{i})}^{2}$ (16)

其中 ${\hat{μ}}_{i}$ 是 $μ_{i}$ 的预测值。我们计算了这六种方法的MSPE，同时为了方便比较，我们将HRCp_CD的MSPE作为分母，从而更直观地看出本文改进的异方差模型平均方法的有效性。结果见表2：

Table 2. MSPE for each model averaging method

表2. 各个模型平均方法的MSPE

根据上述表格，我们可以看出，在不同的训练集样本量下，SAIC、SBIC的预测效果是相对较差的，HRCp_CD的预测效果是最好的，MMA、JMA和HRCp的预测效果比SAIC、SBIC要好，但比HRCp_CD要差。

与此同时，我们总结使用各个模型平均方法求出的权重中零权重的比例，结果见表3：

Table 3. Zero weights proportion for each model averaging method

表3. 各个模型平均方法的零权重的比例

根据表3，我们可以看出，HRCp_CD方法得到的各个候选模型权重中零权重的比例最高，大于MMA、JMA和HRCp得到的零权重的比例，使用SAIC、SBIC方法一般并不能使模型平均某个候选模型的权重为0。故说明本文利用坐标下降算法改进的HRCp模型平均方法能利用较少的候选模型得到较精确的预测，即能有效地对异方差模型平均问题进行稀疏化赋权。

6. 总结

本文主要对异方差线性误差模型的平均估计进行了研究，在现有的异方差模型平均方法HRCp的基础上，将模型平均问题看作一个带约束条件的Lasso问题，并对模型平均的权重进行稀疏化赋权。与此同时，本文还提出了一种新的算法，即利用坐标下降算法来对模型平均的权重进行稀疏化赋权。数值模拟和实例研究表明，用坐标下降算法改进的HRCp模型平均方法在候选模型较少或者中等、样本量不大时，相对于其他的模型平均方法有较小的损失风险，能更好的拟合模型。此外，在实际应用过程中非线性模型应用十分广泛，所以把本文改进的方法推广到非线性模型是非常有意义的，这需要进一步的研究。

文章引用

刘芳琳,邹晨晨. 异方差模型平均的稀疏化赋权
Sparsified Weighting of Heteroscedasticity Model Averaging[J]. 应用数学进展, 2023, 12(08): 3744-3752. https://doi.org/10.12677/AAM.2023.128368

参考文献

1. Andrews, D.W.K. (1991) Heteroskedasticity and Autocorrelation Consistent Covariance Matrix Estimation. Economet-rica, 59, 817-858. https://doi.org/10.2307/2938229

2. Hansen, B.E. and Racine, J.S. (2012) Jackknife Model Averaging. Journal of Econometrics, 167, 38-46. https://doi.org/10.1016/j.jeconom.2011.06.019

3. Liu, Q.F and Okui, R. (2013) Heteroscedasticity-Robust CP Model Averaging. The Econometrics Journal, 16, 463-472. https://doi.org/10.1111/ectj.12009

4. Liu, C.A. (2015) Distribution Theory of the Least Squares Averaging Esti-mator. Journal of Econometrics, 186, 142-159. https://doi.org/10.1016/j.jeconom.2014.07.002

5. Ando, T. and Li, K.C. (2014) A Model-Averaging Approach for Highdimensional Regression. Journal of the American Statistical As-sociation, 109, 254-265. https://doi.org/10.1080/01621459.2013.838168

6. Charkhi, A., Claeskens, G. and Hansen, B.E. (2016) Minimum Mean Squared Error Model Averaging in Likelihood Models. Statistica Sinica, 26, 809-840. https://doi.org/10.5705/ss.202014.0067

7. Zhang, X.Y., Yu, D.L., Zou, G.H. and Liang, H. (2016) Optimal Model Averaging Estimation for Generalized Linear Models and Generalized Linear Mixed-Effects Models. Journal of the American Statistical Association, 111, 1775- 1790. https://doi.org/10.1080/01621459.2015.1115762

8. Zhu, R., Wan, T.K.A., Zhang, X.Y. and Zou, G.H. (2019) A Mallows-Type Model Averaging Estimator for the Varying-Coefficient Partially Linear Model. Journal of the American Statistical Association, 114, 882-892. https://doi.org/10.1080/01621459.2018.1456936

9. Zhao, S.W, Ma, Y.Y., Wan, A.T.K., Zhang, X.Y. and Wang, S.Y. (2020) Model Averaging in a Multiplicative Heteroscedastic Model. Econometric Reviews, 39, 1100-1124. https://doi.org/10.1080/07474938.2020.1770995

10. Zhang, X. and Liu, C.A. (2023) Model Averaging Prediction by K-Fold Cross-Validation. Journal of Econometrics, 235, 280-301. https://doi.org/10.1016/j.jeconom.2022.04.007

11. Zhang, X.Y. and Zou, G.H. (2011) Model Averaging Method and Its Application in Forecast. Statistical Research, 28, 98-103.

期刊菜单