Pure Mathematics
Vol.
11
No.
04
(
2021
), Article ID:
42072
,
14
pages
10.12677/PM.2021.114076
超临界分枝过程的大偏差速率
王小娟,王娟
上海理工大学理学院,上海

收稿日期:2021年3月19日;录用日期:2021年4月21日;发布日期:2021年4月29日

摘要
假设 是带移民的连续时间分枝过程,其中分枝概率是 ,移民概率是 。令 , ( ), , 和 。首先,我们证明 是一个上鞅并且收敛到随机变量K。然后,我们在 和 时,当 和 满足多种矩条件,研究
在t趋于无穷时的衰减速率。
关键词
Q-矩阵,超临界分枝过程,大偏差

Large Deviation Rates for Supercritical Branching Process
Xiaojuan Wang, Juan Wang
Faculty of Science, University of Shanghai for Science and Technology, Shanghai

Received: Mar. 19th, 2021; accepted: Apr. 21st, 2021; published: Apr. 29th, 2021

ABSTRACT
Suppose is the continuous time supercritical branching process with offspring rates and immigration rates . Let , ( ), , and . Firstly, we suppose that is a sub-martingale and converges to a random variable K. Then we study the decay rates of
as
for , under various moment conditions on and .
Keywords:Q-Matrix, Supercritical Branching Process, Large Deviation

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
假设 的取值为非负整数,用 表示t时刻超临界分枝过程的粒子数,则从一个祖先出发的过程可以用以下递归关系表示:
(1.1)
其中 表示t-s时刻第i个个体在t时刻产生的粒子数, 是独立同分布的随机变量,并且具有相同的母函数 , ; 也是i.i.d。并且具有相同的母函数 ,。此外 和 独立。由于我们考虑的是上临界的情况,即是 ,其中 。根据Harris变换 [1],我们可以把 转化为 的情况。所以不失一般性,在之后的文章中我们假设 。
特别地,如果 ,即没有移民加入的情形,那么 退化为上临界分枝过程,记为 ,根据 [2] 可知,存在非负的规范化序列 使得
当 (1.2)
其中 是一个鞅。
如果考虑加入移民,即存在一些时刻s,使得 。根据Seneta [3] 可知,对于(1.2.1)定义的带移民的超临界分枝过程 ,仍存在非负的规范化序列 使得
当 (1.3)
而且,文献 [3] 中还提出超临界分枝过程和带移民的超临界分枝过程的 是相同的,并且满足对 都存在着与 相关的整数 ,满足
(1.4)
其中 , 为非负常数。本文中我们取 。
注1.1根据 [3] 只要移民满足 总能找到规范化函数 ,使其满足式(1.3),而不用对移民分布做任何限制。所以我们默认本文中所取得 都满足式(1.3)。
为了研究方面,我们引入 的Q-矩阵 。
其中:
,,
,。
如果用 来表示带移民的超临界分枝过程 的母函数,则
(1.5)
而且 。
为了叙述的方便,下面我们回忆 已知的衰减速率和收敛性质:
命题1.1 (Liu [4] 和Ney [5] )假设 ,定义
,。
当 时,
(1.6)
上述的收敛对任意的 是一致的,K为 上的任一闭子区间。并且 和 分别满足下列泛函方程:
,,, ;
,,,。
另外, 和 可以分别表示为级数 和 。
由于直接求 的大偏差有些困难,所以在本章的证明中,我们做如下变换:
(1.7)
其中 。
本节我们主要研究 其中引入的移民不全为0。我们关心粒子数 的大偏差,即在 和 满足多种矩条件下,对于 ,和 时研究下列式子的大偏差,
下面是本文的主要定理。
定理1.1 假设对于 , 和 。则对于一些 我们有
(1.8)
其中,
, 是引理2.2中定义的。
定理1.2 假设对于固定的 和 ,存在常数 ,在 和 时满足 和 ,则(1.8)成立。
推论1.1 假设对于 和 ,,则(1.8)成立。
定理1.3 假设对于 和 ,,则存在 满足
定理1.4假设对于 和 ,,则存在 和 满足
2. 预备知识
在开始定理证明之前,我们先介绍一些证明过程中用到的引理或性质,这样可以避免证明的繁琐。
引理2.1假设 , 和 ,如果 存在,则对于 ,我们有
。
引理2.2对于 , 存在,并且当 时, 成立。再者 满足下式:
(2.1)
并且 。
证明:根据Kolmogorov向前方程,
(2.2)
当 时,
也就是
因此
当 时,
也就是
根据引理2.1知:
当 时,
也就是
因此
再者,
因此,
令 ,
注意到,
这里 是独立同分布的并且它的母函数是 , 也是独立同分布的并且它的母函数是 。
性质2.1假设
和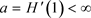 ,
, 是通过
是通过 生成的
生成的 代数。则
代数。则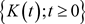 是一个上鞅并且几乎处处收敛到随机变量K。
是一个上鞅并且几乎处处收敛到随机变量K。
证明:根据 的定义可知,对于
的定义可知,对于 ,
,
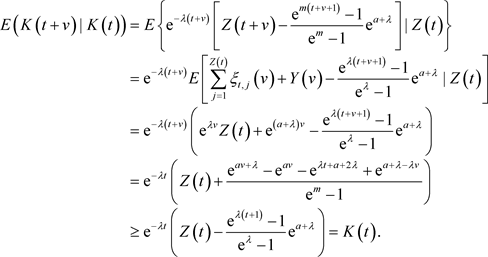
因此 是上鞅。我们知道
是上鞅。我们知道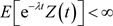 当且仅当
当且仅当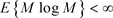 和
和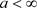 ,所以
,所以 ,则
,则 是一个可积的上鞅,并且几乎肯定收敛到r.v.K。
是一个可积的上鞅,并且几乎肯定收敛到r.v.K。
根据 的定义可知,
的定义可知, 。定义
。定义
 和
和
为了计算的方便,我们将研究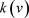 和
和 之间的关系。假设
之间的关系。假设

显然,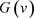 在上增加
在上增加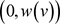 并且
并且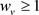 。此外,对于
。此外,对于 ,因为
,因为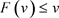 ,我们有
,我们有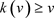 ;对于
;对于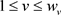 ,因为
,因为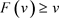 ,我们有
,我们有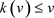 。因此,k的迭代
。因此,k的迭代 在
在 中不增,在
中不增,在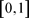 中不减(相对于n)。
中不减(相对于n)。
性质2.2如果 和
和 ,假设
,假设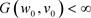 ,则对于
,则对于 ,当
,当 ,
, 并且
并且
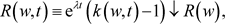 (2.3)
(2.3)
这里的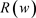 是下式的单根,
是下式的单根,
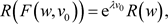 (2.4)
(2.4)
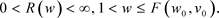 (2.5)
(2.5)
证明:因为 时
时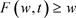 。我们知道对于
。我们知道对于 和
和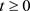 ,
,
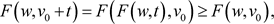
因此 的定义是在
的定义是在 ,并且当
,并且当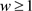 时
时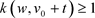 。当
。当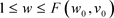 时,因为
时,因为

所以
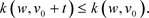
这就意味着当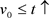 时
时 。定义
。定义 。再者当
。再者当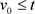 时,
时,
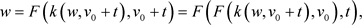
因此
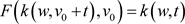 a.s.,
a.s., 
当 时,
时, 。因此我们可知
。因此我们可知 也就是当
也就是当 时
时 。现在,对于
。现在,对于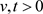 时,存在
时,存在 使得
使得
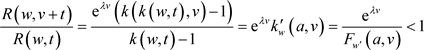
因此,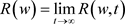 存在。
存在。
再者,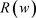 满足(2.3)~(2.5)。所以当
满足(2.3)~(2.5)。所以当

当 时
时
 ,
,
再者
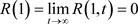 和
和 。
。
因为当 时
时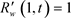 。因此
。因此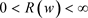 。最后,我们很容易看出(2.3)~(2.5)解的唯一性。
。最后,我们很容易看出(2.3)~(2.5)解的唯一性。
性质2.3假设 时
时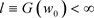 。则
。则
 (2.6)
(2.6)
其中 表示对t取整。
表示对t取整。
证明:当 时,由于
时,由于 ,则
,则
 ,
,
假设 时成立,
时成立,
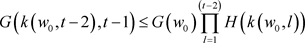 。
。
然后,对于 ,
,

因此(2.6)得证。
3. 定理证明
定理1.1的证明:由于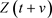 可以定义为:
可以定义为:
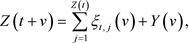 (3.1)
(3.1)
其中 和
和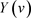 时独立同分布的,因此
时独立同分布的,因此
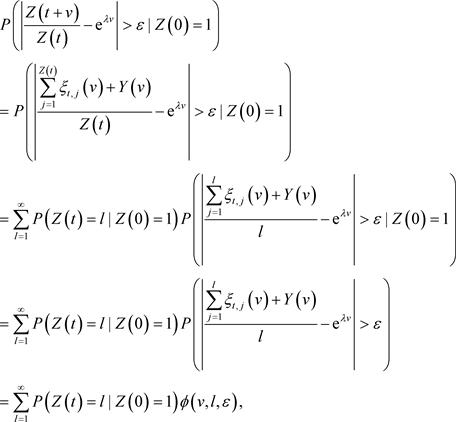
对于固定的 ,
,

其中 和
和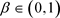 是任意常数。因此
是任意常数。因此

因为 和
和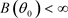 ,所以
,所以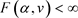 。我们可以得出当
。我们可以得出当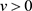 和
和 时,存在
时,存在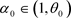 和
和 使得
使得
 和
和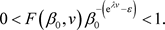
因此存在 和
和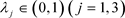 使得
使得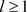 时,
时, 。根据马尔科夫不等式,我们知道存在
。根据马尔科夫不等式,我们知道存在 和
和 ,使得
,使得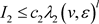 根据引理(2.2),
根据引理(2.2),
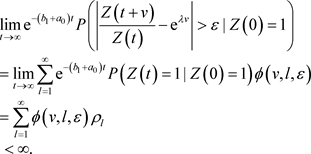
证毕。
定理1.2的证明:当 时,
时,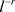 等价于
等价于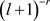 。基于这个事实和定理的假设,对于
。基于这个事实和定理的假设,对于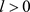 存在另外的
存在另外的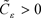 使得
使得 。不失一般性,我们用
。不失一般性,我们用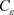 定义
定义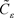 ,因此
,因此

注意到

通过对收敛定理的简单修改,可以证明

当 时,
时,

因此,
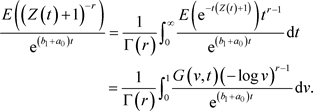
因为 ,如果下式成立则证明将是完整的。
,如果下式成立则证明将是完整的。
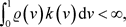 (3.2)
(3.2)
其中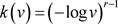 。
。
对于固定的 ,令
,令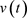 是
是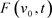 关于
关于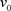 的反函数。可以明显看出当
的反函数。可以明显看出当 时
时 。注意到
。注意到 ,所以,
,所以,

其中

由于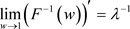 ,而且
,而且 满足
满足

根据假设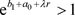 ,则对于
,则对于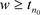 和
和 ,我们能够找到
,我们能够找到 满足
满足 。因此对于
。因此对于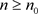 ,
,
 ,
,
这意味着

所以
 (3.3)
(3.3)
当 时,有
时,有
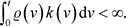 (3.4)
(3.4)
我们可以看出(3.3)和(3.4)暗示着(3.2),证毕。
推论1.1的证明:由于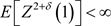 ,对于任意
,对于任意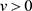 有
有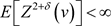 。因此对于
。因此对于 ,存在
,存在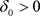 和
和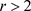 使得
使得 。根据马尔科夫不等式,可得
。根据马尔科夫不等式,可得

根据假设,
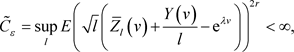
而且对于任意的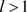 ,存在常数
,存在常数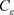 使得
使得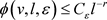 。另外
。另外

定理1.3的证明:不失一般性,我们假设对任意的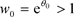 有
有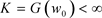 。首先我们证明
。首先我们证明
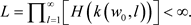 (3.5)
(3.5)
由于 等价于
等价于 ,而且
,而且
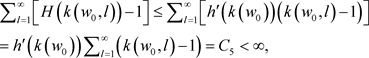
上式中用到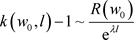 。因此(3.5)成立。根据性质2.3,当
。因此(3.5)成立。根据性质2.3,当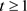 时,
时,
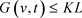 ,
,
再者,当 根据性质2.3
根据性质2.3

由于
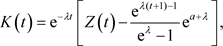

因此当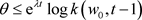 时,
时,

对于 ,当
,当 时我们可得
时我们可得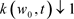 。根据性质2.2
。根据性质2.2

并且上式是正的和有限的。因此我们能找到 使得
使得
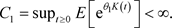
定理1.4的证明:根据定理1.3,我们先给出一个估计。假设当 时
时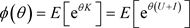 。因此对于
。因此对于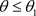 ,
,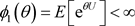 和
和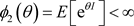 。如果
。如果 是U的独立同分布副本并且
是U的独立同分布副本并且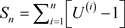 ,I和
,I和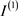 是同分布的变量,则当
是同分布的变量,则当 时,
时,
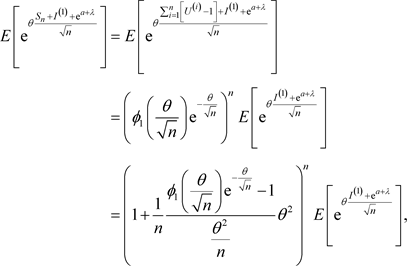
注意到

我们有


令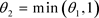 ,则
,则
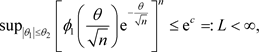
对于 ,我们知道
,我们知道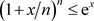 。因此
。因此
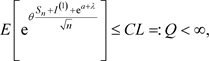
注意到
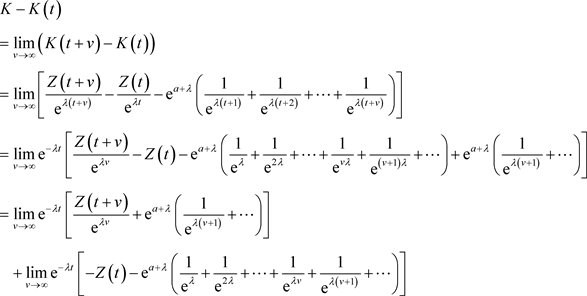

其中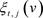 是
是 粒子中第j种粒子在
粒子中第j种粒子在 时刻的种群大小,
时刻的种群大小,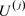 是第j个原始父变量在t时刻下降线上的极限随机变量,
是第j个原始父变量在t时刻下降线上的极限随机变量, 和I是同分布变量。根据独立性可知,
和I是同分布变量。根据独立性可知,

其中,

另外,

因此,
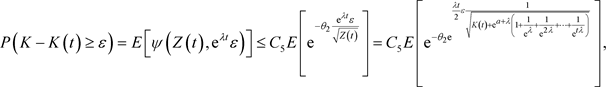
当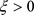 ,
,

因此,

其中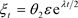 。对于任意的
。对于任意的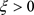 ,
,
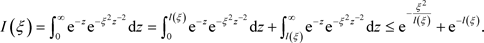
选择 ,则
,则 。因此
。因此

其中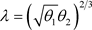 。类似的方法可以证明
。类似的方法可以证明 的成立,证毕。
的成立,证毕。
文章引用
王小娟,王 娟. 超临界分枝过程的大偏差速率
Large Deviation Rates for Supercritical Branching Process[J]. 理论数学, 2021, 11(04): 626-639. https://doi.org/10.12677/PM.2021.114076
参考文献
- 1. Athreya, K.B. and Ney, P.E. (1972) Branching Processes. Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-642-65371-1
- 2. Athreya, K.B. (1994) Large Deviation Rates for Branching Process—I. Single Type Case. The Annals of Applied Probability, 4, 779-790. https://doi.org/10.1214/aoap/1177004971
- 3. Seneta, E. (1970) On the Supercritical Galton-Watson Process with Immigration. Mathematical Biosciences, 7, 9-14. https://doi.org/10.1016/0025-5564(70)90038-6
- 4. Liu, J. and Zhang, M. (2016) Large Deviation for Supercritical Branching Processes. Acta Mathematica Sinica, English Series, 32, 893-900. https://doi.org/10.1007/s10114-016-5437-z
- 5. Ney, P.E. and Vidyashankar, A.N. (2003) Harmonic Moments and Large Deviation Rates for Supercritical Branching Processes. The Annals of Applied Probability, 13, 475-489. https://doi.org/10.1214/aoap/1050689589