Pure Mathematics
Vol.
11
No.
05
(
2021
), Article ID:
42720
,
9
pages
10.12677/PM.2021.115107
完全图去除路P10的图谱特征
林智浩
广东技术师范大学,数学与系统科学学院,广东 广州

收稿日期:2021年4月17日;录用日期:2021年5月20日;发布日期:2021年5月27日

摘要
如果与图G同谱的所有图同构于图G,则称图G是由其图谱所决定的。设 是由完全图 去除图 的边所得到的子图,其中图 是长为 的路。Cámara和Haemers给出猜想1:对于任意的整数 , 可由其邻接谱所决定。本文证明在 的情况下猜想1是正确的。
关键词
图谱,同谱图,谱特征,路

Spectral Characterization of the Complete Graph by Deleting P10
Zhihao Lin
School of Mathematics and System Science, Guangdong Polytechnic Normal University, Guangzhou Guangdong

Received: Apr. 17th, 2021; accepted: May 20th, 2021; published: May 27th, 2021

ABSTRACT
A graph G is said to be determined by its spectrum if any graph having the same spectrum as G is isomorphic to G. Let be the graph obtained from by deleting edges of , where is a path of length . Cámara and Haemers conjectured that is determined by its adjacency spectrum for every . In this paper, we show that the conjecture is true for .
Keywords:Graph Spectrum, Cospectral Graphs, Spectral Characterization, Path

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文所考虑的图都是无向、有限的简单图,即是不包含环和多重边的图。图谱中的一些符号和定义,请参阅文献 [1]。
设 ,其点集和边集分别记为 和 。设 是图G的(0, 1)邻接矩阵,图G的特征多项式记为 。图G的图谱包含了图G的所有特征值(包含重数)。如果两个图有一样的邻接谱,那么称这两个图同谱。如果任何与图G具有相同谱的图与图G同构,则称图G是由其谱所决定的(简称DS)。
图谱能够反映出图的一些有用的组合信息。图谱理论中的一个基本问题是“哪些图是DS?”。这个问题起源于化学,可以追溯到60多年前。而在近些年来,它受到了研究者的广泛关注。
然而,证明一个图是DS通常是一个非常困难的问题。到目前为止,很少有一类具有特殊结构的图被证明是DS。通常情况下,DS的图只包含有很少数的边,如T形树图 [2]、 图 [3]、棒糖图 [4] 和 图 [5] 等等。对于含有大量边的稠密图,这通常很难证明他们是DS。比如在文献 [6] 中,一条路的补图 被证明是DS,但是这个证明远比证明路 是DS涉及的多。关于这一问题的更多背景可以参阅文献 [7] [8]。
在文献 [9] 中,Cámara和Haemers等人研究了在完全图下删除了其中的一些边后所得到的图是DS。 为一条长为 的路, 为 阶的完全图。在 中删除掉路 的边所得到的图记为 。他们给出了以下的猜想:
猜想1 (Cámara和Haemers [9] )对于任意的整数 满足 , 是DS。
在文献 [9] 中,作者已经证明了在 时猜想1是正确的。当 时,也被证明了猜想1是正确的,这也是文献 [3] 中的主要结果。Mao,Cioabǎ和Wang在文献 [10] 中证明了当 时,猜想1是正确的。本文证明了在 时,猜想1是正确,即:
定理1.1 当 时,图 是DS。
在第二部分中,将给出一些重要的引理及其证明。在第三部分中给出了定理1.1的证明。本文总结和进一步的研究问题将会在第四部分给出。
2. 一些引理的介绍和证明
在这一部分中,将给出证明定理1.1所需要的一些引理。
引理2.1 (van Dam和Haemers [7] )图G的下列性质可以从邻接谱推导出来:
1) 顶点的数量;
2) 边的数量;
3) 固定长度的闭途径数量。
引理2.2 (Mao,Cioabǎ和Wang [11] )设 为在图G中与图H同构的子图(不一定是诱导)的数目, 为图G中长为i的闭途径数目。设 为经过图H所有边且长为i的闭途径数目, 为图G中所有连通子图H的集合,其中 。这可以得出 为
。
引理2.3 (Omidi [11] )以下给出的是图G中长为2、3、4、5的闭途径的数目:
1) ,。
2) ;。
其中m为G的边数,图 为圈图 上任一个顶点加上一条边得到的图(见图2(a))。
引理2.4 (Cvetković,Doob和Sachs [1] )设图G中k-闭途径的数量为c,那么该数量可以由其邻接谱决定,即
。
设n阶图G的邻接谱为 ,n阶图 的邻接谱为 。众所周知,若 ,,那么有
。
也就是两个图的邻接谱相同,那么它们的各特征值的k次方和也相等,所以可以得到当
,
则有 与 不全相等, 。因此结合引理2.4,可以得到这么一个结论:当两个阶数相同的图的k-闭途径数量(k为正整数)不相同时,则它们的邻接谱不相同,即这两个图不同谱。引理2.5~2.7分别给出了当 时,图G补图中k-闭途径数量的计算方法。
引理2.5 (Doob和Haemers [6] )设图G有n个顶点,m条边,t个子图 和其度序列为 。设 为图G补图的子图 数量。则有
。
引理2.6 (Cámara和Haemers [9] )设图G有n个顶点,m条边,其补图4-闭途径的数量由图G的顶点和边的数量以及图G中同构于 ,, 和 的子图(不一定是诱导)数量所决定,分别用 ,, 和 表示,以及将图 中4-闭途径的数量表示为 ,则图G补图中的4-闭途径数量等于
,
其中
研究长为5的闭途径的情况会更加的困难,将由以下引理提出。
引理2.7 (Mao,Cioabǎ和Wang [10] )设图G有n个顶点、m条边,其补图5-闭途径的数量由图G的顶点和边的数量,以及图G中同构于 ,,,,,,, 和 的子图(不一定是诱导)数量所决定,分别用 ,,,,,,, 和 表示,以及将图 中5-闭途径的数量表示为 ,则图G补图中的5-闭途径数量等于
。
其中
设H为有 条边的简单图,下文将用 ,,,,,,, 和 表示图 中同构于 ,,,,,,,, 和 的子图数量,用 ,,,,,,, 和 表示图H中同构于 ,,,,,,, 和 的子图数量。
在给出和证明以下引理之前,先对几类特殊图进行符号的规定。符号 表示为图1(a)所示的图例,其中a,b,c代表三条支路对应边的数量,且满足 ,如图1(d)表示为 。符号 表示为图1(b)所示的图例,其中a,b,c,d代表四条支路对应边的数量,且满足 ,如图1(e)表示为 。符号 表示为图1(c)所示图例,其中a,b,c,d代表四个位置对应边的数量,且满足 ,,如图1(f)表示为 。
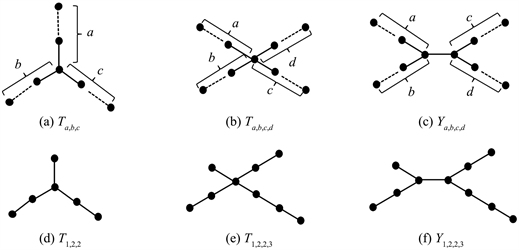
Figure 1. Special graphs of several types
图1. 几类特殊图
引理2.8 (Mao,Cioabǎ和Wang [10] )以下的三类图均与图 不同谱
1) 对于任意的整数 时,图 和 不同谱。
2) 对于任意的整数 , 且满足 时,图 和 不同谱。
3) 对于任意的整数 ,,, 且满足 时,两类图 和 不同谱。
引理2.9 对于任意的整数 ,,, 且满足 时,两类图 和 不同谱。
证明:图 可以直接计算得出
对于图 ,有
由 可得 ,又因为 ,则
利用引理2.6,可以直接得出,图 和图 可以通过4-闭途径的数量来区分。£
引理2.10 对于任意的整数 , 且满足 时,两类图 和 不同谱,其中图 表示为含有b条边的树。
证明:图 可以直接计算得出
对于图 ,, 和 ,有
图 和图 在n个顶点下的补图分别为图 和图 ,由引理2.6可知,这两类图可以通过4-闭途径的数量来区分,则不同谱。 £
引理2.11 (Mao,Cioabǎ和Wang [10] )设图 与图 同谱,则图H中子图 数量 为偶数。
引理2.12 (Mao,Cioabǎ和Wang [10] )设图 与图 同谱。那么图H有以下三个性质。
1) 除了 和 ,图H的任何部分都不是圈。
2) 图H不包含两个不相交的圈 。
3) 除了 之外,图H包含两条长度不相等的路径。
3. 定理1.1的证明
设图 为 的补图,则图G有n个顶点, 条边,不含子图 ,并且其度序列为 。因此, 中的子图 数量 为
.
设图 为 的补图,则其有n个顶点, 条边, 个子图 ,度序列为 。那么图 中子图 数量 为
.
设图 和图 同谱,则两图含有相同数量的子图 。而且由于删去了相同数量的边,那么删去的度数也是相等。因此有
(1)
定理1.1的证明:当 时,图H含有9条边,其最多含有7个子图 ,则有
. (2)
当 , 时,有 ,当 时不成立,所以k最大取6,则有
. (3)
对于 取值范围确定,当 时,由
和
,
可以得到
. (4)
结合式子(1)-(4),及Matlab计算,可以得到组合 的所有情况如下:
有这样一组参数 ,如果存在一个与该参数相同的图,那么称这组参数为该图的图解。实际上,并不是所有的这些参数组合都是图解,有部分是不符合图条件要求的。并且这些有效的图解中可能存在多个图的表示。如表1所示,这里只给出有效图解的组合和其相对应的图(表1中相关的子图见图2)。
根据引理2.8~2.12,除了图 、、和 以外,这里剩余的所有图的 都与 不同谱。接下来将计算在这三个图中4-闭途径的数量,并在表2中给出它们各子图的数量。
对于图 ,直接计算得
Table 1. Complements of all possible K n \ H of the same spectrum as K n \ P 10
表1. 所有可能与 同谱的 的补图
Table 2. The number of related subgraphs of H
表2. 图H的相关子图数量
通过表2中图H与图 的各子图数量对比,以及引理2.6,则这三个图作为H时,图 与图 有不同数量的4-闭途径,因此它们不同谱。综上所述,证得图 是DS。定理1.1得证。 £

Figure 2. Some related subgraphs
图2. 文中涉及到的一些相关子图
4. 小结
在本文中,主要利用图 的邻接谱性质,通过对与图 可能同谱的图做详细的分类,并且计算图的4-闭途径和5-闭途径的数量是否相同,来得到他们是否同谱,从而证明在l取值较小的情况下图 是DS。但在取较大值的l时,与 可能同谱的图的详细分类会非常的复杂和繁琐,运用以上的方法是不理想的。因此,要证明猜想1在一般情况是正确,需要新的方法和工具。
致谢
感谢审稿人对本文提出的修改意见,并感谢游志福教授在本篇文章的写作过程中给予指导。
文章引用
林智浩. 完全图去除路P10的图谱特征
Spectral Characterization of the Complete Graph by Deleting P10[J]. 理论数学, 2021, 11(05): 937-945. https://doi.org/10.12677/PM.2021.115107
参考文献
- 1. Wang, W. and Xu, C.X. (2006) On the Spectral Characterization of T-Shape Trees. Linear Algebra and Its Applications, 414, 492-501. https://doi.org/10.1016/j.laa.2005.10.031
- 2. Liu, F., Huang, Q., Wang, J. and Liu, Q. (2012) The Spectral Characterization of ∞-Graphs. Linear Algebra and Its Applications, 437, 1482-1502. https://doi.org/10.1016/j.laa.2012.04.013
- 3. Haemers, W.H., Liu, X.G. and Zhang, Y.P. (2008) Spectral Char-acterization of Lollopop Graphs. Linear Algebra and Its Applications, 428, 2415-2423. https://doi.org/10.1016/j.laa.2007.10.018
- 4. Ramezani, F., Broojerdian, N. and Tayfeh-Rezaie, B. (2009) A Note on the Spectral Characterization of θ-Graphs. Linear Algebra and its Applications, 431, 626-632. https://doi.org/10.1016/j.laa.2009.03.013
- 5. Doob, M. and Haemers, W.H. (2002) The Complement of the Path Is Determined by Its Spectrum. Linear Algebra and Its Applications, 356, 57-65. https://doi.org/10.1016/S0024-3795(02)00323-3
- 6. Dam, E.R.V. and Haemers, W.H. (2003) Which Graphs Are Determined by Their Spectrum? Linear Algebra and Its Applications, 373, 241-272. https://doi.org/10.1016/S0024-3795(03)00483-X
- 7. Dam, E.R.V. and Haemers, W.H. (2009) Developments on Spectral Characterizations of Graphs. Discrete Mathematics, 309, 576-586. https://doi.org/10.1016/j.disc.2008.08.019
- 8. Cámara, M. and Haemers, W.H. (2014) Spectral Characterization of almost Complete Graphs. Discrete Applied Mathematics, 176, 19-23. https://doi.org/10.1016/j.dam.2013.08.002
- 9. Cvetković, D.M., Doob, M. and Sachs, H. (1980) Spectra of Graphs. Academic Press, New York.
- 10. Mao, L.H., Cioabă, S.M. and Wang, W. (2019) Spectral Characterization of the Complete Graph Removing a Path of Small Length. Discrete Applied Mathematics, 257, 260-268. https://doi.org/10.1016/j.dam.2018.08.029
- 11. Omidi, G.R. (2009) On a Signless Laplacian Spectral Characteri-zation of T-Shape Trees. Linear Algebra and Its Applications, 431, 1607-1615. https://doi.org/10.1016/j.laa.2009.05.035
