Pure Mathematics
Vol.
12
No.
01
(
2022
), Article ID:
48370
,
14
pages
10.12677/PM.2022.121023
线性矩阵不等式半定互补问题的数值求解方法
孔汕汕,赵馨*
东华大学理学院,上海
收稿日期:2021年12月18日;录用日期:2022年1月20日;发布日期:2022年1月27日

摘要
线性矩阵不等式半定互补问题是一类新颖的多项式优化问题,是半定规划与互补问题的交叉研究内容。该问题可以转化为一系列带有线性矩阵不等式约束的多项式优化子问题,进而可以采用标量型松弛方法或矩阵型松弛方法进行求解。更进一步,当线性矩阵不等式半定互补问题的实数解个数有限时,利用本文给出的算法可以计算出该问题的全部实数解。最后,我们进行相关数值实验,分别使用标量型松弛方法和矩阵型松弛方法求解该问题,并将这两种方法的结果进行对比。
关键词
半定互补问题,线性矩阵不等式,标量型松弛方法,矩阵型松弛方法

Numerical Methods for the Semidefinite Complementarity Problem with Linear Matrix Inequalities
Shanshan Kong, Xin Zhao*
College of Science, Donghua University, Shanghai
Received: Dec. 18th, 2021; accepted: Jan. 20th, 2022; published: Jan. 27th, 2022

ABSTRACT
The semidefinite complementarity problem with linear matrix inequalities is a novel polynomial optimization problem, which is the cross-study content of semidefinite programming and complementarity problems. The problem can be transformed into a series of polynomial optimization subproblems with linear matrix inequality constraints. Then the problem can be solved by the scalar-type relaxation method or the matrix-type relaxation method. Furthermore, when the number of real solutions of the semidefinite complementarity problem with linear matrix inequalities is limited, all real solutions of the problem can be calculated by using the algorithm given in this paper. Finally, we conduct related numerical experiments. We use the scalar-type relaxation method and the matrix-type relaxation method to solve the problem and compare the results of these two methods.
Keywords:Semidefinite Complementarity Problem, Linear Matrix Inequalities, Scalar-Type Relaxation Method, Matrix-Type Relaxation Method

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
线性矩阵不等式(linear matrix inequalities, LMI)一般描述为:
其中 , , , 是对称矩阵,矩阵 是一个从n维实数空间到 维实对称矩阵空间的映射,矩阵中的每一个元素都是以 为变量的多项式。矩阵 表示矩阵 是正定的,即对任意的 ,有 。近年来,线性矩阵不等式得到了越来越多的关注和重视,被广泛地应用于解决控制中的问题,已经成为系统与控制领域研究中的一大热点研究内容 [1] [2]。
本文考虑带有线性矩阵不等式约束的半定互补问题:寻求解 满足 , , ,其中 是线性矩阵不等式。线性矩阵不等式半定互补问题是一种新的半定互补问题,目前很少有关于这个问题的相关文献和理论结果。线性矩阵不等式半定互补问题可以看作标量型多项式互补问题的推广,这两个问题显著的区别是在线性矩阵不等式半定互补问题中涉及到矩阵型约束,而不仅仅是标量型约束。这里所说的“矩阵型”是指多项式矩阵不等式约束,“标量型”是指单个多项式不等式约束。
求解带有 的半定约束问题的一类直观方法是将其转化为若干个标量的不等式约束。例如,将线性矩阵不等式约束 转化为 的顺序主子式大于等于0,进而将矩阵型约束转化为标量型约束,继而可以采用传统的标量型松弛方法进行求解,如采用经典的Lasserre松弛方法 [3] 进行求解。Lasserre松弛方法是基于半定规划松弛的,通过构造一系列半定规划松弛问题,可以无限逼近原多项式优化问题的全局最优值。Lasserre证明了当阿基米德条件成立时,该松弛方法具有渐进收敛性。但是,当 的维数很大时,此类方法可能会导致大量的高次约束,导致松弛问题的规模过大,从而使得不适合采用标量型松弛方法进行求解。因此,许多学者致力于直接研究带有多项式矩阵约束的优化问题。例如,Hol等 [4] [5] 和Kojima [6] 对多项式矩阵平方和分解进行了深入的研究。为了求解非凸多项式矩阵不等式优化问题,Henrion等 [7] 利用Hol等 [4] [5] 和Kojima [6] 关于非负多项式矩阵平方和分解的矩理论的研究成果,将标量型松弛方法推广到了求解非凸多项式矩阵不等式优化问题的矩阵型松弛方法。Henrion等 [7] 指出当阿基米德条件成立时,该矩阵型松弛方法具有渐进收敛性。
此外,Nie [8] 给出了利用半定松弛方法来计算一个多项式的局部极小值的层次结构算法。下面我们以在无约束情况下求一个多项式的局部极小值为例对该方法进行说明。具体方法如下:任意给定一个多项式
,利用最优性条件
,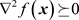 构造半定松弛问题并定义H-最小值点以及H-最小值,然后通过构造并求解一系列半定松弛问题,可以将全部的H-最小值点以及H-最小值计算出来,最后可以从这些值中找出
的全体局部极小值,且Nie证明了构造的这一系列松弛问题都具有有限收敛性。
构造半定松弛问题并定义H-最小值点以及H-最小值,然后通过构造并求解一系列半定松弛问题,可以将全部的H-最小值点以及H-最小值计算出来,最后可以从这些值中找出
的全体局部极小值,且Nie证明了构造的这一系列松弛问题都具有有限收敛性。
利用线性矩阵不等式的性质 [9] [10],我们可以将线性矩阵不等式半定互补问题进行等价改写,得到与该问题等价的矩阵形式的问题,进而可以采用矩阵型松弛方法进行求解。进一步,当线性矩阵不等式半定互补问题的实数解个数有限时,利用层次结构算法的思想可以计算出该问题的全部实数解。
符号说明:符号 ( )表示非负整数集(实数集)。符号 表示n维非负整数向量集合。符号 表示n维实向量集合。对于 , 表示 中的第i个元素,即 。对于 ,令 。对于 及 ,令 。对于整数 , 表示集合 。对于任意整数 , 表示不小于t的最小整数。上标T表示矩阵或向量的转置。对于多项式 , 表示它的次数。符号 表示 维实对称矩阵空间。符号 表示在实数域上以 为自变量的多项式环,即任意 是一个以 为自变量的多项式。令 是指由次数至多为k的 中的多项式构成的集合,即 。令 表示 维实对称多项式矩阵空间,即任意 , 是一个对称多项式矩阵且每一项 是一个以 为自变量的多项式。如果对于任意非零向量 ,二次型 是非负的,则称矩阵 是正定的,记作 。一个多项式矩阵 的次数 是矩阵中全部元素所代表的多项式中的最大次数,即 。令 表示两个向量或矩阵的标准内积。
2. 线性矩阵不等式半定互补问题的等价改写
本节研究如何等价地改写线性矩阵不等式半定互补问题:给定矩阵 , ,寻求解 满足 , , ,其中 是线性矩阵不等式。记该问题的全体实数解构成的集合为 ,则
(1)
根据线性代数的知识可以得到:对于两个半正定矩阵 , 当且仅当 。因此,线性矩阵不等式半定互补问题中的互补条件等价于矩阵型等式约束,即:
(2)
令 是 维多项式矩阵,其中 ,则 。令标量多项式 ,则有多项式组 。因此,可以得到
(3)
由公式(3)可以看出,集合 的定义中涉及了线性矩阵不等式约束 和 。此前,对于这类约束的优化问题的求解较为困难。事实上,一类处理方法是我们可以将线性矩阵不等式约束转化为标量型约束,从而用一系列标量型不等式约束来描述集合 。例如:当 的维数大于2时, 当且仅当它的各阶顺序主子式大于等于零 [11],即:对于 , 等价于 ,其中 为 的第j阶顺序主子式,则可以得到 的等价形式:
(4)
特别地,当 的维数等于2时, 当且仅当 且 ,则
由公式(4)中可以看出,当原问题的规模较大时,标量化改写方法会引入大量的高次约束,导致松弛问题的规模过大,从而变得难以求解。因此我们考虑保留线性矩阵不等式半定互补问题的矩阵型约束进行计算。
由文献 [9] 可知,线性矩阵不等式约束序列 等价于一个线性矩阵不等式约束 。
令 ,则
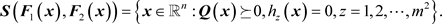 (5)
(5)
由公式(4)和(5)可知,通过随机地选取一个恰当的多项式 作为目标函数,我们可以将原线性矩阵不等式半定互补问题的解集分别转化为下列两种形式的多项式优化问题的可行域,其中标量型多项式优化问题为:
(6)
矩阵型多项式优化问题为:
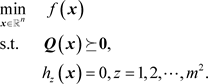 (7)
(7)
显然, 当且仅当 是问题(6)或(7)的一个可行解。
3. 求解全体实数解的层次结构方法
本节中,我们将研究线性矩阵不等式半定互补问题的层次结构方法,假设实数解的个数有限,我们将给出求解该问题的全体实数解的方法。
首先,我们考虑在问题(6)和问题(7)中选取目标函数 。事实上,通过适当地选取,多项式 在 的不同的解处取得不同的函数值,将这些值依次排列 ,称 是第i个可行值。
令第i个解集合为 ,则解集合 能被划分为有限多个互不相交的非空子集,即 。
若我们可以将解集合 全部求解出来,则可以计算出原问题的全部实数解。下面我们分别构造与每一个子集合 相对应的优化子问题,进而求解出所有的 。此处类比Nie在文献 [8] 中求解多项式的局部极小值的层次结构算法完成这项工作。
显然,第一个解集合 是第2节中构造的两个多项式优化问题(6)和(7)的最优解的集合,即,标量型优化问题
(8)
和等价的矩阵型优化问题
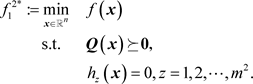 (9)
(9)
如果问题(8)或问题(9)是可解的,则可以得到问题的最优值,在不需要对比两种方法时,为了方便叙述都将其记为 ,称问题(8)或问题(9)是第一个子问题。
获得了可行值 和相应的可行集 之后,进一步构造并求解下一个子问题以求解第二个可行集 。依次进行下去,每一步在求解出可行值 和相应的可行集 之后,构造并求解下一个子问题以求解可行集 ,最终可以求解出全部可行集 。具体的方法如下:在获得了前t个可行值 和相应的可行集 之后,构造第 个子问题,其中第 个标量型子问题为:
(10)
第 个矩阵型子问题为:
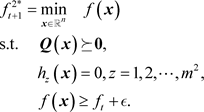 (11)
(11)
其中问题(10)和问题(11)中使用的参数 是满足
(12)
的一个正数。当第 个子问题可解时,无论标量型问题(10)还是等价的矩阵型问题(11),在不需要对比两种方法时,为了方便叙述都将其最优值记为 ,在需要对比两种方法时,我们将这两个最优值分别记为 和 。
引理3.1 当且仅当参数 满足条件(12)。
证明:如果 满足条件(12),则 。又因为 是 上大于或等于 的最小可行值,则 。反之,如果 ,则表明在 上存在可行值,所以,若 存在,则必有 ,即参数 满足条件(12)。
但是,考虑到 是否存在是未知的,即便知道其存在,也很难提前去确定它的值。在实际计算过程中,参数 的取值不宜过小,以免在数值计算过程中导致结果产生较大偏差。因此,我们需要考虑如何找到合适的参数 来构造第 个子问题(10)或(11)。为了解决这一问题,我们分别构造第 个判定优化子问题:即标量型判定问题
(13)
和矩阵型判定问题
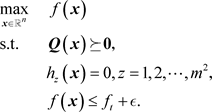 (14)
(14)
明显地,上述两类判定优化子问题都是可解的,因为任意 都是它的可行解,我们将问题(13)和问题(14)的最优值记为 ,则有下列结果成立。
引理3.2对于 , 当且仅当 。
证明:如果 ,则 ,由问题(13)或(14)可知, 是 上小于或等于 的最大可行值,则 。反之,如果 ,则表明在 上不存在可行值,所以,如果 存在,则必有 ,即 成立。
事实上, 的值不能取太小,例如0.05是符合计算上的要求的。在问题(13)或问题(14)中,令 。如果 ,我们将 减小至 ,再次求解问题(13)或问题(14),重复这个过程直至 ,我们即可得到合适的参数 的值。
利用引理3.2的结果,我们可以确定适当的参数 ,利用该参数 和当前可行值 ,我们可以构造下一个子问题,参考公式(10)和(11)。如果下一个子问题不可行,则说明下一个可行值 不存在,即 是线性矩阵不等式半定互补问题的所有的可行值中的最大值。否则,若 存在且 满足条件(12),通过求解第 个子问题可以得到下一个可行集 。至此,我们给出了线性矩阵不等式半定互补问题的层次结构方法。若我们能够求解出标量型子问题序列(10)和矩阵型多项式优化子问题序列(11),以及它们对应的判定问题序列(13)和(14),即可求解出原问题的全部实数解。
4. 半定松弛算法及其收敛性
在前两节的内容中,我们利用层次结构方法将线性矩阵不等式半定互补问题转化为标量型多项式优化子问题序列(8),(10),(13)或矩阵型多项式优化子问题序列(9),(11),(14)。本节中,我们对这两类多项式优化子问题分别给出半定松弛求解方法,从而完成对原问题的求解。
4.1. 求解标量型多项式优化子问题的半定松弛方法
对于标量型子问题序列(8),(10)和(13),我们采用Lasserre在文献 [3] 中提出的经典半定松弛方法进行求解。
首先,我们需要定义局部化矩矩阵。令 和 分别是 和 的一组基,其中 , 是它的维数。令 是一个矩序列, 是任意一个多项式,定义Riesz函数 : 。如果给定一个截断矩序列 ,定义关于 的k阶矩矩阵为 。对于标量多项式 ,定义由截断矩序列 生成的关于多项式 的k阶局部化矩矩阵为 ,其中 。
如果一个截断矩序列 满足下面的条件:
(15)
其中 ,则称 满足平滑条件。若 满足平滑条件(15),则 在半代数集
上存在唯一的一个s-原子表示测度。
接下来,我们给出矩阵型子问题序列(8),(10)和(13)的求解方法。例如,采用Lasserre松弛方法求解问题(10)时,创建问题(10)的k阶松弛如下:
(16)
其中 , ,且
是最低松弛阶数。
令 是由多项式组 生成的理想的第2k阶截断,即
是由 和 生成的二次模块的第k阶截断,即
问题(16)的对偶是:
(17)
半定规划问题(16)和问题(17)是对偶问题。因此,对于多项式优化问题(10),可以采用原对偶内点方法 [12] 求解相应的松弛问题。通过求解一系列松弛问题(16),可以得到序列 ,随着松弛阶数增大, 逐渐逼近于多项式优化问题(10)的最优值。问题(8)和(13)可以采用类似的方法进行求解。
4.2. 求解矩阵型多项式优化子问题的半定松弛方法
对于矩阵型子问题序列(9),(11)和(14),我们采用矩阵型半定松弛方法进行求解。类似于标量型Lasserre半定松弛方法,我们参考Henrion等在文献 [7] 中提出的矩阵型松弛方法。首先,定义由矩阵 生成的局部化矩矩阵为 ,其中 , 表示Kronecker积。
如果一个截断矩序列 满足下面的条件:
(18)
其中 ,则称 满足平滑条件。若 满足平滑条件(18),则 在半代数集
上存在唯一的一个s-原子表示测度。
接下来,我们给出矩阵型子问题序列(9),(11)和(14)的求解方法。例如,采用矩阵型松弛方法求解问题(11)时,创建问题(11)的k阶松弛如下:
(19)
其中 , ,且
是最低松弛阶数。
令 是由多项式组 生成的理想的第2k阶截断,即
是由 和 生成的二次模块的第k阶截断,即
问题(19)的对偶是:
(20)
半定规划问题(19)和问题(20)是对偶问题。因此,对于多项式优化问题(11),可以采用原对偶内点方法 [12] 求解相应的松弛问题。通过求解一系列松弛问题(19),可以得到序列 ,随着松弛阶数增大, 逐渐逼近于多项式优化问题(11)的最优值。问题(9)和(14)可以采用类似的方法进行求解。
4.3. 算法
下面,我们给出求解线性矩阵不等式半定互补问题的全体实数解的半定松弛算法。
算法4.3.1:求解线性矩阵不等式半定互补问题的标量型算法
步骤1. 随机地选取一个多项式 作为目标多项式。令 , 。符号 表示线性矩阵不等式半定互补问题的解集, 表示可行值构成的集合。
步骤2. 若问题(8)的松弛问题是不可行的,则令 ,停止。否则,求解问题(8)的松弛问题,得到最优解 和最优值 。
步骤3. 若存在某个 ,截断矩序列 满足平滑条件(15),则令 ,其中 是问题(8)的最优解的集合。令 , , ,转向步骤4。若不存在这样的s,则令 ,转向步骤2。
步骤4. 令 ,计算问题(13)的最优值 。若 ,则令 ,再次求解问题(13),重复这个过程直至 。
步骤5. 求解问题(10)的松弛问题。若它不可行,则没有更多的实数解,令 ,其中 ,停止;否则,求解问题(10)的松弛问题得到最优解 和最优值 。
步骤6. 若存在某个 ,截断矩序列 满足平滑条件(15),则更新 ,其中 是问题(10)的最小值点的集合。令 , , ,转向步骤4。若不存在这样的s,则令 ,转向步骤5。
算法4.3.2:求解线性矩阵不等式半定互补问题的矩阵型算法
步骤1. 随机地选取一个多项式 作为目标多项式。令 , 。符号 表示线性矩阵不等式半定互补问题的解集, 表示可行值构成的集合。
步骤2. 若问题(9)的松弛问题是不可行的,则令 ,停止。否则,求解问题(9)的松弛问题,得到最优解 和最优值 。
步骤3. 若存在某个 ,截断矩序列 满足平滑条件(18),则令 ,其中 是问题(9)的最优解的集合。令 , , ,转向步骤4。若不存在这样的s,则令 ,转向步骤2。
步骤4. 令 ,计算问题(14)的最优值 。若 ,则令 ,再次求解问题(14),重复这个过程直至 。
步骤5.求解问题(11)的松弛问题。若它不可行,则没有更多的实数解,令 ,其中 ,停止;否则,求解问题(11)的松弛问题得到最优解 和最优值 。
步骤6.若存在某个 ,截断矩序列 满足平滑条件(18),则更新 ,其中 是问题(11)的最小值点的集合。令 , , ,转向步骤4。若不存在这样的s,则令 ,转向步骤5。
对于Lasserre松弛方法 [3],Lasserre证明了在阿基米德条件成立时,该松弛方法具有渐进收敛性。Henrion等 [7] 利用非负多项式矩阵平方和分解的相关理论结果,将标量型松弛方法进行推广,得到了矩阵型松弛方法,并证明了在阿基米德条件成立时,该矩阵型松弛方法同样具有渐进收敛性。因此,通过文献 [3] 和 [7] 的相关结论,可以得到算法4.3.1和算法4.3.2的收敛性定理如下:
定理4.3.3假设线性矩阵不等式半定互补问题的实数解个数有限,则当松弛阶数 时, 。
根据定理4.3.3可知:当线性矩阵不等式半定互补问题的实数解个数有限时,算法4.3.1和4.3.2具有渐进收敛性。
5. 数值实验
本节将给出求解线性矩阵不等式半定互补问题的数值实验结果。下表中的运行时间是每个维度20次的平均运行时间,时间结果保留四位小数。我们分别用下面的两种方法求解线性矩阵不等式半定互补问题:
方法1 (标量型方法):采用直观的标量化方法,将原问题中的半定约束转化为由顺序主子式组成的约束。将原问题等价转化为子问题序列(8)、(10)和(13),再采用上一节的算法4.3.1进行求解。
方法2 (矩阵型方法):保留线性矩阵不等式半定互补问题的矩阵形式进行计算。将原问题等价转化为子问题序列(9)、(11)和(14),再采用上一节的算法4.3.2进行求解。
在数值实验部分,我们使用的是操作系统是Windows10,内存是8.0 GB RAM,处理器是Inter(R)Core(TM)i58265U@1.80 GHz的笔记本电脑。我们调用Matlab R2014b软件,使用YALMIP [13],SeDuMi [14] 和Gloptipoly 3 [15] 求解线性矩阵不等式半定互补问题。
例1. 给定多项式矩阵
考虑线性矩阵不等式半定互补问题: , , 。设目标函数为 。
记:Pi:求解第i个子问题至达到收敛所需要的松弛次数;Si:第i个子问题的松弛问题中半定不等式约束的规模。下表中的分号是用于分隔在不同松弛阶数的松弛问题中的数据。为了方便表示,下表中松弛问题的规模Si用数字表示,例如数字5表示的是在松弛问题中有一个5 × 5的矩阵。我们分别用方法1和方法2求解该问题,求解结果见表1和表2:
Table 1. Solution, calculation time of the problem and relaxation times of the ith subproblem
表1. 问题的解、计算时间以及第i个子问题的松弛次数
Table 2. The scale of semidefinite inequality constraints in the relaxation problem of the ith subproblem
表2. 第i个子问题的松弛问题中半定不等式约束的规模
例2. 给定多项式矩阵
考虑线性矩阵不等式半定互补问题: , , 。设目标函数为 。下表中的各个量以及符号所表示的含义与例1相同。我们分别用方法1和方法2求解该问题,求解结果见表3和表4:
Table 3. Solution, calculation time of the problem and relaxation times of the ith subproblem
表3. 问题的解、计算时间以及第i个子问题的松弛次数
Table 4. The scale of semidefinite inequality constraints in the relaxation problem of the ith subproblem
表4. 第i个子问题的松弛问题中半定不等式约束的规模
例3. 给定多项式矩阵
考虑线性矩阵不等式半定互补问题: , , 。设目标函数为 。下表中的各个量以及符号所表示的含义与例1相同。我们分别用方法1和方法2求解该问题,求解结果见表5和表6:
Table 5. Solution, calculation time of the problem and relaxation times of the ith subproblem
表5. 问题的解、计算时间以及第i个子问题的松弛次数
Table 6. The scale of semidefinite inequality constraints in the relaxation problem of the ith subproblem
表6. 第i个子问题的松弛问题中半定不等式约束的规模
注:在例3中,方法2的第一和第二个子问题在最低阶松弛阶数时不收敛,因此我们需要求解5个半定问题,方法1的三个子问题都在最低阶松弛阶数时收敛,所以只需要求解3个半定问题。因为求解半定问题占据了大量的计算量,所以在例3中方法2的计算时间大于方法1。
例4. 给定多项式矩阵
考虑线性矩阵不等式半定互补问题: , , 。设目标函数为 。下表中的各个量以及符号所表示的含义与例1相同。我们分别用方法1和方法2求解该问题,求解结果见表7和表8:
Table 7. Solution, calculation time of the problem and relaxation times of the ith subproblem
表7. 问题的解、计算时间以及第i个子问题的松弛次数
Table 8. The scale of semidefinite inequality constraints in the relaxation problem of the ith subproblem
表8. 第i个子问题的松弛问题中半定不等式约束的规模
通过上面的数值实验的结果可以发现:虽然这两种方法一般都可以求解出线性矩阵不等式半定互补问题的全部实数解,但是这两种方法的求解效果却不同。下面给出这两种方法的数值实验结果的对比:
1) 一般情况下,方法2比方法1消耗时间较少,这是因为在用方法1时,随着矩阵的维数增加,松弛阶数和引入的不等式约束的个数会进一步增加;但是也有特例,如例3,这是因为在使用矩阵型方法求解线性矩阵不等式半定互补问题时,有两个子问题在最低阶松弛阶数时不收敛,所以需要求解更高阶数的半定问题。因为求解半定问题占据了大量的计算量,所以在例3中方法2的计算时间大于方法1;
2) 一般情况下,随着矩阵维数的增加,用标量型方法和矩阵型方法求解时的消耗时间的差别会更大,这是因为当用标量型松弛方法求解时,松弛阶数和引入的不等式约束的数量会随着矩阵的维数的增加而快速增加。所以,在一般情况下,当矩阵维数较大时,使用矩阵型方法更有优势。
6. 结语
线性矩阵不等式半定互补问题是一种新型的半定互补问题,是半定规划问题与互补问题的交叉研究内容。该问题的求解可以转化为一系列带有线性矩阵不等式约束的多项式优化子问题,进而可以采用标量型松弛方法或矩阵型松弛方法进行求解。当这个问题的实数解个数有限时,利用本文给出的算法4.3.1或4.3.2可以求出线性矩阵不等式半定互补问题的全部实数解。在数值实验部分,将算法4.3.1和4.3.2进行了比较,验证了这两类算法都可以对线性矩阵不等式半定互补问题进行求解,但在一般情况下,当矩阵的维数较大时,矩阵型算法更有优势。此外,我们还可以考虑利用本文给出的算法4.3.1和4.3.2求解更加一般的问题。例如,给定 ,寻求解 满足 , , , ,其中 是线性矩阵不等式。另外,我们也可以考虑采用算法4.3.1和算法4.3.2求解问题: , , ,其中 是多项式矩阵不等式。
基金项目
中央高校基本科研业务费专项资金资助项目(19D110905)。
文章引用
孔汕汕,赵 馨. 线性矩阵不等式半定互补问题的数值求解方法
Numerical Methods for the Semidefinite Complementarity Problem with Linear Matrix Inequalities[J]. 理论数学, 2022, 12(01): 183-196. https://doi.org/10.12677/PM.2022.121023
参考文献
- 1. 戴昊, 崔志文, 袁鹏, 等. 基于线性矩阵不等式的巡检机器人路径规划[J]. 机械制造与自动化, 2021, 50(4): 212-215.
- 2. Park, I.S., Park, C., Kwon, N.K., et al. (2021) Dynamic Output-Feedback Control for Singular Inter-val-Valued Fuzzy Systems: Linear Matrix Inequality Approach. Information Sciences, 576, 393-406. https://doi.org/10.1016/j.ins.2021.06.053
- 3. Lasserre, J.B. (2001) Global Optimization with Polynomials and the Problem of Moments. SIAM Journal on Optimization, 11, 796-817. https://doi.org/10.1137/S1052623400366802
- 4. Hol, C.W.J. and Scherer, C.W. (2004) Sum of Squares Relaxa-tions for Polynomial Semi-Definite Programming. Proceedings Symposium on Mathematical Theory of Networks and Systems (MTNS), Leuven, 5-9 July 2004.
- 5. Hol, C.W.J. and Scherer, C.W. (2005) A Sum-of-Squares Approach to Fixed-Order -Synthesis. In: Positive Polynomials in Control, Springer, Berlin, 45-71. https://doi.org/10.1007/10997703_3
- 6. Kojima, M. (2003) Sums of Squares Relaxations of Polynomial Semi-Definite Programs. Institute of Technology.
- 7. Henrion, D. and Lasserre, J.B. (2006) Convergent Relaxations of Polynomial Matrix Inequalities and Static Output Feedback. IEEE Transactions on Automatic Control, 51, 192-202. https://doi.org/10.1109/TAC.2005.863494
- 8. Nie, J.W. (2015) The Hierarchy of Local Minimums in Polynomial Optimization. Mathematical Programming, 151, 555-583. https://doi.org/10.1007/s10107-014-0845-2
- 9. 张怡, 阎晓艳. 用线性矩阵不等式方法求解控制理论问题[J]. 机械管理开发, 2006, 28(1): 24-25.
- 10. Nesterov, Y. and Nemirovskii, A. (1994) Interior-Point Polynomial Algorithms in Convex Programming. Society for Industrial and Applied Mathematics, Philadelphia. https://doi.org/10.1137/1.9781611970791
- 11. 王萼芳, 石生明. 高等代数[M]. 第四版. 北京: 高等教育出版社, 2013.
- 12. Griva, I., Shanno, D.F., Vanderbei, R.J., et al. (2008) Global Convergence of a Primal-Dual Interior-Point Method for Nonlinear Programming. Algorithmic Operations Research, 3, 12-29.
- 13. Löfberg, J. (2004) YALMIP: A Toolbox for Modeling and Optimization in MATLAB. 2004 IEEE Inter-national Conference on Robotics and Automation, Taipei, 2-4 September 2004, 284-289. https://doi.org/10.1109/CACSD.2004.1393890
- 14. Sturm, J.F. (1999) Using SeDuMi 1.02, a MATLAB Toolbox for Optimization over Symmetric Cones. Optimization Methods and Software, 11, 625-653. https://doi.org/10.1080/10556789908805766
- 15. Henrion, D., Lasserre, J.B. and Löfberg, J. (2009) Gloptipoly3: Moments, Optimization and Semi-Definite Programming. Optimization Methods and Software, 24, 761-779. https://doi.org/10.1080/10556780802699201
NOTES
*通讯作者。
