设为首页 加入收藏 期刊导航 网站地图

Advances in Applied Mathematics
Vol. 08  No. 12 ( 2019 ), Article ID: 33653 , 12 pages
10.12677/AAM.2019.812240

The Numerical Analysis and Simulation Based on A Mixed Finite Element Method for the MRLW Equation

Enyu Fan

School of Mathematical Sciences, Inner Mongolia University, Hohhot Inner Mongolia

Received: Dec. 2nd, 2019; accepted: Dec. 19th, 2019; published: Dec. 26th, 2019

ABSTRACT

A second-order backward-difference mixed finite element (MFE) method for modified regularized long wave (MRLW) equation is proposed and discussed in this paper. The spatial direction is approximated by the mixed Galerkin method using mixed linear space finite elements, and the time direction is considered by backward difference scheme with second-order convergence rate. The optimal error estimates for u in L2 and H1-norms and its flux q = ux and in L2-norm are derived. Some numerical results are given to test our theoretical analysis and illustrate the efficiency of the studied method.

Keywords:MRLW Equation, Second-Order Backward Difference Method, Mixed Finite Element Method, Optimal Error Estimates, Numerical Simulation

修正RLW方程的一种混合有限元方法的 数值分析与模拟

樊恩宇

内蒙古大学数学科学学院，内蒙古 呼和浩特

收稿日期：2019年12月2日；录用日期：2019年12月19日；发布日期：2019年12月26日

摘 要

本文针对修正的RLW方程提出并讨论了一种二阶向后差分的混合有限元方法。在空间方向上使用混合Galerkin有限元方法来近似，在时间上采用向后差分二阶离散格式来近似。并且得到了方程的未知解u在L2模和H1模下的最优误差估计以及 q = u x 在L2模下的最优误差估计。为了对数值理论进行有效性验证，我们通过一些数值算例给出一些数值模拟结果。

关键词 :修正RLW方程，二阶向后差分方法，混合有限元方法，最优误差估计，数值模拟

Copyright © 2019 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

本文考虑带有初边值条件的修正RLW方程问题：

{ u t + u x + 6 u 2 u x − μ u x x t = 0 ,   ( x , t ) ∈ I × J u ( a , t ) = u ( b , t ) = 0 ,   t ∈ J ¯ , u ( x , 0 ) = u 0 ( x ) ,   x ∈ I ¯ , (1.1)

其中 I = ( a , b ) ， J = [ 0 , T ] ( 0 < T < ∞ ) 。初始函数 u 0 ( x ) 为已知函数，系数 μ 为正常数。

近几年来，物理、生物、流体力学等研究领域均出现了很多的非线性现象，而这些现象都可以由一些非线性发展方程的数学模型来描述。特别地是，越来越多的学者将关注点放在了非线性色散波研究领域中较为重要的非线性RLW方程中 [1]。孤立波在非线性分散介质中是波包或脉冲，由于非线性和色散影响之间的动态平衡，这些波的波形会保持不变，而孤波是一种非常特殊的类型，在与其他波进行碰撞后波形依然保持不变。RLW方程对于更为一般的KdV方程是一种非线性分散波的替代描述。我们考虑文献 [1] - [23] 中的数学理论以及数值方法。文献 [5] 中讨论了RLW方程解的存在性和唯一性，因为只有在有限的初边值条件下方程才有解析解，因此他们将焦点放在了数值的角度。在一些文献中已经有很多针对RLW方程的数值方法，比如差分方法 [5] [6] [15]，基于Galerkin和排列原则的有限元方法 [7] [8] [9] [10] [11]，混合有限元方法 [12] [13] [14] [23]，无网格法 [16] 等。

Mei和Chen [18] 针对RLW方程研究了基于Galerkin方法的显式两步方法。在本文中，我们的目的是对修正RLW方程研究一种显式两步混合元法，利用混合Galerkin方法逼近空间方向，向后二阶差分格式逼近时间方向。我们在全离散显式两步混合格式下，得到了未知函数u在 L 2 模和 H 1 模下最优误差估计和其辅助变量 q = u x 基于 L 2 模最优误差估计，并与其他的数值方法的准确性进行了比较。通过与文献 [18] [24] [25] 中的数值方法进行比较，我们得到了u与 q = u x 的近似值。

文章的整体结构如下所示，第二部分中，给出了一个显式多步混合方法以及数值过程。第三部分中，证明了u与 q = u x 分别在 L 2 模和 H 1 模下基于二阶向后差分混合方法的最优误差估计。第四部分中，给出一些数值算例，对理论的结果进行数值验证，最后对整篇论文做了总结。在整篇文章中，C表示一般的正常数，与剖分步长h与 Δ t 无关。

2. 混合有限元数值方法

引入辅助变量 q = u x ，我们可以将方程(1.1)整理为如下形式：

u x = q (2.1)

u t + q + 6 u 2 q − μ q x t = 0. (2.2)

要得到方程(2.1)~(2.2)的混合弱形式，也就是找到 { u , q } : [ 0 , T ] ↦ H 0 1 ∗ L 2 ( Ω ) 使得如下系统成立：

( u x , w ) = ( q , w ) , ∀ w ∈ L 2 ( Ω ) (2.3)

( u t , v ) + ( q , v ) + 6 ( u 2 q , v ) + μ ( q t , v x ) = 0 , ∀ v ∈ H 0 1 .(2.4)

使 V h 与 W h 分别为 H 0 1 和 L 2 ( Ω ) 的有限维子空间，其定义如下：

V h = { v h | v h ∈ C 0 ( I ¯ ) , v h | I j ∈ P k ( I j ) , ∀ I j ∈ T h , v h ( a ) = v h ( b ) = 0 } ⊂ H 0 1 ,

W h = { w h | w h ∈ L 2 ( Ω ) , w h | I j ∈ P r ( I j ) , ∀ I j ∈ T h } ⊂ L 2 ( Ω ) ,

其中 T h 为小区间的集合，即将 I ¯ = [ a , b ] 剖分为N个子区间，分别为 I j = [ x j , x j + 1 ] ， j = 0 , 1 , 2 , ⋯ , ( N − 1 ) ， h j = x j + 1 − x j ， h = max 0 ≤ j ≤ N − 1 h j ， P m ( I j ) 表示在 I j 中小于等于m的多项式。方程(2.3)和(2.4)的半离散混合有限元方法就是找到 { u h , q h } : [ 0 , T ] ↦ V h × W h ，使得：

( u h x , w h ) = ( q h , w h ) ,     ∀ w h ∈ W h , (2.5)

( u h t , v h ) + ( q h , v h ) + 6 ( ( u h ) 2 q h , v h ) + μ ( q h t , v h x ) = 0 ,     ∀ v h ∈ V h . (2.6)

3. 二阶向后差分混合方法和最优误差估计

3.1. 二阶向后差分方法和相关定理

在这部分，我们将对修正的RLW方程在二阶向后差分混合有限元下讨论先验误差估计。对于整个离散过程，我们对时间区间 [ 0 , T ] 进行剖分， 0 < t 0 < t 1 < ⋯ < t N = T ，其中步长为 Δ t = T / N ，N为正整数。 ϕ 为 [ 0 , T ] 上的光滑函数，定义 ϕ n = ϕ ( t n ) ，以及 ∂ t 2 u n + 1 = 3 u n + 1 − 4 u n + u n − 1 2 Δ t 。在时间 t = t n + 1 处，方程(2.3)-(2.4)有如下形式；

( u x n + 1 , w ) = ( q n + 1 , w ) ,   ∀ w ∈ L 2 ( Ω ) , (3.1)

( u t n + 1 , v ) + ( q n + 1 , v ) + 6 ( ( u n + 1 ) 2 q n + 1 , v ) + μ ( q t n + 1 , v x ) = 0 ,   ∀ v ∈ H 0 1 . (3.2)

将方程(3.1)~(3.2)在时间方向上利用向后二阶差分近似，我们得到线性化的时间离散形式：

( u x n + 1 , w ) = ( q n + 1 , w ) ,   ∀ w ∈ L 2 ( I ) , (3.3)

( ∂ t 2 u n + 1 , v ) + μ ( ∂ t 2 q n + 1 , v x ) + ( q n + 1 , v ) + 6 ( 2 ( u n ) 2 q n − ( u n − 1 ) 2 q n − 1 , v ) = ( τ 1 n + 1 , v ) + ( τ 2 n + 1 , v x ) + 6 ( τ 3 n + 1 , v ) ,   ∀ v ∈ H 0 1 , (3.4)

其中

τ 1 n + 1 = ∂ t 2 u n + 1 − u t n + 1 , τ 2 n + 1 = μ ( ∂ t 2 q x n + 1 − q x t n + 1 ) , τ 3 n + 1 = ( 2 ( u n ) 2 q n − ( u n − 1 ) 2 q n − 1 ) − ( u n + 1 ) 2 q n + 1 . (3.5)

引理3.1：(文献 [26] )对于 τ i n + 1 , i = 1 , 2 , 3 ，下列估计成立：

‖ τ 1 n + 1 ‖ + ‖ τ 2 n + 1 ‖ + ‖ τ 3 n + 1 ‖ ≤ C Δ t 2 . (3.6)

引理3.2：(文献 [26] )对于数列 { w n } ，下列不等式成立：

( ∂ t 2 w n + 1 , w n + 1 ) ≥ 1 4 Δ t [ ‖ w n + 1 ‖ 2 + ‖ 2 w n + 1 − w n ‖ 2 − ‖ w n ‖ 2 − ‖ 2 w n − w n − 1 ‖ 2 ] . (3.7)

现在我们需要在 V h × W h 中找到一组 { u h n + 1 , q h n + 1 } 满足：

( u h x n + 1 , w h ) = ( q h n + 1 , w h ) ,   ∀ w h ∈ W h , (3.8)

和

( ∂ t 2 u h n + 1 , v h ) + μ ( ∂ t 2 q h n + 1 , v h x ) + ( q h n + 1 , v h ) + 6 ( 2 ( u h n ) 2 q h n − ( u h n − 1 ) 2 q h n − 1 , v h ) = 0 ,   ∀ v h ∈ V h . (3.9)

为了先验误差估计的理论分析，针对我们的方程引入了一些投影。

引理3.3：(文献 [12] [17] [27] )若存在一个非线性算子 Π h : L 2 ( Ω ) → W h 使得下式成立

( q − Π h q , v h x ) = 0 ,   v h ∈ V h , (3.10)

则下面的估计式成立：

‖ q − Π h q ‖ ≤ C h k + 1 ‖ q ‖ k + 1 , (3.11)

引理3.4：(文献 [12] [17] [27] )对于任意的 u ∈ H 0 1 成立

( u x − P h u x , w h ) = 0 ,   w h ∈ W h , (3.12)

则有

‖ u x − P h u x ‖ + h ‖ u − P h u ‖ 1 ≤ C h k + 1 ‖ u ‖ k + 1 (3.13)

为了全离散误差估计，我们将误差可以写为：

u n − u h n = ( u n − P h u n ) + ( P h u n − u h n ) = η n + ς n ,

q n − q h n = ( q n − Π h q n ) + ( Π h q n − q h n ) = ρ n + ξ n .

联立方程(3.10)，(3.13)，(3.3)，(3.4)，(3.8)和(3.9)，在 t = t n + 1 处可以得到如下的误差方程：

( ξ n + 1 + ρ n + 1 , w h ) = ( ς x n + 1 , w h ) ,   ∀ w h ∈ W h , (3.14)

( ∂ t 2 ς n + 1 , v h ) + μ ( ∂ t 2 ξ n + 1 , v h x ) + 6 ( 2 ( ( u n ) 2 q n − ( u h n ) 2 q h n ) − ( ( u n − 1 ) 2 q n − 1 − ( u h n − 1 ) 2 q h n − 1 ) , v h ) + ( ρ n + 1 + ξ n + 1 , v h ) = − ( ∂ t 2 η n + 1 , v h ) + ( τ 1 n + 1 , v h ) + ( τ 2 n + 1 , v h x ) + 6 ( τ 3 n + 1 , v h ) ,   v h ∈ V h . (3.15)

3.2. 最优误差估计

这部分中将得到全离散最优误差估计，并且获得了如下的定理3.5

定理3.5：已知 u h 0 ∈ V h ,   q h 0 ∈ W h ，则

‖ u n − u h n ‖ + ‖ q n − q h n ‖ ≤ C ( h k + 1 + Δ t 2 ) , ‖ u n − u h n ‖ 1 ≤ C ( h k + Δ t 2 ) .

证明：由(3.14)可得

( ∂ t 2 ξ n + 1 , w h ) = ( ∂ t 2 ς x n + 1 , w h ) − ( ∂ t 2 ρ n + 1 , w h ) ,   ∀ w h ∈ W h , (3.16)

在(3.15)和(3.16)中分别令 v h = ς n + 1 ， w h = μ ς x n + 1 ，可以得到下面方程

( ∂ t 2 ς n + 1 , ς n + 1 ) + μ ( ∂ t 2 ς x n + 1 , ς x n + 1 ) = μ ( ∂ t 2 ρ n + 1 , ς x n + 1 ) − 6 ( 2 ( ( u n ) 2 q n − ( u h n ) 2 q h n ) − ( ( u n − 1 ) 2 q n − 1 − ( u h n − 1 ) 2 q h n − 1 ) , ς n + 1 )   + ( ρ n + 1 + ξ n + 1 , ς n + 1 ) + ( τ 1 n + 1 , ς n + 1 ) + ( τ 2 n + 1 , ς x n + 1 ) + 6 ( τ 3 n + 1 , ς n + 1 ) ≤ C ( ‖ 2 ( ( u n ) 2 q n − ( u h n ) 2 q h n ) − ( ( u n − 1 ) 2 q n − 1 − ( u h n − 1 ) 2 q h n − 1 ) ‖ 2         + ‖ ρ n + 1 ‖ 2 + ‖ ξ n + 1 ‖ 2 + ‖ τ 1 n + 1 ‖ 2 + ‖ τ 2 n + 1 ‖ 2 + ‖ τ 3 n + 1 ‖ 2 + ‖ ς n + 1 ‖ 2 + ‖ ς x n + 1 ‖ 2 ) . (3.17)

现在我们估计不等式可以得到

‖ 2 ( ( u n ) 2 q n − ( u h n ) 2 q h n ) − ( ( u n − 1 ) 2 q n − 1 − ( u h n − 1 ) 2 q h n − 1 ) ‖ 2 ≤ ‖ 2 ( u n ) 2 ( q n − q h n ) + 2 ( ( u n ) 2 − ( u h n ) 2 ) q h n − ( ( u n − 1 ) 2 ( q n − 1 − q h n − 1 ) + [ ( u n − 1 ) 2 − ( u h n − 1 ) 2 ] q h n − 1 ) ‖ 2 ≤ C ∑ j = n − 1 n [ ‖ ( u j ) 2 ‖ ∞ 2 ( ‖ ξ j ‖ + ‖ ρ j ‖ ) 2 + ( ‖ u j ‖ ∞ + ‖ u h j ‖ ∞ ) 2 ‖ q h j ‖ ∞ 2 ( ‖ η j ‖ + ‖ ς j ‖ ) 2 ] ≤ C ( ‖ ρ n ‖ 2 + ‖ ρ n − 1 ‖ 2 + ‖ η n ‖ 2 + ‖ η n − 1 ‖ 2 + ‖ ξ n ‖ 2 + ‖ ξ n − 1 ‖ 2 + ‖ ς n ‖ 2 + ‖ ς n − 1 ‖ 2 ) . (3.18)

在方程(3.14)中，我们令 w h = ξ n + 1 ，使用Cauchy-Schwarz不等式可以得到

‖ ξ n + 1 ‖ 2 ≤ C ( ‖ ρ n + 1 ‖ 2 + ‖ ς x n + 1 ‖ 2 ) . (3.19)

现在联合方程(3.17)，(3.18)，(3.19)可以得到

( ∂ t 2 ς n + 1 , ς n + 1 ) + μ ( ∂ t 2 ς x n + 1 , ς x n + 1 ) = μ ( ∂ t 2 ρ n + 1 , ς x n + 1 ) − 6 ( 2 ( ( u n ) 2 q n − ( u h n ) 2 q h n ) − ( ( u n − 1 ) 2 q n − 1 − ( u h n − 1 ) 2 q h n − 1 ) , ς n + 1 )   + ( ρ n + 1 + ξ n + 1 , ς n + 1 ) + ( τ 1 n + 1 , ς n + 1 ) + ( τ 2 n + 1 , ς x n + 1 ) + 6 ( τ 3 n + 1 , ς n + 1 ) ≤ C ( ‖ ρ n + 1 ‖ 2 + ‖ τ 1 n + 1 ‖ 2 + ‖ τ 2 n + 1 ‖ 2 + ‖ τ 3 n + 1 ‖ 2 + ∑ i = n − 1 n + 1 ( ‖ ς i ‖ 2 + ‖ ς x i ‖ 2 )         + ‖ ∂ t 2 ρ n + 1 ‖ 2 + ‖ ρ n ‖ 2 + ‖ ρ n − 1 ‖ 2 + ‖ η n ‖ 2 + ‖ η n − 1 ‖ 2 ) . (3.20)

利用引理3.2，并且用 4 Δ t 乘方程(3.20)，我们得到

‖ ς n + 1 ‖ 1 2 + ‖ 2 ς n + 1 − ς n ‖ 1 2 − ‖ ς n ‖ 1 2 − ‖ 2 ς n − ς n − 1 ‖ 1 2 ≤ C ( ‖ ρ n + 1 ‖ 2 + ‖ τ 1 n + 1 ‖ 2 + ‖ τ 2 n + 1 ‖ 2 + ‖ τ 3 n + 1 ‖ 2 + ∑ i = n − 1 n + 1 ( ‖ ς i ‖ 2 + ‖ ς x i ‖ 2 ) + ‖ ∂ t 2 ρ n + 1 ‖ 2 + ‖ ρ n ‖ 2 + ‖ ρ n − 1 ‖ 2 + ‖ η n ‖ 2 + ‖ η n − 1 ‖ 2 ) . (3.21)

对n求和并使用离散Gronwall引理，可以得到：

‖ ς n + 1 ‖ 1 2 + ‖ 2 ς n + 1 − ς n ‖ 1 2 − ‖ ς n ‖ 1 2 − ‖ 2 ς n − ς n − 1 ‖ 1 2 ≤ C ( ‖ ρ n + 1 ‖ 2 + ‖ τ 1 n + 1 ‖ 2 + ‖ τ 2 n + 1 ‖ 2 + ‖ τ 3 n + 1 ‖ 2     + ‖ ∂ t 2 ρ n + 1 ‖ 2 + ‖ ρ n ‖ 2 + ‖ ρ n − 1 ‖ 2 + ‖ η n ‖ 2 + ‖ η n − 1 ‖ 2 ) . (3.22)

联立方程(3.20)和(3.19)可以得到

‖ ξ n + 1 ‖ 2 ≤ C ( ‖ ρ n + 1 ‖ 2 + ‖ τ 1 n + 1 ‖ 2 + ‖ τ 2 n + 1 ‖ 2 + ‖ τ 3 n + 1 ‖ 2     + ‖ ∂ t 2 ρ n + 1 ‖ 2 + ‖ ρ n ‖ 2 + ‖ ρ n − 1 ‖ 2 + ‖ η n ‖ 2 + ‖ η n − 1 ‖ 2 ) . (3.23)

联立方程(3.22)~(3.23)，引理3.3~3.4以及三角不等式可以得到定理中的结论。

4. 数值实验

在这部分中，为了检验显式两步方法的有效性和准确性，我们给出了不同时间层上单波传播以及双波碰撞数值算例。为了检验数值格式的守恒，我们可以考虑如下三个不变量：

I 1 = ∫ a b u d x ≈ h ∑ j = 1 N u j n , I 2 = ∫ a b ( u 2 + μ ( u x ) 2 ) d x ≈ h ∑ j = 1 N [ ( u j n ) 2 + μ [ ( u x ) j n ] 2 ]   , I 3 = ∫ a b ( u 4 − μ ( u x ) 2 ) d x ≈ h ∑ j = 1 N [ ( u j n ) 4 − μ [ ( u x ) j n ] 2 ]   .

其中 I 1 , I 2 , I 3 通常被称为质量，动量和能量。

我们考虑MRLW方程(1.1)，其单波解为

u ( x , t ) = c   sech ( p ( x − ( c + 1 ) t − x 0 ) ) (4.1)

其中 p = c μ ( 1 + c ) ， x 0 和c是任意的常数。变量的解析值为

I 1 = π c p , I 2 = 2 c p + 2 μ p c 3 , I 3 = 4 c 2 3 p − 2 μ p c 3 .

我们讨论单孤立波的运动，并且令初始条件为

u ( x , 0 ) = c   sech ( p ( x − x 0 ) ) (4.2)

其中 c = 1 , x 0 = 20 。在整个过程中，我们令 0 ≤ x ≤ 100 , 0 ≤ t ≤ 10 。

表1中，令空间剖分的步长为 h = 0.125 ，时间剖分的步长为 Δ t = 0.0125 ，表中列出了三个不变量 I 1 , I 2 , I 3 在不同时间 t = 2 ,   4 ,   6 ,   8 ,   10 的具体数值。从表中的结果可以看出我们的方法对不变量保持的是比较好的。

表2中，令空间剖分步长固定为 h = 0.125 ，得到了u在不同时间层 t = 2 ,   4 ,   6 ,   8 ,   10 上，时间剖分步长为 Δ t = 0.025 ,   0.05 ,   0.1 时，在 L 2 模下的最优误差结果。从表2中我们容易看到时间的收敛阶为2。同理，q的相关结果在表3中体现。

表4中，我们固定时间剖分步长为 Δ t = 0.01 ，得到了u在不同时间层 t = 2 ,   4 ,   6 ,   8 ,   10 上，空间剖分步长为 h = 0.2 ,   0.4 ,   0.8 下的 L 2 模最优误差结果。从表中易知，在空间方向上的收敛阶为2。同理，q的相关结果在表5中体现。

Table 1. Invariants of single solitary wave. h = 0 , 125 , Δ t = 0.0125 , c 1 = 1 , c 2 = 0.5

表1. 孤立波的不变量。 h = 0 , 125 , Δ t = 0.0125 , c 1 = 1 , c 2 = 0.5

Table 2. Convergence order and error in L2-norm for u of time. h = 0.125 , c = 1

表2. u的L2误差和时间收敛阶。 h = 0.125 , c = 1

Table 3. Convergence order and error in L2-norm for q of time. h = 0. 125 , c = 1

表3. q的L2误差和时间收敛阶。 h = 0. 125 , c = 1

Table 4. Convergence order and error in L2-norm for u of space. Δ t = 0.01 , c = 1

表4. u的L2误差和空间收敛阶。 Δ t = 0.01 , c = 1

Table 5. Convergence order and error in L2-norm for q of space. Δ t = 0.01 , c = 1

表5. q的L2误差和空间收敛阶。 Δ t = 0.01 , c = 1

Figure 1. Surface for exact solution u

图1. 精确解u

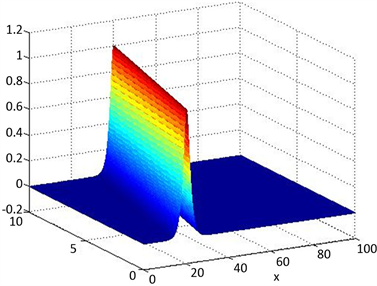
Figure 2. Surface for numerical solution uh

图2. 数值解uh

图1为精确解u在 ( x , t ) ∈ [ 0 , 100 ] × [ 0 , 10 ] 下的三维图像，图2为 h = 0.2 , Δ t = 0.02 时，数值解uh的三维图像。从图1和图2可以看出，数值解uh很好的近似了精确解u。图3和图4分别为q的精确值与 h = 0.2 , Δ t = 0.02 下的数值解qh的三维对比图，我们可以看出数值解qh很好的近似了精确解q。

Figure 3. Surface for exact solution q

图3. 精确解q

Figure 4. Surface for numerical solution qh

图4. 数值解qh

Figure 5. Comparison between u and uh

图5. u和uh对比图

Figure 6. Comparison between q and qh

图6. q和qh对比图

Figure 7. Numerical solution uh

图7. 数值解uh

Figure 8. Numerical solution qh

图8. 数值解qh

图5表示在 h = 0.2 , Δ t = 0.02 时，不同时间层 t = 2 ,   4 ,   6 ,   8 ,   10 上数值解uh和精确值u的对比图。同理，图6为q的相关对比图。图5和图6表示的单孤立波朝右运动时u和q保持波形和速度不变。可以看出数值解uh和qh可以很好的近似精确值u和q。

图7和图8表示的是单孤立波在不同时间层 t = 2 ,   4 ,   6 ,   8 ,   10 的三维线图。

从上述表1~5和图1~8的分析，我们知道数值结果与定理3.6中的理论结果是比较吻合的，并且也验证了的我们的方法对于MRLW方程的有效性。

5. 结论

所本文中，我们对于MRLW方程提出并分析了一种显式二阶向后差分的混合有限元方法，即在空间方向上利用混合有限元方法，在时间方向上使用二阶向后差分方法。我们讨论了方法的数值过程，对该方法的全离散格式证明了相关的理论结果，并且与其他数值相比较，我们获得了很好的误差收敛阶。从数值算例的结果可以看到，我们的方法对于MRLW方程是比较有效的。

基金项目

本文由内蒙古自然科学基金项目(2016MS0102)资助。

文章引用

樊恩宇. 修正RLW方程的一种混合有限元方法的数值分析与模拟
The Numerical Analysis and Simulation Based on A Mixed Finite Element Method for the MRLW Equation[J]. 应用数学进展, 2019, 08(12): 2096-2107. https://doi.org/10.12677/AAM.2019.812240

参考文献

  1. 1. Shi, D.Y. and Yang, H. (2016) A New Approach of Superconvergence Analysis for Nonlinear BBM Equation on Anisotropic Meshes. Applied Mathematics Letters, 58, 74-80.
    https://doi.org/10.1016/j.aml.2016.02.007

  2. 2. Benjamin, T.B., Bona, J.L. and Mahony, J.J. (1972) Model Equations for Long Waves in Nonlinear Dispersive Systems. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 272, 47-78.
    https://doi.org/10.1098/rsta.1972.0032

  3. 3. Olver, P.J. (1979) Euler Operators and Conservation Laws of the BBM Equation. Mathematical Proceedings of the Cambridge Philosophical Society, 85, 143-160.
    https://doi.org/10.1017/S0305004100055572

  4. 4. Saka, B., Şahin, A. and Dağ, İ. (2011) B-Spline Collocation Algorithms for Numerical Solution of the RLW Equation. Numerical Methods for Partial Differential Equations, 27, 581-607.
    https://doi.org/10.1002/num.20540

  5. 5. Bona, J.L. and Bryant, P.J. (1973) A Mathematical Model for Long Waves Generated by Wavemakers in Non-Linear Dispersive Systems. Mathematical Proceedings of the Cambridge Philosophical Society, 73, 391-405.
    https://doi.org/10.1017/S0305004100076945

  6. 6. Zhang, L. (2005) A Finite Difference Scheme for Generalized Regularized Long-Wave Equation. Applied Mathematics and Computation, 168, 962-972.
    https://doi.org/10.1016/j.amc.2004.09.027

  7. 7. Dagˇ, İ., DoĞan, A. and Saka, B. (2003) B-Spline Collocation Methods for Numerical Solutions of the RLW Equation. International Journal of Computer Mathematics, 80, 743-757.
    https://doi.org/10.1080/0020716021000038965

  8. 8. Esen, A. and Kutluay, S. (2006) Application of a Lumped Galerkin Method to the Regularized Long Wave Equation. Applied Mathematics and Computation, 174, 833-845.
    https://doi.org/10.1016/j.amc.2005.05.032

  9. 9. Dağ, İ., Saka, B. and Irk, D. (2006) Galerkin Method for the Numerical Solution of the RLW Equation Using Quintic B-Splines. Journal of Computational and Applied Mathematics, 190, 532-547.
    https://doi.org/10.1016/j.cam.2005.04.026

  10. 10. Raslan, K.R. (2005) A Computational Method for the Regularized Long Wave (RLW) Equation. Applied Mathematics and Computation, 167, 1101-1118.
    https://doi.org/10.1016/j.amc.2004.06.130

  11. 11. Wahlbin, L. (1974) Error Estimates for a Galerkin Method for a Class of Model Equations for Long Waves. Numerische Mathematik, 23, 289-303.
    https://doi.org/10.1007/BF01438256

  12. 12. Luo, Z. and Liu, R. (1998) Mixed Finite Element Analysis and Numerical Solitary Solution for the RLW Equation. SIAM Journal on Numerical Analysis, 36, 89-104.
    https://doi.org/10.1137/S0036142996312999

  13. 13. Guo, L. and Chen, H. (2006) H1-Galerkin Mixed Finite Element Method for the Regularized Long Wave Equation. Computing, 77, 205-221.
    https://doi.org/10.1007/s00607-005-0158-7

  14. 14. Gu, H. and Chen, N. (2008) Least-Squares Mixed Finite Element Methods for the RLW Equations. Numerical Methods for Partial Differential Equations: An International Journal, 24, 749-758.
    https://doi.org/10.1002/num.20285

  15. 15. Bona, J.L., Pritchard, W.G. and Scott, L.R. (1985) Numerical Schemes for a Model for Nonlinear Dispersive Waves. Journal of Computational Physics, 60, 167-186.
    https://doi.org/10.1016/0021-9991(85)90001-4

  16. 16. Haq, S. and Ali, A. (2009) A Meshfree Method for the Numerical Solution of the RLW Equation. Journal of Computational and Applied Mathematics, 223, 997-1012.
    https://doi.org/10.1016/j.cam.2008.03.039

  17. 17. 陈邵春, 陈红如. 二阶椭圆问题新的混合元格式[J]. 计算数学, 2010, 32(2): 213-218.

  18. 18. Mei, L. and Chen, Y. (2012) Explicit Multistep Method for the Numerical Solution of RLW Equation. Applied Mathematics and Computation, 218, 9547-9554.
    https://doi.org/10.1016/j.amc.2012.03.050

  19. 19. Gardner, L.R.T., Gardner, G.A. and Dogan, A. (1996) A Least-Squares Finite Element Scheme for the RLW Equation. Communications in Numerical Methods in Engineering, 12, 795-804.
    https://doi.org/10.1002/(SICI)1099-0887(199611)12:11<795::AID-CNM22>3.0.CO;2-O

  20. 20. Daǧ, İ. (2000) Least-Squares Quadratic B-Spline Finite Element Method for the Regularised Long Wave Equation. Computer Methods in Applied Mechanics and Engineering, 182, 205-215.
    https://doi.org/10.1016/S0045-7825(99)00106-1

  21. 21. Daǧ, İ. and Özer, M.N. (2001) Approximation of the RLW Equation by the Least Square Cubic B-Spline Finite Element Method. Applied Mathematical Modelling, 25, 221-231.
    https://doi.org/10.1016/S0307-904X(00)00030-5

  22. 22. Dogan, A. (2002) Numerical Solution of RLW Equation Using Linear Finite Elements within Galerkin’s Method. Applied Mathematical Modelling, 26, 771-783.
    https://doi.org/10.1016/S0307-904X(01)00084-1

  23. 23. 刘洋, 李宏. 偏微分方程的非标准混合有限元方法[M]. 北京: 国防工业出版社, 2015.

  24. 24. Chatzipantelidis, P. (1998) Explicit Multistep Methods for Nonstiff Partial Differential Equations. Applied Numerical Mathematics, 27, 13-31.
    https://doi.org/10.1016/S0168-9274(97)00112-8

  25. 25. Akrivis, G., Karakashian, O. and Karakatsani, F. (2003) Linearly Implicit Methods for Nonlinear Evolution Equations. Numerische Mathematik, 94, 403-418.
    https://doi.org/10.1007/s00211-002-0432-y

  26. 26. Liu, Y., Li, H., Du, Y. and Wang, J. (2013) Explicit Multistep Mixed Finite Element Method for RLW Equation. Abstract and Applied Analysis, 2013, Article ID: 768976.
    https://doi.org/10.1155/2013/768976

  27. 27. Liu, Y., Li, H., Gao, W., He, S. and Fang, Z. (2014) A New Mixed Element Method for a Class of Time-Fractional Partial Differential Equations. The Scientific World Journal, 2014, Article ID: 141467.
    https://doi.org/10.1155/2014/141467

期刊菜单