Journal of Oil and Gas Technology
Vol.39 No.06(2017), Article ID:23060,12
pages
10.12677/JOGT.2017.396100
The Calculation of Circulating Pressure Loss in Coiled-tubing Drilling
Yuanzhu Mi, Yue Luo, Zhiming Huang
School of Chemistry & Environmental Engineering, Yangtze University, Jingzhou Hubei

Received: Oct. 30th, 2017; accepted: Nov. 7th, 2017; published: Dec. 15th, 2017



ABSTRACT
A block of Liaohe Oilfield was taken as research object, based on geological condition of the block and performance parameter of coiled-tubing drilling rig, the pressure loss of different sections was calculated in coiled-tubing drilling(CT) including pressure loss of CT twisting in reel, downhole CT, annulus and total circulating. Especially, the effect of some important factors on total circulating pressure loss was discussed such as flow rate Q, consistency index K and rheological index n. Rheological properties parameter for coiled drilling fluid was determined by combining calculation results and practical experience. The calculation results show that it was desirable that Q is selected at 0.01 m3/s, n is at 0.4-0.5 and K is at 0.7-1.0 Pa∙sn in the water-based solid-free drilling fluid. Certain theoretical basis is provided for the design of fluids used in coiled-tubing drilling.
Keywords:Coiled-tubing Drilling, Water-based Drilling Fluid, Circulating Pressure Loss, Rheological Property Parameter
连续管钻井循环压耗的计算
米远祝,罗跃,黄志明
长江大学化学与环境工程学院,湖北 荆州
作者简介:米远祝(1972-),男,博士,教授,现从事油气井工作液方面的研究。
收稿日期:2017年10月30日;录用日期:2017年11月7日;发布日期:2017年12月15日

摘 要
以辽河油田某区块作为研究对象,以该区块的地质情况、连续管钻机的性能参数等作为计算依据,对连续管钻井中各段压耗包括连续管盘管压耗、连续管直管压耗、环空压耗以及总循环压耗进行了相应的计算,重点探讨了钻井液流量Q,稠度系数K以及流性指数n对连续管循环压耗的影响。根据计算结果,结合实践经验,初步确定了连续管钻井液的流变性能参数。理论计算结果表明,对于水基无固相钻井液而言,Q值选择在0.01 m3/s左右, n值选择在0.4~0.5,K值选择在0.7~1.0 Pa∙sn较为合适。这些计算的理论分析可为连续管钻井液的设计提供一定的理论依据。
关键词 :连续管钻井,水基钻井液,循环压耗,流变性能参数

Copyright © 2017 by authors, Yangtze University and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
1. 引言
连续油管钻井(CTD)技术是20世纪90年代初迅速发展起来的一项低成本、高效率的钻井技术。目前连续管钻井已成功应用于老井重钻、加深、侧钻以及小井眼、欠平衡、过平衡和水平井钻井等多种钻井作业项目,并显示出良好的发展前景。在连续管钻井中,由于井眼尺寸小,连续管直径小以及井眼环空较窄,因此均存在着较大的循环压耗。总的循环压耗主要由环空压耗、连续管压耗以及钻头压耗所组成,而连续管压耗又由盘管压耗和直管压耗两部分所组成。关于连续管压耗的计算,已经有不少的研究报道 [1] - [6] 。Medjani等人 [7] 研究了连续管中牛顿型钻井液的压耗计算,Willingham等人 [8] 对牛顿型和非牛顿型钻井液在连续管盘管和垂直管中的压耗进行了探讨。2001年以来,Shah等人 [9] [10] 研究了钻屑对连续管中循环压耗的影响,同时也预测了连续管压裂过程中的压耗。Zhou等人 [11] 利用理论和实验的方法,研究了幂律型流体的循环压耗。然而,这些研究报道中,很少有研究针对连续管总循环压耗以及连续管直管、盘管和环空中的压耗。Hou等人 [12] 在前人研究的基础上,对连续管总循环压耗,连续管直管、盘管以及环空中的压耗进行了分析和计算。
借鉴Hou等人 [12] 的计算公式,分别对连续管老井侧钻水平井直管、盘管,环空以及总循环压耗进行初步计算,探讨了流量Q、稠度系数K以及流性指数n对连续管钻井中各段压耗以及总循环压耗的影响,以确定连续管钻井液设计中最佳的流变性能参数。
2. 连续管钻井循环压耗计算公式
2.1. 连续管直管循环压耗计算公式
雷诺数:
(1)
式中:Re为雷诺数,1;ρ为钻井液密度,kg/m3;d为连续管内径,m;ν为钻井液流速,m/s;n为流性指数,1;K为稠度系数,Pa·sn。
层流时的摩阻系数:
(2)
式中:fC为层流时的摩阻系数,1。
紊流时的摩阻系数:
(3)
(4)
(5)
式中:f W为紊流时的摩阻系数,1。
过渡流时的摩阻系数:
(6)
循环压耗:
(7)
式中:fG为过渡流时的摩阻系数,1;fj为不同流型时的摩阻系数(j = C,W,G),1;Δp为压耗,MPa;L为连续管长度,m。
2.2. 环空中循环压耗的计算公式
雷诺数:
(8)
式中:D2为井眼直径,m;D1为连续管外径,m。
层流时的摩阻系数fHC:
(9)
紊流时的摩阻系数fHW:
(10)
(11)
(12)
过渡流时的摩阻系数fHG:
(13)
(14)
循环压耗:
(15)
2.3. 盘管中循环压耗的计算公式
在连续管盘管中,由于弯曲半径较小,在黏性力及离心力的作用下Dean旋涡变得比较明显,使连续管盘管中的压耗要远远高于连续管直管中的压耗,因此在连续管盘管中用无单位的Dean数来代替直管中的雷诺数 [13] [14] :
(16)
式中:NDn为Dean数,1;r0为连续管盘管外层半径,m;Ri为第i层的曲率半径,m。
层流时的摩阻系数fPC:
(17)
紊流时的摩阻系数fPW:
(18)
(19)
(20)
过渡流时的摩阻系数fPG:
(21)
(22)
循环压耗:
(23)
2.4. 连续管钻井循环压耗计算参数
取辽河油田某区块及拟用连续管钻机的相关资料作为计算参数。
老井深度:2161m;表层套管:ø 0.2445 m × 393 m;油层套管:ø 0.1397 m × 1768 m;井眼尺寸:118 mm;连续管参数(内径 × 壁厚 × 管长):ø 73 mm × 4.8 mm × 3500 m,级别CT 80;滚筒尺寸(底径 × 内宽 × 轮缘):ø 2600 mm × 2450 mm × ø 4200 mm;钻井液流量:0.005~0.0133 m3/s。
3. 连续管钻井循环压耗的计算
3.1. Q值对循环压耗的影响
已知滚筒内宽C为2.45 m,滚筒底径B(筒芯直径)为2.6 m,没有盘管时筒芯半径为1.3 m,每层连续管的排数为33.56 (圆整取33)。
利用上面给定数据,计算盘管弯曲半径、每层盘管长度及盘管总长:
(24)
(25)
(26)
式中:Ri为第i层盘管弯曲半径,m;Li为每层盘管长度,m;Lp为盘管总长,m;Ni为盘管层数;M为每层连续管的排数,1。
假设连续管为3500 m,垂直井深为2161 m,K = 1.0 Pa∙sn,n = 0.5,ρ = 1.2 g/cm3,盘管最大为5层,按不同的钻深来计算各段的压耗及总的循环压耗。由计算结果可知,尽管增加Q值可以增加流体的紊流度,但是盘管中的压耗不仅仅与雷诺数有关,而且与流体流速的平方成正比关系,所以尽管增加流量可以提高流体的紊流程度,但是由于流体的流速也增大,所以随着Q值的增大,盘管中压耗也会随之增大。当Q值在0.006 m3/s以下时,直管内为层流;当Q值大于0.01 m3/s及以上时为紊流。 随着Q值的增大,直管的压耗也随之增大。分别计算了不同钻深(200、500、800、1100、1339 m)直管中的压耗,此时连续管直管长度分别为2161、2361、2661、2961、3261、3500 m,当连续管直管长度为3500 m时,盘管长度为0 m,连续管直管越长,管中压耗越大。由于垂直管段到水平管段连续管的曲率半径很大,所以在计算中忽略了造斜段的压耗。
当K = 1.0 Pa∙sn,n = 0.5,ρ = 1.2 g/cm3时,在流量为0.004~0.012 m3/s范围内,套管环空、油层环空以及井眼环空内的流型均为层流,总体而言,相比盘管中的压耗和直管中的压耗,各段环空中的压耗均不算太大。由于老井部分是固定不变的,所以在相同的条件下表层套管环空和油层套管环空中的压耗均不发生变化,环空中压耗的大小主要随井眼环空长度的变化而变化。计算结果表明,随着Q值的增加,各段环空的压耗均呈增大趋势。对于井眼环空,仅计算了钻进200、500、800、1100、1339 m的情况,随着环空长度的增加,压耗也随之增大。
图1是不同钻深情况下,井眼环空、直管、盘管压耗以及循环总压耗的情况比较,由图可知,从钻进开始,到钻进结束1339 m,连续管直管和环空段的压耗呈线性增加,而且增加的幅度也基本相差不大,盘管段的压耗呈线性减小,这主要是因为直管段和井眼的长度在不断增加,而盘管段的长度在不断地减小,三者综合作用的结果,使总的循环压耗略有上升,但是整体变化不大。这与郭晓乐等人 [16] 的研究结果大体相符。郭晓乐等人结合Wright等人 [17] [18] [19] 的研究,建立了连续管钻小井眼水平井循环压耗计算方法并对其规律进行了分析,他们的计算结果表明,增加连续管的弯曲度会增加压耗,而且增加幅度还随钻井液流量增加而增大。常规钻井时泵压随测深增加,在连续管钻井中,由于盘管段的内压耗要大于直管段,随测深增加,盘管段一部分进入直管段,使管内压耗减小,另一方面,随着测深的增加,环空压耗增加,两者综合使总压耗变化不大,从而使泵压的波动也不大,甚至在某些情况下还会略有减小。

Figure 1. The pressure loss in each section at different drilling depths
图1. 不同钻深时各段压耗的变化情况
图2是钻进深度为800 m,流量对盘管、连续管直管、环空总压耗以及总循环压耗的影响情况。由图可知,所有压耗均随着流量的增加呈增加的趋势,比较而言,环空压耗和盘管压耗增加较为缓慢,而且环空压耗增加的幅度小于盘管压耗,说明流量Q对环空压耗和盘管压耗的影响较小。连续管直管在前段增加缓慢,但是当流量大于0.06 m3/s以后,增加的幅度变大,这也说明当流量较小时,对各段的压耗影响较小,但是当流量相对比较大时,对连续管直管段的影响较大,而对环空和盘管的影响较小。总的循环压耗也主要是受连续管直管段的影响,当流量比较小时,总的循环压耗变化幅度较小,但是当流量变化比较大时,则总的循环压耗变化也比较大。因此,如果从降低循环压耗的角度而言,适用于用较低的Q值,但是太低的Q值一方面无法驱动井底马达,另一方面也会降低马达的效率,因此从提高马达效率的角度而言,Q值越大应该是越合适的。综合考虑马达驱动和钻屑携带,选择Q值为0.008~0.01 m3/s应该是合理的。

Figure 2. The effect of flow rate on the pressure loss in each section at 800 m
图2. 钻深为800 m时流量对各段压耗的影响
图3是不同钻深时流量对总压耗的影响情况。由图可知,在不同钻深时,随着流量的增加,总循环压耗均不断增大。同样流量的情况下,随着钻深的增加,压耗也随之增大,但是随着流量的增加,钻深对总循环压耗的影响越来越小,当流量为0.012 m3/s时,钻进前、钻进中以及钻进完毕时,总的循环压耗均在15.3 MPa左右,接近一个定值,即所有的线都交于一点。从保证钻进过程的稳定性而言,总的循环压耗波动越小应该越合适,但是0.012 m3/s的流量已经接近泵的最大额定量,而且总的循环压耗太大,所以从这个角度考虑,选用0.01 m3/s的流量是合适的。

Figure 3. The effect of Q on the total circulating pressure loss at different drilling depths
图3. 不同钻深时流量对总循环压耗的影响
3.2. n值对循环压耗的影响
图4是n值对盘管段压耗的影响图,K = 1.0 Pa∙sn,Q = 0.01 m3/s,ρ = 1.2 g/cm3。由图可以看出,随着盘管长度的增加,以及n值的增加,压耗都会不断增大,盘管越长,相同长度的盘管中n值越大,压耗的差距也越大。也就是说随着n值的增大和钻深的增加,盘管中的压耗增加幅度会变大。因此为了保证较低的压耗,更适于用相对较低的n值。

Figure 4. The effect of n on the pressure loss of each section of CT twisting in reel
图4. n值对盘管段压耗的影响
从n值对连续管直管段压耗影响的计算结果表明,随着n值的增大,雷诺数降低,摩擦因子变大,当n值较小时,直管中的流型为紊流;当n值大于0.6时,直管中的流型变为层流。n值增大,直管中的压耗也随之增大,从降低压耗的角度来考虑,n值越小越利于直管压耗的降低。从n值对环空中压耗影响的计算结果表明当n在0.2~0.7之间时,表层套管中的流体流型全部为层流,油层套管只有n = 0.2时为过渡流,其他取值下均为层流。在井眼环空中,当n在0.3以下时,流体流型为紊流,n大于0.4时为层流。尽管n值的变化会引起流体流型的变化,但是流型的变化对环空中的压耗影响并不明显,整体而言,不论是在表层套管环空和油层套管环空中,还是在井眼环空中,压耗均随n 值的增大而增大。
图5是钻进深度为800 m时,n值对各段压耗的影响曲线。由图可知,随着n值的增加,连续管盘管和直管均呈线性增加,而且直管增加的幅度比盘管段要大。当n值较小时,环空中的压耗增加较为缓慢,而当n值较大时,环空中的压耗增长幅度相对较大。随着n值的增加,总的循环压耗也不段增加,而且随着n值的增大,总循环压耗增加的幅度也越明显,因此n值的选择不宜过大。
图6是不同钻深下n值对循环压耗的影响图。从图中可以看出,随着n值的增加,总的循环压耗增大。当n值较小时,不同钻深下的总循环压耗比较接近,特别是当n = 0.45时,钻进过程中压耗基本上为一定值,随着n值的增加,总压耗的差距越来越大,钻得越深,总压耗相差越大。由图6还可以看出,随着钻进深度的增加,n值对循环压耗的影响也越来越大。

Figure 5. The effect of n on the pressure loss of each section at 800 m
图5. 钻深为800 m时n值对各段压耗的影响

Figure 6. The effect of n on the total circulating pressure loss at different drilling depths
图6. 不同钻深下n值对总循环压耗的影响
3.3. K值对循环压耗的影响
当Q = 0.01 m3/s,n = 0.5,ρ = 1.2 g/cm3时,随着K值的增大,循环压耗也随之增大,特别是当K值为1.9 Pa∙sn时,管内流体流型变为层流,此时循环压耗变得非常大,管长为1339 m时,如果取K值为2.2 Pa∙sn,则盘管中的压耗达到30.88 MPa,比K值为1.9 Pa∙sn时大了4倍多,所以为了减小盘管内的压耗,K值不能选得过大,以避免流型进入到层流状态而使盘管中的压耗增加。计算结果表明,在给定的K值范围内,流体经历了3种流型,当K值小于1.0 Pa∙sn,直管中流体为紊流;当K值为1.3 Pa∙sn时,流体为过渡流;当K值大于1.6 Pa∙sn时,流体为层流。在紊流和层流区,随着K值的增大直管中的压耗也都增大,但是刚由紊流变为层流时的区域,层流时的压耗反倒比紊流的要小,只是差距比较接近,这一点跟盘管中的情况是刚好相反的。
除了在K值很小的情况下,油层套管环空和井眼环空中会出现紊流情况,其他时候均保持在层流状态。所有环空里面的情况是一致的,也就是随着K值的增大,环空中的压耗也随之增大。由于表层套管环空的长度较短,加之半径较大,所以压耗均比较低。在油层套管环空中,当K值较低时,压耗相对而言比较小,但是当K值较大的时候,压耗也变得比较大而不能忽略。
图7是在800 m钻深时,不同K值下各段的压耗比较情况。由图7可知,随着K值的增大,井眼环空中的压耗基本上呈线性增加,在K值小于1.9 Pa∙sn时盘管中的压耗也基本呈线性增加,但是增加的幅度相较井眼环空中的压耗要小;当K值大于1.9 Pa∙sn后,盘管中流体的流型变为层流,压耗大幅度增加。对于直管而言,当K值在1.6 Pa∙sn以下时为紊流,随着K值的增加,压耗呈缓慢上升趋势;当K值为1.6 Pa∙sn时,直管的流型变为层流,从图中可以看出,在直管中当流型变为层流时,压耗反倒降低,在同样是层流的情况下,随着K值的增加,压耗也不断地增大。从以上计算数据可知,为了降低循环压耗,K值的选择不宜太高,但是考虑到钻屑的有效携带,K值也不能选得太低,所以在考虑钻屑有效携带的情况下,可以适当降低K值。K值在0.1~1.0 Pa∙sn范围内的循环压耗差值并不算大,根据理论计算的结果并结合实践经验,将K值选择在0.7~1.0 Pa∙sn的范围内是比较合适的。
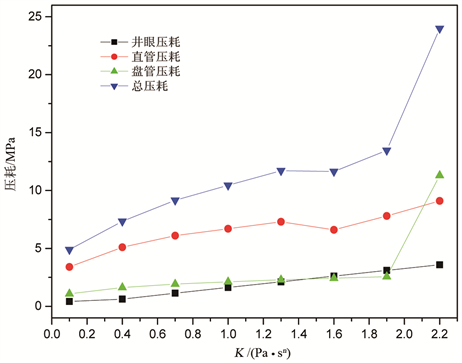
Figure 7. The effect of K on the pressure loss of each section at 800 m
图7. 钻深为800 m时K值对各段压耗的影响
图8是不同钻深时K值对总循环压耗的影响情况,图中的嵌入图为局部放大图。由图可知,随着K值的增加,不同钻深时的压耗均呈整体上升趋势,当K值为1.9 Pa∙sn时,由于盘管中的流型变为层流,使总压耗大幅度增加;当K值小于0.7 Pa∙sn时,随着钻深的增加,总的循环压耗变小,当K值等于0.7 Pa∙sn时,钻深对循环压耗基本无影响,但是当K值大于0.7 Pa∙sn以后,随着钻深的增加,循环压耗也开始增加,由于直管中流型由紊流变为层流压耗也变小,所以1.3 Pa∙sn到1.6 Pa∙sn的阶段总的压耗变化不大。如果考虑钻进过程总的循环压耗保持稳定,无疑K值为0.7 Pa∙sn是最为合适的,但是如果考虑钻屑的有效携带,K值可以选择0.7~1.0 Pa∙sn的范围。
综合以上计算结果,并结合实践经验,也就是一方面保证相对较小和较为稳定的总循环压耗,另一方面考虑钻屑的有效携带,因此对于水基钻井液而言,Q值选择在0.01 m3/s左右,n值选择在0.4~0.5,K值选择在0.7~1.0 Pa∙sn是较为合适的。

Figure 8. The effect of K on the total circulation pressure loss at different drilling depths
图8. 不同钻深时K值对总循环压耗的影响
4. 结论
以辽河油田某区块作为研究对象,以该区块的地质、钻井及钻具等参数作为计算依据,对连续管钻井中各段压耗包括连续管盘管压耗、连续管直管压耗、环空压耗以及总循环压耗进行了相应的计算。重点探讨了钻井液流量Q,稠度系数K以及流性指数n对连续管各段压耗和总循环压耗的影响。
1) 各段压耗以及总循环压耗均随着流量Q的增加而增加,但是流量Q对环空压耗和盘管压耗的影响相对较小。对直管段而言,只有当流量大于0.06 m3/s时,对压耗的影响才比较大。考虑到马达驱动、总循环压耗以及压耗稳定,选择0.01 m3/s作为最佳流量。
2) 随着n值的增加,连续管盘管和直管压耗均呈线性增加。当n值较小时,对环空压耗影响较小,但是较大的n值会在环空中产生较大的压耗。总循环压耗随着n值的增加而增加,而且增加的幅度也越大。结合不同钻深时的压耗计算,选择适宜的n值为0.4~0.5。
3) 随着K值的变化,流体经历了3种流型,除了当K值为1.6 Pa∙sn时,由于直管中的流体流型变为层流使直管压耗略有降低,总体而言,随着K值的增大,各段压耗及总循环均增大。当K值大于1.9 Pa∙sn后,由于盘管中的流体流型变为层流,使盘管压耗和总循环均大幅度增加。综合考虑总循环压耗、压耗稳定和钻屑的有效携带,K值宜选择在0.7~1.0 Pa∙sn。
基金项目
国家科技重大专项(2011ZX05036-006)。
文章引用
米远祝,罗 跃,黄志明. 连续管钻井循环压耗的计算
The Calculation of Circulating Pressure Loss in Coiled-tubing Drilling[J]. 石油天然气学报, 2017, 39(06): 67-78. http://dx.doi.org/10.12677/JOGT.2017.396100
参考文献 (References)
- 1. Ian, W.C. and Gu, H. (1996) Hydraulics Design in Coiled Tubing Drilling. SPE36349.
- 2. McCann, R.C. and Islas, C.G. (1996) Frictional Pressure Loss during Turbulent Flow in Coiled Tubing. SPE36345. https://doi.org/10.2118/36345-MS
- 3. Azouz, I., Shah, S.N., Vinod, P.S., et al. (1998) Experimental Investigation of Frictional Pressure Losses in Coiled Tubing. Society of Petroleum Engineers Production & Facilities, 13, 91-96. https://doi.org/10.2118/37328-PA
- 4. Rao, B.N. (2002) Friction Factor for Turbulent Flow of Non-Newtonian Fluid in Coiled Tubing. SPE74847. https://doi.org/10.2118/74847-MS
- 5. Zhou, Y. and Shah, S.N. (2006) New Friction-Factor Correlations for Non-Newtonian Fluid Flow in Coiled Tubing. SPE77960. https://doi.org/10.2118/77960-PA
- 6. Bailey, M.B. and Rosine, R.S. (2009) Comparison of Computional Fluid Dynamics of Erosion in Coiled Tubing on Reel-To-Injector Flow Area. SPE121171.
- 7. Medjani, B. and Shah, S.N. (2000) A New Approach for Predicting Frictional Pressure Losses of Non-Newtonian Fluid in Coiled Tubing. SPE60319. https://doi.org/10.2118/60319-MS
- 8. Willingham, J.D. and Shah, S.N. (2000) Friction Pressures of Newtonian and Non-Newtonian Fluids in Straight and Reeled Coiled Tubing. SPE60719. https://doi.org/10.2118/60719-MS
- 9. Shah, S.N. and Zhou, Y. (2001) An Experimental Study of the Effects of Drilling Solids on Frictional Pressure Losses in Coiled Tubing. SPE67191. https://doi.org/10.2118/67191-MS
- 10. Shah, S., Zhou, Y., Bailey, M., et al. (2009) Correlations to Predict Frictional Pressure Loss of Hydraulic Fracturing Slurry in Coiled Tubing. SPE104253. https://doi.org/10.2118/104253-PA
- 11. Zhou, Y.X. (2006) Theoretical and Experimental Studies of Power-Law Fluid Flow in Coiled Tubing. The University of Oklahoma, Oklahoma.
- 12. Hou, X.J., Zheng, H.K. and Zhao, J. (2014) Analysis of Circulating System Frictional Pressure Loss in Microhole Drilling with Coiled Tubing. The Open Petroleum Engineering Journal, 7, 22-28.
- 13. Dean, W.R. (1927) Note on the Motion of Fluid in a Curved Pipe. Philosophical Magazine, 4, 208-223. https://doi.org/10.1080/14786440708564324
- 14. Dean, W.R. (1928) Fluid Motion in a Curved Channel. Proceedings of the Royal Society of London: Series A. Containing Papers of a Mathematical and Physical Character, 121, 402-420. https://doi.org/10.1098/rspa.1928.0205
- 15. Hou, X.J., Gao, D.L. and Shen, Z.H. (2013) An Analysis of the Flow Resistance in Coiled Tubing Wound around a Reel, in Microhole Drilling. CMES-Computer Modeling in Engineering and Sciences, 89, 97-109.
- 16. 郭晓乐, 龙芝辉, 齐成伟. 连续管钻小井眼水平井水力学分析[J]. 科学技术与工程, 2013, 13(26): 7781-7786.
- 17. Wright, T. R. and Sas-Jaworsky II Jr, A. (2005) Coiled tubing Handbook. 4th Edition. Gulf Publishing Company, Houston.
- 18. Zhou, Y. and Shah, S.N. (2002) Non-Newtonian Fluid Flow in Coiled Tubing: Theoretical Analysis and Experimental Verification. SPE77708. https://doi.org/10.2118/77708-MS
- 19. Jain, S., Singhal, N. and Shah, S.N. (2004) Effect of Coiled Tubing Curvature on Friction Pressure Loss of Newtonian and Non-Newtonian Fluids-Experimental and Simulation Study. SPE90558. https://doi.org/10.2118/90558-MS