Pure Mathematics
Vol.06 No.03(2016), Article ID:17701,10
pages
10.12677/PM.2016.63042
A Lower Order Penalty Method for a Kind of Generalized Second-Order Cone Linear Complementarity Problems
Wenyu Zhao, Xiaojun Ma, Jun Ma
School of Mathematics and Information Science, Beifang University of Nationalities, Yinchuan Ningxia

Received: May 8th, 2016; accepted: May 27th, 2016; published: May 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
For a kind of generalized second-order cone linear complementary problem, using the ideas of lower order penalty function algorithm, it is converted to lower order penalty equations. We prove that the solution sequence of the lower order penalty equations converges to the solution of the generalized second-order cone complementarity problems at an exponential rate under particular conditions.
Keywords:Second-Order Cone Complementarity Problem, Low Order Penalty Method, Exponential Convergence Rate

一类广义二阶锥线性互补问题的 低阶罚函数算法
赵雯宇,马小军,马军
北方民族大学,数学与信息科学学院,宁夏 银川

收稿日期:2016年5月8日;录用日期:2016年5月27日;发布日期:2016年5月30日

摘 要
给出一类广义二阶锥线性互补问题的低阶罚函数算法。通过此算法,广义二阶锥线性互补问题被转化为低阶罚函数方程组。并且证明了低阶罚函数方程组的解序列在特定条件下以指数速度收敛于广义二阶锥线性互补问题的解。
关键词 :二阶锥互补问题,低阶罚函数算法,指数收敛速度

1. 引言
本二阶锥线性互补问题是线性互补问题的一个扩展,它在很多领域都具有广泛应用,比如工业设计、控制、金融与管理科学中 [1] - [3] 。在近十多年来,二阶锥线性互补问题得到了广泛关注,人们提出很多数值方法用于求解这类问题,例如,内点算法 [1] [2] [4] 、光滑牛顿算法 [1] [5] 、半光滑牛顿算法 [6] [7] 、矩阵分裂算法 [8] 、价值函数算法 [9] [10] 幂函数算法 [11] [12] 等。其中有些算法需要 [13] 浮点运算次数,这在问题维数 变得很大时可能不是有效的。与此同时,许多实际问题中的互补问题都需要有效的、精确的数值算法。
变得很大时可能不是有效的。与此同时,许多实际问题中的互补问题都需要有效的、精确的数值算法。
低阶罚函数算法是求解约束优化问题的重要方法 [13] [14] 。在文献 [15] 中,S. Wang和X. Yang提出幂罚函数算法用于求解线性互补问题。幂罚函数算法实际上是一种低阶罚函数算法。算法的核心是将线性互补问题转化为幂罚方程组序列。考虑到文献 [15] [16] 中指数收敛速度的良好性能,本文的目的是提出一类广义二阶锥线性互补问题的低阶罚函数算法。
考虑如下广义二阶锥线性互补问题:求向量 ,使得
,使得
 (1.1)
(1.1)
其中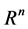 是
是 维欧式空间,
维欧式空间,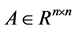 是
是 阶实矩阵,
阶实矩阵,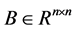 是
是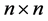 阶可逆实矩阵,
阶可逆实矩阵,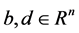 是
是 维实向量。
维实向量。
由于 可逆,故存在
可逆,故存在 ,使得
,使得 ,则
,则
 (1.2)
(1.2)
若记 ,因而(1.1)可以等价转化为:
,因而(1.1)可以等价转化为:
 (1.3)
(1.3)
因此不失一般性,本文只考虑下列形式的广义二阶锥线性互补问题:求向量 ,使得
,使得
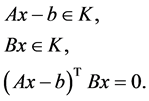 (1.4)
(1.4)
其中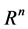 是
是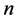 维欧式空间,
维欧式空间, 是
是 阶实矩阵,
阶实矩阵, 是
是 阶可逆实矩阵,
阶可逆实矩阵,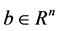 是
是 维实向量。且
维实向量。且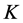 是二阶锥的笛卡尔乘积。即
是二阶锥的笛卡尔乘积。即
 (1.5)
(1.5)
其中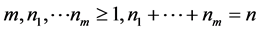 ,且
,且 看作
看作 维的二阶锥,也即
维的二阶锥,也即
 (1.6)
(1.6)
其中 表示欧几里得范数,为了方便用
表示欧几里得范数,为了方便用 来定义
来定义 。显然
。显然 是一个闭、凸的自对偶锥。如果某个
是一个闭、凸的自对偶锥。如果某个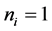 ,则
,则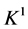 定义为非负实数集
定义为非负实数集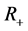 。如果
。如果 ,则
,则 退化为
退化为 。
。
本文将广义二阶锥线性互补问题(1.4)转化为带幂参数 和罚参数
和罚参数 的渐近非线性方程组(低阶罚方程组)。借助互补问题与变分不等式之间的关系,证明了广义二阶锥线性互补问题(1.4)和低阶罚方程组都是唯一可解的。并由此证明了,在矩阵
的渐近非线性方程组(低阶罚方程组)。借助互补问题与变分不等式之间的关系,证明了广义二阶锥线性互补问题(1.4)和低阶罚方程组都是唯一可解的。并由此证明了,在矩阵 正定的条件下,当罚参数
正定的条件下,当罚参数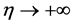 时,低阶罚方程组的解序列以指数速度
时,低阶罚方程组的解序列以指数速度 收敛于广义二阶锥线性互补问题的解。
收敛于广义二阶锥线性互补问题的解。
本文第二节给出广义二阶锥线性互补问题(1.4)的对应低阶罚方程及解得存在唯一性,第四节进行了总结。
2. 预备知识
在本节中给出单个二阶锥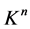 的一些基础知识。对任意的
的一些基础知识。对任意的 ,它们的Jordan product [1] 定义如下:
,它们的Jordan product [1] 定义如下:
 (2.1)
(2.1)
此处用 表示
表示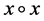 ,且
,且 表示向量的加法。这样
表示向量的加法。这样 、
、 以及
以及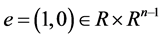 构成了
构成了 的Jordan代数。容易看出Jordan product满足交换律。一般地,约当积不满足结合律,即
的Jordan代数。容易看出Jordan product满足交换律。一般地,约当积不满足结合律,即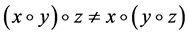 。这是研究和分析二阶锥优化算法的主要困难来源之一,但是,在内积意义下,结合律成立,即
。这是研究和分析二阶锥优化算法的主要困难来源之一,但是,在内积意义下,结合律成立,即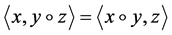 。因此对任意的正整数
。因此对任意的正整数 以及所有的正整数
以及所有的正整数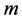 和
和 ,有
,有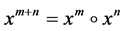 。关于与二阶锥相关的欧几里得约当代数,比如迹、行列式、可逆向量、平方根、绝对值向量,更详细的内容可参见文献 [1] [17] - [19] 。
。关于与二阶锥相关的欧几里得约当代数,比如迹、行列式、可逆向量、平方根、绝对值向量,更详细的内容可参见文献 [1] [17] - [19] 。
与矩阵的谱分解类似,在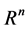 中与
中与 相关的向量也可以进行谱分解 [17] [19] ,对于
相关的向量也可以进行谱分解 [17] [19] ,对于 ,可以分解成
,可以分解成
 (2.2)
(2.2)
 (2.3)
(2.3)
 ,
,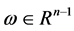 满足
满足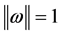 。这里
。这里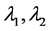 和
和 分别表示
分别表示 的特征值和相应的特征向量。如果
的特征值和相应的特征向量。如果 ,分解式(2.2)-(2.3)是唯一的。显然
,分解式(2.2)-(2.3)是唯一的。显然 且
且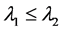 。
。
下面我们给出谱分解的一些基本性质。
性质 2.1 [4] [15] 对任意的 ,
, 、
、 和
和 、
、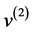 是按(2.2)和(2.3)式给定的特征值和相应的特征向量,则:
是按(2.2)和(2.3)式给定的特征值和相应的特征向量,则:
1) 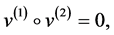
2) 
3) 
4) 是非负的(正的)当且仅当
是非负的(正的)当且仅当 。
。
5) 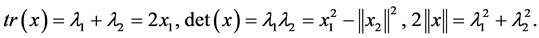
根据二阶锥的的性质,对任意的 且
且 ,有
,有 当且仅当
当且仅当 [1] [4] 。因此互补条件可以由Jordan produc的等价性来描述。根据(2.2)和(2.3)式的谱分解,一个标量值函数
[1] [4] 。因此互补条件可以由Jordan produc的等价性来描述。根据(2.2)和(2.3)式的谱分解,一个标量值函数 可以被扩展为与
可以被扩展为与 相关的一个SOC向量值函数 [4] [17] ,定义
相关的一个SOC向量值函数 [4] [17] ,定义
 (2.4)
(2.4)
其中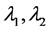 是特征值,
是特征值,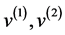 是对应的特征向量(看(2.3))。
是对应的特征向量(看(2.3))。
对任意的 ,
,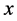 的投影定义为在
的投影定义为在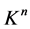 上离
上离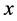 最近的点,记作
最近的点,记作 ,也即
,也即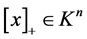 且
且
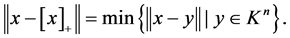 (2.5)
(2.5)
显然,当 时,投影(2.5)退化为
时,投影(2.5)退化为 。下面的引理指出当
。下面的引理指出当 时,
时,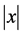 和
和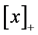 有(2.4)式的形式 [4] 。
有(2.4)式的形式 [4] 。
引理 2.1 [4] 对任意的 ,
, 、
、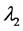 和
和 、
、 是按(2.2)和(2.3)式给定的特征值和相应的特征向量,则:
是按(2.2)和(2.3)式给定的特征值和相应的特征向量,则:
1) 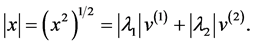
2) 对任意的标量
对任意的标量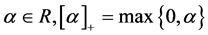 。
。
类似于在 上的投影的概念,定义
上的投影的概念,定义
 (2.6)
(2.6)
显然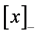 就是
就是 在
在 上投影的相反向量,且有
上投影的相反向量,且有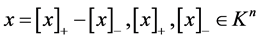 和
和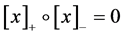 。
。
3. 低阶罚方法及收敛性分析
在本节中,针对广义二阶锥线性互补问题(1.4)提出一种低阶罚方法,以及收敛性分析的证明。不失一般性,假设向量由一个二阶锥块组成,即 ,因为收敛性分析很容易推广到一般的情况(1.5)。
,因为收敛性分析很容易推广到一般的情况(1.5)。
下面我们考虑低阶罚方程,求 ,使得
,使得
 (3.1)
(3.1)
其中 是幂参数,
是幂参数, 是罚参数。当
是罚参数。当 的谱分解为
的谱分解为 时,定义
时,定义
 (3.2)
(3.2)
当 不成立时,方程(3.1)中的罚项
不成立时,方程(3.1)中的罚项 是惩罚
是惩罚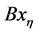 的负项。显然从方程(3.1)可以看出
的负项。显然从方程(3.1)可以看出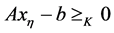 是成立的,因为
是成立的,因为 。我们希望当
。我们希望当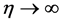 时,低阶罚方程(3.1)的解序列收敛于广
时,低阶罚方程(3.1)的解序列收敛于广
义二阶锥线性互补方程(1.4)的解。为了证明低阶罚方程解的存在性、唯一性以及解的有界性,对矩阵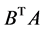 做如下假设:
做如下假设:
假设3.1 矩阵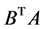 是正定的,但不一定是对称的,也即存在一个常数
是正定的,但不一定是对称的,也即存在一个常数 ,使得
,使得
 (3.3)
(3.3)
记变分不等式问题为:即求 ,使得
,使得
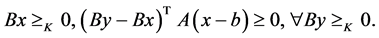 (3.4)
(3.4)
则有如下定理:
定理3.1 变分不等式(3.4)与广义二阶锥线性互补问题(1.4)等价。
证明:若 是(1.4)的解,则
是(1.4)的解,则 ,且
,且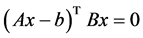 。对
。对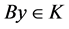 有:
有:
 (3.5)
(3.5)
因此 也是变分不等式(3.4)的解。
也是变分不等式(3.4)的解。
反之,如果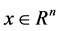 是(3.4)的解,则
是(3.4)的解,则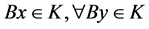 有(3.4)成立。下面证明
有(3.4)成立。下面证明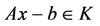 。如果不然,则必存在某个指标
。如果不然,则必存在某个指标 ,使得
,使得 。取向量
。取向量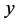 为下面方程组的解:
为下面方程组的解:
 (3.6)
(3.6)
对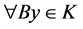 。但此时
。但此时
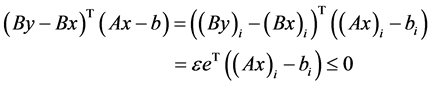 (3.7)
(3.7)
这与(3.4)矛盾,故必有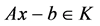 。
。
最后证明 。仍用反证法。若不然,由
。仍用反证法。若不然,由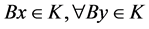 ,有
,有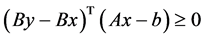 。又由
。又由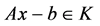 可知,必有
可知,必有 ,从而必存在某个指标
,从而必存在某个指标 ,使得:
,使得:
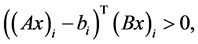
取向量 为下面方程组的解:
为下面方程组的解:
 (3.8)
(3.8)
对 。但此时
。但此时
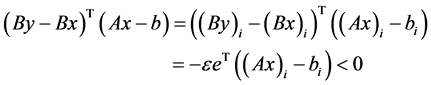 (3.9)
(3.9)
这与(3.4)矛盾,故必有 。证得广义二阶锥线性互补问题与变分不等式问题的等价性。
。证得广义二阶锥线性互补问题与变分不等式问题的等价性。
那么又由文献 [3] 中的定理2.3.3可知,变分不等式问题有唯一解,从而广义二阶锥线性互补问题有唯一解。
定理3.2 假设 正定,则低阶罚方程组(3.1)有唯一解
正定,则低阶罚方程组(3.1)有唯一解 。
。
证明:令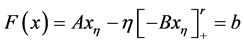 ,由于:
,由于:

证明中用到了 正定和
正定和 的分量与
的分量与 $的分量同号的事实。
$的分量同号的事实。
若令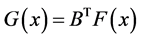 ,由上面的分析可知
,由上面的分析可知

因此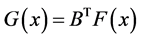 强单调,故方程组
强单调,故方程组 有唯一解(有关强单调的概念参照文献 [3] ),也即
有唯一解(有关强单调的概念参照文献 [3] ),也即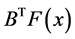 有唯一解。由于
有唯一解。由于 可逆,故方程组
可逆,故方程组 有唯一解,也即低阶罚方程组(3.1)有唯一解。
有唯一解,也即低阶罚方程组(3.1)有唯一解。
命题 3.1 对任意的 ,低阶罚方程(3.1)的解是有界的,即存在一个正常数
,低阶罚方程(3.1)的解是有界的,即存在一个正常数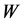 ,独立于
,独立于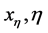 和
和 ,使得
,使得 。
。
证明:在低阶罚方程(3.1)的两边同乘以 ,得
,得
 (3.10)
(3.10)
注意到 ,我们有
,我们有
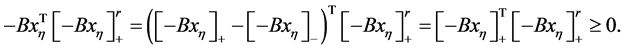 (3.11)
(3.11)
因此,由式子(3.10)和(3.11)可以得到 。结合最后一个不等式,(3.3)和Cauchy- Schwarz不等式,存在一个常数
。结合最后一个不等式,(3.3)和Cauchy- Schwarz不等式,存在一个常数 ,使得
,使得
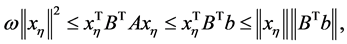 (3.12)
(3.12)
也即 。令
。令 ,得证。
,得证。
下面的性质在收敛性分析中是非常重要的,给出了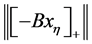 的一个上界。
的一个上界。
命题3.2 对任意的 ,存在一个正常数
,存在一个正常数 ,独立于
,独立于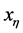 和
和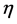 ,使得
,使得
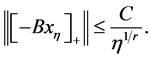 (3.13)
(3.13)
证明:令 。从(2.2)-(2.3)式可以看到
。从(2.2)-(2.3)式可以看到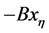 可以分解为
可以分解为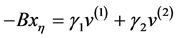 ,这
,这 是谱值,
是谱值, 表示相关的谱向量且有
表示相关的谱向量且有 。根据引理2.1,可以得到
。根据引理2.1,可以得到
 (3.14)
(3.14)
在(3.1)式的两边同乘以 ,我们可以得到
,我们可以得到
 (3.15)
(3.15)
由(3.1)式和赫尔德不等式,得到
 (3.16)
(3.16)
其中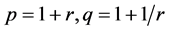 ,满足
,满足 。根据(3.2),(3.14)和性质2.1,可以得到
。根据(3.2),(3.14)和性质2.1,可以得到
 (3.17)
(3.17)
由(3.16)和(3.17)可以得到
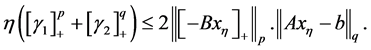 (3.18)
(3.18)
在 上由范数的等价性可知,存在一个只依赖于
上由范数的等价性可知,存在一个只依赖于 的正常数
的正常数 ,使得
,使得
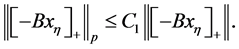 (3.19)
(3.19)
根据性质2.1,(3.14),(3.19)和三角形不等式,可以得到
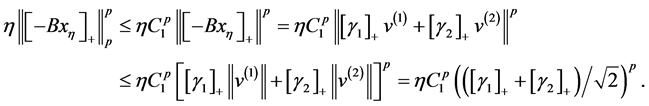 (3.20)
(3.20)
令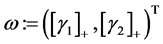 ,则对一些正常数
,则对一些正常数 有
有 。因此
。因此
 (3.21)
(3.21)
在(3.21)式的两边同时取 次幂得到
次幂得到
 (3.22)
(3.22)
由(3.18),(3.20),(3.22)可以得到
 (3.23)
(3.23)
也即 。最后一个不等式两边同时取
。最后一个不等式两边同时取 次幂得到
次幂得到
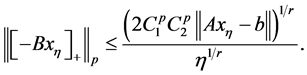 (3.24)
(3.24)
根据范数的等价性,存在一个正常数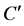 使得
使得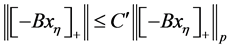 。且从(3.13)得到
。且从(3.13)得到 。所以,令
。所以,令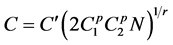 ,故(3.13)成立,证毕。
,故(3.13)成立,证毕。
由命题(4.1) (4.2)可以得到解决广义二阶锥线性互补问题的低阶罚方法的收敛结果。在此省略其证明过程,因为与文献 [15] 中定理(2.1)的证明类似。
定理3.3 对任意的 ,令
,令 是低阶罚方程组的解,且
是低阶罚方程组的解,且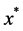 是广义二阶锥线性互补问题(1.4)的解。则存在一个独立于
是广义二阶锥线性互补问题(1.4)的解。则存在一个独立于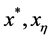 和
和 的正常数
的正常数 ,使得
,使得
 (3.25)
(3.25)
从定理4.1,可以看到当 时,低阶罚方程(3.1)的解序列
时,低阶罚方程(3.1)的解序列 以指数速率收敛到广义二阶锥线性互补问题的解。
以指数速率收敛到广义二阶锥线性互补问题的解。
定理3.3的收敛性结果是在假设3.1下成立的,若假设3.1不成立,又有什么样的收敛性结果呢?下面的定理证明在假设3.1不成立的情形下,低阶罚函数方程组(3.1)解序列的任意极限点都是广义二阶锥线性互补问题(1.4)的解,但在这种情形下不能确定收敛速度。
定理3.4 对任意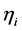 ,假设低阶罚函数方程组(3.1)有解
,假设低阶罚函数方程组(3.1)有解 ,对任意幂参数
,对任意幂参数 ,令
,令 是一列满足
是一列满足
 的正数序列,且
的正数序列,且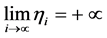 ,则序列
,则序列 的任意极限点都是广义二阶锥线性互补问题(1.4)的解。
的任意极限点都是广义二阶锥线性互补问题(1.4)的解。
证明:对任意 ,因为
,因为 是低阶罚函数方程组(3.1)关于
是低阶罚函数方程组(3.1)关于 的解,则有
的解,则有
 (3.26)
(3.26)
设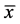 是序列
是序列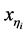 的任意极限点,不妨设当
的任意极限点,不妨设当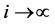 时
时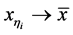 ,否则用
,否则用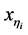 的一个子序列收敛到
的一个子序列收敛到 即可。因而存在正整数
即可。因而存在正整数 ,使得
,使得
 (3.27)
(3.27)
注意到
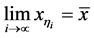 (3.28)
(3.28)
从(3.26)式得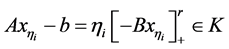 ,在此式中令
,在此式中令 ,由
,由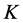 的闭性知
的闭性知
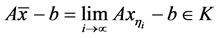 (3.29)
(3.29)
下面证明
 (3.30)
(3.30)
反设 ,此时令
,此时令 ,则
,则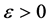 。因此,由(3.28)知当
。因此,由(3.28)知当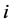 充分大时,
充分大时, 且
且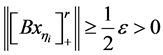 。
。
同时,由(3.26)得,当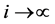 时
时
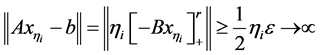
与(3.27)式矛盾,故(3.30)式成立。
下面来证明
 (3.31)
(3.31)
因为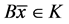 ,所以有以下三种情形:
,所以有以下三种情形:
情形一:如果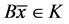 ,显然
,显然 。
。
情形二:如果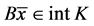 ,则
,则 。在式
。在式 中令
中令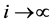 ,则
,则 。所以
。所以 。
。
情形三:如果 ,此时令
,此时令 ,则
,则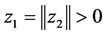 ,根据向量的特征值分解(2.2)~(2.3),
,根据向量的特征值分解(2.2)~(2.3),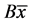 可以分解为
可以分解为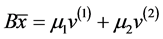 ,这里
,这里 和
和 分别表示
分别表示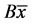 的特征值和相应的特征向量。因此
的特征值和相应的特征向量。因此
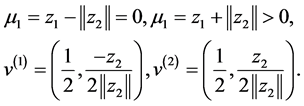
即 。假设
。假设 的特征值分解为
的特征值分解为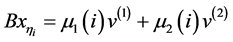 。因为对任意的
。因为对任意的 ,当
,当 时,
时, 都连续。所以由(3.28)得当
都连续。所以由(3.28)得当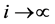 时,
时, 。特别地,当
。特别地,当 充分大时有
充分大时有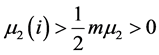 。因此,由(3.26)得
。因此,由(3.26)得
 (3.32)
(3.32)
在(3.32)式两边令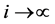 ,并记
,并记 。因此
。因此

由以上3种情形,我们得到 ,故(3.31)式成立。最后,由(3.29),(3.30)和(3.31)可得
,故(3.31)式成立。最后,由(3.29),(3.30)和(3.31)可得 是广义二阶锥线性互补问题(1.4)的解。由极限点
是广义二阶锥线性互补问题(1.4)的解。由极限点 的任意性,可知结论成立。
的任意性,可知结论成立。
4. 结论
本文根据低阶罚方程组(3.1),将低阶罚函数算法扩展到求解广义二阶锥线性互补问题(1.4)。在矩阵时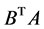 满足正定的条件下,广义二阶锥线性互补问题(1.4)与低阶罚方程组(3.1)均有唯一解,且低阶罚方程组(3.1)的解序列以指数速度收敛于广义二阶锥线性互补问题(1.4)的解。当矩阵
满足正定的条件下,广义二阶锥线性互补问题(1.4)与低阶罚方程组(3.1)均有唯一解,且低阶罚方程组(3.1)的解序列以指数速度收敛于广义二阶锥线性互补问题(1.4)的解。当矩阵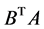 非正定时,低阶罚函数方程组的解序列仍然收敛到广义二阶锥线性互补问题的解,但不能保证以指数速度收敛。
非正定时,低阶罚函数方程组的解序列仍然收敛到广义二阶锥线性互补问题的解,但不能保证以指数速度收敛。
文章引用
赵雯宇,马小军,马 军. 一类广义二阶锥线性互补问题的低阶罚函数算法
A Lower Order Penalty Method for a Kind of Generalized Second-Order Cone Linear Complementarity Problems[J]. 理论数学, 2016, 06(03): 278-287. http://dx.doi.org/10.12677/PM.2016.63042
参考文献 (References)
- 1. Alizadeh, F. and Goldfarb, D. (2003) Second-Order Cone Programming. Mathematical Programming, 95, 3-51. http://dx.doi.org/10.1007/s10107-002-0339-5
- 2. Lobo, M.S., Vandenberghe, L., Boyd, S., et al. (1998) Appli-cations of Second-Order Cone Programming. Linear Algebra and Its Applications, 284, 193-228. http://dx.doi.org/10.1016/S0024-3795(98)10032-0
- 3. Facchinei, F. and Pang, J.S. (2003) Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer Science & Business Media.
- 4. Nemirovski, A. and Scheinberg, K. (1996) Extension of Karmarkar’s Algorithm onto Convex Quadratically Constrained Quadratic Problems. Mathematical Programming, 72, 273-289. http://dx.doi.org/10.1007/BF02592093
- 5. Chen, X.D., Sun, D.F. and Sun, J. (2003) Complementarity Functions and Numerical Experiments for Second-Order Cone Complementarity Problems. Computational Optimization and Applications, 25, 39-56. http://dx.doi.org/10.1023/A:1022996819381
- 6. Kanzow, C., Ferenczi, I. and Fukushima M. (2009) On the Local Convergence of Semismooth Newton Methods for Linear and Nonlinear Second-Order Cone Programs without Strict Complementarity. SIAM Journal on Optimization, 20, 297-320. http://dx.doi.org/10.1137/060657662
- 7. Pan, S. and Chen, J.S. (2009) A Damped Gauss-Newton Method for the Second-Order Cone Complementarity Problem. Applied Mathematics and Optimization, 59, 293-318. http://dx.doi.org/10.1007/s00245-008-9054-9
- 8. Hayashi, S., Yamaguchi, T., Yamashita, N., et al. (2005) A Matrix-Splitting Method for Symmetric Affine Second- Order Cone Complementarity Problems. Journal of Computational and Applied Mathematics, 175, 335-353. http://dx.doi.org/10.1016/j.cam.2004.05.018
- 9. Chen, J.S. and Tseng, P. (2005) An Unconstrained Smooth Mi-nimization Reformulation of the Second-Order Cone Complementarity Problem. Mathematical Programming, 104, 293-327. http://dx.doi.org/10.1007/s10107-005-0617-0
- 10. Chen, J.S. (2006) Two Classes of Merit Functions for These Cond-Order Cone Complementarity Problem. Mathematical Methods of Operations Research, 64, 495-519. http://dx.doi.org/10.1007/s00186-006-0098-9
- 11. Hao, Z., Wan, Z. and Chi, X. (2015) A Power Penalty Method for Second-Order Cone Linear Complementarity Problems. Operations Research Letter, 43, 137-142. http://dx.doi.org/10.1016/j.orl.2014.12.012
- 12. Hao, Z., Wan, Z. and Chi, X. (2015) A Power Penalty Method for Second-Order Cone Nolinear Complementarity Problems. Journal of Computational and Applied Mathematics, 290, 136-149. http://dx.doi.org/10.1016/j.cam.2015.05.007
- 13. Zangwill, W.I. (1967) Non-Linear Programming via Penalty Functions. Management Science, 13, 344-358. http://dx.doi.org/10.1287/mnsc.13.5.344
- 14. Luo, Z.Q., Pang, J.S. and Ralph, D. (1996) Mathematical Programs with Equilibrium Constraints. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511983658
- 15. Wang, S. and Yang, X. (2008) A Power Penalty Method for Linear Complementarity Problems. Operations Research Letters, 36, 211-214. http://dx.doi.org/10.1016/j.orl.2007.06.006
- 16. Huang, C. and Wang, S. (2010) A Power Penalty Approach to a Nonlinear Complementarity Problem. Operations Research Letters, 38, 72-76. http://dx.doi.org/10.1016/j.orl.2009.09.009
- 17. Chen, J.S. (2006) The Convex and Monotone Functions Asso-ciated with Second-Order Cone. Optimization, 55, 363- 385. http://dx.doi.org/10.1080/02331930600819514
- 18. Faraut, J. and KorSnyi, A. (1994) Analysis on Symmetric Cones. Oxford University Press, Oxford.
- 19. Fukushima, M., Luo, Z.Q. and Tseng, P. (2002) Smoothing Functions for Second-Order-Cone Complementarity Problems. SIAM Journal on Optimization, 12, 436-460. http://dx.doi.org/10.1137/S1052623400380365