Pure Mathematics
Vol.
12
No.
11
(
2022
), Article ID:
58581
,
11
pages
10.12677/PM.2022.1211220
有关抛物面上测地线的研究
吴钰莹,包图雅*
内蒙古民族大学数理学院,内蒙古 通辽
收稿日期:2022年10月23日;录用日期:2022年11月22日;发布日期:2022年11月30日

摘要
从方程的角度求解曲面上的测地线,是我们求测地线的常用方法。但是这种方法在求一些具体问题时计算量很大,同时也不利于人们对于曲面上测地线的直观想象。本文从测地曲率几何意义的角度出发,求出了椭圆抛物面、旋转抛物面和双曲抛物面上经过原点的所有平面曲线类型的测地线,求解过程简单,有助于人们直观理解,并利用数学软件Mathematica画出了测地线的图像。
关键词
测地曲率,抛物面,测地线

Research on Geodesics on Parabolic Surfaces
Yuying Wu, Tuya Bao*
College of Mathematics and Physics, Inner Mongolia Minzu University, Tongliao Inner Mongolia
Received: Oct. 23rd, 2022; accepted: Nov. 22nd, 2022; published: Nov. 30th, 2022

ABSTRACT
Solving geodesics on surfaces from the perspective of equations is a common method we use to find geodesics. However, this method is very computationally intensive when solving some specific problems, and it is also not conducive to people’s intuitive imagination of geodesics on surfaces. In this paper, from the perspective of the geometric meaning of geodesic curvature, the geodesic of all plane curve types passing through the origin on elliptic paraboloid, rotating paraboloid and hyperbolic paraboloid are obtained, and the solution process is simple and helpful for people to intuitively understand, and use the mathematical software Mathematica to draw the geodesic image.
Keywords:Geodesic Curvature, Parabolic Surface, Geodesic

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
测地线又称为短程线,在数学上可以理解为平面上的直线在曲面上的推广,用于描述曲面上两点之间的最短曲线,是微分几何中的重要概念。它不仅在数学内部有着十分重要的作用,在物理学、工程学和大地测量学等方面也有广泛的应用。通过曲面上测地线的形状和性质,可以分析曲面的结构和性质。比如,球面上的测地线必在球面的大圆上 [1],因为大圆在其上每一点处的切平面上的正投影曲线为直线,而小圆显然不是。为了更好地应用测地线,求出测地线的方程是一个有效途径。测地线方程可以由多种方法推导出来,参考文献 [2] 利用测地线的定义分析了曲线成为测地线的条件;参考文献 [3] 通过Liouville公式求出了旋转双曲面、正螺面和平面这些具有正交坐标网的曲面上的测地线族,再利用曲面之间的等距对应关系求出了螺旋面、悬链面和抛物柱面上的测地线族;参考文献 [4] 根据测地线的几何性质,应用微分方程及变分法从数学角度阐述了椭圆柱面上测地线的求解方法;参考文献 [5] 通过参数变换为双曲抛物面建立曲率线网参数表示,由此确定该曲面上所有平面曲线类型的测地线。其中参考文献 [5] 在求测地线的过程中借助数学软件Maple编程辅助计算,计算量很大,同时也不利于对曲面上测地线的直观想象。求测地线方程的方法很多,但寻找到一种求解过程简单、有助于人们直观理解的推导方法是不容易的。本文利用测地曲率的几何意义,做出抛物面上原点处以法线为轴的法截面束,以法截面和曲面的交线即法截线为研究对象,通过判断法截面与法截线上除原点外任意一点的切平面是否垂直来判断法截线向其上每点处切平面作正投影的曲线是否为直线,以此求出了椭圆抛物面、旋转抛物面和双曲抛物面上经过原点的平面曲线类型的测地线方程,并利用数学软件Mathematica画出了测地线的图像。
定义1 [6] 所有投射线相互平行的投影称为平行投影,投射线与投影面相互垂直的平行投影称为正投影。
下面我们给出测地曲率的几何意义。
命题1 [7] [8] 曲面S上的曲线(C),它在P点的测地曲率kg的绝对值等于(C)在P点的切平面Π上的正投影曲线( )的曲率k。
直线的曲率为0 [7],那么根据测地曲率的几何意义,我们知道曲面S上曲线(C)在其上每一点处的切平面上的正投影曲线为直线时,曲线的测地曲率为0,是测地线。
引理1 [9] 如果两个平面
交于一条直线L,那么以直线L为轴的有轴平面束的方程是
其中 是不全为零的任意实数。
引理2当两平面垂直时,其中一个平面上的曲线在另一个平面上的正投影曲线为直线,否则为曲线。
证:当两平面垂直时(见图1), 上的任意点正投影到两平面的交线上,所以 上任意曲线在 上的正投影为直线。当两平面不垂直时(见图2), 上非直线的任意曲线在 上的正投影都不是直线。
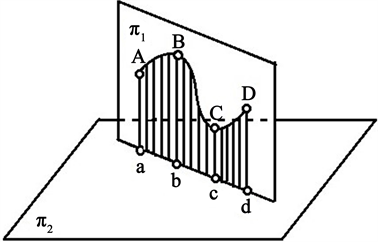
Figure 1. The two planes are perpendicular
图1. 两平面垂直
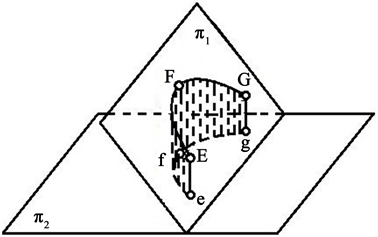
Figure 2. The two planes are not perpendicular
图2. 两平面不垂直
2. 主要结果
曲面上如果存在直线,则此直线一定是测地线 [7],故下面只寻找曲面上非直线的测地线。
定理1椭圆抛物面 上经过原点的非直线的平面曲线类型的测地线有且仅有两条,分别为 和 。
证:椭圆抛物面 的一般方程为 。
令 ,则 。
所以椭圆抛物面在点 处的切平面方程为
.
法线方程为
.
则法线的一般方程为
,
即
.
所以椭圆抛物面一点处的法截面束为
,
即
.
其中 是不全为零的任意实数。
因为
,
所以椭圆抛物面每点处的法截面与该点处的切平面垂直。
当 为原点 点时,法截面束与椭圆抛物面相交得到的法截线为
,
存在三种情况:
① 时法截面方程为 ,法截线的参数方程为
. (1)
② 时法截面方程为 ,法截线的参数方程为
. (2)
③ 时法截面方程为 ,法截线的参数方程为
. (3)
情况①中法截线(1)上除原点外任意一点 处的切平面方程为
.
因为
,
所以通过(1)的法截面 与(1)上任意一点处的切平面都垂直。
从而由引理2知法截线(1)在其上任意点处的切平面上的正投影曲线为直线,是测地线。
情况②中法截线(2)上除原点外任意一点 处的切平面方程为
.
因为
,
所以通过(2)的法截面 与(2)上任意一点处的切平面都垂直。
从而由引理2知法截线(2)在其上任意点处的切平面上的正投影曲线为直线,是测地线。
情况③中法截线(3)上除原点外任意一点 处的切平面方程为
.
因为
,
所以通过(3)的法截面 与(3)上除原点外任意一点处的切平面都不垂直,由引理2知法截线(3)在其上任意点处的切平面上的正投影曲线都不是直线,则法截线(3)不是测地线。
从而椭圆抛物面 上经过原点的非直线的平面曲线类型的测地线方程有且仅有两条,分别为 和 。
下面给出椭圆抛物面上测地线向原点处切平面作正投影的图像(见图3),其中红色线曲线是测地线,绿色曲线是测地线在原点处切平面上的正投影曲线。
定理2旋转抛物面 上原点处的法截面束与旋转抛物面相交得到的法截线都是测地线。
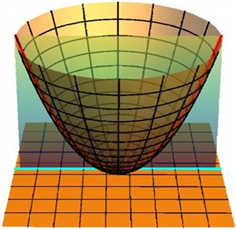 (a)
(a)
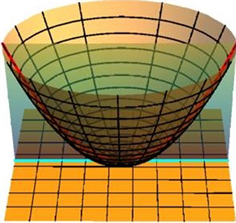 (b)
(b)
Figure 3. Orthographic projection of the geodesic of the elliptic paraboloid at the origin (a) (b)
图3. 椭圆抛物面上测地线在原点处作正投影(a) (b)
证:旋转抛物面 的一般方程为 。
令 ,则 。
所以旋转抛物面在点 处的切平面方程为
.
法线方程为
.
则法线的一般方程为
,
即
.
所以旋转抛物面一点处的法截面束为
,
即
.
其中 是不全为零的任意实数。
因为
,
所以旋转抛物面每点处的法截面与该点处的切平面垂直。
当 为原点 点时,法截面束与旋转抛物面相交得到的法截线为
,
存在三种情况:
① 时法截面方程为 ,法截线的参数方程为
. (4)
② 时法截面方程为 ,法截线的参数方程为
. (5)
③ 时法截面方程为 ,法截线的参数方程为
. (6)
情况①中法截线(4)上除原点外任意一点 处的切平面方程为
.
因为
,
所以通过(4)的法截面 与(4)上任意一点处的切平面都垂直。
从而由引理2知法截线(4)在其上任意点处的切平面上的正投影曲线为直线,是测地线。
情况②中法截线(5)上除原点外任意一点 处的切平面方程为
.
因为
,
所以通过(5)的法截面 与(5)上任意一点处的切平面都垂直。
从而由引理2知法截线(5)在其上任意点处的切平面上的正投影曲线为直线,是测地线。
情况③中法截线(6)上除原点外任意一点 处的切平面方程为
因为
,
所以通过(6)的法截面 与(6)上任意一点处的切平面都垂直。
从而由引理2知法截线(6)在其上任意点处的切平面上的正投影曲线为直线,是测地线。
综上旋转抛物面 上原点处的法截面束与旋转抛物面相交得到的法截线都是测地线。
下面给出旋转抛物面上部分测地线向原点处切平面作正投影的图像(见图4),其中红色线曲线是测地线,绿色曲线是测地线在原点处切平面上的正投影曲线。

Figure 4. Orthographic projection of the geodesic of the rotating paraboloid at the origin
图4. 旋转抛物面上测地线在原点处作正投影
定理3双曲抛物面 上经过原点的非直线的平面曲线类型的测地线有且仅有两条,分别为 和 。
证:双曲抛物面 的一般方程为 。
令 ,则 ,
所以双曲抛物面在点 处的切平面方程为
.
法线方程为
.
法线的一般方程为
,
即
.
则双曲抛物面一点处的法截面束为
,
即
.
其中 是不全为零的任意实数。
因为
,
所以双曲抛物面每点处的法截面与该点处的切平面垂直。
当 为原点 点时,法截面束与双曲抛物面相交得到的法截线为
,
存在三种情况:
① 时法截面方程为 ,法截线的参数方程为
. (7)
② 时法截面方程为 ,法截线的参数方程为
. (8)
③ 时法截面方程为 ,法截线的参数方程为
. (9)
情况①中法截线(7)上除原点外任意一点 处的切平面方程为
.
因为
,
所以通过(7)的法截面 与(7)上任意一点处的切平面都垂直。
从而由引理2知法截线(7)在其上任意点处的切平面上的正投影曲线为直线,是测地线。
情况②中法截线(8)上除原点外任意一点 处的切平面方程为
.
因为
,
所以通过(8)的法截面 与(8)上任意一点处的切平面都垂直。
从而由引理2知法截线(8)在其上任意点处的切平面上的正投影曲线为直线,是测地线。
情况③中法截线(9)上除原点外任意一点 处的切平面方程为
.
因为
,
所以通过(9)的法截面 与(9)上任意一点处的切平面都不垂直,由引理2知法截线(9)在其上任意点处的切平面上的正投影曲线都不是直线,则法截线(9)不是测地线。
从而双曲抛物面 上经过原点的非直线的平面曲线类型的测地线方程有且仅有两条,分别为 和 。
下面给出双曲抛物面上测地线向原点处切平面作正投影的图像(见图5),其中红色线曲线是测地线,绿色曲线是测地线在原点处切平面上的正投影曲线。
 (a)
(a)
 (b)
(b)
Figure 5. Orthographic projection of the geodesic of the hyperbolic paraboloid at the origin (a) (b)
图5. 双曲抛物面上测地线在原点处作正投影(a) (b)
3. 结论
本文利用测地曲率的几何意义求出了抛物面上经过原点的平面曲线类型的测地线,为测地线的求法提供了新思路。目前本文的工作仅针对于经过曲面原点的测地线,将本文的方法应用到求经过曲面任意一点的测地线的可行性也是值得研究的。
致 谢
作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见。
基金项目
国家自然科学基金(11661062);
内蒙古自然科学基金(2022MS01015);
内蒙古自治区高等学校青年科技英才支持计划(NJYT-19-A09)。
文章引用
吴钰莹,包图雅. 有关抛物面上测地线的研究
Research on Geodesics on Parabolic Surfaces[J]. 理论数学, 2022, 12(11): 2033-2043. https://doi.org/10.12677/PM.2022.1211220
参考文献
- 1. 邢家省, 高建全, 罗秀华. 曲面上测地线和短程线的性质[J]. 四川理工学院学报(自然科学版), 2015, 28(1): 63-66+86.
- 2. 刘晓周, 包图雅. 关于复射影空间中A2型实超曲面上Sasaki磁场下的轨道研究[D]: [硕士学位论文]. 通辽: 内蒙古民族大学, 2022.
- 3. 吴钰莹, 包图雅, 刘晓周. 等距对应视角下的测地线[J]. 大学数学, 2022, 38(5): 17-22.
- 4. 林大钧, 郭慧, 展益彬. 椭圆柱面上测地线的几种求解方法研究[J]. 东华大学学报(自然科学版), 2005(4): 79-81.
- 5. 张量, 宋卫东. 双曲抛物面上的曲率线网及其应用[J]. 高等数学研究, 2014, 17(4): 53-54.
- 6. 谷超豪. 数学词典[M]. 上海: 上海辞书出版社, 1992: 165-166.
- 7. 梅向明, 黄敬之. 微分几何[M]. 第4版. 北京: 高等教育出版社, 2008.
- 8. 闫德宝. 测地曲率几何意义的证明[J]. 理论数学, 2021, 11(3): 319-322. https://doi.org/10.12677/PM.2021.113042
- 9. 吕林根, 许子道. 解析几何[M]. 第4版. 北京: 高等教育出版社, 2006.
NOTES
*通讯作者。