Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18469,24
pages
10.12677/AAM.2016.53064
Study on the Mathematical Problems of Generalized Uncertainty Principles
Guanlei Xu1, Xiaotong Wang2, Lijia Zhou1, Limin Shao1, Yonglu Liu1, Xiaogang Xu2
1Ocean Department of Dalian Navy Academy, Dalian Liaoning
2Navigation Department of Dalian Navy Academy, Dalian Liaoning

Received: Aug. 11th, 2016; accepted: Aug. 25th, 2016; published: Aug. 31st, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The uncertainty principle is the elementary rule in the crossed fields of mathematics, information and physics and so on, which plays an important role in scientific sense and engineering value. This paper discussed the mathematical problems in the research of widely studied generalized uncertainty principles (i.e., the generalized uncertainty principles on time-frequency analysis and the generalized uncertainty principles on sparse representation), including the extension of the traditional inequalities to the generalized domains, the optimization of various p-norms, the optimal matrix factorization and so on. The review of these mathematical problems is the focus in this paper, and the disadvantages and the future work of these mathematical problems are discussed as well.
Keywords:Generalized Uncertainty Principle, Sparse Representation, Time-Frequency Analysis, Resolution Analysis, Norm, Entropy, Matrix Factorization

广义测不准原理中的数学问题研究
徐冠雷1,王孝通2,周立佳1,邵利民1,刘永禄1,徐晓刚2
1海军大连舰艇学院军事海洋系,辽宁 大连
2海军大连舰艇学院航海系,辽宁 大连

收稿日期:2016年8月11日;录用日期:2016年8月25日;发布日期:2016年8月31日

摘 要
测不准原理(Uncertainty Principle,又称不确定原理)是数学、信息学与信号处理、物理学等交叉学科中的基本法则,具有重要的理论意义和价值。本文从数学角度出发,针对近年来受到广泛关注和研究的广义不确定原理(即时频分析广义测不准原理和信号稀疏表示广义测不准原理两大方面),给出了广义不确定原理研究中所涉及的主要数学问题,包括传统数学不等式在广义域内的推导证明、信号不同范数下的优化求解、矩阵优化分解等问题,既包括特定广义域内的推导证明,又包括不同变换基函数或框架下的数学优化,对于广义测不准原理中的数学问题进行了总结,并给出了其存在的问题,讨论了下一步可能的研究思路和方向。
关键词 :广义测不准原理,稀疏表示,时频分析,分辨率分析,范数,熵,矩阵分解

1. 引言
测不准原理最初由德国物理学家Heisenberg [1] 于1927年提出,又称Heisenberg测不准原理,它的提出解释了量子力学存在的基本问题,即不能同时确定两个共轭变量(例如,位置和速度,时间和频率)的测量精度,这两个共轭变量准确度的乘积存在下界。Heisenberg测不准原理已证明其不仅是物理学领域的一个基本问题,而且在很多其它领域(数学、信息学、社会科学等)中 [2] - [31] 也是一条通用的自然法则。随着研究的深入,测不准原理得到了进一步的扩展,先后提出了应用于时频平面分辨率分析的加窗测不准原理 [4] [9] [10] [14] [20] ,数学理论中的对数测不准原理 [4] [11] [12] ,量子力学与信息学中的熵(主要包括香农熵、Renyi熵外、Tsallis熵、黑洞普朗克熵等)测不准原理 [4] [5] [8] [21] - [30] ,广义域(分数阶Fourier变换域和线性正则变换域)内的测不准原理 [31] - [56] ,信号稀疏表示 [57] - [83] 相关的广义测不准原理等,这些工作在各学科领域的理论和应用研究中发挥出了重要的作用,同时也给出了一个重要的启示:在不同的域内,测不准原理具有不同的下限,研究和获得这些下限,可以进一步指导各种理论研究和工程应用工作。
在信息领域,Heisenberg测不准原理一般来讲有两层传统含义:一是时间分辨率和频率分辨率不能够同时无限制地提高,它们的乘积存在一个下限;二是时间分辨率和频率分辨率之间存在着相互制约的关系,即如果要提高频率分辨率就得降低时间分辨率,反之亦然。但是,一直以来,测不准原理都被认为是“消极”的,人们在该领域的研究 [1] - [56] 主要是如何更深刻地理解和有效地降低这种消极程度,这类广义测不准原理我们称之为时频分析广义测不准原理。时频分析广义测不准原理把不同的基函数单独或独立对信号进行表示,一般来讲只是对信号在单域内聚集程度(或独立的两个域内聚集程度之和/积)进行理论论证和分析。
然而,最近Denoho等人的压缩感知理论 [59] - [63] 却揭示了测不准原理“积极”的一面,任何由测不准原理带来的“积极”内容都将是令人吃惊的(surprising) [69] 。例如,当某信号的基函数集的变换系数支撑之和小于某个特定值时,信号就可以用这些基函数集唯一地最佳稀疏表示,这就告诉了我们如何选择最佳的基函数集对信号进行稀疏表示,显然是“积极”的,这类广义测不准原理我们称之为稀疏表示广义测不准原理。稀疏表示广义测不准原理一般把多个基函数作为信号表示的一个整体基函数进行信号的表示分析,其目的就是阐释信号如何才能最佳稀疏表示,因此可以对信号的最佳稀疏表示进行理论和工程指导。实际上,稀疏表示理论(包括完备字典、过完备字典等概念)先于压缩感知概念 [79] [80] ,它可以看作压缩感知的组成部分,但又可独立于压缩感知理论。尽管早期的稀疏表示 [79] [80] 并不是从广义测不准原理入手的,但是目前的研究表明,稀疏表示广义测不准原理是信号稀疏表示的理论基础,可以对信号的最佳稀疏表示进行有效的理论和工程指导。
时频分析广义测不准原理 [1] - [56] 与稀疏表示广义测不准原理 [57] - [83] 最大的区别在于:稀疏表示广义测不准原理一般把多个基函数作为信号表示的一个整体基函数进行信号的表示分析,其目的就是阐释信号如何才能最佳稀疏表示,包括信号最佳稀疏表示的理论条件、信号唯一稀疏表示的边界条件、信号稀疏表示的程度和范围、信号稀疏表示的工程判据等等,因此可以对信号的最佳稀疏表示进行理论和工程指导;而时频分析广义测不准原理则把不同的基函数单独或独立对信号进行表示,一般来讲只是对信号在单域内聚集程度(或独立的两个域内聚集程度之和或积)进行理论论证和分析,多数用来分析时频分辨率及分辨率之间的关系。
本论文将从两类广义测不准原理的角度出发,针对信号处理中的广义测不准原理理论研究中所涉及的数学问题进行分析研究,给出信号处理中的广义测不准原理研究中的数学问题,旨在为更好地研究广义测不准原理的理论及其信息学中应用提供一定的依据。
2. 时频分析广义测不准原理中的数学问题
时频分析广义测不准原理把不同的基函数单独或独立对信号进行表示,一般来讲只是对信号在单域内聚集程度(或独立的两个域内聚集程度之和/积)进行理论论证和分析,多数用来分析时频分辨率及分辨率之间的关系。
时频分析广义测不准原理主要是指在分数阶Fourier变换域和线性正则变换域内的传统时频平面分辨率分析的Heisenberg测不准原理、加窗测不准原理 [4] [14] [9] [10] [20] 、对数测不准原理 [4] [11] [12] 、熵(主要包括香农熵、Renyi熵外、Tsallis熵、黑洞普朗克熵等)测不准原理 [4] [5] [8] [21] - [30] 等的扩展,把这些测不准原理从传统的时域与频域拓展到时域与广义域内(分数阶Fourier变换域和线性正则变换域内),或者拓展到广义域内与广义域内(即两个域均是分数阶Fourier变换域或线性正则变换域) [31] - [56] 。在这些广义测不准原理的推导证明过程中所涉及的主要数学公式或性质(或主要数学问题)包括:变量代换、Parseval准则、Cauchy-Schwartz不等式、Minkowski 不等式、Hausdorff-Young不等式以及Pitt不等式等数学问题。
由于分数阶Fourier变换可以作为线性正则变换的特例对待,所以本文主要以线性正则变换为例加以讨论。首先给出线性正则变换的数学定义及主要特性,以及这些特性的相关应用。然后讨论了广义测不准原理推导证明过程中常用的Minkowski不等式、广义Hausdorff-Young不等式、广义Pitt不等式、变量代换等数学问题,并给出了相应的广义形式推导和典型应用示例(具有启示作用)。
2.1. LCT基本定义和数学特性及应用
给定任意信号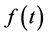 (
( ),其线性正则变换定义 [54] - [56] 如下:
),其线性正则变换定义 [54] - [56] 如下:
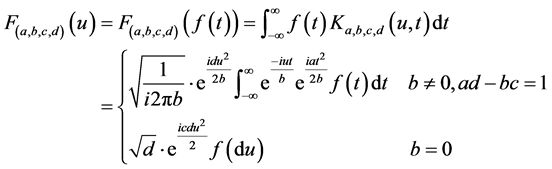 , (1)
, (1)
其主要性质:
1) 叠加特性: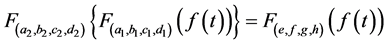 , (2)
, (2)
其中 。
。
2) 可逆性: , (3)
, (3)
其中, 。
。
3) 时移性: , (4)
, (4)
4) 尺度特性: , (5)
, (5)
5) 乘积特性: ,(6)
,(6)
6) 广义Parseval准则: . (7)
. (7)
Parseval准则/定理的物理意义是能量守恒,时域能量等于频域能量,不会因为变换而发生改变。而广义Parseval准则讨论了在广义域内(分数阶Fourier变换域和线性正则变换域内)的能量守恒问题,即时域能量等于广义频域能量。
除了Parseval准则以外,Cauchy-Schwartz不等式也是广义测不准原理证明过程中常用的数学法则。数学上,Cauchy-Schwartz不等式,又称Schwartz不等式。Cauchy-Schwartz不等式表明,若f和g是实或复内积空间的元素,则有
 ,
,
等式成立当且仅当f和g是线性相关的。Cauchy-Schwartz不等式的一个重要结果,是内积为连续函数,例如下面的证明过程:
根据乘积特性(6)和广义Parseval准则(7),可得
 , (8)
, (8)
 . (9)
. (9)
上述两式应用Cauchy-Schwartz不等式,可得
 .
.
对于实数函数 ,有
,有
 .
.
所以,进一步得到一个广义测不准原理的结果:
 .
.
Cauchy-Schwartz不等式有另一形式,还可以用范数(见论文第三部分)的写法表示:
 .
.
有关线性正则变换(及分数阶Fourier变换)的其他详细论述可参阅文献 [54] - [56] 。
2.2. Minkowski不等式
Minkowski不等式在广义测不准原理的推导中也颇为重要,首先简要回顾下Minkowski不等式的推导过程。我们考虑连续函数形式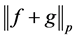 的p次幂:
的p次幂:

用三角形不等式展开:
 .
.
用赫尔德不等式,上式右侧
 .
.
利用关系式 ,最终得到Minkowski不等式:
,最终得到Minkowski不等式:
 .
.
类似地,得到多路信号的Minkowski不等式 [53] 为:
 ,
,
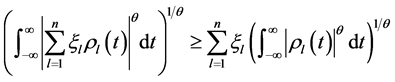 .
.
应用该公式,可以得到多路信号的广义熵测不准原理:
 .
.
2.3. 广义Hausdorff-Young不等式
使用变量替换原理,可以推导LCT域内的广义Hausdorff-Young不等式。
考虑W. Beckner的Hausdorff-Young不等式 [11] [12] [23] [26]
 ,
,
其中 ,
, ,
,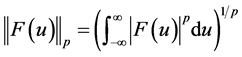 ,
, 。
。
首先假定 (
( ),且设
),且设 ,
, 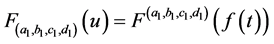 ,
, 。
。
应用等式 ,即得
,即得
 ,
,
即 .
.
由于 ,所以
,所以
 .
.
通过变量代换,并应用Fourier变换定义可得:
 .
.
令 ,即得
,即得
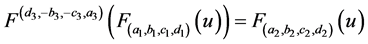 和
和 .
.
所以 .
.
所以 .
.
广义分数阶Fourier变换域的Hausdorff-Young不等式,与变换参数a、b有关,与c、d无关。
当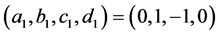 和
和 时,则
时,则
 .
.
上式是传统Hausdorff-Young不等式的第二种书写版本。特别是,当 时,即可得到广义分数阶Fourier变换域的Parseval准则
时,即可得到广义分数阶Fourier变换域的Parseval准则
 .
.
根据 和
和 的关系,即可得到广义分数阶Fourier变换域的Hausdorff-Young不等式的第二种形式
的关系,即可得到广义分数阶Fourier变换域的Hausdorff-Young不等式的第二种形式

和
 .
.
对上式两边取对数,可得
 ,
,
其中, ,
, ,
, 。
。
 .
.
根据广义分数阶Fourier变换域的Hausdorff-Young不等式, 以及Parseval准则,可得
以及Parseval准则,可得 。
。
当 时,
时,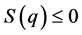 ,所以
,所以
 .
.
结合条件 ,可得
,可得
 ,
,
即 .
.
这样,就可以应用广义Hausdorff-Young不等式得到广义熵测不准原理。
2.4. 广义Pitt不等式
类似于上节,使用变量替换原理,可以推导LCT域内的广义Pitt不等式,从而进一步推导出广义对数测不准原理。
根据W. Beckner [11] [12] [23] [26] 的Pitt不等式
 ,
,
其中 ,
, ,
, 。
。
首先,不妨假定 和
和 (
( )。
)。
设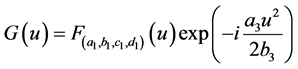 ,
, ,
, ,可得:
,可得:
 ,
,
所以 .
.
根据 的尺度特性,可得
的尺度特性,可得
 .
.
应用 ,并进行变量代换,可得
,并进行变量代换,可得
 .
.
所以
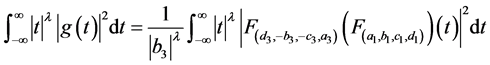 .
.
令 ,并将其代入上式,可得:
,并将其代入上式,可得:
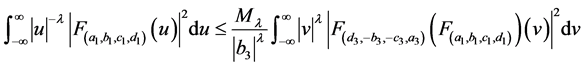 .
.
设 ,则
,则 和
和 。
。
综合上述各式,可得:
 .
.
广义分数阶Fourier变换域的Pitt不等式与变换参数a、b有关,与c、d无关,因为c和d只起尺度变换和调制的作用,其证明过程可以看出尺度变换 和调制
和调制 的影响被消除了。当
的影响被消除了。当 且
且 时,可得:
时,可得:
 .
.
上式是传统Pitt不等式的第二种书写形式。
当 时,即为Parseval准则
时,即为Parseval准则
 .
.
设
所以
 ,
,
其中,
当 时,
时, ,且
,且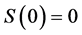 和
和 ,所以
,所以
 .
.
所以
 ,
,
即
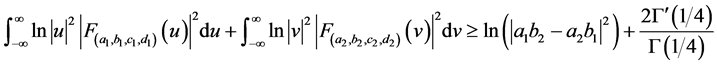 .
.
当 和
和 时,则有
时,则有
 .
.
上式为分数阶Fourier变换域内的广义对数测不准原理。
2.5. 不同广义测不准原理证明过程中的数学问题
上面几个小节只是给出了几个广义测不准原理推到证明过程中的几个数学法则或不等式的应用,本部分采用表格的方式把所有时频分析广义测不准原理对应的数学法则或不等式(数学问题)进行总结,以提供一个直观的比较和分析(其中包括我们前期研究的部分工作 [31] - [35] [41] - [43] [48] ) (表1~6)。
3. 信号稀疏表示广义测不准原理中的数学理论及方法
有关信号稀疏表示的广义测不准原理可以追溯到Denoho等人于1989年提出的理论 [60] ,其主要阐述用栅栏基信号(spikes)和正弦基信号(二者称为时频原子基)表示有限支撑的离散信号和模拟信号的测不准原理问题,给出了信号稀疏表示广义测不准原理雏形,得出了给定能量(2-范数下的定义)的离散信号所对应局部支撑乘积的下限。后来,Denoho等人又于2001年正式给出了把时频原子基作为一个具有过完备性的字典来进行信号稀疏表示的性能边界条件 [63] 。由于信号稀疏表示采用最小0-范数来进行量化和界定,但是最小0-范数的求解是个NP问题(即数学上需要把所有的情况都穷举完才能找到最优的解,目前NP问题也是困扰数学界多年的难题之一),所以Denoho等人又给出了信号稀疏表示的最小0-范数和最小1-范数等价的广义测不准原理边界条件,而最小1-范数在数学上是个凸问题,可以通过优化算法进行有效的求解,从而简化了稀疏分解问题。Denoho等人尽管只是给出了时频原子基的广义测不准原理,但是该工作在后来Patrick等人的论文 [70] 中被称之为信号稀疏表示及重构方面研究的里程碑。
在此基础上,Elad等人于2002年提出了任意两个正交基集的稀疏表示广义测不准原理 [64] ,从时频原子基扩展到任意两个正交基集,并且给出了更为严格的0-范数和1-范数等价的测不准原理边界条件。后来,Feuer和Nemirovski等人证明了这些条件是充要条件 [65] [66] 。同时,Fuchs等人也进行了类似的工作 [67] [68] 并在一些扩展空间上给出了相似的结论。
但是,从信号稀疏分解的角度来看,自然界中的信号千变万化,用两个正交基集不一定能够得到理想的稀疏表示结果,两个正交基集显然也不总是稀疏分解的基函数集的最佳选择。所以,Patrick等人于2012年又提出了两个非正交基集的广义测不准原理 [70] ,其中每个非正交基序列都是冗余的,可以独立实现对信号的稀疏表示(但不一定最佳稀疏表示),从而把两个正交基集扩展到更为一般的两个基函数集,而且优化了广义测不准原理的边界条件。2013年,Benjamin等人则从支撑和框架角度进行了时频分析广义测不准原理的理论阐述 [71] ,给出了一些新的概念和定义,为后期稀疏表示方面熵的广义测不准原理的研究提供了一定的基础。另外,Yonina则针对平移不变模拟信号进行了稀疏表示广义测不准原理的理论研究 [74] 。
在前人研究基础上,我们针对正交基集,对信号唯一最佳稀疏表示广义测不准条件、最佳稀疏表示范数和最小熵关系等进行了研究 [57] [58] 。前期研究总结表明,稀疏表示广义测不准原理的研究还处于热点研究阶段,还有很多问题没有解决,同时也表明,稀疏表示广义测不准原理属于典型的数学与信息学
Table 1. Mathematical problems of generalized Heisenberg uncertainty principles
表1. 广义Heisenberg测不准原理的数学问题
Table 2. Mathematical problems of generalized Shannon entropic uncertainty principles
表2. 广义Shannon熵测不准原理的数学问题
Table 3. Mathematical problems of generalized Rényi entropic uncertainty principles
表3. 广义Rényi熵测不准原理的数学问题
Table 4. Mathematical problems of generalized windowed uncertainty principles
表4. 广义加窗测不准原理的数学问题
Table 5. Mathematical problems of generalized logarithmic uncertainty principles
表5. 广义对数测不准原理的数学问题
Table 6. Generalized Hausdorff-Young and Pitt Inequalities
表6. 广义Hausdorff-Young不等式和广义Pitt不等式
科交叉领域,但是归根结底都可以纳入到相关的数学问题中去(比如,不同范数及范数优化、稀疏求解、稀疏矩阵及矩阵分解等)。表7概括了稀疏表示广义测不准原理的研究现状以及需要完善的研究内容,涵盖了不少数学问题,表8则概述了已有的稀疏表示广义测不准原理所涉及到的主要的数学问题。
下面就针对不同的数学问题进行展开论述。
3.1. p范数
p范数(p-norm)可以看成2范数的扩展,但是:p的范围是[1, inf)。p在(0,1)范围内定义的并不是范数
Table 7. State of the generalized uncertainty principles for signal sparse representation
表7. 稀疏表示广义测不准原理基于数学角度的理论研究现状
Table 8. Mathematical problems of generalized uncertainty principles for signal sparse representation
表8. 稀疏表示广义测不准原理的数学问题
(但是,我们有时也笼统地称之为0-范数、1/2-范数等),因为违反了三角不等式。在p范数下定义的单位球(unit ball)都是凸集(convex set,简单地说,若集合A中任意两点的连线段上的点也在集合A中,则A是凸集),但是当0 < p < 1时,在该定义下的unit ball并不是凸集(注意:我们没说在该范数定义下,因为如前所述,0 < p < 1时,并不是范数)。下图展示了p取不同值时单位圆(因为p取2时为标准的单位圆,故以单位圆为标准比对对象)的形状,见图1。
0-范数是稀疏表示中常用的范数,其物理意义就是求非零数据的个数。由于信号严格稀疏表示采用最小0-范数来进行量化和界定,但是最小0-范数的求解是个NP问题(即数学上需要把所有的情况都穷举完才能找到最优的解),所以Denoho等很多学者又给出了信号稀疏表示的最小0-范数和最小1-范数等价的广义测不准原理边界条件,然后用1-范数代替0-范数进行问题的求解。
上述范数主要针对向量,实际上矩阵也有范数,一般来讲矩阵范数除了正定性,齐次性和三角不等式之外,还规定其必须满足相容性,所以矩阵范数通常也称为相容范数。需要注意的是,如果不考虑相容性,那么矩阵范数和向量范数就没有区别。引入相容性主要是为了保持矩阵作为线性算子的特征,这一点和算子范数的相容性一致,并且可以得到Mincowski定理以外的信息。矩阵范数最常用的就是Frobenius范数(也叫Euclid范数,简称F-范数或者E-范数)和核范数。Frobenius范数即为求解矩阵A全部元素平方和的平方根。由于向量的F-范数就是2-范数,所以F-范数和向量的2-范数相容。核范数(也叫奇异值的0-范数),其物理意义是求解非零奇异值的个数,换句话说就是矩阵的最小秩求解。
关于范数的其他更详细介绍可以参照文献 [84] 。
3.2. 数学优化问题
目前常用的三种范数优化模式为P0问题、P1问题以及Pe问题:
P0问题:
 . (10)
. (10)
P1问题:
 . (11)
. (11)
Pe问题:
 , (12)
, (12)
其中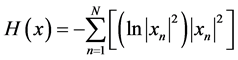 为香农熵定义式。
为香农熵定义式。
范数及熵最小优化问题涉及到的算法主要包括基追踪算法、贪婪算法、迭代阈值算法等算法。下面就三种优化各自给出一个优化算法示例,从而可以有一个比较直观的认识。
1) 基追踪算法
Chen等人 [77] 提出了一种极小化1-范数的稀疏求解思路(P1问题)。实际上,需要特别说明的是:基追踪算法并非基于一个最优化原则,其原理本质是给定一些限制条件后,通过极小化1-范数可以获得最稀疏的解。主要是通过单纯形法、内点法或对数障碍发来进行求解。它需要最少的测度,但其高算法复杂性会影响到实际大规模应用。假设线性系统 有
有 个非零的稀疏解,也就是,
个非零的稀疏解,也就是, 。而且,假设
。而且,假设 。匹配追踪或者基础追踪可以成功的恢复稀疏解吗?显而易见的,这样的成功并不是对于所有的矩阵A的所有的
。匹配追踪或者基础追踪可以成功的恢复稀疏解吗?显而易见的,这样的成功并不是对于所有的矩阵A的所有的 都可以的,因为这个可能和一般情况下的已知的NP问题发生冲突。然而,如果这个等式有一个充分稀疏的解,那么这些算法在寻址原始的目标(P0)的成功性就有所保证了。
都可以的,因为这个可能和一般情况下的已知的NP问题发生冲突。然而,如果这个等式有一个充分稀疏的解,那么这些算法在寻址原始的目标(P0)的成功性就有所保证了。

Figure 1. The different shapes of unit ball for different p
图1. p取不同值时单位圆的形状
在这里我们可以对变换矩阵 和
和 的列重新进行顺序排列,向量b被设置为
的列重新进行顺序排列,向量b被设置为 中的第一个
中的第一个 列的线性组合,也是
列的线性组合,也是 中的第一个
中的第一个 列,则有
列,则有 。所以,
。所以,
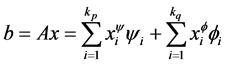 , (13)
, (13)
进一步定义所有支撑 和
和 ,分别地,我们可以得到关系式:
,分别地,我们可以得到关系式: 及
及 。
。
往往在算法第一步(k=0)中,计算误差的设置一般都是由以下的公式给出:

所以,对于在合适的 个非零元素中,其中需要处理的第一步就是,我们应该假定所有的
个非零元素中,其中需要处理的第一步就是,我们应该假定所有的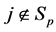 和
和 ,得到
,得到
 . (14)
. (14)
此时我们假定没有一般性损失, 是x中所有的非零元素中最大的,而且我们希望它是在这个步骤中被选择出来的。此后我们指向要求(#),然后转向相似方法中的第二个的处理。在等式(13)中这个的置换转化成
是x中所有的非零元素中最大的,而且我们希望它是在这个步骤中被选择出来的。此后我们指向要求(#),然后转向相似方法中的第二个的处理。在等式(13)中这个的置换转化成
 (15)
(15)
为了考虑较为复杂难于处理的情况,我们构造一个下界和一个上界,然后再一次应用上面的不等式,对于左边则有关系式
 , (16)
, (16)
这里我们假定 是x中的最大的非零元素,使用不等式关系
是x中的最大的非零元素,使用不等式关系 和
和 。对于等式(15)的右边的一个相似的处理即可以导出
。对于等式(15)的右边的一个相似的处理即可以导出
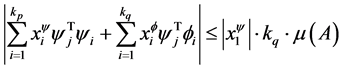 , (17)
, (17)
将这两个边界插入到(15)中的不等式我们得到不等式关系:
 , (18)
, (18)
当我们假设 包含了最大的非零元素后,对于相反的情况一个平行的要求
包含了最大的非零元素后,对于相反的情况一个平行的要求 也是必要的。
也是必要的。
现在我们考虑上边提到的要求($),然后根据同样的处理,左边的下界保持不变,然而右边的上界变为如下不等式:
 , (19)
, (19)
且处处要求如下关系成立:
 . (20)
. (20)
紧接着,下一步就是对于误差 的一个更新。在这个更新中,我们减掉了乘以列
的一个更新。在这个更新中,我们减掉了乘以列 的系数,因此新的误差仍然是一个不超过
的系数,因此新的误差仍然是一个不超过 个非零值的线性组合,并且有着同样的支撑
个非零值的线性组合,并且有着同样的支撑 和
和 。所以,如果在
。所以,如果在 的条件能达成一致,使用上述步骤中同样的设定则能够保证这些算法再一次从真实的支撑中找到一个指标。在经过准确的
的条件能达成一致,使用上述步骤中同样的设定则能够保证这些算法再一次从真实的支撑中找到一个指标。在经过准确的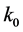 次这样的迭代之后,这个误差变为零并且这个算法终止,保证了在恢复正确的解x中的所有的这些算法的成功。
次这样的迭代之后,这个误差变为零并且这个算法终止,保证了在恢复正确的解x中的所有的这些算法的成功。
2) 贪婪算法
假设矩阵A有 ,并且此时假定优化问题(P0问题)有最优解1,所以b是矩阵A的一些列向量的线性组合,并且这个解也是我们的唯一解。可以通过对矩阵A的每一列进行m次测试来确定这
,并且此时假定优化问题(P0问题)有最优解1,所以b是矩阵A的一些列向量的线性组合,并且这个解也是我们的唯一解。可以通过对矩阵A的每一列进行m次测试来确定这
个列,则第j次测试可以通过将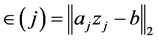 减小到最少加以处理,并导出
减小到最少加以处理,并导出 ,此时这个误差即为如下描述形式:
,此时这个误差即为如下描述形式:
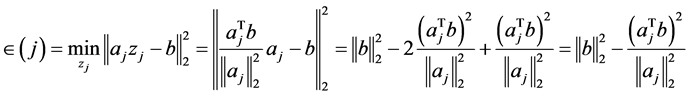 .
.
如果这个误差是0,我们就找到了适当的解。因此这个测试将要做的仅仅是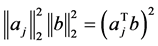 (这个将等价于说Cauchy-Schwartz不等式将满足等式条件),此时意味着b和
(这个将等价于说Cauchy-Schwartz不等式将满足等式条件),此时意味着b和 是平行的。同理,假设矩阵A有
是平行的。同理,假设矩阵A有 ,并且此时假定这个优化问题有最优解值
,并且此时假定这个优化问题有最优解值 。那么b就是矩阵A的至多
。那么b就是矩阵A的至多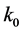 列的线性组合。以此类推,我们计算矩阵A的
列的线性组合。以此类推,我们计算矩阵A的 列的所有的
列的所有的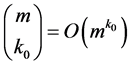 子集合,并且相互测试。贪婪策
子集合,并且相互测试。贪婪策
略放弃了穷举搜索支持一系列的局部最佳的更新。从 开始,它通过维持了一套活跃的列向量(最初是空的)并且每一个阶段都通过一个额外的列来进行扩展迭代设计了一个k条的近似值
开始,它通过维持了一套活跃的列向量(最初是空的)并且每一个阶段都通过一个额外的列来进行扩展迭代设计了一个k条的近似值 。在每一步的列的选择上都从当前活跃的列中接近b的值中最大的减少了残留
。在每一步的列的选择上都从当前活跃的列中接近b的值中最大的减少了残留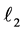 误差。在构造一个包括新的列的近似值之后,残留
误差。在构造一个包括新的列的近似值之后,残留 误差是可以估计出来的,直到某时刻它达到了事前给定的阈值,此时算法终止。
误差是可以估计出来的,直到某时刻它达到了事前给定的阈值,此时算法终止。
关于贪婪算法的具体实现方法有很多种,主要有正交贪婪算法 [85] 、规整化正交贪婪算法 [86] 、分段正交贪婪算法 [87] 和梯度贪婪算法 [88] 等。贪婪算法的基本思想:每次搜索和信号最相关的基函数,然后把信号中所包含最多基函数对应的分量去除,一直到信号被基函数成分去除完毕为止。
3) 熵优化方法
熵最小优化算法类似于最小0-范数算法,是为了解决Pe问题而进行的优化,是NP问题,无法有效地求解,因此文献 [58] 提出了一种熵贪婪思想,即每次求取最大熵对应的系数,依次从大到小抽取信号直至满足给定阈值,算法终止。
首先,假定:
 and
and .
.
在步骤n,通过下式优化,选取 :
:
 . (21)
. (21)
计算一个近似量和一个表示系数:
 .(22)
.(22)
重复上述步骤直到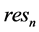 满足事前给定阈值
满足事前给定阈值 ,这里
,这里 为给定阈值。
为给定阈值。
此为还有其他多种方法可以解决上述三大类问题。极小化1-范数的方法能够有效解决压缩感知中的恢复问题,但是当结合其它的一些先验知识后,该问题可以被更加有效地解决,比如贝叶斯压缩感知方法 [91] [92] 和基于模型的压缩感知方法 [93] 。Ji等人提出的BCS借助传统的贝叶斯方法和机器学习中的主动学习方法,通过将关于稀疏性的先验信息用垂直先验分布来建模,提出了自适应的感知方法以及相应的恢复方法。而Baraniuk等人提出的针对基于模型可压缩信号的压缩感知方法中利用小波树模型和块稀疏模型,仅需要与稀疏程度相当的测度数即可实现信号的鲁棒性恢复。制约0-范数问题(P0问题)求解的根源在于矢量的0-范数是该矢量的不连续函数,于是Mohimani等人提出利用高斯函数族对这个不连续函数进行近似,并利用连续函数的最小化算法(如最速下降法)对其最小化,从而得到最小 范数解,即平滑
范数解,即平滑 算法 [89] [90] 。
算法 [89] [90] 。
4) RIP条件
在针对上述优化过程中,对限制条件中矩阵A有哪些要求呢?或者说,矩阵A满足哪些条件则会保证我们获得可靠、稳定的优化解呢?为此,Candes 和Tao提出了受限等距性质(Restricted isometry property, RIP) [81] ,对于矩阵A的特性提出了要求,满足该要求则使我们的优化结果分析变得更为简单。
定义1:对于一个有 标准化的列的大小为
标准化的列的大小为 (
( )的矩阵A,以及一个整数标量
)的矩阵A,以及一个整数标量 满足
满足 ,假定包含A中的s列的子矩阵为
,假定包含A中的s列的子矩阵为 ,且把
,且把 (
( )定义为最小的量,以致
)定义为最小的量,以致
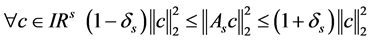 (23)
(23)
对于s列的任何选择都是有效的。那么A就是称为在常量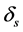 下有一个s-RIP。
下有一个s-RIP。
也就是说,如果A中的s列的任何子集合都是一个正交变换,那么信息总是没有能量变化的。清晰的,这个定义仅仅是对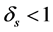 的时候是有益的。RIP常量的上述界限是很容易通过以下公式看出来
的时候是有益的。RIP常量的上述界限是很容易通过以下公式看出来
 . (24)
. (24)
在以上的叙述中我们用了格拉姆矩阵中的最小量的结构,在主对角线上都是1在非主对角线上的元素都是通过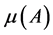 来限制的。对于长度为s的向量c,我们也使用了正常的等值不等式
来限制的。对于长度为s的向量c,我们也使用了正常的等值不等式 。这个下界可以同样被确定为
。这个下界可以同样被确定为
 . (25)
. (25)
这里我们再一次使用正常的等值不等式 。
。
3.3. 矩阵稀疏及秩最小化问题
与压缩传感紧密相关的一个问题是矩阵秩最小化问题。低秩矩阵模型在信号处理等领域具有广泛的应用,例如系统辨识与控制、欧氏空间嵌入和协同滤波等,这往往涉及到仿射矩阵秩最小化的问题 [94] - [96] 。另一方面,低秩矩阵涉及到核范数,即奇异值最稀疏问题,所以矩阵秩最小化问题是稀疏表示中的另外一大类。其数学模型如下:
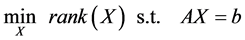 . (26)
. (26)
矩阵秩最小化的一个经典例子就是矩阵填充中的Netflix问题。Netflix公司是一个影碟租赁公司,该公司让用户在观看影碟后对电影打分,然后该公司会根据用户的打分推测出用户对于影片的喜好,从而给用户推荐喜爱的影碟。如果将每一名对电影打分的用户都看成矩阵的一行,再把每一部被评分的电影看成矩阵的一列,用户对于电影的打分看成是矩阵的元素。在现实生活中,一个用户看过的电影总是有限的,因此评分矩阵中仅有少量的元素是已知的。该公司要预测用户对于影片的喜好,就是要通过这些已知的少量的矩阵元素,推测出空白的矩阵元素,这就是一个典型的矩阵填充问题。另外,由于影响用户对于影片的喜好的因素往往只有少数几个,因此这个矩阵将是一个低秩矩阵。曾经Netflix公司还举办过一个比赛,参赛队伍根据Netflix公司提供的用户对于影片的打分数据对用户喜好进行预测,设计新的预测方法,并与Netflix公司自己的预测软件结果进行对比,其中能将预测准确度提高10%的队伍将获得100万美元的大奖。
某个矩阵如果只有部分观测元素(可能占该矩阵元素很低的比例),我们要推测出其他没有观测到的元素,这便是矩阵填充问题。如果对于矩阵没有任何条件限制,矩阵填充问题的解无穷多,但是在实际很多时候我们遇到的矩阵都是低秩矩阵或者渐进低秩矩阵。研究表明 [95] - [100] ,可以通过合适的方法准确恢复出原来的矩阵,矩阵填充问题总结起来就是求解核范数最小化问题 [96] ,现在求解核范数最小化问题已经有了一些成熟的算法,但是目前这些算法的复杂度一般都很高,处理高维矩阵的填充问题会花费大量时间,也正因此,快速高效的矩阵填充算法也是矩阵填充问题的一个研究热点。矩阵填充目前已有不少算法,最经典的当属由Cai等人提出的SVT算法 [97] ,该算法受到压缩感知中Bregman迭代算法的启发,算法在迭代过程中对矩阵进行了奇异值分解,然后将较小的奇异值设置为0,生成新的矩阵进行反复迭代,此算法运行速度很快,对于高维低秩矩阵的回填效果很好。另外还有Ma等人提出的FPCA算法 [99] ,该算法也用到了矩阵的奇异值分解,并且在算法迭代过程中进行不动点连续处理。该算法不仅对于低秩矩阵的恢复效果很好,对于秩适中的矩阵也有较好的恢复效果。在这之后,又陆续出现了很多关于矩阵填充的快速高效算法。目前矩阵填充问题与算法的研究已经取得了极大的进展,但是理论的不成熟导致仍然存在很多问题,例如一些实际问题中需要填充的低秩矩阵,其核范数是固定的,此时应用核范数最小化方法求解显然没有意义,对于这些问题,需要提出新的算法。本文将给出Cai等人提出的SVT算法,其基本思路如下:
对于给定的矩阵X,矩阵部分数据已知,即下面优化问题即是矩阵填充的数学模型:
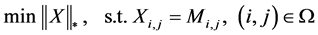 , (27)
, (27)
如果矩阵中数据采样对于给定的某个常数C满足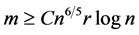 ,上式就会以较高的概率(
,上式就会以较高的概率( )恢复出矩阵缺失元素。这里
)恢复出矩阵缺失元素。这里 表示的是矩阵的核范数,即所有奇异值的和,
表示的是矩阵的核范数,即所有奇异值的和, 为矩阵的秩,
为矩阵的秩,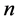 为矩阵行数和列数中的最小值,
为矩阵行数和列数中的最小值, 为矩阵中已知数据个数。由于求解(27)较为困难,上式可以松弛成如下优化问题:
为矩阵中已知数据个数。由于求解(27)较为困难,上式可以松弛成如下优化问题:
 . (28)
. (28)
进一步,Cai等人把限制条件进行了改进 [97] ,不是直接相等约束,而是投影(投影算子设为 )后具有相同的数值(即改为投影约束),即:
)后具有相同的数值(即改为投影约束),即:
 . (29)
. (29)
因此,可以通过迭代优化计算方法(30)直到达到某个停止条件,获得最终的优化矩阵X:
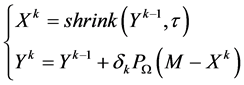 , (30)
, (30)
其中,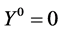 ,
, 为一个非线性软阈值函数,阈值为
为一个非线性软阈值函数,阈值为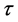 ,
, 为k步相应的步长。这里使用了两个重要的特性:稀疏性和低秩性。矩阵在迭代的过程中一直保持着稀疏性,同时矩阵必须是低秩的,否则该方法将失效。
为k步相应的步长。这里使用了两个重要的特性:稀疏性和低秩性。矩阵在迭代的过程中一直保持着稀疏性,同时矩阵必须是低秩的,否则该方法将失效。
很显然,矩阵填充问题是一个非适定性的问题。一般而言,如果一个矩阵仅仅由少量的采样元素组成,那么完全重构出原矩阵几乎是不可能的,因为对矩阵未知元素的填充有无限种可能性。如果没有其他约束条件,矩阵填充重构出的矩阵将不是唯一的。但是如果我们事先知道原始矩阵数据满足一定的条件,那么矩阵填充将变得可行,这个关键的条件就是矩阵的低秩性 [95] 。
4. 结论
时频分析广义测不准原理,特别是在分数阶Fourier变换域以及线性正则变换域内的时频分析广义测不准原理已经获得了长足的发展 [15] - [20] [31] - [38] [41] - [53] 。本文对这些广义测不准原理中所涉及到的主要数学问题进行了总结,分析了它们各自的使用方法,并给出了几个简单的示例以示效应。
但是,目前公开发表的时频分析广义测不准原理都主要是针对连续信号的,但离散信号与连续信号有许多不同点。首先,在实际工程应用中离散信号的时间支撑和频率支撑都是有限的,而对于连续信号不成立 [54] - [56] ,因此,广泛应用于连续信号的数学不等式(例如广义Pitt不等式、广义Hausdorff-Young不等式等)及其证明方法(例如基于广义Jensen不等式的凹凸理论)都需要进一步完善。其次,目前离散信号的时间支撑和频率支撑的表述还没有一个被广泛接受的统一定义,理论上尚不完善。还有,广义变换离散计算方法、离散性质等还有待进一步分析 [54] - [56] 。另外,业已证明:在传统域内,高斯信号不再是离散测不准原理等式成立的条件。所以,以上这些问题都是下一步在时频分析广义测不准原理中需要重点研究的对象。
对于稀疏表示广义测不准原理,研究正处于白热化状态,也取得了不少进展,比如已有不少文献中的相关工作就涵盖了当前稀疏表示广义测不准原理的研究成果 [57] - [59] [61] [63] - [70] [72] - [74] [76] [81] [86] 。本文对这些广义测不准原理中所涉及到的主要数学问题也进行了总结,分析了不同的范数、优化算法等,并给出了几个典型的数学应用示例。
然而,尽管前期关于稀疏表示广义测不准原理取得了开创性成果,但这些理论结果大多不具备工程可行性,无法在信号的稀疏表示中进行有效的应用,而且这些成果仅限于稀疏表示的广义Heisenberg测不准原理。Denoho、Elad等人给出的结论都包含了信号的0-范数 [59] [63] [64] ,而0-范数既是分解的结果又是稀疏表示的条件。也就是说,如果得到了信号的0-范数,也就得到了信号稀疏表示,则上述理论条件也就起不到对0-范数求解的指导作用。相反,要验证上述理论条件,必须首先求解“信号的0-范数”。 同样,Patrick以及Yonina的结论也存在类似的问题 [65] - [70] 。所以,这些条件无法应用于工程,尽管它们是充要条件。而且,对于熵测不准原理,目前也还没有公开的报道涉及稀疏分解问题,包括信号唯一最佳稀疏表示条件、最小范数和熵等价条件、工程判据等。因此,关于熵的广义测不准原理的稀疏表示问题有必要开展相关的理论研究,特别是数学问题的理论研究。
基金项目
国家自然科学基金《广义测不准原理理论及其应用研究》(61002052)以及《信号稀疏表示的广义测不准原理研究》(61471412)资助支持。
文章引用
徐冠雷,王孝通,周立佳,邵利民,刘永禄,徐晓刚. 广义测不准原理中的数学问题研究
Study on the Mathematical Problems of Generalized Uncertainty Principles[J]. 应用数学进展, 2016, 05(03): 536-559. http://dx.doi.org/10.12677/AAM.2016.53064
参考文献 (References)
- 1. Heisenberg, W. (1927) Uber den anschaulichen inhalt der quanten theoretischen Kinematik und Mechanik. Zeitschrift für Physik, 43, 172-198. http://dx.doi.org/10.1007/BF01397280
- 2. Heinig, H.P. and Smith, M. (1986) Extensions of the Heisenberg-Weyl Inequality. International Journal of Mathe- matics and Science, 9, 185-192. http://dx.doi.org/10.1155/S0161171286000212
- 3. Selig, K.K. (2002) Uncertainty Principles Revisited. Electronic Transactions on Numerical Analysis, 14, 145-177.
- 4. Folland, G.B. and Sitaram, A. (1997) The Uncertainty Principle: A Mathematical Survey. The Journal of Fourier Analysis and Applications, 3, 207-238. http://dx.doi.org/10.1007/BF02649110
- 5. Hirschman Jr., I.I. (1957) A Note on Entropy. American Journal of Mathematics, 79, 152-156. http://dx.doi.org/10.2307/2372390
- 6. Lohmann, A.W. (1994) Relationships between the Radon-Wigner and Fractional Fourier Transfoms. Journal of the Optical Society of America A, 11, 1398-1401. http://dx.doi.org/10.1364/JOSAA.11.001798
- 7. Majerník, V., Majerníková, E. and Shpyrko, S. (2003) Uncer-tainty Relations Expressed by Shannon-Like Entropies. Central European Journal of Physics, 3, 393-420. http://dx.doi.org/10.2478/bf02475852
- 8. Iwo, B.B. (1985) Entropic Uncertainty Relations in Quantum Me-chanics. In: Accardi, L. and von Waldenfels, W., Eds., Quantum Probability and Applications II, Lecture Notes in Mathematics 1136, Springer, Berlin, 90-103.
- 9. Stankovic, L., Alieva, T. and Bastiaans, M.J. (2003) Time-Frequency Signal Analysis Based on the Windowed Fractional Fourier Transform. Signal Processing, 83, 2459-2468. http://dx.doi.org/10.1016/S0165-1684(03)00197-X
- 10. Cohen, L. (2000) The Uncertainty Principles of Windowed Wave Functions. Optics Communications, 179, 221-229. http://dx.doi.org/10.1016/S0030-4018(00)00454-5
- 11. Beckner, W. (1995) Pitt’s Inequality and the Uncertainty Principle. Proceedings of the American Mathematical Society, 123, 1897-1905. http://dx.doi.org/10.1090/s0002-9939-1995-1254832-9
- 12. Beckner, W. (1975) Inequalities in Fourier Analysis. The Annals of Mathematics, 102, 159-182. http://dx.doi.org/10.2307/1970980
- 13. Cohen, L. (1994) The Uncertainty Principle in Signal Analysis. Proceed-ings of the IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis, IEEE, 182-185.
- 14. Loughlin, P.J. and Cohen, L. (2004) The Uncertainty Principle: Global, Local, or Both? IEEE Transaction on Signal Processing, 52, 1218-1227. http://dx.doi.org/10.1109/TSP.2004.826160
- 15. Ozaktas, H.M. and Aytur, O. (1995) Fractional Fourier Domains. Signal Processing, 46, 119-124. http://dx.doi.org/10.1016/0165-1684(95)00076-P
- 16. Mustard, D. (1991) Uncertainty Principle Invariant under Fractional Fourier Transform. Journal of the Australian Mathematical Society Series B, 33, 180-191. http://dx.doi.org/10.1017/S0334270000006986
- 17. Shinde, S. and Vikram, M.G. (2001) An Uncertainty Principle for Real Signals in the Fractional Fourier Transformdomain. IEEE Transaction on Signal Processing, 49, 2545-2548. http://dx.doi.org/10.1109/78.960402
- 18. Stern, A. (2008) Uncertainty Principles in Linear Canonical Transform Domains and Some of Their Implications in Optics. Journal of the Optical Society of America A, 25, 647-652. http://dx.doi.org/10.1364/JOSAA.25.000647
- 19. Stern, A. (2007) Sampling of Compact Signals in Offset Linear Canonical Transform Domains. Signal, Image and video Processing, 1, 359-367. http://dx.doi.org/10.1007/s11760-007-0029-0
- 20. Aytur, O. and Ozaktas, H.M. (1995) Non-Orthogonal Domains in Phase Space of Quantum Optics and Their Relation to Fractional Fourier Transform. Optics Communications, 120, 166-170. http://dx.doi.org/10.1016/0030-4018(95)00452-E
- 21. Maassen, H. (1988) A Discrete Entropic Uncertainty Rela-tion. In: In: Accardi, L. and von Waldenfels, W., Eds., Quantum Probability and Applications V, Springer-Verlag, New York, 263-266.
- 22. Maassen, H. and Uffink, J.B.M. (1983) Generalized Entropic Uncertainty Relations. Physical Re-view Letters, 60, 1103-1106. http://dx.doi.org/10.1103/PhysRevLett.60.1103
- 23. Amir, D. and Cover, T.M. and Thomas, J.A. (2001) Information Theoretic Inequalities. IEEE Trans Information Theory, 37, 1501-1508.
- 24. Iwo, B.B. (2006) Formulation of the Uncertainty Relations in Terms of the Rényi Entropies. Physical Review A, 74, Article ID: 052101.
- 25. Iwo, B.B. (2006) Rényi Entropy and the Uncertainty Relations. In: Adenier, G., Fuchs, C.A. and Khrennikov, A.Y., Eds., Foundations of Probability and Physics, American Institute of Physics, Melville, 52-62
- 26. Gill, J. (2005) An Entropymeasure of Uncertainty in Vote Choice. Electoral Studies, 1-22.
- 27. Rényi, A. (1976) Some Fundamental Questions of Information Theory. In: Selected Papers of Alfred Renyi, Vol. 2, Akademia Kiado, Budapest, 526-552.
- 28. Rényi, A. (1960) On Measures of Information and Entropy. Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability, 1, 547-561.
- 29. Sharma, K.K. and Joshi, S.D. (2008) Uncertainty Principle for Real Signals in the Linear Canonical Transform Domains. IEEE Transaction on Signal Processing, 56, 2677-2683. http://dx.doi.org/10.1109/TSP.2008.917384
- 30. Shannon, C.E. (1948) A Mathemat-ical Theory of Communication. The Bell System Technical Journal, 27, 379-656. http://dx.doi.org/10.1002/j.1538-7305.1948.tb01338.x
- 31. Wódkiewicz, K. (1984) Operational Approach to Phase-Space Measurements in Quantum Mechanics. Physical Review Letters, 52, 1064-1067. http://dx.doi.org/10.1103/PhysRevLett.52.1064
- 32. Xu, G., Wang, X. and Xu, X. (2009) Three Cases of Uncer-tainty Principle for Real Signals in Linear Canonical Transform Domain. IET Signal Processing, 3, 85-92. http://dx.doi.org/10.1049/iet-spr:20080019
- 33. Xu, G., Wang, X. and Xu, X. (2009) Uncertainty Inequalities for Linear Canonical Transform. IET Signal Processing, 3, 392-402. http://dx.doi.org/10.1049/iet-spr.2008.0102
- 34. Xu, G., Wang, X. and Xu, X. (2009) The Logarithmic, Heisen-berg’s and Windowed Uncertainty Principles in Fractional Fourier Transform Domains. Signal Processing, 89, 339-343. http://dx.doi.org/10.1016/j.sigpro.2008.09.002
- 35. Xu, G., Wang, X. and Xu, X. (2009) The Entropic Uncertainty Principle in Fractional Fourier Transform Domains. Signal Processing, 89, 2692-2697. http://dx.doi.org/10.1016/j.sigpro.2009.05.014
- 36. Xu, G., Wang, X. and Xu, X. (2010) Novel Uncertainty Rela-tions in Fractional Fourier Transform Domain for Real Signals. Chinese Physics B, 19, 294-302.
- 37. Xu, G., Wang, X. and Xu, X. (2009) New Inequalities and Uncertainty Relations on Linear Canonical Transform Revisit. EURASIP Journal on Advances in Signal Processing, 1-17.
- 38. Zhao, J., Tao, R., Li, Y. and Wang, Y. (2009) Uncertainty Prin-ciples for Linear Canonical Transform. IEEE Transactions on Signal Processing, 57, 2856-2858. http://dx.doi.org/10.1109/TSP.2009.2020039
- 39. Xia, X.G. (1996) On Bandlimited Signals with Fractional Fourier Transform. IEEE Signal Processing Letter, 3, 72-74. http://dx.doi.org/10.1109/97.481159
- 40. Wilk, G. and Włodarczyk, Z. (2009) Uncertainty Relations in Terms of the Tsallis Entropy. Physical Review A, 79, Article ID: 062108. http://dx.doi.org/10.1103/PhysRevA.79.062108
- 41. Amir, D., Cover, T.M. and Thomas, J.A. (2001) Information Theoretic Inequalities, IEEE Trans Information Theory, 37, 1501-1508.
- 42. Xu, G., Wang, X., Zhou, L., Shao, L. and Xu, X. (2013) Discrete Entropic Uncertainty Relations Associated with FRFT. Journal of Signal and Information Processing, 4, 120-124. http://dx.doi.org/10.4236/jsip.2013.43B021
- 43. Xu, X.G., Wang, X.T., Wang, L., Liu, B., Su, S. and Xu, X. (2013) Generalized Uncertainty Principles Associated with Hilbert Transform. Signal, Image and Video Processing, 8, 279-285. http://dx.doi.org/10.1007/s11760-013-0547-x
- 44. Xu, G., Wang, X. and Zhou, L. (2013) Generalized Uncertainty Relations on Fractional Fourier Transform for Discrete Signals and Filtering of LFM Signals. Journal of Signal and Information Processing, 4, 274-281. http://dx.doi.org/10.4236/jsip.2013.43035
- 45. Tao, R., Li, Y. and Wang, Y. (2009) Short-Time Fractional Fourier Transform and Its Applications. IEEE Transaction on Signal Processing, 58, 2568-2580. http://dx.doi.org/10.1109/TSP.2009.2028095
- 46. Ozaktas, H.M., Kutay, M.A. and Zalevsky, Z. (2000) The Fractional Fourier Transform with Applications in Optics and Signal Processing. John Wiley & Sons, New York.
- 47. Pei, S.C., Yeh, M.H. and Luo, T.L. (1999) Fractional Fourier Series Expansion for Finite Signals and Dual Extension to Discrete-Time Fractional Fourier Transform. IEEE Transaction on Signal Processing, 47, 2883-2888. http://dx.doi.org/10.1109/78.790671
- 48. Xu, G., Wang, X. and Xu, X. (2010) On Uncertainty Principle for the Linear Canonical Transform of Complex Signals. IEEE Transactions on Signal Processing, 58, 4916-4918. http://dx.doi.org/10.1109/TSP.2010.2050201
- 49. Almeida, L.B. (1994) The Fractional Fourier Transform and Time-Frequency Representations. IEEE Transaction on Signal Processing, 42, 3084-3091. http://dx.doi.org/10.1109/78.330368
- 50. Dang, P., Deng, G.-T. and Qian, T. (2013) A Tighter Uncertainty Prin-ciple for Linear Canonical Transform in Terms of Phase Derivative. IEEE Transactions on Signal Processing, 61, 5153-5164. http://dx.doi.org/10.1109/TSP.2013.2273440
- 51. Dang, P., Deng, G.-T. and Qian, T. (2013) A Sharper Uncer-tainty Principle. Journal of Functional Analysis, 265, 2239- 2266. http://dx.doi.org/10.1016/j.jfa.2013.07.023
- 52. Shi, J., Liu, X. and Zhang, N. (2012) On Uncertainty Principle for Signal Concentrations with Fractional Fourier Transform. Signal Processing, 92, 2830-2836. http://dx.doi.org/10.1016/j.sigpro.2012.04.008
- 53. Pei, S.-C. and Ding, J.-J. (2009) Uncertainty Principle of the 2-D Affine Generalized Fractional Fourier Transform. Proceedings of 2009 APSIPA Annual Summit and Conference, Sapporo, October 4-7, 2009, 414-417.
- 54. 陶然, 邓兵, 王越. 分数阶Fourier变换及其应用[M]. 北京: 北京清华大学出版社, 2009.
- 55. 冉启文, 谭立英. 分数傅里叶光学导论[M]. 北京: 北京科学出版社, 2004.
- 56. 张贤达, 保铮. 非平稳信号分析与处理[M]. 北京: 北京国防工业出版社, 1998.
- 57. Xu, G., Wang, X., Zhou, L. and Xu, X. (2013) New Inequalities on Sparse Representation in Pairs of Bases. IET Signal Processing, 7, 674-683. http://dx.doi.org/10.1049/iet-spr.2012.0365
- 58. Xu, G., Wang, X., Xu, X. and Zhou, L. (2016) Entropic Uncer-tainty Inequalities on Sparse Representation. IET Signal Processing, 10, 413-421. http://dx.doi.org/10.1049/iet-spr.2014.0072
- 59. Donoho, D. and Stark, P. (1989) Uncertainty Principles and Signal Recovery. SIAM Journal on Applied Mathematics, 49, 906-931. http://dx.doi.org/10.1137/0149053
- 60. Donoho, D. (2006) Compressed Sensing. IEEE Transactions on Informa-tion Theory, 52, 1289-1306. http://dx.doi.org/10.1109/TIT.2006.871582
- 61. Candès, E. and Romberg, J. (2007) Sparsity and Incoherence in Compressive Sampling. Inverse Problems, 23, 969-985. http://dx.doi.org/10.1088/0266-5611/23/3/008
- 62. Candès, E.J. and Wakin, M.B. (2008) An Introduction to Compressive Sampling. IEEE Signal Processing Magazine, 25, 21-30. http://dx.doi.org/10.1109/MSP.2007.914731
- 63. Donoho, D.L. and Huo, X. (2001) Uncertainty Principles and Ideal Atomic Decomposition. IEEE Transactions on Information Theory, 47, 2845-2862. http://dx.doi.org/10.1109/18.959265
- 64. Elad, M. and Bruckstein, A.M. (2002) A Generalized Uncertainty Prin-ciple and Sparse Representation in Pairs of Bases. IEEE Transactions on Information Theory, 48, 2558-2567. http://dx.doi.org/10.1109/TIT.2002.801410
- 65. Feuer, A. and Nemirovski, A. (2003) On Sparse Representation in Pairs of Bases. IEEE Transactions on Information Theory, 49, 1579-1581. http://dx.doi.org/10.1109/TIT.2003.811926
- 66. Gribonval, R. and Nielsen, M. (2003) Sparse Representations in Unions of Bases. IEEE Transactions on Information Theory, 49, 3320-3325. http://dx.doi.org/10.1109/TIT.2003.820031
- 67. Li, Y. and Amari, S. (2010) Two Conditions for Equivalence of 0-Norm Solution and 1-Norm Solution in Sparse Representation. IEEE Transactions on Neural Networks, 21, 1189-1196. http://dx.doi.org/10.1109/TNN.2010.2049370
- 68. Fuchs, J.J. (2004) On Sparse Representations in Arbitrary Redundant Bases. IEEE Transactions on Information Theory, 50, 1341-1344. http://dx.doi.org/10.1109/TIT.2004.828141
- 69. Lyubarskii, Y. and Vershynin, R. (2010) Uncertainty Principles and Vector Quantization. IEEE Transactions on Information Theory, 56, 3491-3501. http://dx.doi.org/10.1109/TIT.2010.2048458
- 70. Patrick, K., Giuseppe, D. and Helmut, B. (2012) Uncertainty Relations and Sparse Signal Recovery for Pairs of General Signal Sets. IEEE Transactions on Information Theory, 58, 263-277. http://dx.doi.org/10.1109/TIT.2011.2167215
- 71. Benjamin, R. and Bruno, T. (2013) Refined Support and Entropic Uncertainty Inequalities. IEEE Transactions on Information Theory, 59, 4272-4279. http://dx.doi.org/10.1109/TIT.2013.2249655
- 72. Goha, S.S. and Goodmanb, T.N.T. (2006) Uncertainty Principles in Banach Spaces and Signal Recovery. Journal of Approximation Theory, 143, 26-35. http://dx.doi.org/10.1016/j.jat.2006.03.009
- 73. Eldar, Y.C. (2009) Uncertainty Relations for Shift-Invariant Analog Signals. IEEE Transactions on Information Theory, 55, 5742-5757. http://dx.doi.org/10.1109/TIT.2009.2032711
- 74. Agaskar, A. and Lu, Y. (2013) A Spectral Graph Uncertainty Principle. IEEE Transactions on Information Theory, 59, 4338-4356. http://dx.doi.org/10.1109/TIT.2013.2252233
- 75. Candés, E.J. and Tao, T. (2005) Decoding by Linear Program-ming. IEEE Transactions on Information Theory, 51, 4203-4215. http://dx.doi.org/10.1109/TIT.2005.858979
- 76. Chen, S., Donoho, D.L. and Saunders, M.A. (1998) Atomic De-composition by Basis Pursuit. SIAM Journal on Scientific Computing, 20, 33-61. http://dx.doi.org/10.1137/S1064827596304010
- 77. Candès, E., Romberg, J. and Tao, T. (2005) Stable Signal Recovery from Incomplete and Inaccurate Measurements. Communications on Pure and Applied Mathematics, 59, 1207-1223. http://dx.doi.org/10.1002/cpa.20124
- 78. Davis, G., Mallat, S. and Avellaneda, M. (1997) Adaptive Greedy Approximations in Constructive Approximation. Springer-Verlag, New York, Vol. 13, 57-98.
- 79. Mallat, S. and Zhang, Z. (1993) Matching Pursuits with Time-Frequency Dictionaries. IEEE Transactions on Signal Processing, 41, 3397-3415. http://dx.doi.org/10.1109/78.258082
- 80. Pati, Y.C., Rezaiifar, R. and Krishnaprasad, P.S. (1993) Orthogonal Matching Pursuit: Recursive Function Approximation with Applications to Wavelet Decomposition. Pro-ceeding of 27th Annual Asilomar Conference on Signals Systems and Computers, Asilomar, 1-3 November 2009, 40-44. http://dx.doi.org/10.1109/ACSSC.1993.342465
- 81. Candès, E., Romberg, J. and Tao, T. (2006) Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information. IEEE Transactions on Information Theory, 52, 489-509. http://dx.doi.org/10.1109/TIT.2005.862083
- 82. Tropp, J.A. (2004) Greed Is Good. IEEE Transactions on In-formation Theory, 50, 2231-2242. http://dx.doi.org/10.1109/TIT.2004.834793
- 83. Cevher, V. and Krause, A. (2011) Greedy Dictionary Selection for Sparse Representation. IEEE Journal of Selected Topics in Signal Processing, 5, 979-2011. http://dx.doi.org/10.1109/JSTSP.2011.2161862
- 84. 张贤达. 矩阵分析及应用[M]. 第二版. 北京: 清华大学出版社, 2015.
- 85. Tropp, J.A. and Gilbert, A.C. (2007) Signal Recovery from Random Measurements via Orthogonal Matching Pursuit. IEEE Transactions on Information Theory, 53, 4655-4666. http://dx.doi.org/10.1109/TIT.2007.909108
- 86. Needell, D. and Vershynin, R. (2007) Uniform Uncertainty Principle and Signal Recovery via Regularized Orthogonal Matching Pursuit. Foundations of Computational Mathe-matics, 9, 317-334. http://dx.doi.org/10.1007/s10208-008-9031-3
- 87. Donoho, D.L., et al. (2006) Sparse Solution of Underdeter-mined Linear Equations by Stagewise Orthogonal Matching Pursuit. Department of Statistics, Stanford University, Stanford, Technical Report 2006-02, 200.
- 88. Blumensath, T. and Davies, M.E. (2008) Gradient Pursuits. IEEE Transactions on Signal Processing, 56, 2370-2382. http://dx.doi.org/10.1109/TSP.2007.916124
- 89. Mohimani, G.H., Babaie-Zadeh, M. and Jutten, C. () Com-plex-Valued Sparse Representation Based on Smoothed l0 norm. IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, March 2008, 3881- 3884.
- 90. Mohimani, H., Babaie-Zadeh, M. and Jutten, C. (2009) A Fast Approach for Overcomplete Sparse Decomposition Based on Smoothed l0 Norm. IEEE Transaction on Signal Processing, 57, 289-301. http://dx.doi.org/10.1109/TSP.2008.2007606
- 91. Ji, S. and Carin, L. (2007) Bayesian Compressive Sensing and Projection Optimization. Proceedings of the 24th International Conference on Machine Learning (ICML). Corvallis, 20-24 June 2007, 377-384. http://dx.doi.org/10.1145/1273496.1273544
- 92. Ji, S., et al. (2008) Bayesian Compressive Sensing. IEEE Transactions on Signal Processing, 56, 2346-2356. http://dx.doi.org/10.1109/TSP.2007.914345
- 93. Baraniuk, R., Cevher, V., Duarte, M.F. and Hegde, C. (2010) Model Based Compressive Sensing. IEEE Transactions on Information Theory, 56, 1982-2001. http://dx.doi.org/10.1109/TIT.2010.2040894
- 94. Natarajan, B.K. (1995) Sparse Approximate Solutions to Linear Systems. SIAM Journal of Computing, 24, 227-234. http://dx.doi.org/10.1137/S0097539792240406
- 95. Candes, E.J. and Tao, T. (2009) The Power of Convex Re-laxation: Near-Optimal Matrix Completion. IEEE Transactions on Information Theory, 56, 2053-2080. http://dx.doi.org/10.1109/TIT.2010.2044061
- 96. Chandrasekaran, V., Sanghavi, S., Parrilo, P.A. and Willsky, A.S. (2011) Rank-Sparsity Incoherence for Matrix Decomposition. SIAM Journal on Optimization, 21, 572-596. http://dx.doi.org/10.1137/090761793
- 97. Cai, J.F., Candes, E.J. and Shen, Z.W. (2010) A Singular Value Thre-sholding Algorithm for Matrix Completion. SIAM Journal on Optimizatinon, 20, 1956-1982. http://dx.doi.org/10.1137/080738970
- 98. Ma, S., Goldfarb, D. and Chen, L. (2008) Fixed Point and Bregman Iterative Methods for Matrix Rank Minimization. Technical Report.
- 99. Keshavan, R.H., Montanari, A. and Sewoong, O.H. (2010) Matrix Completion from a Few Entries. IEEE Transactions on Information Theory, 56, 2980-2998. http://dx.doi.org/10.1109/TIT.2010.2046205
- 100. Benjamin, R. (2009) A Simpler Approach to Matrix Completion. Journal of Machine Learning Research, 12, 3413- 3430.a
