Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:19123,7
pages
10.12677/AAM.2016.54090
A Scaling Law of the SIR Outbreak Prevalence in Heterogeneous Medias
Weihua Peng, Jiazeng Wang*
Department of Mathematics, School of Science, Beijing Technology and Business University, Beijing

Received: Nov. 10th, 2016; accepted: Nov. 25th, 2016; published: Nov. 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we study the scaling law of the outbreak prevalence of susceptible-infectious-re- moved epidemic on the transmissibility. The scale of prevalence is calculated by bond percolation method, which is got through a self-consistent equation. Near the threshold region, we find that the scaling law coefficients of different media structures, which were represented by degree distributions, are equal to unity if the media is not so heterogeneous. For scale free networks, we find that when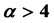 , the scaling law coefficient is 1; when
, the scaling law coefficient is 1; when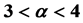 , the scaling law coefficient is
, the scaling law coefficient is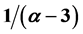 ; when
; when , the corresponding scaling law is
, the corresponding scaling law is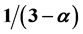 , which are bigger than one and depending on the parameter
, which are bigger than one and depending on the parameter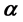 .
.
Keywords:Susceptible-Infectious-Removed, Bond Percolation, Probability Generating Function, Scaling Law

异质群体中SIR型传染病爆发流行的标度律
彭为花,王家赠*
北京工商大学,理学院数学系,北京

收稿日期:2016年11月10日;录用日期:2016年11月25日;发布日期:2016年11月30日

摘 要
本文主要研究异质群体中SIR型传染病的爆发流行规模对于传播速率的标度律。这里的标度律计算是基于键逾渗的方法,它是通过一个自组织方程得到的。在爆发阈值附近,如果底层结构(用度分布来刻画)不是非常异质的话,不同底层结构下的标度律系数是等于1的。但是,对于无标度的网络,在 时,此时的标度律系数也是1;但当
时,此时的标度律系数也是1;但当 和
和 时,标度律系数是大于1的且依赖于参数
时,标度律系数是大于1的且依赖于参数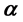 的取值,即
的取值,即 。
。
关键词 :SIR型传染病,键逾渗,概率母函数,标度律

1. 引言
寄主型传染病受到多种异质性因素的影响,如遗传、年龄、空间等等 [1] [2] 。对于像性传播疾病这样的直接性的传染病来讲,寄主群体的性活跃度(性伴侣的个数)是影响其传播的主要的异质因素 [1] [3] 。
从Lajmanovich和Yorke的一篇会议论文开始 [4] ,学者们建立了许多数学模型来研究性活跃度的异质性对于传染病传播的影响 [5] 。近来,用网络的拓扑结构描述传染病传播的数学方法很是流行,具体来说就是用网络中的节点表示个体,用边来表示个体之间的接触。有趣的是,许多刻画性传播疾病的社交网络都是服从幂律分布: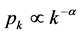 [6] 。按照网络表示论,不同个体性活跃度的异质性可以用寄主群体的度分布来刻画 [7] 。
[6] 。按照网络表示论,不同个体性活跃度的异质性可以用寄主群体的度分布来刻画 [7] 。
众所周知,包括HIV在内的一些性传播疾病属于易感–感染–移除(SIR)型传染病,以往大家关注的焦点是该型传染病的阈值现象 [8] 。但逐渐地有人认识到SIR型传染病可以映射到无穷维的键逾渗问题上来研究 [9] [10] 。相应的,传染病模型中的一些量可以用逾渗理论中的量来代替,如传播强度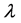 可以用键占据率
可以用键占据率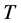 来替换,用逾渗阈值
来替换,用逾渗阈值 来代替爆发阈值
来代替爆发阈值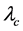 。
。
另外,Newman等人利用概率母函数的重整化方法 [11] ,得到了含有传播率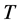 的自组织方程。这一方法是求解Golton-Waterson分支树阈值问题的著名方法。正如Durrett [12] 所指出的,该方法用在随机图中并不是严格的,其中的问题是当传染病速率在阈值之上时,传染病的传播就会产生回路,即:被传染的个体会再次被传染。此时再用分支树模型会有误差,但他指出这种误差是很小的,所以经过一个小的变动,该自组织方程仍然适用 [12] 。
的自组织方程。这一方法是求解Golton-Waterson分支树阈值问题的著名方法。正如Durrett [12] 所指出的,该方法用在随机图中并不是严格的,其中的问题是当传染病速率在阈值之上时,传染病的传播就会产生回路,即:被传染的个体会再次被传染。此时再用分支树模型会有误差,但他指出这种误差是很小的,所以经过一个小的变动,该自组织方程仍然适用 [12] 。
基于上述结果,本文研究当 时,即:
时,即: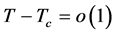 时的标度律问题。并发现在不同的底层结构下,如同质结构、泊松分布、几何分布等,SIR型传染病爆发流行的标度律系数都是1,而对于无标度网络,它的标度律系数是依赖于参数
时的标度律问题。并发现在不同的底层结构下,如同质结构、泊松分布、几何分布等,SIR型传染病爆发流行的标度律系数都是1,而对于无标度网络,它的标度律系数是依赖于参数 的。
的。
本文的框架如下:第二节我们介绍SIR型传染病的键逾渗理论;第三部分给出不同情形下的爆发流行的标度律。
2. 具有任意度分布的随机图的键逾渗理论
在文献 [11] 中,Newman把概率母函数与键逾渗理论相结合,来研究具有任意度分布的随机图上的SIR型传染病模型。首先,从节点出发,节点的度分布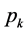 (任选一个节点度
(任选一个节点度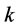 为的概率)的概率母函数定义如下:
为的概率)的概率母函数定义如下:
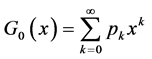 (2.1)
(2.1)
如果从边出发,即:从网络中任选一条边并沿着该边到达的节点,此时该节点除了原始入边之外,剩余边的总数叫做该节点的超出度,其相应度分布的母函数为:
 (2.2)
(2.2)
当传染病在网络上传播时,它并不是通过所有的边进行传播而是以平均传播速率 在某些边上进行传播,显然
在某些边上进行传播,显然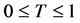 。在流行病中边被传染了又叫做被占领,正如Newman所说,网络中一旦有某些边被占领,那么原来网络的结构就会发生变化。此时要想得到传染病的爆发流行(流行病中感染人数的比例),就必须考虑节点的被占领的边的分布,并且他用
。在流行病中边被传染了又叫做被占领,正如Newman所说,网络中一旦有某些边被占领,那么原来网络的结构就会发生变化。此时要想得到传染病的爆发流行(流行病中感染人数的比例),就必须考虑节点的被占领的边的分布,并且他用 表示该分布的母函数,另外还给出了
表示该分布的母函数,另外还给出了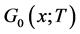 与
与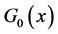 之间的关系:
之间的关系:
 (2.3)
(2.3)
类似的,定义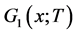 为节点的超出度中被占领边的分布(任选一条边所到达的节点的剩余边中被占领的边数的分布)的母函数,它与
为节点的超出度中被占领边的分布(任选一条边所到达的节点的剩余边中被占领的边数的分布)的母函数,它与 之间的关系如下:
之间的关系如下:
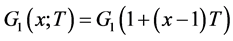 (2.4)
(2.4)
设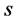 表示的是从节点出发(随机选择一个顶点)得到的小规模爆发的传染病中个体的数目,并令
表示的是从节点出发(随机选择一个顶点)得到的小规模爆发的传染病中个体的数目,并令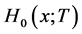 为爆发规模分布的母函数,它可以表示为:
为爆发规模分布的母函数,它可以表示为:
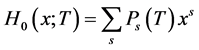 (2.5)
(2.5)
其中 表示的是由单个感染个体以平均传播速率
表示的是由单个感染个体以平均传播速率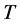 引发的爆发规模为
引发的爆发规模为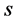 的传染病的概率。令
的传染病的概率。令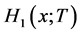 为任选一条边,并沿着它到达的节点与规模为
为任选一条边,并沿着它到达的节点与规模为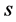 的簇连接的概率的母函数,或者按照分支过程的观点,它表示的是第0代的一个感染个体,经过几轮感染之后所有的感染个体的总数目的母函数。关于
的簇连接的概率的母函数,或者按照分支过程的观点,它表示的是第0代的一个感染个体,经过几轮感染之后所有的感染个体的总数目的母函数。关于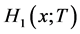 的Dyson方程的自组织形式如下 [11] :
的Dyson方程的自组织形式如下 [11] :
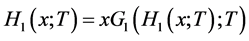 (2.6)
(2.6)
该方程可以简单粗略的解释为:随机选择一条边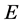 所得到的大集团的规模等于,沿着边
所得到的大集团的规模等于,沿着边 到达节点
到达节点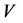 所引发的通过被占领的边连接的所有簇(小集团)规模之后再加上节点
所引发的通过被占领的边连接的所有簇(小集团)规模之后再加上节点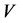 本身 [10] 。类似的,随机选择一个节点得到的大集团规模母函数的重整化形式为:
本身 [10] 。类似的,随机选择一个节点得到的大集团规模母函数的重整化形式为:
 (2.7)
(2.7)
在文献 [11] 中,Newman等人得到了传播速率的临界值 ,并给出它的表达式:
,并给出它的表达式:
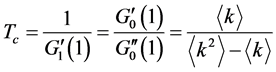 (2.8)
(2.8)
称 为流行病的阈值 [10] 。
为流行病的阈值 [10] 。
当 时,一场流行病或者用逾渗理论里的“大集团”就会出现,此时用
时,一场流行病或者用逾渗理论里的“大集团”就会出现,此时用 来表示大集团里感染的人数占总人数的比例,并且它等于:
来表示大集团里感染的人数占总人数的比例,并且它等于:
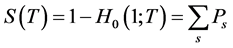 (2.9)
(2.9)
此时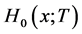 的意义发生变化,它不再是所有的簇的规模分布的母函数,而是除了大集团以外所有小规模的簇的母函数。利用方程(2.7)我们又可以得到流行病规模
的意义发生变化,它不再是所有的簇的规模分布的母函数,而是除了大集团以外所有小规模的簇的母函数。利用方程(2.7)我们又可以得到流行病规模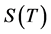 的另一个表达式:
的另一个表达式:
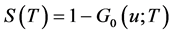 (2.10)
(2.10)
其中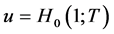 是自组织方程(2.6)的解,即:
是自组织方程(2.6)的解,即:
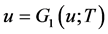 (2.11)
(2.11)
上面所提到的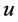 表示的是随机选择一条边,并沿着它到达的某个节点仍然是健康的易感节点的概率,且它的范围是在0到1之间。
表示的是随机选择一条边,并沿着它到达的某个节点仍然是健康的易感节点的概率,且它的范围是在0到1之间。
基于上述结论,我们可以研究关于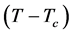 的爆发流行的标度律
的爆发流行的标度律 ,即:
,即:
 (2.12)
(2.12)
其中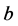 表示不同结构下的传染病爆发流行的标度律系数。
表示不同结构下的传染病爆发流行的标度律系数。
3. 标度律
把式(2.4)和式(2.11)结合起来得到:
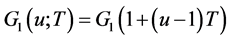 (3.1)
(3.1)
这时令 ,而
,而 ,
,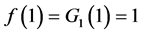 ;它的导数
;它的导数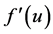 、
、 都是恒大于0的,也就是说,函数
都是恒大于0的,也就是说,函数 在区间
在区间 上是单调递增且是凸的。并且
上是单调递增且是凸的。并且
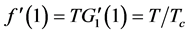 (3.2)
(3.2)
而式(2.11)可以变形为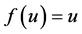 。当
。当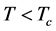 (
(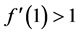 )时,该方程只有唯一的正解
)时,该方程只有唯一的正解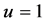 ;而当
;而当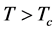 (
( )时,方程除了1以外还有一个
)时,方程除了1以外还有一个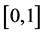 之间的解
之间的解 。从图1也可以直观地看出函数
。从图1也可以直观地看出函数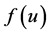 的性质以及解
的性质以及解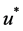 的存在。
的存在。
既然方程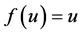 的存在性已经得到了证明了,那么很自然地下一步就想解出该方程并得到解的具体形式。接下来将考虑在阈值附近的解的具体形式。
的存在性已经得到了证明了,那么很自然地下一步就想解出该方程并得到解的具体形式。接下来将考虑在阈值附近的解的具体形式。
度分布的异质性将会导致不同的疾病传播模式。为了研究传染病的爆发流行对于传染速率的敏感度,我们必须得到自组织方程(2.11)的解。事实上,当 (
(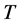 在
在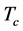 的附近)时,利用泰勒展开式,可以得到几种具体度分布下的方程的解
的附近)时,利用泰勒展开式,可以得到几种具体度分布下的方程的解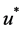 的具体形式。下面以泊松分布为例给出该情形下的具体推导过程。
的具体形式。下面以泊松分布为例给出该情形下的具体推导过程。
当节点的度分布 为泊松分布时,
为泊松分布时,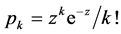 ,相应的母函数
,相应的母函数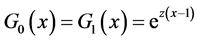 以及传播阈值
以及传播阈值 。此时方程(2.11)就变形为:
。此时方程(2.11)就变形为:
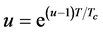 (3.3)
(3.3)
显然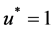 是方程(3.3)的一个根,另外利用泰勒展式得到单位根以外的解:
是方程(3.3)的一个根,另外利用泰勒展式得到单位根以外的解:
 (3.4)
(3.4)
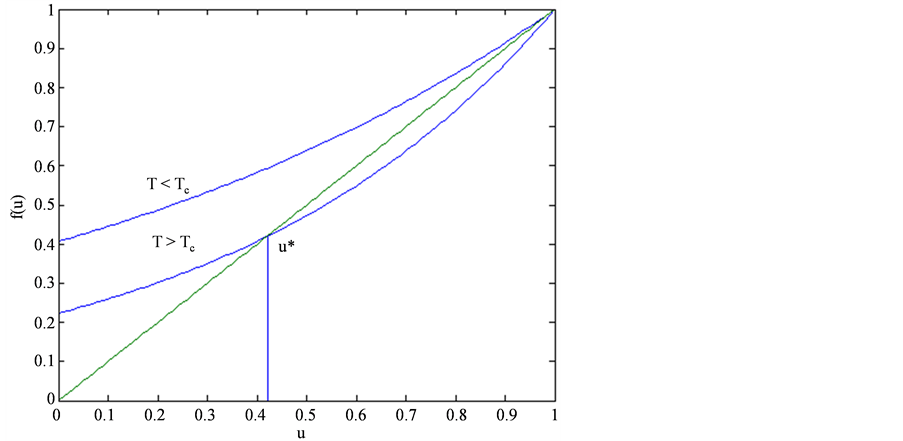
Figure 1. Two curves of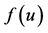 . When
. When , there exists unique intersection in
, there exists unique intersection in 
图1. 两种情形下的非平凡解的存在唯一性
其中 ,并且当
,并且当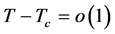 时,
时,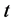 是一个无穷小量。此时方程(2.12)的左边
是一个无穷小量。此时方程(2.12)的左边
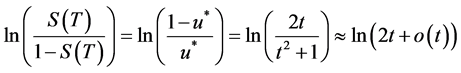 (3.5)
(3.5)
容易得到泊松分布的标度律系数近似为1。同质情形、两种节点和几何分布 [13] 标度律系数如表1所示(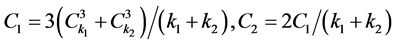 )。
)。
我们得到以上几种情形下的标度律系数都是1。
这里再考虑无标度网络的情形,即网络的底层结构服从幂律分布: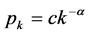 (
(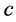 是归一化常数),文献 [14] 中对此情形作了分析计算。此时:
是归一化常数),文献 [14] 中对此情形作了分析计算。此时:
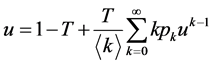 (3.6)
(3.6)
令 和
和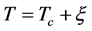 ,再利用近似:
,再利用近似:
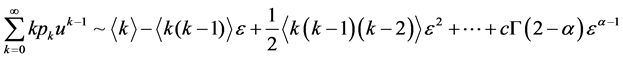 (3.7)
(3.7)
可以得到:
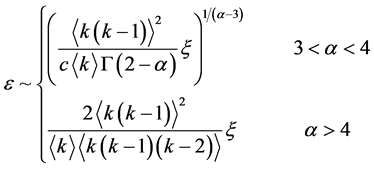 , (3.8)
, (3.8)
当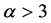 时,
时,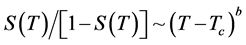 ,并得到标度律系数
,并得到标度律系数
Table 1. The values of the scaling law coefficient corresponding to different degree distributions
表1. 不同度分布下的标度律值
 , (3.9)
, (3.9)
但当 时,
时, ,得到当
,得到当 时标度律系数为
时标度律系数为 。
。
总之,当网络的度分布服从幂律分布时,此时SIR型传染病爆发流行的标度律系数是依赖于参数 的取值的,当
的取值的,当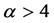 时,标度律系数和上述几种结构情形一样是为1的,此时也符合无穷维键逾渗的标度律情形。但当
时,标度律系数和上述几种结构情形一样是为1的,此时也符合无穷维键逾渗的标度律情形。但当 和
和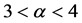 时,标度律系数是大于1的且等于
时,标度律系数是大于1的且等于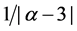 。
。
4. 结论
数学模型有助于我们更好地理解底层接触模式是如何影响传染病传播的,除此之外,理论分析的结果也有利于我们设计统计方案来收集和分析数据资料。与其它研究SIR传染病模型相比,本文的方法有下面两个优点:一是把随机图理论和无穷维的逾渗理论结合起来,这就使得对SIR型传染病模型的研究变得更简单;另一方面,用标度律来刻画对于传播速率爆发流行的影响,这就从宏观角度更好的说明了R. May所提到的现象 [1] 。
不同于Newman,我们给出了当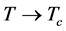 时,自组织方程(2.11)的解析解。利用那个不等于1的
时,自组织方程(2.11)的解析解。利用那个不等于1的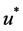 ,我们得到了包括同质、泊松分布和几何分布情形下SIR型传染病爆发流行的标度律系数,它们的值都是1。这个结果证实了逾渗理论中的结论,即:无穷维的逾渗模型的标度律都是一样的。另外我们发现当底层的网络结构是幂律分布时,此时爆发流行的标度律系数是与参数
,我们得到了包括同质、泊松分布和几何分布情形下SIR型传染病爆发流行的标度律系数,它们的值都是1。这个结果证实了逾渗理论中的结论,即:无穷维的逾渗模型的标度律都是一样的。另外我们发现当底层的网络结构是幂律分布时,此时爆发流行的标度律系数是与参数 相关的。
相关的。
基金项目
国家自然科学基金(11001004)。
文章引用
彭为花,王家赠. 异质群体中SIR型传染病爆发流行的标度律
A Scaling Law of the SIR Outbreak Prevalence in Heterogeneous Medias[J]. 应用数学进展, 2016, 05(04): 783-789. http://dx.doi.org/10.12677/AAM.2016.54090
参考文献 (References)
- 1. Meshal, R.A. (1991) Infectious Diseases of Humans. Oxford University Press, Location.
- 2. Woolhouse, M.E., Dye, C., Etard, J.F., et al. (1997) Heterogeneities in the Transmission of Infectious Agents: Implications for the Design of Control Programs. Proceedings of the National Academy of Sciences of the United States of America, 94, 338-342. https://doi.org/10.1073/pnas.94.1.338
- 3. CDC (2001) HIV Prevalence Trends in Selected Populations in the United States: Results from National Serosurveillance, 1993-1997. 1-51.
- 4. Lajmanovich, A. and Yorke, J.A. (1976) A Deterministic Model for Gonorrhea in a Nonhomogeneous Population. Mathematical Biosciences, 28, 221-236. https://doi.org/10.1016/0025-5564(76)90125-5
- 5. Hethcote, H.W. and Yorke, J.A. (1984) Gonorrhea Transmission Dynamics and Control. Springer-Verlag, Location. https://doi.org/10.1007/978-3-662-07544-9
- 6. Pastor-Satorras, R. and Vespignani, A. (2001) Epidemic Spreading in Scale-Free Networks. Physical Review Letters, 86, 3200-3203. https://doi.org/10.1103/PhysRevLett.86.3200
- 7. Boccaletti, S., Latora, V., Moreno, Y., Chavez, M.A. and Hwang, D.U. (2006) Complex Networks: Structure and Dynamics. Physics Reports, 424, 175-308. https://doi.org/10.1016/j.physrep.2005.10.009
- 8. Dorogovtsev, S.N., Goltsev, A.V. and Mendes, J.F.F. (2007) Critical Phenomena in Complex Networks. Review of Modern Physics, 80, 1275-1335. https://doi.org/10.1103/RevModPhys.80.1275
- 9. Sander, L.M., Warren, C.P., Sokolov, I.M., Simon, C. and Koopman, J. (2002) Percolation on Heterogeneous Networks as a Model for Epidemics. Mathematical Biosciences, 180, 293-305. https://doi.org/10.1016/S0025-5564(02)00117-7
- 10. Meyers, L. (2007) Contact Network Epidemiology: Bond Percolation Applied to Infectious Disease Prediction and Control. Bulletin of the American Mathematical Society, 44, 63-87.
- 11. Newman, M.E. (2002) Spread of Epidemic Disease on Networks. Physical Review E, 66, 016128. https://doi.org/10.1103/PhysRevE.66.016128
- 12. Durrett, R. (2006) Random Graph Dynamics (Cambridge Series in Statistical and Probabilistic Mathematics). Cambridge University Press. https://doi.org/10.1017/CBO9780511546594
- 13. Volz, E. (2008) Sir Dynamics in Random Networks with Heterogeneous Connectivity. Journal of Mathematical Biology, 56, 293-310. https://doi.org/10.1007/s00285-007-0116-4
- 14. Cohen, R., Benavraham, D. and Havlin, S. (2002) Percolation Critical Exponents in Scale-Free Networks. Physical Review E, 66, 1-20. https://doi.org/10.1103/physreve.66.036113
*通讯作者。
