Advances in Applied Mathematics
Vol.
10
No.
04
(
2021
), Article ID:
41810
,
14
pages
10.12677/AAM.2021.104113
非线性分数阶泛函微分方程组边值问题的 可解性
全欢
上海理工大学理学院,上海

收稿日期:2021年3月19日;录用日期:2021年4月6日;发布日期:2021年4月25日

摘要
本文研究了一类非线性分数阶泛函微分方程组边值问题正解的存在性。首先,将所研究的问题转化为积分方程形式,通过做变换得到等价积分方程。然后建立比较定理,运用上下解方法证明了边值问题正解的存在性。最后给出一个例子说明结论的适用性。
关键词
泛函微分方程,边值问题,Riemann-Liouville分数阶导数,上下解
Solvability for Boundary Value Problems of Nonlinear Fractional Functional Differential Systems
Huan Quan
College of Science, University of Shanghai for Science and Technology, Shanghai

Received: Mar. 19th, 2021; accepted: Apr. 6th, 2021; published: Apr. 25th, 2021

ABSTRACT
In this paper, the existence of positive solutions for a class of boundary value problems of nonlinear fractional functional differential system with time delays is studied. Firstly, the problems studied in this paper are transformed into integral equations, and the equivalent integral equation is obtained by transformation. Secondly, a comparison theorem is established and the existence of positive solutions of boundary value problem is proved by using upper and lower solution method. Finally, an example is given to illustrate the applicability of the conclusion.
Keywords:Functional Differential System, Boundary Value Problem, Riemann-Liouville Fractional Derivative, Upper and Lower Solutions

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,分数阶微分方程在化学工程、自动控制、热弹力学等领域得到广泛应用,分数阶微分方程的理论研究受到学者们的高度重视 [1] [2] [3] [4]。
在科学研究和工程技术领域等诸多领域中,如果假设事物的变化规律与过去的历史无关,只和当时的状态有关,那么可以用经典的微分方程刻画它的数学模型 [5] [6]。然而在实际需要中,许多事物的变化规律不仅依赖于当时的状态,还依赖于它过去和未来的发展状态。带时滞的泛函微分方程是刻画这类客观事物运动规律的数学模型。近年来,分数阶泛函微分方程边值问题受到研究者的关注,取得了很多研究成果 [7] [8] [9] [10]。
分数阶微分方程组在各大领域有着广泛应用,例如复数领域中的量子发展、动力系统、计算流体系统、生物遗传领域等 [11] - [21]。尽管分数阶微分方程组边值问题已经取得大量研究成果,但对分数阶泛函微分方程组的研究还不是很多。
基于前面提及的实际应用和研究成果,本文研究了一类非线性分数阶泛函微分方程组边值问题:
(1.1)
其中 , 。 , 是Riemann-Liouville分数阶导数, ,,,,,,且 ,。
2. 预备知识
首先,给出一些基本定义和引理。
定义2.1 [4] 函数 的 阶Riemann-Liouville分数积分定义为
,
等式的右端在 有定义。
定义2.2 [4] 连续函数 的 阶Riemann-Liouville分数阶导数定义为
,
只要等式的右端在 有定义。
引理2.1 [4] 假设n为正整数, ,则Riemann-Liouville分数阶微分方程 的通解为
,
其中 。
引理2.2 [4]
1) 若 , 则
, .
2) 若 , 则
.
引理2.3 设 ,。则边值问题
(2.1)
存在唯一解
, (2.2)
, (2.3)
其中
(2.4)
(2.5)
证明 假设 是边值问题(2.1)的解,由引理2.1可得,存在 使得
,
.
由边界条 可得, ,。所以
,
,
由引理2.2可得
,
,
因此,
,
,
由边界条件 , 可得
,
,
因此,边值问题(2.1)的唯一解是
.
类似地,
.
易证 满足(2.1),即为边值问题(2.1)的解。
证毕。
引理2.4 边值问题(1.1)等价于积分方程组
(2.6)
(2.7)
由 , 的表达式可以得到如下引理:
引理2.5 1) , 是 上的连续函数;
2) 对任意的 有
.
3) 对任意的 有
.
证明 1) 由函数 , 的表达式可知,函数 , 在 上连续;
2) 当 时,显然有 。当 时,有
,
因此,对任意的 ,都有 。
由(2.4)式可知,对任意的 ,都有
.
因此, 。
同理可证,对任意的 ,。
证毕。
令 ,定义范数 ,在 上定义范数 ,则 和 是Banach空间。
令
,
定义 上的范数 及 。显然, 且 是Banach空间, 是正规体锥。
对任意的 ,, 当且仅当 。于是 为半序的Banach空间。若 且 ,记为 ,若 ,记为 。
对函数 和 补充定义,当 时,令 。显然。 。
任意的 ,设
因此,对任意 , ,有
, .
易得到以下引理:
引理2.6 是方程组(2.6) (2.7)的解当且仅当 是积分方程组
(2.8)
(2.9)
的解。因此 是方程组(3.1)的解当且仅当 是泛函微分方程组
(2.10)
的解。
3. 解的存在性
定义3.1设 ,若 满足(1.1)中各等式,那么我们称 是边值问题(1.1)的一个解,若当 时, ,,则称 为边值问题(1.1)的一个正解。
定义3.2设 ,如果
(3.1)
则称 是边值问题(2.10)的上解。
定义3.3 设 ,如果
(3.2)
则称 是边值问题(2.10)的下解。
引理3.1 (比较定理)设 ,如果 满足
(3.3)
则当 时, ,。
证明 令 ,,,。由 , , , 及引理2.3,边值问题
有唯一解
由引理2.5,当 时, ,。
证毕。
为了证明方便,先给出如下假设:
(H) 任意的 和任意的 , 当 ,,对任意的 ,有
, , , .
引理3.2假如(H)成立,边值问题(1.1)存在上解 和下解 ,且 。若 满足
(3.4)
(3.5)
则 ,且 , 分别是边值问题(1.1)的上解和下解。
证明 由引理2.3可得 , 有定义。
由上解的定义及(3.4)可得,对任意 ,
,
,
,
.
对任意的 ,
, .
由引理3.1可得,当 时,
 ,
,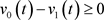 .
.
所以
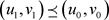 .
.
类似地,容易证明 。
。
由(3.4),(3.5)及(H)可得,对任意 ,
,
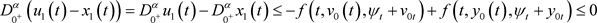 ,
,
 ,
,
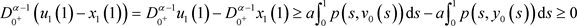 ,
,
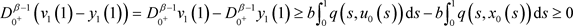 .
.
对于任意的 时,
时,
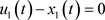 ,
,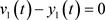 .
.
由引理3.1得,当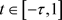 时,
时,
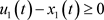 ,
,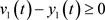 .
.
所以
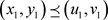 .
.
综上所述 。
。
对任意的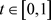 ,由(3.4)和(H)可得
,由(3.4)和(H)可得
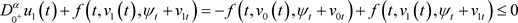 ,
,
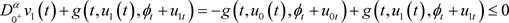 ,
,
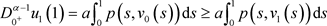 ,
,
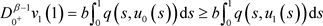 ,
,
所以
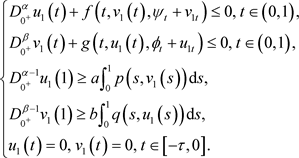
由上解定义可得 是边值问题(1.1)的上解。
是边值问题(1.1)的上解。
类似地,容易证明 是边值问题(1.1)的下解。
是边值问题(1.1)的下解。
证毕。
记序区间
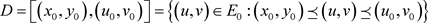 .
.
定理3.1 假设(H)成立,若存在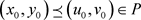 ,且
,且 和
和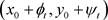 分别是边值问题(1.1)的上解和下解。则边值问题(1.1)存在两个正解
分别是边值问题(1.1)的上解和下解。则边值问题(1.1)存在两个正解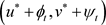 ,
,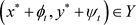 ,且
,且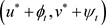 ,
,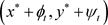 分别是边值问题(1.1)在该区间上的最大正解和最小正解。
分别是边值问题(1.1)在该区间上的最大正解和最小正解。
证明 分别以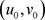 ,
,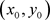 为初始元,通过迭代公式
为初始元,通过迭代公式
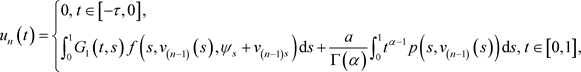 (3.6)
(3.6)
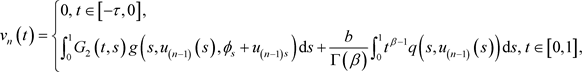 (3.7)
(3.7)
和
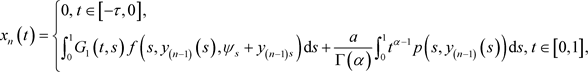 (3.8)
(3.8)
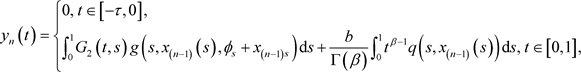 (3.9)
(3.9)
产生两个序列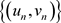 ,
,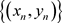 。由引理2.3知
。由引理2.3知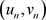 ,
, 分别为边值问题
分别为边值问题
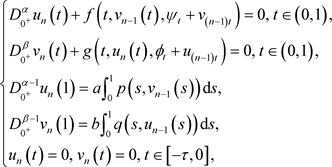 (3.10)
(3.10)
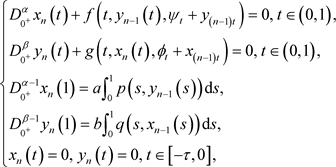 (3.11)
(3.11)
的唯一解。
由引理3.2可得
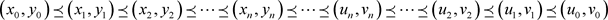 .
.
易知序列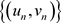 ,
,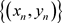 都一致有界,即存在常数
都一致有界,即存在常数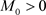 使得对任意的
使得对任意的 ,都有
,都有
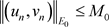 ,
, 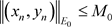 ,
,
因此
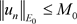 ,
,  ,
, 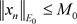 ,
, .
.
因为
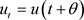 ,
, .
.
所以对任给定的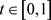 ,任意的
,任意的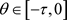 ,由
,由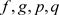 的连续性可知,存在常数
的连续性可知,存在常数 ,
,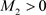 ,
,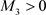 ,
,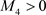 使得任意的
使得任意的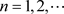 ,都有
,都有
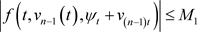 ,
, 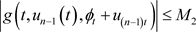 ,
,
 ,
, .
.
对任意的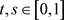 ,由于
,由于 ,
,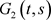 在
在 上连续,故
上连续,故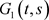 ,
,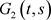 在
在 上一致连续。对任意的
上一致连续。对任意的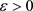 ,存在
,存在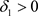 ,当
,当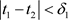 时,有
时,有
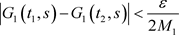 ,
,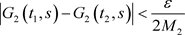 .
.
因为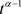 ,
, 在
在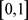 上连续,所以
上连续,所以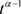 ,
,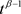 在
在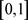 上一致连续。对于上述
上一致连续。对于上述 ,存在
,存在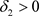 ,当
,当 时,有
时,有
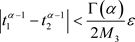 ,
, .
.
取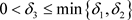 ,则
,则
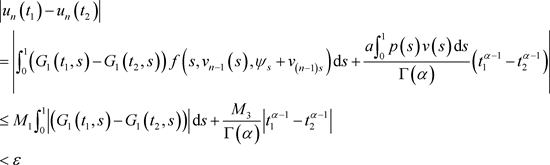 .
.
类似地,可以证明任意的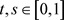 时,对任意的
时,对任意的 ,存在
,存在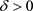 ,当
,当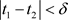 时,有
时,有
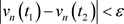 .
.
所以函数列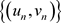 等度连续,由Ascoli-Arzela定理可知函数列
等度连续,由Ascoli-Arzela定理可知函数列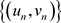 相对列紧。类似地,容易证明
相对列紧。类似地,容易证明 相对列紧。又因为
相对列紧。又因为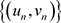 ,
, 是单调的,所以存在
是单调的,所以存在 ,
,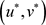 使得
使得
 ,
,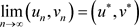 .
.
这就暗示 是边值问题(2.10)的一个下解,
是边值问题(2.10)的一个下解,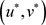 是边值问题(2.10)的一个上解,且
是边值问题(2.10)的一个上解,且 。
。
由(3.6),(3.7)及Lebegsgue控制收敛定理,有
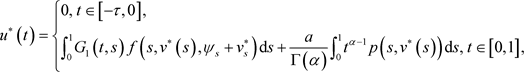

由引理2.3可知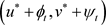 是边值问题(1.1)的解。类似地,容易证明
是边值问题(1.1)的解。类似地,容易证明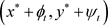 是边值问题(1.1)的解。
是边值问题(1.1)的解。
假设 是边值问题(2.10)在Y中的解,则
是边值问题(2.10)在Y中的解,则 。 假设对任意正整数n,
。 假设对任意正整数n,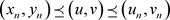 都成立。与引理3.2类似可证
都成立。与引理3.2类似可证
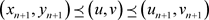 .
.
由数学归纳法可得,对任意的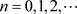 ,有
,有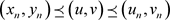 。
。
由迭代序列的收敛性可得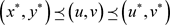 。所以
。所以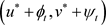 ,
,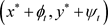 分别是边值问题(1.1)在Y上的最大正解和最小正解。
分别是边值问题(1.1)在Y上的最大正解和最小正解。
证毕。
4. 例子
为了说明结论的适用性,我们考虑如下非线性分数阶泛函微分方程组边值问题:
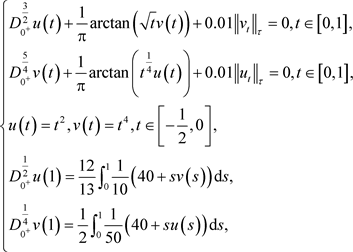 (4.1)
(4.1)
其中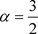 ,
,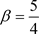 ,
,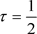 ,
, ,
,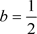 ,
, ,
, ,
, ,
, ,
,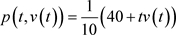 ,
,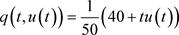 。
。
对任意的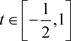 ,取
,取
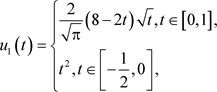
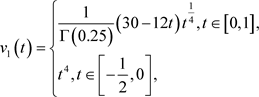
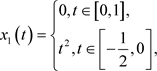
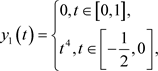
由于
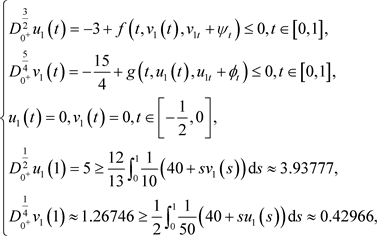
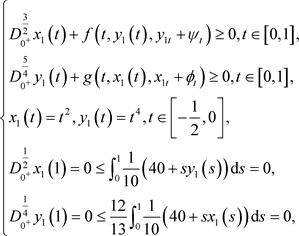
则 ,
,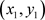 分别为边值问题(4.1)的上解和下解,且满足
分别为边值问题(4.1)的上解和下解,且满足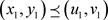 。
。
另一方面,对任意的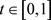 ,
,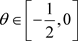 ,
,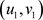 ,
,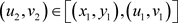 ,当
,当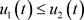 ,
,
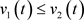 时
时
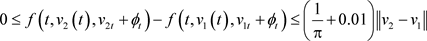 ,
,
 ,
,
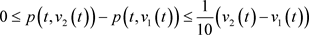 ,
,
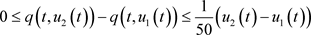 ,
,
满足条件(H)。由定理3.1可得,边值问题(17)在Y中的正解为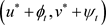 ,
, ,且
,且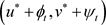 ,
, 分别是边值问题(4.1)的最大正解和最小正解。
分别是边值问题(4.1)的最大正解和最小正解。
文章引用
全 欢. 非线性分数阶泛函微分方程组边值问题的可解性
Solvability for Boundary Value Problems of Nonlinear Fractional Functional Differential Systems[J]. 应用数学进展, 2021, 10(04): 1039-1052. https://doi.org/10.12677/AAM.2021.104113
参考文献
- 1. 白占兵. 分数阶微分方程边值问题理论及应用[M]. 北京: 中国科学技术出版社, 2013: 2-4.
- 2. 郭大均, 孙经先, 刘兆理. 非线性常微分方程泛函方法[M]. 济南: 山东科学技术出版社, 2005: 219-222.
- 3. Podlubny, I. (1999) Fractional Differential Equations. Academic Press, San Diego.
- 4. Kilbas, A.A., Srivastava, H.M. and Trujillo, J.J. (2006) Theory and Applications of Fractional Differential Equations. Elsevier B.V., Amsterdam, 69-79.
- 5. 郑祖庥. 泛函微分方程理论[M]. 合肥: 安徽教育出版社, 1994.
- 6. 郑祖庥. 泛函微分方程的发展和应用[J]. 数学进展, 1983, 12(2): 94-112.
- 7. 彭世国, 朱思铭. 泛函微分方程周期边值问题的正解[J]. 数学年刊, 2005, 26(3): 419-426.
- 8. Su, X. (2012) Positive Solutions to Singular Boundary Value Problems for Fractional Functional Differential Equations with Changing Sign Nonlinearity. Computers and Mathematics with Applications, 64, 3425-3435. https://doi.org/10.1016/j.camwa.2012.02.043
- 9. Zhao, K. and Wang, K. (2016) Existence of Solutions for the Delayed Nonlinear Fractional Functional Differential Equations with Three-Point Integral Boundary Value Conditions. Advances in Difference Equations, 2016, Article No. 284. https://doi.org/10.1186/s13662-016-1012-2
- 10. Zhu, B., Liu, L. and Wu, Y. (2019) Existence and Uniqueness of Global Mild Solutions for a Class of Nonlinear Fractional Reaction-Diffusion Equations with Delay. Computers and Mathematics with Application, 78, 1811-1818. https://doi.org/10.1016/j.camwa.2016.01.028
- 11. Du, X., Meng, Y. and Pang, H. (2020) Iterative Positive Solutions to a Coupled Hadamard-Type Fractional Differential System on Infinite Domain with the Multistrip and Multipoint Mixed Boundary Conditions. Journal of Functional Analysis, 2020, Article ID: 6508075. https://doi.org/10.1155/2020/6508075
- 12. Liu, X. and Jia, M. (2019) Solvability and Numerical Simulations for BVPs of Fractional Coupled Systems Involving Left and Right Fractional Derivatives. Applied Mathematics and Computers, 353, 230-242. https://doi.org/10.1016/j.amc.2019.02.011
- 13. Zeeshan, A., Akbar, Z. and Kamal, S. (2019) On Ulam’s Stability for a Coupled Systems of Nonlinear Implicit Fractional Differential Equations. Bulletin of the Malaysian Mathematical Science, 42, 2681-2699. https://doi.org/10.1007/s40840-018-0625-x
- 14. Asif, N.A. and Khao, R.A. (2012) Positive Solutions to Singular System with Four-Point Coupled Boundary Conditions. Journal of Mathematical Analysis and Application, 386, 848-861. https://doi.org/10.1016/j.jmaa.2011.08.039
- 15. Zhang, Y., Bai, Z. and Feng, T. (2011) Existence Results for a Coupled System of Nonlinear Fractional Three-Point Boundary Value Problems at Resonance. Computers and Mathematics with Application, 61, 1032-1047. https://doi.org/10.1016/j.camwa.2010.12.053
- 16. Hou, Y., Zhang, L. and Wang, G. (2018) A New Comparison Principle and Its Application to Nonlinear Impulsive Functional Integro-Differential Equations. Advances in Difference Equations, 2018, Article No. 380. https://doi.org/10.1186/s13662-018-1849-7
- 17. Faieghi, M., Kuntanapreeda, S. and Beleanu, D. (2013) LMI-Based Stabilization of a Class of Fractional-Order Chaotic Systems. Nonlinear Dynamics and Systems Theory, 72, 301-309. https://doi.org/10.1007/s11071-012-0714-6
- 18. Ionkin, N.I. (1977) Solution of a Boundary-Value Problem in Heat Conduction with a Non-Classical Boundary Condition. Differential Equations, 13, 294-304.
- 19. Ahmad, B., Ntouyas, S. and Alsaedi, A. (2014) Existence Results for a System of Coupled Hybrid Fractional Differential Equations. Abstract and Applied Analysis, 2014, Article ID: 672167. https://doi.org/10.1155/2014/426438
- 20. Zhang, F. (2013) The Synchronization of a Fractional-Order Chaotic System. Advanced Materials Research, 655, 1488-1491. https://doi.org/10.4028/www.scientific.net/AMR.655-657.1488
- 21. Zhang, X., Liu, L. and Wu, Y. (2013) The Uniqueness of Positive Solution for a Singular Fractional Differential System Involving Derivatives. Communications in Nonlinear Science and Numerical Simulation, 18, 913-919. https://doi.org/10.1016/j.cnsns.2012.08.033