Toric曲面的渐进迭代逼近 Progressive Iterative Approximation of Toric Surfaces

doi:10.12677/AAM.2023.1212507

Advances in Applied Mathematics
Vol. 12 No. 12 ( 2023 ), Article ID: 77990 , 9 pages
10.12677/AAM.2023.1212507

Toric曲面的渐进迭代逼近

段卓，彭兴璇^*

●How to Cite this Article

辽宁师范大学数学学院，辽宁大连

收稿日期：2023年11月25日；录用日期：2023年12月19日；发布日期：2023年12月26日

摘要

渐进迭代逼近(PIA)是一种直观有效的数据拟合方法。当给定数据点的参数域为不规则的凸多边形时，需要对参数域剖分来用多片曲面拟合，然后考虑相邻曲面片的拼接。Toric曲面是Bézier曲面的推广，它的参数域可以调整为任意凸多边形。使用Toric曲面做渐进迭代逼近即可以保留渐进迭代逼近的优点，也可以整体对数据点进行拟合，无需考虑曲面的重构与拼接。本篇文章定义了一种对凸多边形上的参数点进行字典排序的方法。并实现了一种用Toric曲面做渐进迭代逼近的算法。我们还用具体的数值例子证明方法有效。

关键词

Toric曲面，渐进迭代逼近(PIA)，数据拟合，Bézier曲面

Progressive Iterative Approximation of Toric Surfaces

Zhuo Duan, Xingxuan Peng^*

School of Mathematics, Liaoning Normal University, Dalian Liaoning

Received: Nov. 25^th, 2023; accepted: Dec. 19^th, 2023; published: Dec. 26^th, 2023

ABSTRACT

Progressive iterative approximation (PIA) is an intuitive and effective data fitting method. When the parameter domain of a given data point is an irregular convex polygon, the parameter domain needs to be partitioned to be fitted by a multi-piece surface. Then we consider the stitching of adjacent surface patches. Toric surfaces are a generalization of Bézier surfaces whose parametric domain can be adjusted to any convex polygon. Using Toric surface for progressive iterative approximation can not only retain the advantages of progressive iterative approximation, but also fit the data points as a whole, without considering the reconstruction and splicing of the surface. This paper defines a lexicographic method for sorting the points of a convex polygon. A progressive iterative approximation algorithm using Toric surfaces is also implemented. We also use specific numerical examples to prove that the method is effective.

Keywords:Toric Surface, Progressive Iterative Approximation (PIA), Data Fitting, Bézier Surface

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

数据拟合是处理科学和工程问题中大量采样和实验数据的常用方法。它通过将离散的数据拟合为连续的代数表示来反映数据的基本趋势。渐进迭代逼近(Progressive Iterative Approximation, PIA)是一种有效的数据拟合方法，它使用几何迭代法动态求解，具有明显的几何意义。渐进迭代逼近方法被广泛应用于几何设计、数据拟合、网格和样条体的生成、逆向工程以及图像处理等领域。它的优点包括直观操作、简单算法和强适应性。

曲线曲面渐进迭代逼近性质的研究自上世纪70年代开始。齐东旭等 [1] 提出了均匀三次B样条曲线盈亏修正算法，并发现这种曲线具有PIA性质。Lin等 [2] 证明非均的三次B样条曲线曲面也具有PIA特性。2005年，Lin等 [3] 证明了在非退化配置矩阵的情况下，曲线(包括张量积曲面)具有渐进迭代逼近性质。张莉 [4] 将PIA的适用范围推广到三角域上，给出了三角片面Bézier曲面具有PIA性质的条件。胡倩倩 [5] 等人对PIA算法进行了改进实现了三角B-B曲面加速逼近的算法，使算法更加高效。Liu [6] 等人研究了张量积Bézier曲面的PIA性质。近年来PIA算法在各种曲线曲面逼近上得到了广泛的应用。季康松 [7] 等给PIA加入了法相约束，使隐式曲线能够更好地拟合散乱数据点及其几何特征。吴硕琳 [8] 等在PIA算法的基础上提出了非均匀三次B样条曲线Hermite插值算法，并证明了该算法是收敛的。周晨 [9] 等实现了用非均匀3次B样条拟合曲线的PIA性质实现了一种矢量地图曲线化简方法，展现出PIA算法在实际生活中有广泛的应用。

Toric曲面是张量积Bézier曲面和三角Bézier曲面片的推广，具有许多与Bézier曲面相类似的良好性质。2002年Ktasauskas [10] 基于Toric簇和Torie理想，定义了一类与整数点集下的有理多边形参数曲面Toric曲面。Toric曲面与Bézier曲面相比，在曲面拼接 [11] 、曲面补洞 [12] 、过渡曲面 [13] 等应用中，Toric方法需要更少的曲面片，整体性更好。汪涵 [14] 等在Toric-Bézier曲线上加入了伸缩因子实现曲线的自由变形，提高了曲线的可调性和预见性。孙兰银等 [15] 利用最小二乘法实现了Toric曲面拟合数据点。2020年，Li [16] 等定义了一种特殊的Toric曲线并将其命名为GT-Bézier曲线，这种曲线是Bézier曲线的拓展。Yu [17] 发现了一种特殊的Toric曲线，并证明了这种曲线具有PIA性。

本文在现有渐进迭代逼近方法的研究基础上，研究Toric曲面的渐进迭代逼近算法。得出当普半径小于1时，Toric曲面同样可以渐进迭代逼近数据点。定义了一种字典排序的方法，将选取的参数点按字典排序，将Toric曲面做渐进迭代逼近使其逐渐靠近这些数据点，最终得到了拟合这些数据点的Toric曲面。本文的第一章介绍了Toric曲面的定义和字典排序方法为下文做准备。第二章讲解了Toric曲面做渐进迭代逼近的过程。第三章给出了数值实例可以直观地看出拟合效果。相较于别的曲面渐进迭代逼近，Toric曲面的参数域选取更加灵活，可以是任意凸多边形。对于不规则形状的参数域，可以直接用Toric曲面做整体拟合，无需考虑曲面的重构与拼接。

2. 预备知识

定义1. (Toric-Bernstein基函数)：设在平面中，坐标为整数的有限个点构成的集合为 $A \subset ℤ^{2}$ 。设该点集A的凸包 $c o n v (A)$ 为 $Δ A$ 。令n边形 $Δ A$ 的第r条边的边界方程为 $l_{r} (u, v) : a_{r} u + b_{r} v + c_{r} = 0$ ， $r = 1, 2, \dots, n$ 。这里的 $a_{r}, b_{r}, c_{r}$ 互素且向量 $〈 a_{r}, b_{r} 〉$ 指向 $Δ A$ 的内部。那么对于集合A中的每一个整数格点 $(i, j) \in A$ ，定义Toric-Bernstein基函数为：

$B_{i, j} (u, v) = C_{i, j} l_{1} {(u, v)}^{l_{1} (i, j)} l_{2} {(u, v)}^{l_{2} (i, j)} \dots l_{n} {(u, v)}^{l_{n} (i, j)} (u, v) \in Δ A$ (1)

其中 $C_{i, j} > 0$ 为自定义系数。

定义2. (Toric曲面)：对于有限整数点集A，定义在 $Δ A$ 上的Toric Bézier曲面为 $F_{A, ω, B} (u, v)$ 为：

$F_{A, ω, B} (u, v) = \frac{\sum_{(i, j) \in A} ω_{i, j} p_{i, j} B_{i, j} (u, v)}{\sum_{(i, j) \in A} ω_{i, j} B_{i, j} (u, v)} (u, v) \in Δ A$ (2)

其中 $B_{i, j} (u, v)$ 是Toric-Bernstein基函数， $p_{i, j} \in ℝ^{3}$ 为对应整数格点 $(i, j) \in A$ 的控制顶点， $ω_{i, j}$ 为控制顶点的权因子。

因为Toric曲面定义在 $Δ A$ 上， $Δ A$ 可能是一个不规则图形。为了描述方便需要给这些整数点集进行排序，下面给出字典排序的定义：

定义3. (字典排序)：设平面 $ℤ^{2}$ 中有两个坐标为整数的点 $(i, j)$ 和 $(i^{'}, j^{'})$ ，若 $(i, j) > (i^{'}, j^{'})$ 成立，当且仅当 $i > i^{'}$ 或( $i = i^{'}$ 且 $j > j^{'}$ )。

设点集A有n个坐标为整数的点，可以用字典排序的方法从小到大将点集A重新排列为 $A = {a_{1}, a_{2}, \dots, a_{n}}$ 。那么Toric-Bernstein基函数可以写成，

$B_{a_{k}} (u, v) = C_{a_{k}} l_{1} {(u, v)}^{l_{1} (a_{k})} l_{2} {(u, v)}^{l_{2} (a_{k})} \dots l_{n} {(u, v)}^{l_{n} (a_{k})} (u, v) \in Δ A, k = 1, 2, \dots, n$

其中 $C_{a_{k}}$ 为自定义系数。同理，Toric曲面可以写成，

$F_{A, ω, B} (u, v) = \frac{\sum_{k = 1}^{n} ω_{a_{k}} p_{a_{k}} B_{a_{k}} (u, v)}{\sum_{k = 1}^{n} ω_{a_{k}} B_{a_{k}} (u, v)} (u, v) \in Δ A$

3. Toric曲面渐进迭代逼近

已知空间 $ℝ^{3}$ 中有n个数据点的集合 ${p_{i, j} | (i, j) \in A}$ ，每一个数据点 $p_{i, j}$ 对应的参数值为 $(i, j)$ ，它们组成平面有限点集A。将点集A中的点进行从小到大的字典排序可以将A写成点列 $A = {a_{1}, a_{2}, \dots, a_{n}}$ ，这样集合 ${p_{i, j} | (i, j) \in A}$ 可以按照角标的字典排序变为 ${p_{a_{k}}}_{k = 1}^{n}$ 。同样的也对点集A中的每一顶点的参数值进行字典排序，设排序后的参数值为集合 ${t_{a_{k}}}_{k = 1}^{n}$ 。通过点集A可以得到凸包 $Δ A$ ，并得到 $Δ A$ 对应的边界方程以及A中任意一点对应的Toric-Bernstein 基函数。通过预先自定义好的Toric-Bernstein基系数 $C_{a_{k}}$ ，以及每个参数点对应的权因子 $ω_{a_{k}}$ 。设定迭代的初始控制顶点为 ${p_{a_{k}}^{0} = p_{a_{k}}}_{k = 1}^{n}$ 。这样我们可以得出初始迭代Toric曲面：

$F_{A, ω, B}^{0} (u, v) = \frac{\sum_{k = 1}^{n} ω_{a_{k}} p_{a_{k}}^{0} B_{a_{k}} (u, v)}{\sum_{k = 1}^{n} ω_{a_{k}} B_{a_{k}} (u, v)} (u, v) \in Δ A$

之后计算每个控制顶点需要调整的向量 ${δ_{i}}_{i = 0}^{n}$

$δ_{a_{k}}^{0} = p_{a_{k}} - F_{A, ω, B}^{0} (t_{a_{k}}) k = 1, 2, \dots, n$

我们可以得到第二次迭代Toric曲面的控制顶点

$p_{a_{k}}^{1} = p_{a_{k}}^{0} + δ_{a_{k}}^{0} k = 1, 2, \dots, n$

最终得到新的曲面 $F_{A, ω, B}^{1} (u, v)$

$F_{A, ω, B}^{1} (u, v) = \frac{\sum_{k = 1}^{n} ω_{a_{k}} p_{a_{k}}^{1} B_{a_{k}} (u, v)}{\sum_{k = 1}^{n} ω_{a_{k}} B_{a_{k}} (u, v)} (i, j) \in A$

同理，我们可以通过曲面 $F_{A, ω, B}^{m} (u, v)$ 得到曲面 $F_{A, ω, B}^{i + 1} (u, v)$

$δ_{a_{k}}^{m} = p_{a_{k}} - F_{A, ω, B}^{m} (t_{a_{k}}) k = 1, 2, \dots, n$

$p_{a_{k}}^{m + 1} = p_{a_{k}}^{m} + δ_{a_{k}}^{m} k = 1, 2, \dots, n$

$F_{A, ω, B}^{m + 1} (u, v) = \frac{\sum_{k = 1}^{n} ω_{a_{k}} p_{a_{k}}^{k + 1} B_{a_{k}} (u, v)}{\sum_{k = 1}^{n} ω_{a_{k}} B_{a_{k}} (u, v)} (u, v) \in Δ A$

如果 $\lim_{m \to \infty} F_{A, ω, B}^{m} (a_{k}) = p_{a_{k}}, k = 1, 2, \dots, n$ 成立。我们可以称初始曲面 $F_{A, ω, B}^{m} (a_{k})$ 有PIA性。下面我们分析一下渐进迭代逼近收敛的条件。

$δ_{a_{k}}^{m + 1} = δ_{a_{k}}^{m} - \sum_{i = 1}^{n} δ_{a_{i}}^{m} \frac{ω_{a_{i}} B_{a_{i}} (t_{a_{k}})}{\sum_{j = 1}^{n} ω_{a_{j}} B_{a_{j}} (t_{a_{k}})} k = 1, 2, \dots, n; m = 0, 1, \dots$

上式写成矩阵的形式为

${[δ_{a_{1}}^{m + 1}, δ_{a_{2}}^{m + 1}, \dots, δ_{a_{n}}^{m + 1}]}^{T} = (I - B) {[δ_{a_{1}}^{m}, δ_{a_{2}}^{m}, \dots, δ_{a_{n}}^{m}]}^{T} m = 0, 1, \dots$

这里的I是指 $(n + 1) \times (n + 1)$ 的单位矩阵，矩阵B定义为

$B : = [\begin{matrix} \frac{ω_{a_{1}} B_{a_{1}} (t_{a_{1}})}{\sum_{j = 1}^{n} ω_{a_{j}} B_{a_{j}} (t_{a_{1}})} & \frac{ω_{a_{2}} B_{a_{2}} (t_{a_{1}})}{\sum_{j = 1}^{n} ω_{a_{j}} B_{a_{j}} (t_{a_{1}})} & \dots & \frac{ω_{a_{n}} B_{a_{n}} (t_{a_{1}})}{\sum_{j = 1}^{n} ω_{a_{j}} B_{a_{j}} (t_{a_{1}})} \\ \frac{ω_{a_{1}} B_{a_{1}} (t_{a_{2}})}{\sum_{j = 1}^{n} ω_{a_{j}} B_{a_{j}} (t_{a_{2}})} & \frac{ω_{a_{2}} B_{a_{2}} (t_{a_{2}})}{\sum_{j = 1}^{n} ω_{a_{j}} B_{a_{j}} (t_{a_{2}})} & \dots & \frac{ω_{a_{n}} B_{a_{n}} (t_{a_{2}})}{\sum_{j = 1}^{n} ω_{a_{j}} B_{a_{j}} (t_{a_{2}})} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ \frac{ω_{a_{1}} B_{a_{1}} (t_{a_{n}})}{\sum_{j = 1}^{n} ω_{a_{j}} B_{a_{j}} (t_{a_{n}})} & \frac{ω_{a_{2}} B_{a_{2}} (t_{a_{n}})}{\sum_{j = 1}^{n} ω_{a_{j}} B_{a_{j}} (t_{a_{n}})} & \dots & \frac{ω_{a_{n}} B_{a_{n}} (t_{a_{n}})}{\sum_{j = 1}^{n} ω_{a_{j}} B_{a_{j}} (t_{a_{n}})} \end{matrix}]$ (3)

当矩阵 $(I - B)$ 的普半径 $ρ (I - B) < 1$ 时渐进迭代收敛，当我们要使用Toric Bézier曲面做渐进迭代逼近时，需要提前计算出 $ρ (I - B)$ 以确保收敛。

Toric曲面的渐进迭代逼近算法：

输入：空间 $ℝ^{3}$ 中的n个数据点 ${p_{a_{k}}}_{k = 1}^{n}$ ，每个数据点对应的权因子 ${ω_{a_{k}}}_{k = 1}^{n}$ 和迭代次数 $\hat{m}$ 。

输出：对数据点 ${p_{a_{k}}}_{k = 1}^{n}$ 的m次渐进迭代逼近后的Toric Bézier曲面。

Step 1：根据数据点集 ${p_{a_{k}}}_{k = 1}^{n}$ 的确定点集A以及 $Δ A$ ，并由此得出Toric-Bernstein基函数 ${B_{a_{k}} (u, v)}_{k = 1}^{n}$ ，代入到矩阵(3)中求出普半径 $ρ (I - B)$

Step 2：当普半径 $ρ (I - B) < 1$ 时：

Step 2.1：令迭代次数 $m = 0$ 并计算初始Toric Bézier曲面控制顶点 ${p_{a_{k}}^{0} = p_{a_{k}}}_{k = 1}^{n}$

Step 2.2：计算误差 $δ_{a_{k}}^{m} = p_{a_{k}} - F_{A, ω, B}^{m} (a_{k})$ ，和新的控制顶点 $p_{a_{k}}^{m + 1} = p_{a_{k}}^{m} + δ_{a_{k}}^{m}$

Step 2.3：若 $m < \hat{m}$ ，令 $m = m + 1$ 回到第Step 2.2；若 $m = \hat{m}$ ，输出Toric Bézier曲面

$F_{A, ω, B}^{m + 1} (u, v) = \frac{\sum_{k = 1}^{n} ω_{a_{k}} p_{a_{k}}^{k + 1} B_{a_{k}} (u, v)}{\sum_{k = 1}^{n} ω_{a_{k}} B_{a_{k}} (u, v)} (u, v) \in Δ A$

Step 3：当普半径 $ρ (I - B) \geq 1$ 时：重新调整权因子 ${ω_{a_{k}}}_{k = 1}^{n}$ 或取样点 ${p_{a_{k}}}_{k = 1}^{n}$

4. 数值实例

例1：设空间 $ℝ^{3}$ 中有8个数据点按词典顺序为 $p_{0, 0} = (0, 0, 1)$ ， $p_{0, 1} = (0, 1, 2)$ ， $p_{0, 2} = (0, 2, 1)$ ， $p_{1, 0} = (1, 0, 2)$ ， $p_{1, 1} = (1, 1, 3)$ ， $p_{1, 2} = (1, 2, 1)$ ， $p_{2, 0} = (2, 0, 1)$ ， $p_{2, 1} = (2, 1, 1)$ ，视每一点的权因子都为1。可得 $A = {a_{1}, a_{2}, \dots, a_{8}} = {(0, 0), (0, 1), \dots, (2, 1)}$ 。 $Δ A$ 如图1所示。计算出toric-Bernstein基函数 ${B_{a_{k}} (u, v)}_{k = 1}^{n}$ ，并求出普半径 $ρ (I - B) = 0.875$ 证明在此基函数下Toric Bézier曲面渐进迭代逼近收敛。逼近效果如图2~4所示：

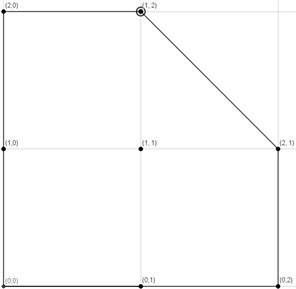
Figure 1. $A$ and $Δ A$

图1. $A$ 和 $Δ A$

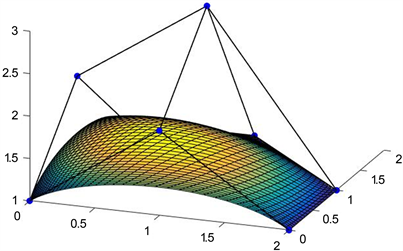
Figure 2. The initial Toric surface

图2. 初始Toric曲面

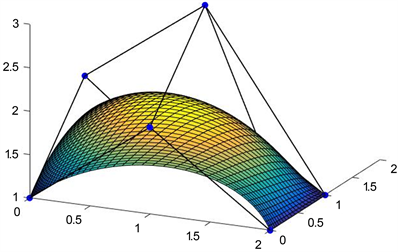
Figure 3. The surface after 1 iteration

图3. 迭代1次后的曲面

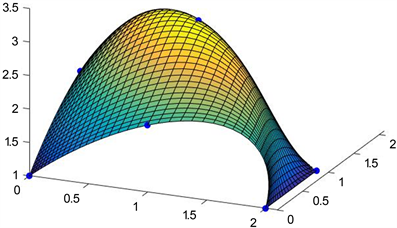
Figure 4. The surface after 50 iteration

图4. 迭代50次后的曲面

例2：如图5所示的凸图形 $A = {a_{1}, a_{2}, \dots, a_{19}} = {(0, 0), (0, 1), \dots, (4, 4)}$ 中取19个数据采集点，并在函数上 $f (u, v) = u^{2} + v^{2}$ 上找到每个数据采集点对应的数值大小如图6，并将他们按照字典排序，不失一般性可设每个拟合点对应的权因子都为1。求出普半径 $ρ (I - B) = 0.966$ 证明迭代是收敛的。迭代次数与渐进逼近效果如图7所示。

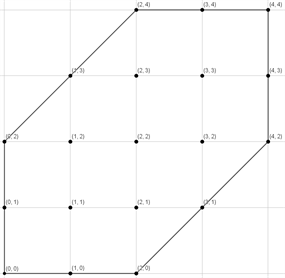
Figure 5. $A$ and $Δ A$

图5. $A$ 和 $Δ A$

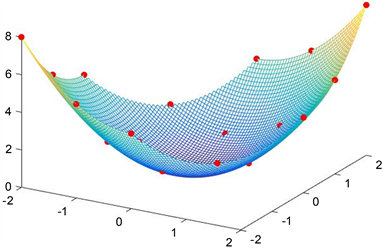
Figure 6. $f (u, v)$ and data point ${p_{a_{k}}}_{k = 1}^{n}$

图6. $f (u, v)$ 和数据点 ${p_{a_{k}}}_{k = 1}^{n}$

Figure 7. Iteration effect

图7. 迭代效果

例3：如(图8)所示的凸图形中取72个数据点以及每个点所对应权重大小，适当的调节对应点权重的

大小可以有更好的拟合效果。并用这些点来拟合平面 $y = \sin (\frac{u}{2}) con (\frac{v}{2})$ (如图9)中的一部分，其拟合效

果如图10所示。

Figure 8. Sampling points and weight distribution

图8. 取样点和权重分布

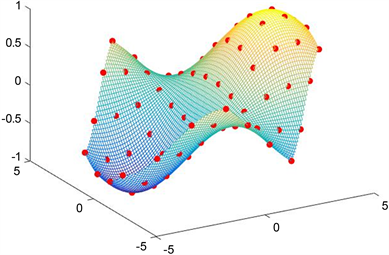
Figure 9. $f (u, v)$ and data point ${p_{a_{k}}}_{k = 1}^{n}$

图9. $f (u, v)$ 和数据点 ${p_{a_{k}}}_{k = 1}^{n}$

Figure 10. Iteration effect

图10. 迭代效果

5. 总结与展望

本篇文章定义了一种新的对凸多边形上的参数点进行字典排序的方法，方便对不规则凸多边形上的点进行排序与编号。并实现了一种用Toric曲面做渐进迭代逼近的算法。该方法可以直接逼近不规则的凸多边形域上的数据点，而无需考虑曲面的重构与拼接。相较于张量积Bézier曲面 [6] 和三角片面Bézier [4] [5] 曲面的渐进迭代逼近算法，本文的算法更加灵活，可以为任意凸多边形，所以适用场景更多。

总结研究成果，发现仍有以下问题可以进一步探讨：

1) Toric曲面的渐进迭代逼近收敛性是受toric-Bernstein基函数(公式1)中的自定义系数 $C_{i, j}$ 和Toric Bézier曲面(公式2)的权因子 $ω_{i, j}$ 影响的。给出Toric曲面渐进迭代逼近收敛的约束条件是我们进一步考虑的问题。

2) 矩阵B (矩阵3)为全正矩阵是渐进迭代收敛充分条件。如何在一定约束条件下证明(矩阵3)为完全正矩阵也是之后值得研究的问题之一。

文章引用

段卓,彭兴璇. Toric曲面的渐进迭代逼近
Progressive Iterative Approximation of Toric Surfaces[J]. 应用数学进展, 2023, 12(12): 5166-5174. https://doi.org/10.12677/AAM.2023.1212507

参考文献

1. 齐东旭, 田自贤, 张玉心. 曲线拟合的数值磨光方法[J]. 数学学报, 1975, 18(3): 173-184.

2. Lin, H.W., Wang, G.J. and Dong, C.S. (2004) Constructing Iterative Non-Uniform B-Spline Curve and Surface to Fit Data Points. Science in China Series: Information Sciences, 47, 515-331.

3. Lin, H.W., Bao, H.J. and Wang, G.J. (2005) Totally Positive Bases and Progressive Iterative Approximation. Computers and Mathematics with Applications, 50, 575-586. https://doi.org/10.1016/j.camwa.2005.01.023

4. 张莉, 李园园, 杨燕, 檀结庆. 三角域上Said-Ball基的推广渐近迭代逼近[J]. 中国图象图形学报, 2014, 19(2): 275-282.

5. 胡倩倩, 王家栋, 王国瑾. 三角B-B曲面最小二乘渐进迭代格式的革新与加速[J]. 计算机辅助设计与图形学学报, 2022, 34(5): 777-783.

6. Liu, C.Z., Liu, Z.Y., and Han, X. (2021) Preconditioned Progressive Iterative Approximation for Tensor Product Bézier Patches. Mathematics and Computers in Simulation, 185, 372-383. https://doi.org/10.1016/j.matcom.2021.01.002

7. 季康松, 寿华好, 刘艳. 带法向约束的隐式B样条曲线重构PIA方法[J]. 计算机辅助设计与图形学学报, 2023, 35(5): 719-725.

8. 吴硕琳, 李亚娟, 邓重阳. 基于PIA的非均匀三次B样条曲线Hermite插值[J]. 计算机学报, 2023, 46(11): 2463-2475.

9. 周晨, 陈伟, 刘渊. 基于渐进迭代逼近的矢量地图曲线化简方法[J]. 图学学报, 2021, 42(6): 979-986.

10. Krasauskas, R. (2002) Toric Surface Patches. Advances in Computational Mathematics, 17, 89-113. https://doi.org/10.1023/A:1015289823859

11. Sun, L.Y. and Zhu, C.G. (2015) Curvature Continuity Conditions between Adjacent Toric Surface Patches. Computer Aided Geometric Design, 37, 469-477. https://doi.org/10.1111/cgf.13583

12. Li, C.Y., Liu, H.Y. and Zhu, C.G. (2012) Constructing N-Sided Toric Sur-face Patches from Boundary Curves. Journal of Information and Computational Science, 9, 737-743.

13. 韩晓旭, 孙兰银, 朱春钢. 构造多管道过渡曲面的Toric曲面方法[J]. 计算机辅助设计与图形学学报, 2014, 26(10): 1639-1645.

14. 王涵, 朱春钢. 基于伸缩因子的Toric-Bézier曲线自由变形[J]. 图学学报, 2022, 43(6): 1070-1079.

15. 孙兰银, 朱春钢. 数据拟合的Toric Bézier曲面方法[J]. 数值计算与计算机应用, 2014, 35(4): 297-304.

16. Li, J.G. and Zhu, C.G. (2020) Curve and Surface Construction Based on the Generalized Toric-Bernstein Basis Functions. Open Mathematics, 18, 36-56. https://doi.org/10.1515/math-2020-0004

17. Yu, Y.Y., Ma, H. and Zhu, C.G. (2019) Total Positivity of a Kind of Generalized Toric-Bernstein Basis. Linear Algebra and its Applica-tions, 579, 449-462. https://doi.org/10.1016/j.laa.2019.06.012

NOTES

^*通讯作者。

期刊菜单