Advances in Applied Mathematics
Vol.
13
No.
04
(
2024
), Article ID:
85193
,
8
pages
10.12677/aam.2024.134133
偏多标记分类学习
王小碧
南昌航空大学数学与信息科学学院,江西 南昌
收稿日期:2024年3月19日;录用日期:2024年4月17日;发布日期:2024年4月24日

摘要
在偏多标记学习中,以往研究者常将偏多标记分类和标记消歧过程独立进行,并且未考虑标记相关性的先验知识难以事先获得。为此,本文提出了偏多标记分类和标记消歧联合学习的算法(JPMLLD)。JPMLLD建立一个从样本特征到标记的映射;其次通过将观测标记矩阵分解的方式进行消歧;最后建立了一个偏多标记分类和标记消歧统一的联合学习框架。大量实验结果验证了本文提出的JPMLLD算法的有效性。
关键词
偏多标记学习,标记相关性,特征选择,低秩表示,稀疏表示

Partial Multi-Label Classification Learning
Xiaobi Wang
School of Mathematics and Information Sciences, Nanchang Hangkong University, Nanchang Jiangxi
Received: Mar. 19th, 2024; accepted: Apr. 17th, 2024; published: Apr. 24th, 2024

ABSTRACT
In partial multi-label learning, researchers used to separate partial multi-label learning classification and label disambiguation processes, and prior knowledge without considering label correlation is difficult to obtain in advance. In this paper, we propose a joint learning method of partial multiple label classification and label disambiguation (JPMLLD). First, a mapping from sample features to labels is established. Secondly, the disambiguation is carried out by the decomposition of observation label matrix. Finally, a unified learning framework for partial multiple label classification and label disambiguation is established. The experimental results justify the effectiveness of the proposed JPMLLD algorithm.
Keywords:Partial Multi-Label Learning, Label Correlations, Feature Selection, Low-Rank Representation, Sparse Representation

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
现代社会中会产生大量的数据,同类数据之间会存在相似的特征,而现代人工智能具有强大计算和学习能力,利用机器可以将这些特征学习并且将学习的内容迁移到其他数据,帮助人类标记信息。多标记学习最初主要用于文档分类 [1] ,随后推广到各种各样的领域中,例如,由于蛋白质 [2] 、基因等生物学 [3] 领域的信息存在多义性,而机器学习非常适用于这种多义性信息的分析 [4] 。所以机器学习慢慢在生物学中得到应用。但是,现实生活中充斥大量信息,仅靠人工标注是非常费时费力的,大部分信息经人工标注后,训练者得到的是一个候选标记集,该候选标记集包括相关标记以及少量的不相关的噪声标记。这对以往的多标记学习提出了挑战,学者需要对这类问题进行研究,由此偏多标记学习(Partial Multi-label Learning, PML) [5] [6] 应运而生。PML主要是研究如何利用候选标记集和样本特征进行学习。
本文提出了基于矩阵分解的偏多标记学习方法。首先,建立一个从样本特征到标记的分类器,使每个标记不仅依赖样本特征也依赖其他标记;其次通过利用标记矩阵分解的方式进行消歧,最后建立了统一分类和消歧的学习框架。
本文的贡献在于:构建了一个偏多标记分类和标记消歧在统一框架下学习的偏多标记学习算法,丰富了偏多标记学习问题的研究。
2. 相关工作
如何消除噪声标记的影响是偏多标记的一个关键问题,研究人员将消除标记歧义的过程定义为消歧。已有许多学者研究出处理偏标记数据的消歧方法。有一部分学者 [7] 在处理候选标记时为每一个候选标记都赋予均等概率,采用监督学习的方式进行偏多标记学习。这种方式没有考虑候选标记中每个标记的差异性,消歧的效果容易受到假阳性标记干扰,真实标记被假阳性标记淹没。为了减轻平均消歧策略中的假阳性标记干扰的问题,有学者也提出使用加权平均 [8] 作为最终输出,研究者们提出了PL-KNN [9] 方法,根据距离远近对K近邻进行不同的权重赋值并按数值进行排序,排序最大作为真实标记。除此之外,有学者 [10] 提出通过最大似然估计进行学习,第一步消除候选标记集中的假阳性标签,第二步通过后验概率最大化得到真实标记。
3. 偏多标记分类学习
,这里的d是指特征的维度,n是指有n个训练示例,将 代表每个示例对应的标签,其中k是标签个数,矩阵里面的取值都是 ,比如,如果示例i具有标签j,那么 ,否则, ,则目标函数可以表示为:
为方便求解,我们将求T稀疏的秩转换为求T的核范数,将求E的0-范数转换成其相似的1-范数进行求解。
根据增广拉格朗日方法可变成:
由于1范数非凸,21范数是不可微,为求解式,为了便于表示,我们使用 来表示通过合并所有参数而形成的参数列向量,可将式子转换为两部分进行求解:
其中 目标函数 是两个函数的和,其中第一个函数 是凸光滑函数,第二个函数是1-范数和2-范数的和1范数是凸的,但不是光滑的。为了发展一种近似优化方法,我们考虑了目标函数 的二阶近似。对于任何L > 0,在一个给定的点 ,我们定义:
这里 是 在 在 的梯度函数。
设 表示 的Lipschitz常数。然后对于任何 ,有 ,基于Lipschitz常数的定义和 的凸性和光滑性 [11] [12] 。现在,我们假设 。根据 [13] 方法,我们有 。通过最小化 ,可以得到一个解决方法:
此时的 ,上述式子最小化可以等价地分解为一组独立的最小化问题,例如:
它们有封闭形式的解。其中稀疏范数凸优化问题的闭型解可以分别应用群软阈值和直接软阈值算子计算 [14] ,可得最终 更新公式:
其中◦表示元素向量乘积,算子 。
更新S,固定
求导可得:
更新b,固定
求导可得:
更新T固定
是一个非光滑凸问题,可以得到最优解。该定理 [15] 总结如下:
设 为 的奇异值分解(SVD),其中, 以及 为列正交矩阵, 为对角矩阵,其中, 。则通过求解以下方程,可以得到T的最优解:
为对角线矩阵和 。
4. 实验
4.1. 实验设置
实验共使用了九个网络公开数据集(六个ML数据集和两个PML数据)和六个对比算法。通过添加随机噪声方式,将每个多标记数据集生成多个带有候选标记的PML数据集 [16] 。具体地,在给定的多标记实例的标记集中添加不相关的标记生成合成PML数据集,通过改变候选标记的平均数量(#CLs)生成了21个合成PML数据集,表1总结了数据集的特征,包括特征数量,平均标记个数(#GLs)、平均候选标记个数(#CLs)和应用领域, 表示带有假阳性候选标记的个数。其中音乐情感、音乐风格为两个真实的PML数据集。
Table 1. Description of the multi-labeled dataset
表1. 多标记数据集的描述
本文对比了三种偏多标记算法和三种经典的多标记算法证明JPMLLD的有效性。
1) PML-LRS [17] 一种利用低秩矩阵分解将标记矩阵分解成真实标记和无关矩阵的偏多标记学习方法,该方法可以很好的去除噪声标记解决标记信息冗余等问题。
2) LIFT [18] 一种通过对每个正负标记进行聚类获取标记特征来训练分类器的偏多标记学习方法,该方法的特点是使用标记的特征来挖掘标记信息。
3) ML-KNN [19] 一种识别训练集k近邻获得每个可能类的相邻实例信息,通过最大后验来确定分类的懒惰学习算法,该方法在多标记学习中常作为对比算法。
4) PRATICLE [20] 是一种基于标记传播技术和k近邻信息来估计置信度矩阵的偏多标记学习方法,该方法通过阈值将置信度矩阵转化成标记矩阵,并基于成对排序模型在估计的标记矩阵上训练一个多标记分类器。
5) TRAM [21] 利用已知标记和未知标记获得有效模型的转换的一种多标记分类方法并提出了算法的封闭解,是一种可以通过标记集传播的多标记学习算法。
6) PLDA [22] 是一种研究偏多标记学习识别增强的算法,该方法提出了一种联合优化和估计部分标记置信度优化原型,同时保证特征全局和标记局部一致性。
4.2. 实验结果与分析
在进行对比实验时,本文使用60%的数据集进行训练,40%数据集用于测试,并采用随机10折交叉验证的方式进行训练。为了评估偏多标记分类器的性能,采用一种常见的评价准则 [16] [23] 进行评估比较,即Hamming Loss [24] ;对于Hamming Loss评估准则,值越小越优。表2详细记录了本文方法和其他六种方法在重复10次实验后得到的平均值和标准差。
Table 2. Performance comparison based on Hamming Loss (smaller value is better) on different labeled datasets
表2. 在不同标记的数据集上,基于Hamming Loss (值越小越好)的性能比较
从表2中数据可以看出,所有方法随着r的增加性能基本都会降低。在不同的r值情况下,JPMLLD在多数情况下优于其他算法。从表1的实验中可以看出,与其他方法相比,JPMLLD算法在12个数据集上的Hamming Loss值都大于其它算法,且在绝大多数数据集上相对稳定,对于Business数据集,JPMLLD的Hamming Loss值最大,对于Arts数据集,JPMLLD取得的平均结果最优。为了验证本文提出的算法是否与其它算法存在差异,在5%显著性水平的t检验上进行两两算法效果比较,并将结果表示在表2中。在表1中•表示本文的方法在统计t检验上优于比较方法,◦则表示比较方法优于本文的方法。
最后,采用显著性为5%的Nemenyitest [25] 进一步分析算法之间的差异,如两个算法之间差异显著,她们的实验结果排序值就不低于临界差(critical difference,简称CD),如图1所示,在每个子图CD在轴上方,排名越高效果越好的方法就越排在左边,没有显著差异的方法组用粗体实线连接。在图1中,JPMLLD与TRAM方法用CD线连接,说明基于Hamming Loss评价准则时,JPMLLD与TRAM方法性能相当,并且优于其他算法。
在所有21个实验中(包括评价指标以及不同数据集),JPMLLD在65%的实例中排名第一。值得注意的是,JPMLLD在所有评价中都达到了最优,这说明本文的方法拥有更好的性能。
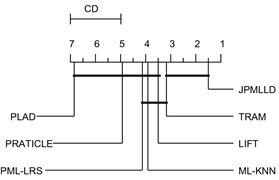
Figure 1. Performance comparison on classifier evaluation criteria
图1. 分类器评价准则上的性能比较
5. 结论
本文提出了一种基于矩阵分解偏多标记分类方法,通过低秩稀疏矩阵分解将标记矩阵分解成精确的标记矩阵和噪声标记矩阵的方式进行消歧;将问题可转化成一个凸优化问题,通过交替求解的方式进行求解,在9个数据集上基于Hamming Loss评价准则上的实验结果表明,JPMLLD优于其他6种算法。
文章引用
王小碧. 偏多标记分类学习
Partial Multi-Label Classification Learning[J]. 应用数学进展, 2024, 13(04): 1425-1432. https://doi.org/10.12677/aam.2024.134133
参考文献
- 1. 耿新, 徐宁. 标记分布学习与标记增强[J]. 中国科学: 信息科学, 2018, 48(5): 521-530.
- 2. 季小皖. 弱监督不平衡多标记分类方法研究[D]: [硕士学位论文]. 舟山: 浙江海洋大学, 2023.
- 3. 李鸿燕. 双因子张量范数正则化低秩张量填充[D]: [硕士学位论文]. 大连: 辽宁师范大学, 2023.
- 4. 薛鹏. 人体运动数据的特征表示与合成研究[D]: [硕士学位论文]. 南京: 南京信息工程大学, 2022.
- 5. 郝秀雁. 特征与标记同时缺失的多标记学习方法研究[D]: [硕士学位论文]. 马鞍山: 安徽工业大学, 2022.
- 6. 熊胤崧. 基于标记增强的特征选择及其在叶片种类识别中的应用研究[D]: [硕士学位论文]. 南昌: 江西农业大学, 2022.
- 7. 吕庚育. 弱监督多标记学习算法关键技术研究[D]: [硕士学位论文]. 北京: 北京交通大学, 2022.
- 8. 余婷婷. 噪声环境下的多标记学习方法研究与应用[D]: [硕士学位论文]. 重庆: 西南大学, 2021.
- 9. 孙利娟. 偏多标记学习算法关键技术研究[D]: [博士学位论文]. 北京: 北京交通大学, 2021.
- 10. 孙悦. 基于消歧策略的偏标记学习算法研究[D]: [硕士学位论文]. 北京: 北京交通大学, 2021.
- 11. 朱雯芳. 基于样本相关性的多标记学习算法及应用研究[D]: [硕士学位论文]. 南京: 南京理工大学, 2021.
- 12. Ming, K.X. and Sheng, J.H. (2021) Partial Multi-Label Learning with Noisy Label Identification. IEEE Transactions on Pattern Analysis and Machine Intelligence, 44, 3676-3687.
- 13. 谢明昆. 偏多标记学习研究[D]: [硕士学位论文]. 南京: 南京航空航天大学, 2021.
- 14. 宋帆. 基于专家的特征选择及缺省多标记学习策略[D]: [硕士学位论文]. 安庆: 安庆师范大学, 2020.
- 15. 李勇. 面向多标签决策系统的特征优化方法研究[D]: [硕士学位论文]. 北京: 中国石油大学(北京), 2020.
- 16. 杭仁龙. 遥感数据分析中的特征表示方法研究[D]: [硕士学位论文]. 南京: 南京信息工程大学, 2017.
- 17. 孙宁朝. 标注受限场景下的多标签学习方法研究[D]: [硕士学位论文]. 北京: 国防科技大学, 2020.
- 18. 张博文. 基于自适应近邻图模型与局部判别分析的特征选择算法研究[D]: [硕士学位论文]. 合肥: 安徽大学, 2020.
- 19. 王一宾, 吴陈, 程玉胜, 等. 不平衡标记差异性多标记特征选择算法[J]. 深圳大学学报(理工版), 2020, 37(3): 234-242.
- 20. 王雨思, 路德杨, 李海洋. 基于分式函数约束的稀疏子空间聚类方法[J]. 计算机工程与应用, 2020, 56(7): 39-47.
- 21. 王礼琴. 半监督多标记特征选择算法研究[D]: [硕士学位论文]. 长沙: 湖南师范大学, 2019.
- 22. 王恒远. 含噪数据的稀疏子空间聚类算法及理论研究[D]: [硕士学位论文]. 长沙: 西安工程大学, 2018.
- 23. 陈晓云, 廖梦真. 基于稀疏和近邻保持的极限学习机降维[J]. 自动化学报, 2019, 45(2): 325-333.
- 24. 曾玉华. 稀疏数据恢复的结构优化模型及其算法研究[D]: [硕士学位论文]. 长沙: 湖南大学, 2016.
- 25. 何志芬. 结合标记相关性的多标记分类算法研究[D]: [博士学位论文]. 南京: 南京师范大学, 2015.
