Hans Journal of Civil Engineering
Vol.
08
No.
02
(
2019
), Article ID:
29312
,
14
pages
10.12677/HJCE.2019.82044
Stability Analysis of a Pedestrian’s Walking Motion Based on the Inverted Pendulum Model
Yuke Fang, Bin Zhen, Lijun Ouyang, Tingting Li
School of Environment and Architecture, University of Shanghai for Science and Technology, Shanghai
Received: Feb. 28th, 2019; accepted: Mar. 13th, 2019; published: Mar. 20th, 2019

ABSTRACT
It is essential to understand dynamics of a pedestrian’s walking motion in the study of pedestrian-structure interaction. In this paper we investigate the stability of a pedestrian’s walking motion by using the inverted pendulum model with harmonic vibrations of the pivot point. Our theoretical research shows that not only the ratio between the lateral and vertical amplitudes, but also the ratio between the lateral and vertical frequencies of the pivot point has significant effects on the balance of the inverted pendulum. Numerical simulations are carried out to verify the correctness of theoretical analysis. Furthermore, according to comparison of stability conditions for different ratios between lateral and vertical frequencies, the reason why the ratio between the lateral and vertical frequencies is closed to 1/2 for a normal pedestrian is exposed. In many pedestrian-structure problems it is difficult to directly determine the forces induced by pedestrians. Our research indicates that it may be a novel idea by applying the inverted pendulum model to analyze dynamic interaction between pedestrians and a structure, which avoids the difficulty of determination of forces exerted by pedestrians.
Keywords:Inverted Pendulum Model, Pedestrian, Mathieu Equation, Stability
基于倒摆模型的行人行走的稳定性分析
房钰轲,镇斌,欧阳利军,李婷婷
上海理工大学环境与建筑学院,上海
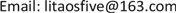
收稿日期:2019年2月28日;录用日期:2019年3月13日;发布日期:2019年3月20日

摘 要
人与结构的相互作用研究中必须弄清楚人行走的动力学行为。将人体视为倒摆,通过考虑倒摆支点的简谐运动来模拟人的行走行为,本文通过对倒摆模型的稳定性分析来讨论人行走的动力学行为。分析表明倒摆支点简谐运动的水平和竖直方向的振幅之比,频率之比都对倒摆的稳定性有重要影响。数值模型证实了本文采用的理论分析方法的正确性。比较倒摆支点在不同水平和竖直频率之比下的稳定性图谱可以解释为什么正常行走的行人通常都会保持水平和竖直行走步频之比在1/2附近,由此可以印证采用倒摆模拟行人行走的可行性。在许多人和结构相互作用问题的研究中往往较难确定行人产生的激励力大小。本文的分析表明可以考虑用支点做简谐运动的倒摆来模拟行人的行走,这可以避免直接确定行人激励力的困难。这可能为人与结构相互作用研究提供了一条新的思路。
关键词 :倒摆模型,行人,Mathieu方程,稳定性

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
人与结构之间的相互作用研究具有广泛的应用背景,如人与多层结构,人与网架结构,以及人与人行桥等。在这些研究中一个比较基本的问题是如何确定人产生的激励力。以人与人行桥相互作用的研究为例,在人–桥相互作用的研究中通常采用半经验的方法来确定行人产生的激励力的大小 [1] [2] [3] :根据对千禧桥的封闭测试,Dallard等 [4] 假设行人产生的侧向力和桥面运动的速度成正比。而Nakamura等 [5] 则认为仅当桥面运动的速度比较小时行人产生的侧向力与桥面的侧向速度成正比,当桥面的速度较大时行人产生的侧向激励力会趋向一个有限值而不会无限加大。Roberts [6] 认为人和桥之间的相互作用力总是简谐变化且频率总在1 Hz附近。尽管通过半经验方法得到的这些行人激励力的假设模型在实际应用中发挥了很大的作用 [7] [8] [9] ,但对机理性研究往往还不够深入。例如,为何人行桥的过大侧向振动总是集中在1 Hz附近,千禧桥中著名的跳跃现象的机理等,并不能根据这些经验侧向力模型得到很好的解释。因此有必要从理论上对行人产生的侧向力进行建模和分析。
当行人行走在静止的刚性平面上时由于身体的重心的振动会使得人在水平和竖直方向上都产生一个随着时间变化的激励力。正常行走时激励力主要集中在竖直方向,其大小在体重附近波动,而侧向力的大小约为体重的4%,频率为竖直方向步频的一半,约在0.7~1.2 Hz之间。在生物力学领域倒摆模型常用于研究人体的平衡性 [10] 。一些研究倾向于寻找能直接计算行人行走动力行为的公式 [11] ,而另外一些研究考虑用系统方法研究人体的姿态控制 [12] 。对人体进行真实的生物力学建模非常复杂,很难直接应用到人与结构的相互作用研究中。更为实际的做法是抓住人与结构相互作用过程中的主要特性,对行人的动力学建模进行简化。根据实验观察,Erlicher等 [13] 认为行人行走时身体具有自我保持性。在此观察基础上较为合理并可行的做法是将人体简化为倒摆。Macdonald [10] 采用倒摆模型模拟人的侧向力讨论了人–桥之间的相互作用,得到了和实测较为吻合的结果。在他们的研究中并未考虑倒摆支点的持续运动,因此无法讨论人的行走和行走过程中人体的稳定性。但这两点在人与结构相互作用的研究中往往非常重要,因为结构的振动会影响人的稳定性,而人体稳定性的改变又会影响到行走产生的激励力,从而反过来影响结构的振动。为更合理地用倒摆模型来模拟人的行走,本文考虑倒摆的支点在水平和竖直方向同时进行简谐运动。根据非线性动力学稳定性理论分析支点运动下倒摆的稳定条件,并在参数平面上利用摄动方法计算分界线(transition curves)的位置,由此讨论参数变化对行人行走稳定性的影响。我们的分析表明行人行走时水平和竖向方向步频之比,振幅之比都对人体的稳定性具有很大的影响,这和对行人正常行走的观测结果是吻合的。
本文剩下部分结构安排如下:在第二节中建立倒摆模型;在第三和四节中分别讨论倒摆系统的通解和稳定性分界线;在第五节中讨论参数变化对倒摆稳定性的影响;结论在第六节中给出。
2. 倒摆模型
本文用倒摆模拟行人在静止平面上的行走,如图1所示。摆球代表行人的质心,摆杆代表行人的腿。当人行走时质心上下左右波动,因此我们考虑摆杆的支点上下左右进行简谐运动来模拟人的行走。摆球的质量,摆杆的长度和支点竖向简谐运动的频率分别为m,L和ω。支点摆动的水平和竖直方向的幅值假设分别为A,B。n为水平和竖直振动频率的比值,ϕ为水平和竖直方向频率的相位差,g为重力加速度。图1中所示倒摆的控制方程可由Lagrange方法得到。假设
是摆杆运动时任意时刻与竖直方向所成的角度,
是为任意时刻倒摆支点的位置坐标,则总有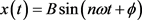 和
。摆球的位置坐标可以写为
。对位置坐标求导,可以得到摆球的速度
和
。摆球的位置坐标可以写为
。对位置坐标求导,可以得到摆球的速度

Figure 1. The diagram of the inverted pendulum model, in which the pivot point periodically moves up, down, left and right
图1. 倒摆模型,其中支点在水平和竖直方向做周期运动
。 (1)
倒摆系统的Lagrangian可以写为
, (2)
将(1)和(2)带入下面的Lagrange方程
,(3)
有
。 (4)
将时间重新标度 ,(4)可以写为
, (5)
其中,
, , 。
对于正常行走的行人 和 成立,所以 是一个小量。考虑到 ,(5)可以近似写为
。 (6)
3. 倒摆控制方程的通解
如果 ,(6)退化为
, (7)
因为 ,(7)没有周期解,如果 , 是唯一不稳定的平衡点。 意味着行人停止行走并保持站立。本文重点关注 , 附近(6)的解的稳定性。因此可以通过在(7)的解附近摄动来获得(6)的解。在 参数平面上,(7)的解稳定性区域由两条分界线包围而成,一条从 发出,而另一条从 发出。下面考虑(7)在 情况下如下形式的通解
。 (8)
将(8)带入(6)并且分别令 的各次幂系数为0,有
(9)
(9)中第一式的通解可以写为
, (10)
其中 ,a和b是依赖初始条件的常数。将(10)带入(9)的第二式,可以得到其特解
(11)
时(6)的二阶近似解可以写为
(12)
显然,系统(6)的共振条件为 和 (或者等价条件 和 )。当 时,系统(6)中出现强共振。四种不同参数情况下(12)的解析解和直接数值结果的比较结果如图2所示,表明了(12)的有效性。需要注意的是,当 增大时(12)的精度会下降,如果要提高精度,需要计算 的高阶项。
 (a)
,
,
,
,
(a)
,
,
,
,
 (b)
,
,
,
,
(b)
,
,
,
,
 (c)
,
,
,
,
(c)
,
,
,
,
 (d)
,
,
,
,
(d)
,
,
,
,
Figure 2. Comparison between analytical solution (···dot line) and the numerical solution (— solid line)
图2. 解析解(···点)和数值解(—实线)的比较
4. 分界线和周期解
在这一节中讨论 参数平面上(6)解的稳定性区域。根据上一节的讨论,稳定性区域由从δ-轴上 , 和 分别出发的分界线所包围而成。下面分别进行讨论。
首先假设参数δ能写成如下展开形式
, (13)
其中 是常数,可通过避免久期项来计算。将(8)和(13)带入(6)并且令 的各次幂系统为0,有
, (14)
, (15)
。 (16)
4.1. δ0 = 0
将 带入(14),有 ,其中 为常数依赖初始条件。此时(15)变为
。 (17)
如果令 为0, 是周期的。(17)的特解可以写为
。 (18)
将(18)带入(16)并消去久期项,有
(19)
从δ-轴上 点出发的分界线可以近似表示为
, (20)
分界线上的周期解可以解析地表示为
(21)
4.2. δ0 = n2 (n ≠ 1/2)
将 带入(14),得到(14)的通解
。 (22)
将(22)带入(15),(15)变为
。 (23)
要 为周期解,必须要消去久期项,因此有
(24)
a,b是任意依赖初始条件的常数,(24)的非平凡解可以写为
或者
4.2.1.
在这种情况下(23)的特解可以表示为
(25)
通过和前面相同的步骤,可以得到
(26)
此时分界线可以表示为
(27)
4.2.2.
在这种情况下分界线和分界线上的周期解可以分别表示为
(28)
(29)
4.3. δ0 = 1/4
和前面过程类似,可以分为两种情况,下面分别讨论。
4.3.1. a = b
在这种情况下分界线和分界线上的周期解可以分别表示为
(30)
(31)
4.3.2. a = −b
在这种情况下分界线和分界线上的周期解可以分别表示为
(32)
(33)
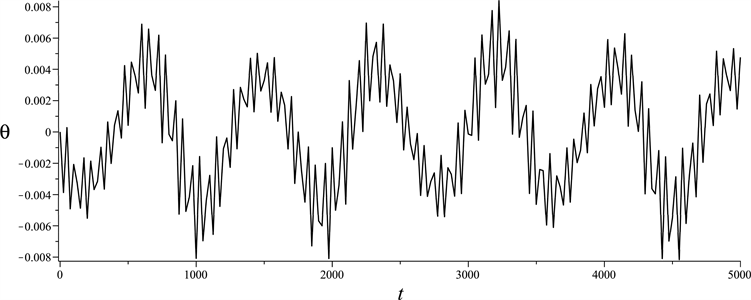
根据上面的解析表达式,在分界线上有无穷多的周期解。以从 出发的分界线为例,在(20)中令 ,则有 。另外,令 ,n = 0.4, ,并且取初始条件为 和 。直接采用数值方法对(6)进行积分得到倒摆摆角的时程图,相图和时程曲线的傅里叶谱,如图3所示。从图3(c)可以分辨出傅里叶谱中的频率分量为 ,这和解析解(21)的结果是吻合的。接下来选取 , , , , , ,此时(31)为近似解析解。直接对(6)进行积分得到时程图,相图和时程曲线的傅里叶谱,如图4所示。从图4(c)可以看到,周期解有频率分量 ,这和(31)的结果是吻合的。
5. 稳定性区域分析和讨论
本节中用(20),(27),(28),(30)和(32)来研究参数平面中的稳定性区域随参数改变的变化。令 , ,a和 的值分别为0.01,0.15,0.1,−0.2。n是倒摆支点水平与竖向振动频率之比。令n取0.25,0.45,0.55和0.75,在 参数平面上分别画相应的分界线并标注稳定性区域,如图5所示。从图中可以看出n值的变化对分界线以及稳定性区域都有很大的影响。在条件 和 下,如果 ,随着n值的增大参数平面上稳定性区域不断增加;但当 后n值再增加不会改变稳定性区域的面积。此外,当 时,稳定性区域是不连续的。图5表明 对于倒摆的稳定性而言是有利的。
 (a) The history time curves
(a) The history time curves
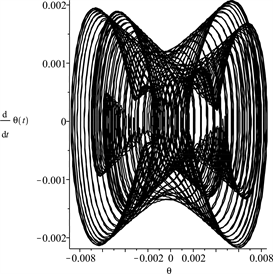
 (b) The phase-plane trajectory
(b) The phase-plane trajectory
 (c) The Fourier power spectrum
(c) The Fourier power spectrum
Figure 3. The direct numerical results for Equation (6) with δ = −0.02, , , n = 0.4 and , the initial conditions are taken as and
图3. (6)的数值积分结果,其中δ = −0.02, , ,n = 0.4, ,初始条件为 ,
 (a) The history time curves
(a) The history time curves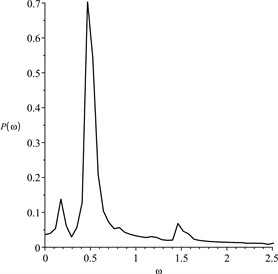 (b) The phase-plane trajectory
(b) The phase-plane trajectory  (c) The Fourier power spectrum
(c) The Fourier power spectrum
Figure 4. The direct numerical results for Equation (6) with δ = −0.02, , , n = 0.8 and , the initial conditions are taken as and
图4. (6)的数值积分结果,其中δ = −0.02, , ,n = 0.8, ,初始条件为 ,
 (a) n = 0.25
(a) n = 0.25  (b) n = 0.45
(b) n = 0.45 (c) n = 0.55
(c) n = 0.55 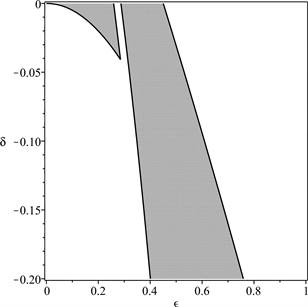 (d) n = 0.75
(d) n = 0.75
Figure 5. The stable regions (marked with grey shades) of solutions of Equation (6) under the conditions and δ < 0, in which , , a = 0.1, b = −0.2
图5. 参数平面上(6)的解的稳定性区域(用灰色标出),其中 , ,a = 0.1,b = −0.2, ,δ < 0
需要指出的是,当 时依赖初始条件的常数a和b都对稳定性区域的面积有影响。在对(6)直接数值积分时如果选择a = 0.5,b = −0.01,且其它参数与图6中保持一致,稳定性区域如图6所示。
对比图5和6,当 时初始条件对(6)的解的稳定性区域面积和连续性都有重要影响。而当 时,初始条件几乎不再有影响。
是倒摆支点水平和竖向振幅之比。为分析 对稳定性区域的影响,分别令 取0.05,0.1,0.15。其它参数和图5中参数保持一致。 对稳定区域的影响如图7所示。从图5和图7可以看出,当 时 对稳定性区域有很大的影响;当 时 的变化几乎没有影响。当 很小并接近0时, 时的稳定性区域的面积可能超过 时,但 时稳定性区域是不连续的(图5(b))。当 时,随着 的增加,稳定性区域的不连续性开始消失,稳定性区域的面积显著下降。对比图5和图7, 的增加总是使得不稳定性增加,此时不管n值的大小,通过减小 和δ来增加稳定性总是有效的。根据图5~7的分析对倒摆系统如果要获得好的稳定性需要 。
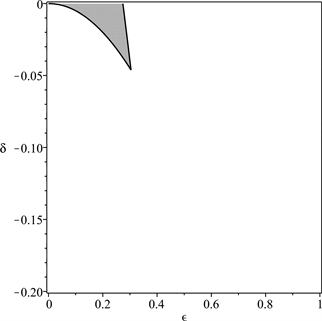 (a) n = 0.25
(a) n = 0.25 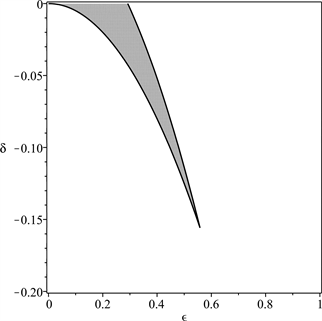 (b) n = 0.45
(b) n = 0.45 (c) n = 0.55
(c) n = 0.55  (d) n = 0.75
(d) n = 0.75
Figure 6. The stable regions (marked with grey shades) of solutions of Equation (6) under the conditions and δ < 0, in which , , a = 0.5, b = −0.01
图6. 参数平面上(6)的解的稳定性区域(用灰色标出),其中 , ,a = 0.5,b = −0.01, ,δ < 0
 (a)
, n=0.25
(a)
, n=0.25
 (b)
, n=0.25
(b)
, n=0.25
 (c)
, n=0.25
(c)
, n=0.25
 (d)
, n=0.45
(d)
, n=0.45
 (e)
, n=0.45
(e)
, n=0.45
 (f)
, n=0.45
(f)
, n=0.45
 (g)
, n=0.55
(g)
, n=0.55
 (h)
, n=0.55
(h)
, n=0.55
 (i)
, n=0.55
(i)
, n=0.55
 (j)
, n=0.75
(j)
, n=0.75
 (k)
, n=0.75
(k)
, n=0.75
 (l)
, n=0.75
(l)
, n=0.75
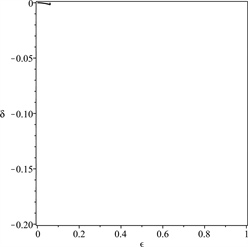
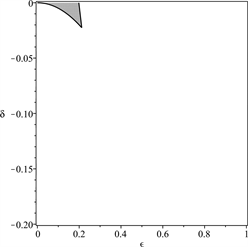
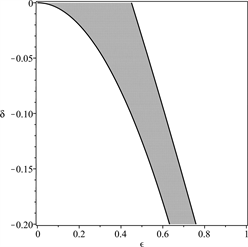
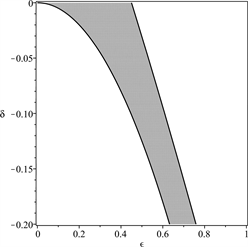
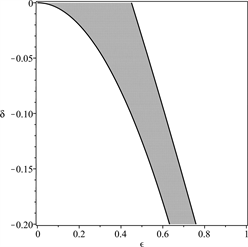
Figure 7. The stable regions (marked with grey shades) of solutions of Equation (6) under the conditions and δ < 0, in which , a = 0.1 and b = −0.2
图7. 参数平面上(6)的解的稳定性区域(用灰色标出),其中 ,a = 0.1,b = −0.2, ,δ< 0
考虑到真实行人的重心高度和竖向步频,重点关注δ的值在−0.03到−0.13范围内变化, 的值在0到0.4范围内变化。行人行走时重心上下振动,与此同时身体不可避免地会左右摇摆,因此侧向摆动幅度不会为0。根据上面对倒摆的稳定性分析,如果侧向步频与竖向步频之比小于1/2,身体保持稳定性的区域在参数平面上是不连续的。这意味着若要保持身体平衡可能需要不间断进行跳跃性调整,这对于行走而言是不合适的。因此从稳定性角度需要保持侧向和竖向步频之比大于1/2。而从能量消耗角度来看,步频之比大于1/2并不经济。因此,人行走时保持侧向和竖向步频之比在1/2附近是最为合理的。这和对行人行走时的观测结果是吻合的。另外,当行人的侧向和竖向步频之比小于1/2,则身体保持稳定所对应的参数区域的面积和连续性都极易被侧向和竖向步幅之比以及初始条件所影响。这可以用于解释为何一个喝醉的人或者刚开始学走路的婴幼儿非常容易摔倒。因为他们不能保证侧向步频与竖向步频之比足够大,并且难以及时调整步频和身体重心的高度。根据图5~7可以推知当行人的侧向摆幅比较大的,降低身体重心和加快竖向步频总可以有效地增强身体的平衡。这和对行人行走的实际观测是一致的。弯腰、快速调整落脚速度都是人体对脚下不稳情况下的自然反应。
6. 结论
本文采用倒摆模型研究行人行走的动力行为。考虑倒摆支点在水平和竖直方向做简谐运动来模拟行人行走时身体质心在侧向和竖向的起伏运动。利用摄动方法通过计算参数平面上的分界线得到了倒摆系统的稳定性条件,并用数值计算结果验证了理论分析的正确性。本文利用摆动稳定性分析论证了人行走时保持侧向和竖向步频之比在1/2附近是最为合理的。根据本文讨论,用支点作简谐运动的倒摆来模拟人的行走可以用于分析行人的动力学行为。通过将倒摆和结构耦合可以用于人–结构相互作用的分析,这可以避免直接确定行人产生的激励力带来的分析困难。这为理论分析人–结构耦合作用提供了一条新的思路。
基金项目
本文工作得到了国家自然科学基金项目(11472160, 51708349)的资助。
文章引用
房钰轲,镇 斌,欧阳利军,李婷婷. 基于倒摆模型的行人行走的稳定性分析
Stability Analysis of a Pedestrian’s Walking Motion Based on the Inverted Pendulum Model[J]. 土木工程, 2019, 08(02): 366-379. https://doi.org/10.12677/HJCE.2019.82044
参考文献
- 1. Ehsan, A., Colin, C., Stana, Z., Neil, E. and Amin, H. (2018) A Framework for Quantification of Human-Structure In-teraction in Vertical Direction. Journal of Sound and Vibration, 432, 351-372.
- 2. Van Nimmen, K., Lombaert, G., De Roeck, G. and Van den Broeck, P. (2017) The Impact of Vertical Human-Structure Interaction on the Response of Footbridges to Pedestrian Excitation. Journal of Sound and Vibration, 402, 104-121. https://doi.org/10.1016/j.jsv.2017.05.017
- 3. Maria, G.M., Eleonora, L. and Giulia, L. (2018) Coupled Analysis of Footbridge-Pedestrian Dynamic Interaction. Engineering Structures, 176, 127-142.
- 4. Dallard, P., Fitzpatrick, A.J., Flint, A., Le Bourva, S., Low, A., Ridsdill Smith, R.M. and Willford, M. (2001) The London Millennium Footbridge. Structure Engineering, 79, 17-33.
- 5. Nakamura, S. and Kawasaki, T. (2009) A Method for Predicting the Lateral Girder Response of Footbridges Induced by Pedestrian. Journal of Constructional Steel Research, 65, 1705-1711. https://doi.org/10.1016/j.jcsr.2009.03.003
- 6. Roberts, T.M. (2005) Lateral Pedestrian Excitation of Footbridges. Journal of Bridge Engineering, 10, 107-112. https://doi.org/10.1061/(ASCE)1084-0702(2005)10:1(107)
- 7. Erfan, S., Aleksandar, P. and Vitomir, R. (2017) Structural Vibration Serviceability: New Design Framework Featuring Human-Structure Interaction. Engineering Structures, 136, 295-311.
- 8. Xinxin, W., Van den Broeck, P., Guido, D.R. and Katrien, V.N. (2017) A Simplified Method to Account for the Effect of Human-Human Interaction on the Pedestrian-Induced Vibrations of Footbridges. Procedia Engineering, 199, 2907-2912. https://doi.org/10.1016/j.proeng.2017.09.331
- 9. Zhou, D., Han, H., Ji, T. and Xu, X. (2016) Comparison of Two Models for Human-Structure Interaction. Applied Mathematical Modelling, 40, 3738-3748. https://doi.org/10.1016/j.apm.2015.10.049
- 10. Macdonald, J.H.G. (2008) Lateral Excitation of Bridges by Balancing Pedestrians. Proceedings of the Royal Society of London A: Mathematical, Physical and Engi-neering Sciences, 465, 1055-1073.
- 11. De, H.M., Geurts, A.C., Dault, M.C., et al. (2005) Restoration of Weight-Shifting Capacity in Patients with Postacute Stroke: A Rehabilitation Cohort Study. Archives of Physical Med-icine & Rehabilitation, 86, 755-762. https://doi.org/10.1016/j.apmr.2004.10.010
- 12. Maurer, C. and Peterka, R.J. (2005) A New Interpretation of Spontaneous Sway Measures Based on a Simple Model of Human Postral Control. Journal of Neurophysiology, 93, 189-200. https://doi.org/10.1152/jn.00221.2004
- 13. Erlicher, S., Trovato, A. and Argoul, P. (2010) Modeling the Lateral Pedestrian Force on a Rigid Floor by a Self-Sustained Oscillator. Mechanical System and Signal Processing, 24, 1579-1604. https://doi.org/10.1016/j.ymssp.2009.11.006