Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30363
,
4
pages
10.12677/PM.2019.93056
Proof of No Odd Complete Number
Shanzhong Zou
Guangzhou Guangdong
Received: Apr. 26th, 2019; accepted: May 6th, 2019; published: May 22nd, 2019

ABSTRACT
The odd number is Q, Q = 2N + 1, and N is called odd element of Q. Through the analysis of N, it is proved that there is no odd complete number.
Keywords:Ontology of Odd Numbers, The Ontology of Compound Odd Numbers
证明无奇完全数
邹山中
广东 广州
收稿日期:2019年4月26日;录用日期:2019年5月6日;发布日期:2019年5月22日

摘 要
设奇数Q = 2N + 1,将N称为奇数Q的奇体,通过对N的分析证明了不存在奇完全数。
关键词 :奇体,奇合数体

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 奇合数体的表示法
设p是素数,Q与q是奇数,使
[1] ,若
,,,,,则有
,从而
。N称为奇合数体,可得定义1,奇合数体的表示法,
(1)
2. 命题证明
用反证法,假设存在奇完全数Q,
,,p是奇完全数Q的素数因子,
,把Q分为两个奇数的乘积,
,根据奇完全数的定义,有
,。
设,
,则有
。
即:
可得:
(2)
(2)式称为奇完全数的奇体表达式。由(2)可得推论一,N为偶数,t也是偶数。
证:若N为奇数,则
为奇数,而
为偶数,左右奇偶不合,故知
必为偶数,
是奇数,所以t必须是偶数。证明完。
,根据定义1,
,(
, )。
在
中,设
是Q中最小的素数,把
及
分别表为
, 可以依据组合
的不同,形成不同表达式。
将各种组合代入(2),有
上式简化后得:
(3)
要使(3)成立,必须满足
[2] 。
我们可以得到推论二,在
中,
或
,两者必取其一。
证,
,即:
,其中
和
可以表示为
, 证明完。
我们讨论当
时,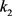 的取值。
的取值。
把
和
还原为Q,
,,
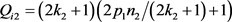 ,
是奇数,
应该是偶数,要使
,
是奇数,
应该是偶数,要使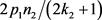 是偶数,必须满足以下条件:1)
,有
, 2)
有
,3)
有
:
是偶数,必须满足以下条件:1)
,有
, 2)
有
,3)
有
:
1)
,
不是整数,
当
时,
。
因此我们可以得到推论三,在
中,有
,即
。
证,如果
,则有
,使得
.,与推论三矛盾。证明完
2)
,即
,使等式成立。
t是偶数,设
,,满足等式,
,这样的结果与
相同,
,
3) 在
中,
不是整数,
必须是整数。
是Q中最小的素数,
,, 可以表示为
,,, 是Q中的素数。
,,,
设
,,有
,显然
,
(3)有:
,即
, 不是整数,
必须是整数,如果.
是整数,即
, (2)有:
使得
。
,即
, 不是整数
,即
。
,用Q中
逐个代入
,这使得
。
。
,, 不是整数,
必须是整数,
在能整除
的同时,
还必须整除
。
,这样便造成
, 当
时,因
无法取值,原假设不成立,所以不存在奇完全数。证明完!
文章引用
邹山中. 证明无奇完全数
Proof of No Odd Complete Number[J]. 理论数学, 2019, 09(03): 417-420. https://doi.org/10.12677/PM.2019.93056
参考文献
- 1. Gu, C.H. (1992) Mathematics Dictionary. Shanghai Dictionary Press, Shanghai.
- 2. Min, S.H. (1981) Method of Number Theory. Science Press, Beijing.
NOTES
作者简介:出生年月:1959年9月,籍贯:广东省始兴县,学历:本科,职称:工程师。





 的取值。
的取值。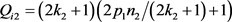 ,
是奇数,
应该是偶数,要使
,
是奇数,
应该是偶数,要使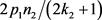 是偶数,必须满足以下条件:1)
,有
, 2)
有
,3)
有
:
是偶数,必须满足以下条件:1)
,有
, 2)
有
,3)
有
: