Pure Mathematics
Vol.
11
No.
04
(
2021
), Article ID:
42117
,
9
pages
10.12677/PM.2021.114079
具有状态切换的二人零和随机微分对策的 动态规划原理
李钧瑶
上海理工大学,上海
收稿日期:2021年3月20日;录用日期:2021年4月22日;发布日期:2021年4月30日

摘要
本文研究了具有状态切换的二人零和随机微分对策,主要结果是在倒向随机微分方程框架下具有状态切换的二人零和随机微分对策的动态规划原理。
关键词
随机微分对策,倒向随机微分方程,动态规划原理,状态切换
Dynamic Programming Principles for Two-Player Zero-Sum Stochastic Differential Games with Regime Switching
Junyao Li
University of Shanghai and Technology, Shanghai
Received: Mar. 20th, 2021; accepted: Apr. 22nd, 2021; published: Apr. 30th, 2021

ABSTRACT
In this paper, we study dynamic programming principles for two-player zero-sum stochastic differential games with regime switching. The main results of this paper concern dynamic programming principles with the help of the theory of backward stochastic differential equations.
Keywords:Stochastic Differential Games, Backward Stochastic Differential Equations, Dynamic Programming Principles, Regime Switching

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
自从Fleming和Souganidis [1] 的开创性工作以来,人们对随机微分对策进行了深入的研究。Buckdahn和Li [2] 利用倒向随机微分方程的方法考虑了具有非线性代价泛函的零和二人随机微分对策。由于具有表征各种随机事件的能力和易处理性,状态切换模型近年来受到人们的广泛关注。本文的主要结果是关于状态切换随机系统的二人零和随机微分对策的动态规划原理。
动态规划原则是解决最优控制问题最主要、也是最常用的方法之一,它意味着从今天来看的最优控制,在明天来看仍然是最优的,参见Fleming and Soner [3] 和Yong and Zhou [4]。该方法的基本思想是考虑一系列具有不同初始状态的最优控制问题,通过所谓的Hamilton-Jacobi-Bellman方程建立这些问题之间的联系。
本文的组织结构如下。在第2节中,我们将介绍一些符号和基本知识。在后文中将用到。在第三节中,我们将介绍动态规划原理。在第4节中,我们将讨论本文给出的结果的一些可能的应用。
2. 准备工作
设
是一个固定概率空间,其上定义了d维布朗运动
和马氏链
,其中
是从
到
的连续函数的集合,从0开始
, 是
上完备的Borel
-代数,P是维纳测度。这里我们假设
,其中
。令
表示布朗运动
产生的过滤。且
表示马氏链
生成的过滤。假设B和
是独立的。马氏链
取有限状态空间
中的值,是可观测的。马氏链
的生成元
由下式给出
其中
是从市场机制i到k的切换概率,对于每个
, 且
。
我们将在倒向随机微分方程的框架下,在有限时间范围内研究一个具有切换的两人零和随机微分对策。随机微分对策的动态由下面随机微分方程描述:对于
,
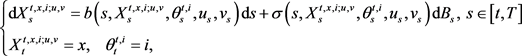 (2.1)
(2.1)
其中
为固定的有限时间范围,
视为初始状态,
。
是X在时间t的值,
是一对
适应的过程,它们在一些紧致度量空间U和V中取值,分别称为两个参与者I和II的容许控制。下面给出了系数
和
的精确假设。映射b和
满足下列条件:
(H2.1)
(i) 对于每一固定
, 和
是关于
连续的;
(ii) 对于任意
和
,存在一正的常数C使得,
从(H2.1)我们能够得到b和
的局部增长条件即,存在
使得,对于所有的
,,,,
如果上述假设成立,对于任意
和
,控制系统(2.1)有唯一解
。且我们有如下估计。
引理2.1. 在映射b和
的假设下,存在一常数
使得,对于任意
和
,
玩家的成本泛函由倒向随机微分方程:
(2.2)
给出,其中
和
是 给出的。上面的倒向随机微分方程有唯一一个解
。
我们现在给出两个函数
和端点成本函数
满足下面条件:
(H2.2)
(i) 对于任意固定的
, 是关于
连续的。
(ii) 存在
使得,对于所有
,,,,, 和
,
(iii) 存在
使得,对于所有的
,
在上面的条件下,我们有如下估计。
引理2.2. 对于所有的
,, 和
,存在一常数
使得,
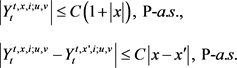 (2.3)
(2.3)
现在,我们介绍容许控制和容许策略。令
是两个确定时间,且
。
定义2.3. 对于玩家I (或者,player II)在时间
上取值于
(或者,
)的容许控制过程
(或者,
)关于滤波
是循序可测的。
在时间
上对于玩家I (或者,玩家II)的所有容许控制被定义为
(或者,
)。
定义2.4.在时间
上玩家Ⅰ的非预测性策略是一映射
使得,对于任意
-停时S和任意的
,如果在
上
(符号
)。同理,我们可以定义在
上玩家II的非预测性策略
。
在时间
上对于玩家I (或者,玩家II)的所有非预测性策略被定义为
(或者,
)。
对于给定的控制过程
和
,我们定义相关的成本泛函
其中,
是由倒向随机微分方程 定义的。在对策中,我们分别定义下值函数W和上值函数U,
和
上面的引理在 [5] 中已经被证明,只是随机微分对策的情况有一些差异。因此,参考 [5] 在本文的框架中,很容易得到上述结果。
引理2.5. 在假设(H2.1)和(H2.2)下,对于所有
,值函数
和
是确定性函数。
引理2.6. 在假设(H2.1)和(H2.2)下,对于所有
和
,我们有
对于函数U相同性质成立。
3. 动态规划原理
现在我们引入倒向随机半群,对于给定的初始状态
,我们定义了一个正数
,对于允许的控制过程
和
,以及一个实值随机变量
,我们定义
其中,
是下面倒向随机微分方程在端点时刻
的解,
且
是随机微分方程(2.1)的解。根据倒向随机微分方程解的唯一性,我们得到倒向随机微分方程(2.2)的解
满足
我们现在介绍具有状态切换的随机微分对策的值函数的动态规划原理。
命题3.1. 在假设(H2.1)和(H2.2)下,下面动态规划原理成立:对于所有
,,,
和
证明:令
我们将
与
相吻合的证明分几个步骤进行证明。
第一步.令
是任意固定的,则给定
,我们定义
在
的限制
如下:
其中
将
扩展为
中的一个元素。显然,
。且从
的非预测性性质,我们得到
独立于
的特殊选择。因此,从
的定义得
令
且对于一些序列
使得,
令
且设
。构造
,, 是
的一分割,且
。此外,从
的非预测性,我们得到
。由倒向随机微分方程的存在性和唯一性,得到对于
,
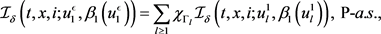
因此,
(3.1)
我们现在关注区间
,借助
不依赖于
,我们能定义
,对于任意
,从
可知,
属于
。因此,由
的定义知,对于任意的
使得,
从引理2.2和引理2.6,存在一常数
使得,对于任意
,,
(i)
(ii)
(3.2)
我们通过近似
来表示构造,
为了估计上面不等式的右边,我们注意到存在一些序列
使得
令
且
构造
, 是
一分割,此外,
。因此,从
的非预测性知,
,且由
的定义,我们得到
。由倒向随机微分方程的存在性和唯一性,我们知
因此,
(3.3)
其中
。从(3.1)和(3.3)可以知道,
(3.4)
因为
是任意选择的对于所有的
,我们有 。因此,
则令
,我们得到
。
第二步 我们现在处理
的情况。从
的定义,我们得到
且对于一些
使得,
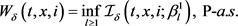
对于任意的
,我们令
, 且
, 是
的一分割,且
。由倒向随机微分方程的存在性和唯一性,我们得到对于所有的
此外,对于所有的
,
(3.5)
我们现在关注区间
,从
的定义,我们得到,对于任意
,存在
使得
(3.6)
我们现在考虑
的分割,即,
满足对于每一
,。令任意的
是固定的,且定义
显然,我们有
(3.7)
在
的每一处,对于任意的
。而且,对于每一个
和j,存在
使得 成立,且
现在我们定义新的策略
,其中
,。显然,
。
接下来,我们将证明
是非预测性的,实际上,令
是
-停时,
,使得
在
上。将
分解为
,使得
和
。因为在
上,
,我们有
在
上。另一方面,在
上
,且在
上,我们有
。因此,从定义知,在
上,
且在
上,
。所以,在
上,
从而知
。
固定
是任意的且分为
,,则从(3.5),(3.2) (i)和(3.7),我们知
从(3.6),(3.2) (ii)和(3.7)得,对于任意的
,
因此,
令
,我们有
。
证毕。
4. 总结
传统扩散模型相比,状态切换模型有两个明显的优点。首先,底层的马尔可夫链可以用来为具有长期系统影响的离散事件建模。其次,在进行数值实验时,状态切换模型只需要非常有限的数据输入。由于具有表征各种随机事件的能力和易处理性,状态切换模型近年来受到人们的广泛关注。本文的结果可以通过所谓的哈密顿雅可比–贝尔曼方程与一些最优控制问题联系起来。
文章引用
李钧瑶. 具有状态切换的二人零和随机微分对策的动态规划原理
Dynamic Programming Principles for Two-Player Zero-Sum Stochastic Differential Games with Regime Switching[J]. 理论数学, 2021, 11(04): 654-662. https://doi.org/10.12677/PM.2021.114079
参考文献
- 1. Fleming, W.H. and Souganidis, P.E. (1989) On the Existence of Value Functions of Two-Player, Zero-Sum Stochastic Differential Games. Indiana University Mathematics Journal, 38, 293-314.
- 2. Buckdahn, R. and Li, J. (2008) Stochastic Differential Games and Viscosity Solutions of Hamilton-Jacobi-Bellman-Isaacs Equations. SIAM Journal on Control & Optimization, 47, 444-475. https://doi.org/10.1137/060671954
- 3. Fleming, W.H. and Soner, H.M. (2006) Controlled Markov Processes and Viscosity Solutions. Springer, New York.
- 4. Jiong, M.Y. and Zhou, X.Y. (1999) Stochastic Controls: Hamiltonian Systems and HJB Equations. Springer Verlag, Berlin.
- 5. Buckdahn, R., Cardaliaguet, P. and Quincampoix, M. (2011) Some Recent Aspects of Differential Game Theory. Dynamic Games & Applications, 1, 74-114. https://doi.org/10.1007/s13235-010-0005-0





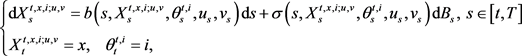 (2.1)
(2.1)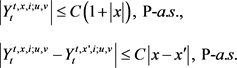 (2.3)
(2.3)