Operations Research and Fuzziology
Vol.
12
No.
03
(
2022
), Article ID:
54435
,
8
pages
10.12677/ORF.2022.123080
基于多目标优化的动态背包问题
赵俊如,王佳
福建师范大学数学与统计学院,福建 福州
收稿日期:2022年7月3日;录用日期:2022年8月1日;发布日期:2022年8月8日

摘要
优化问题和背包问题一直是科学研究领域的难点和热点问题。实际中很多优化问题都可以转化为背包问题,根据优化目标的非单一性,又可以提升复杂度,构造多目标背包问题。随着社会发展的复杂化趋势,使得这些问题迫切满足动态性,多约束等需求,因此动态背包问题逐渐成为新型研究主题的热点。本文通过结合多目标优化、动态背包问题的特点,提出了一个满足成本预算最低目标,客户满意度和车辆装载率最大目标的数学模型。并且对粒子群算法的特点进行了分析研究,然后利用多目标粒子群优化算法,对该动态背包问题进行了优化。为了验证模型的有效性和算法的效果与性能,利用随机产生的测试序列作为案例进行求解。
关键词
多目标优化,动态背包,粒子群

Dynamic Knapsack Problem Based on Multi-Objective Optimization
Junru Zhao, Jia Wang
School of Mathematics and Statistics, Fujian Normal University, Fuzhou Fujian
Received: Jul. 3rd, 2022; accepted: Aug. 1st, 2022; published: Aug. 8th, 2022

ABSTRACT
Optimization problems and knapsack problems have always been difficult and hot issues in the field of scientific research. In practice, many optimization problems can be transformed into knapsack problems. According to the non-singularity of the optimization objective, the complexity can be improved and a multi-objective knapsack problem can be constructed. With the complex trend of social development, these problems urgently meet the needs of dynamics and multiple constraints, so the dynamic knapsack problem is gradually becoming a hot topic of new research topics. By combining the characteristics of multi-objective optimization and dynamic knapsack problem, this paper proposes a mathematical model that satisfies the objective of minimum cost budget, maximum customer satisfaction and vehicle loading rate. The characteristics of particle swarm optimization are analyzed and studied, and the dynamic knapsack problem is optimized by using multi-objective particle swarm optimization algorithm. In order to verify the validity of the model and the effect and performance of the algorithm, the randomly generated test sequence is used as a case to solve.
Keywords:Multi-Objective Optimization, Dynamic Knapsack, Particle Swarm

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
工业中经常会需要解决多个目标的最佳设计方案和决策问题,这些问题必须满足多个原则或多设计条件。这类含有多目标和多约束的优化问题,称为多目标优化问题。多目标优化问题在工程应用等领域非常普遍并且处于非常重要的地位,自20世纪60年代早期以来,多目标优化问题吸引了越来越多不同背景研究人员的注意力。同时,多目标优化是最优化问题的一个重要分支,许多工程应用和科学研究的优化问题都可归纳为多目标优化问题。因此,解决多目标优化问题具有非常重要的科研价值和实际意义 [1] [2] [3] 。
一般情况下,多目标优化问题的各个子目标之间是矛盾的,一个子目标的改善有可能会引起另一个或者另几个子目标的性能降低,也就是要同时使多个子目标一起达到最优值是不可能的,而只能在它们中间进行协调和折中处理,使各个子目标都尽可能地达到最优化。其与单目标优化问题的本质区别在于,它的解并非唯一,而是存在一组由众多Pareto最优解组成的最优解集合,集合中的各个元素称为Pareto最优解或非劣最优解 [4] [5] 。
背包问题(简记为KP)是运筹学、计算机科学中的一个典型优化难题,有着广泛的实际应用背景。在理论上,尽管背包问题的结构简单,但它却具有组合爆炸的性质,在实际应用中,许多工业问题都可以用背包问题来描述求解,例如投资决策、货物装载、预算控制、作业调度等,并且还常作为其他问题的子问题被加以研究 [6] 。所以说,所有的整数规划问题都可以转化为背包问题,求解背包问题实际上就求解了所有的整数规划问题。如何将背包问题应用于实际问题中,并很好地解决实际问题,是研究学者不断思索、研究的一个领域。从这一方面来说,背包问题的模型改进以及算法实现,对复杂组合优化问题的进步是十分有益的。
背包问题也可以作为多目标优化问题,通常的做法是根据某效用函数或者是通过加权目标函数来将多目标化为单一目标来进行优化。但大多数情况下,在优化之前这种效用函数或者权重是难以明确的,为了使决策者深入掌握优化问题的特点,迫切需要提供多个解以便于做出合理的最终选择 [3] [7] [8] 。
2. 优化模型
多目标优化问题作为最优化问题的一个重要分支,虽然目前该领域有不少的研究学者,但是研究成果相对局限,仍有许多问题亟待解决。
2.1. 多目标优化模型
考虑由m个目标函数,n个决策变量以及任意约束条件组成的一般多目标优化问题,其数学表达如下:
(2.1)
其中 是n维决策变量, 定义了p个不等式约束, 定义了q个等式约束, 包括m个子目标函数。特别的,当 时,该模型转化为单目标优化问题。另外,决策变量的取值范围
(2.2)
取决于约束条件,称为可行域。且
(2.3)
是决策变量的定义范围,称为搜索空间。
对于某个 ,当不存在 ,使得 ,称x为问题(2.1)的Pareto最优解,也就是目标函数的最优解。
2.2. 背包问题的数学模型
2.2.1. 0~1背包问题
给定一个重量限制为b的背包,记物品的价值和重量分别为 ,变量
(2.4)
则典型的0~1背包问题的模型可以写成如下的0~1整数线性规划形式:
(2.5)
2.2.2. 多维背包问题
在0~1背包问题中,背包都只有一个限制,即携带物品总重量不能超过背包总载量。若物品装入到背包中,还需要考虑容量、价格等其他限制因素,此时问题转化为多维背包问题,又称为多约束背包问题。(同时若第i种物品的数量在理论上没有限制,此时的背包问题为无界多维背包问题。)设背包有d个限制,其限制量分别为 , 分别为第i类物品的价值, 分别为第i类物品的第j维属性的量,则其数学模型为:
(2.6)
3. 算法实现与模型求解
3.1. 多目标动态背包的数学模型
本文考虑的动态背包问题描述为:在满足配送车辆装载量、运输距离以及客户满意度的前提下,选择最优方案支配多辆配送车辆从一个配送中心出发,将货物送到多个配送点的每个终端客户中,使得配送过程中的配送距离与成本最低,客户满意度与车辆背包价值率最大。
该动态背包问题的目标函数有三个:配送成本,客户满意度,车辆平均载重率。其中客户满意度是客户针对货物配送过程中质量的总体评价,本文主要体现于动态时间窗方面,假设货物配送时间为t,则客户满意度函数为 ,具体表达式如下:
(3.1)
其中 , 分别是货物配送至配送点i客户所能接受的最早时间和最迟时间,式(3.1)中,在时间段 内,客户满意度最佳。假设配送点i的货物需求量为 ,则 表达式所呈现的关系见图1:

Figure 1. Schematic diagram of customer satisfaction function
图1. 客户满意度函数示意图
根据以上的分析,具体的动态背包多目标优化问题模型可以定义如下:
(3.2)
(3.3)
(3.4)
(3.5)
(3.6)
(3.7)
(3.8)
模型中,I,J,K分别是配送点,货物以及不同载重量的车辆种类,i,j,k为对应编号; 为第k辆装载货物j的单价, 为配送中心至配送点i的距离, 为货物j的重量, 为第k类车辆的额定装载量。式(3.2)~(3.4)分别表示配送成本目标函数,客户满意度目标函数,平均载重率目标函数;式(3.5)~(3.8)为模型的约束条件。
3.2. 多目标粒子群优化算法
动态背包问题属于典型的NP问题,解决这类优化问题的算法包括精确算法、近似算法、启发式算法与元启发式算法。精确算法一般只应用于规模较小的问题,当问题规模较大是,常用来为启发式算法提供初始解,一边搜索到更好的解 [9] [10] [11] 。
当前求解多目标优化问题时,进化算法已经得到广泛应用,尤其是基于Pareto支配的进化多目标优化方法,其优化性能在大规模数据系统优化问题中得到充分体现。所以本文将根据多目标动态背包优化问题的特点,结合基于Pareto支配的粒子群算法(PSO),即多目标粒子群算法(MOPSO)对其进行求解。
在PSO优化模型中,每个粒子具有当前位置和当前速度的属性,记为 。粒子通过比较自身的最有位置 和整个群体的最有位置 ,及下列方程来更新自己的位置和速度 [7] [8] [9] :
(3.9)
(3.10)
其中 , 分别是第i个粒子的原来速度和当前速度; , 分别是第i个粒子的当前位置和产生的新位置, , 为正常数,又称为学习因子; , 是 范围内的随机数, 为惯性因子,通常取值于 范围。
在利用MOPSO求解的过程中,由于ST (存储列表)中的值是不断更新的,根据通过检查粒子当前解在种群中的优劣关系,并将得到的非支配解储存在ST,从而优化算法性能。具体的求解优化过程见图2:
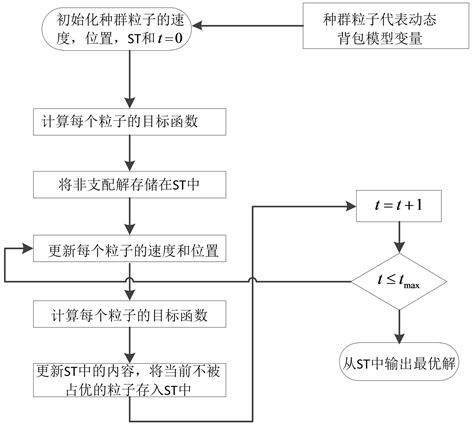
Figure 2. The flow of multi-objective particle swarm algorithm
图2. 多目标粒子群算法的流程
3.3. 模型求解
本文通过随机方法构造测试列,生成一个具有10个配送点,10个货物,10种类型的装运车辆的模型数据,具体见表1~4:
Table 1. The unit price of different goods delivered by each vehicle
表1. 各车辆运送不同货物的单位价格
Table 2. Distance from distribution center to 10 distribution points
表2. 配送中心距离10个配送点的距离
Table 3. Ten cargo weight
表3. 10个货物的重量
Table 4. Rated load capacity for ten types of vehicles
表4. 10种类型车辆的额定装载量
在该配送系统下,输入客户可接受的时间窗,利用基于Pareto支配的多目标粒子群算法求解动态背包模型,根据多目标优化求解结果可知,借助python通过上述模型与算法进行求解,多目标优化问题得到的是一组Pareto优化解,见图3和表5:

Figure 3. Cost objective function solution result and particle motion state
图3. 成本目标函数求解结果及粒子运动状态
图3显示的是最低成本目标函数的寻优过程,左边使用turtle动态显示粒子的解和当前历史最优解,右边显示的是最优解的背包价值的变化及粒子的运动过程。
Table 5. System resulting data of standard experiment
表5. 标准试验系统结果数据
根据上表所示结果,Pareto最优解所对应的配送方案为实际的终端配送方案。同时,Pareto最优解中并不是所有的目标函数值达到最优,而是根据对应决策变量的所有的目标函数的关系来确定是否为非支配解 [6] 。
4. 总结
本文以动态背包问题的优化为目标,探讨了一个包含多个目标的动态背包模型的构建过程,在粒子群算法的基础上,结合多个目标,利用Pareto对模型的多个目标函数进行优化。并利用随机产生的测试序列作为案例进行求解,得到最优解,即最优的配送方案,验证了算法对该模型的有效性。
本文模型能实现物流订单配送,车辆调度,客户满意度预测等功能,今后的研究工作可以考虑更多的动态因素,如延迟率、实时订单变化等。
基金项目
国家自然科学基金面上项目(11671335);福建省自然科学基金项目(2021J01660)。
文章引用
赵俊如,王 佳. 基于多目标优化的动态背包问题
Dynamic Knapsack Problem Based on Multi-Objective Optimization[J]. 运筹与模糊学, 2022, 12(03): 759-766. https://doi.org/10.12677/ORF.2022.123080
参考文献
- 1. 周焰梅. 基于群智能算法的动态物流背包研究与应用[D]: [硕士学位论文]. 重庆: 重庆邮电大学, 2019.
- 2. 林百川. 求解动态约束背包问题的改进原对偶遗传算法研究[D]: [硕士学位论文]. 沈阳: 东北大学, 2017.
- 3. 付源翼. 一种动态多目标背包问题及其算法研究[D]: [硕士学位论文]. 沈阳: 东北大学, 2017.
- 4. 王丰丰. 求解动态优化问题的遗传算法的研究与实现[D]: [硕士学位论文]. 上海: 上海交通大学, 2010.
- 5. 贺毅朝, 宋建民, 张敬敏, 苟海燕. 利用遗传算法求解静态与动态背包问题的研究[J]. 计算机应用研究, 2015, 32(4): 1011-1015.
- 6. 李哲以. 快递物流配送中背包问题优化算法的研究[D]: [硕士学位论文]. 重庆: 重庆邮电大学, 2017.
- 7. 吴亚丽, 徐丽青. 一种基于粒子群算法的改进多目标文化算法[J]. 控制与决策, 2012, 27(8): 1127-1132.
- 8. 李纬, 张兴华. 一种改进的基于解的多目标粒子群算法[J]. 计算机仿真, 2010, 27(5): 96-99.
- 9. 王佺, 聂仁灿, 周冬明, 金鑫, 贺康建, 余介夫. 多目标粒子群优化参数的图像融合算法[J]. 中国图象图形学报, 2016, 21(10): 1298-1306.
- 10. Gordon, V. and Whitley, D. (1993) Serial and Parallel Genetic Algorithms as Function Optimizers. Serial and Parallel Genetic Algorithms as Function Optimizers. In: ICGA, 177-183.
- 11. Zouache, D., Moussaoui, A. and Abdelaziz, F.B. (2018) A Cooperative Swarm Intelligence Algorithm for Multi-Objective Discrete Optimization with Application to the Knapsack Problem. European Journal of Operational Research, 264, 74-88. https://doi.org/10.1016/j.ejor.2017.06.058
