Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:19124,8
pages
10.12677/AAM.2016.54091
Quantum Measurement of PT-Symmetric Quantum Theory
Lili Yang, Zhengli Chen, Haipeng Sun
School of Mathematics and Information Science, Shaanxi Normal University (SNNU), Xi’an Shaanxi

Received: Nov. 11th, 2016; accepted: Nov. 26th, 2016; published: Nov. 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Quantum computer is a kind of physical device which carries out mathematical and logical calculations, and stores and manages the quantum information efficiently under the rule of the quantum mechanics. Quantum measurement is an important research topic in quantum information and quantum computing realm, however, the relative research has not appeared in the PT-symme- trical quantum system. In this paper, we give the general concept of quantum measurement in the PT-symmetrical quantum system. Moreover, the detailed discussion is described by using the methods of matrix and operation theory, and we obtain two results about quantum measurement in the PT-symmetrical quantum system.
Keywords:PT-Frame, PT-Symmetry, CPT-Frame, States, Measurement

PT-对称量子理论中的量子测量
杨丽丽,陈峥立,孙海鹏
陕西师范大学数学与信息科学学院,陕西 西安

收稿日期:2016年11月11日;录用日期:2016年11月26日;发布日期:2016年11月30日

摘 要
量子计算机是一类遵循量子力学规律进行高速数学和逻辑运算、存储及处理量子信息的物理装置,量子测量是量子信息和量子计算中的一类重要研究课题,但是在PT-对称量子系统中还没有相关的研究。本文给出PT-对称量子系统中一般量子测量的概念,并运用矩阵和算子论的方法,对这个问题进行了详细的讨论,得到了PT-对称量子系统中关于量子测量的两个结果。
关键词 :PT-框架,PT-对称,CPT-框架,态,测量

1. 引言
量子力学的四个假设把物理世界与量子力学的数学描述联系了起来,其中假设3为描述量子系统的测量提供了一条途径 [1] 。假设3说:量子测量由一组测量算子 描述,这些算子作用在被测量系统状态空间上,指标
描述,这些算子作用在被测量系统状态空间上,指标 表示实验中可能的测量结果。若在测量前,量子系统的最新状态是
表示实验中可能的测量结果。若在测量前,量子系统的最新状态是 ,则结果
,则结果 发生的可能性由
发生的可能性由 给出,且测量后系统的状态为:
给出,且测量后系统的状态为:

测量算子满足完备性方程:

假设3的一个重要应用就是区分量子状态。经典世界里,研究对象的不同状态至少原则上常常是可以区分的。例如文献 [1] 中所述:我们至少可以在理想情况下知道硬币是正面还是反面向上,而在量子力学中,情况就比较复杂。
华盛顿大学的C. M. Bender教授在1998年创立了PT-对称量子力学。PT-对称量子力学是将薛定谔方程中的哈密尔顿量H的“自伴性”条件用“H具有PT-对称性”来替代而产生的量子力学。其中算子H具有PT-对称性是指它与算子PT可交换。该理论是经典量子理论的复化,特别是该理论将H的自伴性这一数学条件物理化。PT-对称理论在光学实验中得到了验证。PT-对称理论极大拓广了经典量子力学的应用范围,它具有真实的物理意义与背景 [2] [3] [4] ,得到了国外学者的广泛关注 [5] - [13] 。PT-对称量子理论研究的是量子系统在空间对称变换和时间反演变换下的对称性 [11] 。
与经典量子力学相比,在PT-对称量子理论中,哈密顿量H的自伴性不再是必须要求。许多专家学者已给出了PT-对称量子系统中在有限维Hilbert空间上非自伴的Hamiltonian H的形式,也已经定义出了 和
和 这两种时间反演下的PT内积、CPT内积,但是关于PT-对称量子系统中的量子测量还没有给出,这正是本文要研究的内容。
这两种时间反演下的PT内积、CPT内积,但是关于PT-对称量子系统中的量子测量还没有给出,这正是本文要研究的内容。
2. PT-对称性
经典量子力学的动力学性质通过以下的薛定谔方程描述:
 ,
, 。
。
其中 表示系统的状态,称为波函数,
表示系统的状态,称为波函数, 为复Hilbert空间
为复Hilbert空间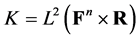 中的稠定自伴算子(称为哈密尔顿量算符),
中的稠定自伴算子(称为哈密尔顿量算符), 为实数域或复数域。
为实数域或复数域。
PT对称理论研究的是量子系统关于“空间对称变换”与“时间反演变换”的对称性。这两种变换是状态空间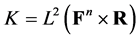 上的两个算子
上的两个算子 与
与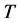 ,它们的定义是
,它们的定义是

显然,它们都连续的,空间对称变换 是线性的、时间反演变换
是线性的、时间反演变换 是共轭线性的(或称反线性的)。同时,
是共轭线性的(或称反线性的)。同时, 。
。
定义2.1 [11] 如果量子系统(2.1)的哈密尔顿量算符 与算子
与算子 可交换,即
可交换,即
 ,
,
则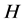 称为是
称为是 -对称的。此时,也称系统(2.1)是
-对称的。此时,也称系统(2.1)是 -对称的。
-对称的。
定义2.2 [11] 设 是Hilbert空间
是Hilbert空间 上的线性算子满足
上的线性算子满足 (恒等算子),
(恒等算子), 是
是 上的反线性(又称共轭线性)算子,满足
上的反线性(又称共轭线性)算子,满足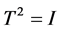 且
且 。空间
。空间 中的线性算子
中的线性算子 称是PT-对称的(或称
称是PT-对称的(或称 具有
具有 -对称性),如果
-对称性),如果 且与
且与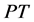 可交换:
可交换: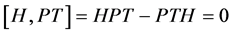 (在
(在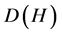 上成立),等价地,
上成立),等价地, 。如果记
。如果记 ,那么
,那么 是PT-对称的当且仅当
是PT-对称的当且仅当 。
。
定义2.3 [11] 设 上复Hilbert空间
上复Hilbert空间 上的算子,满足以下条件:
上的算子,满足以下条件:
(1) 是恒等的线性算子,
是恒等的线性算子,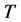 是共轭线性算子;
是共轭线性算子;
(2)  (K上的恒等算子);
(K上的恒等算子);
(3) ;
;
则称算子组 为
为 上的一个
上的一个 -结构。又若
-结构。又若
(4) 为线性算子,
为线性算子, ,
, ;
;
(5) 关于
关于 上的原来内积是正定的:即
上的原来内积是正定的:即 ,且
,且
 ,
,
则称算子组 为空间
为空间 上的一个
上的一个 结构。又若
结构。又若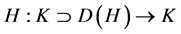 为线性算子,且
为线性算子,且
(6) ,即
,即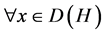 ,有
,有 ,则称算子组
,则称算子组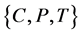 为算子
为算子 的一个
的一个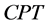 -框架。
-框架。
3. PT-对称量子系统中的量子测量
在经典量子系统中的量子测量在假设3中已经给出,那么在PT-对称量子系统中量子态的测量又是什么样的呢?在本节中我们将讨论这个问题。
在PT-对称量子系统中,设量子测量由一组测量 描述,若在测量前,量子系统的最新状态是
描述,若在测量前,量子系统的最新状态是 ,则结果
,则结果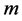 发生的可能性由:
发生的可能性由:

给出,且测量后系统的状态为:
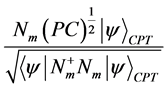
测量算子满足方程: 。
。
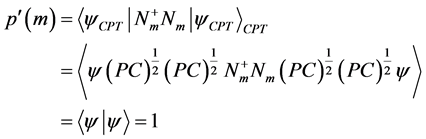
定理1设 ,
,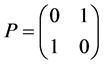 ,
, ,
,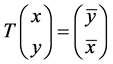 ,
,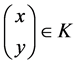 。
。 ,
, 。则
。则 是
是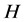 的一个CPT-框架,而且
的一个CPT-框架,而且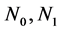 为这个PT-对称量子系统的一组测量算子。
为这个PT-对称量子系统的一组测量算子。
证明 (1)
 ,
, 。即
。即 。
。
 。
。
 ,
, ,即
,即 。
。
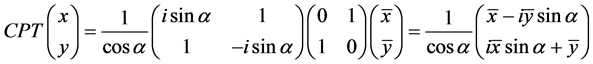 。
。
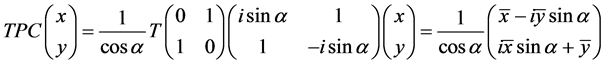 。
。
即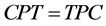 。设
。设 ,则
,则
 。
。
且

所以 是
是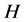 的一个CPT-框架。
的一个CPT-框架。
(2) 因为
 ,
, 。
。
所以
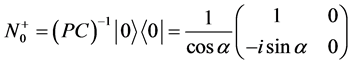 ,
,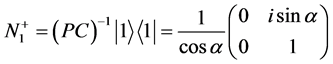 。
。
从而
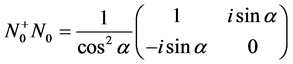 ,
,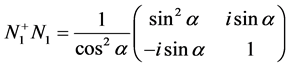 。
。
而且
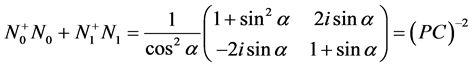 。
。
因此
 ,
,

从而 为这个PT-对称量子系统的一组测量算子。
为这个PT-对称量子系统的一组测量算子。
注 对于上面的测量算子 ,设被测量状态是
,设被测量状态是

则获得测量结果0的概率为

获得测量结果1的概率为
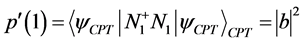
测量后的状态分别为: ,
,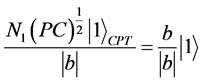 。
。
定理2设
 ,
, ,
,
 ,
, ,
, ,
,
 ,
, ,
, ,
,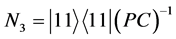 ,则
,则 是
是 的一个CPT-框架,而且
的一个CPT-框架,而且 为这个PT-对称量子系统的一组测量算子。
为这个PT-对称量子系统的一组测量算子。
证明 (1)
 ,
, ,即
,即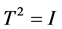 。
。
 。
。
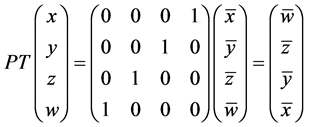 ,
, 。
。
即 。
。
 。
。
 。
。
即 。设
。设 ,则
,则
 。
。
且

所以 是
是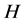 的一个CPT-框架。
的一个CPT-框架。
(2)
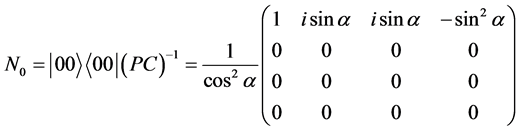



则
 ,
, ,
, ,
,
且

得

从而 为这个PT-对称量子系统的一组测量算子。
为这个PT-对称量子系统的一组测量算子。
4. 结论
本文得出了在PT-对称量子系统中的量子测量,即量子测量由一组测量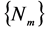 描述,测量后系统的状态为:
描述,测量后系统的状态为: 。并且通过两组测量算子
。并且通过两组测量算子 ,
, 和
和 ,
, ,
, ,
, 得到了PT-对称量子系统中关于量子测量的两个结果。
得到了PT-对称量子系统中关于量子测量的两个结果。
基金项目
国家自然科学基金(批准号:11571213)。
文章引用
杨丽丽,陈峥立,孙海鹏. PT-对称量子理论中的量子测量
Quantum Measurement of PT-Symmetric Quantum Theory[J]. 应用数学进展, 2016, 05(04): 790-797. http://dx.doi.org/10.12677/AAM.2016.54091
参考文献 (References)
- 1. Nielsen, M.A. and Chuang, I.L. 量子计算和量子信息 [M]. 赵平川, 译. 北京: 清华大学出版社, 2004: 79-81.
- 2. Bender, C.M., Boettcher, S. (1998) Real Spectra in Non-Hermitian Hamiltonians Having PT-Symmetric. Physical Review Letters, 80, 5243-5246. https://doi.org/10.1103/PhysRevLett.80.5243
- 3. Bender, C.M. (2005) Introduction to PT-Symmetric Quantum Theory. Contemporary Physics, 46, 277-292. https://doi.org/10.1080/00107500072632
- 4. Bender, C.M. and Wu, J.D. (2012) PT-symmetric Scientic. Mathematics of Operations Research, 2, 1-6.
- 5. Bender, C.M., Brody, D.C. and Jones, H.F. (2002) Complex Extention of Quantum Mechanics. Physical Review Letters, 89, 617-628. https://doi.org/10.1103/PhysRevLett.89.270401
- 6. Bender, C.M. and Klevansky, S.P. (2010) Families of Particles with Different Masses in PT-Symmetric Quantum Field Theory. Physical Review Letters, 105, 031601. https://doi.org/10.1103/PhysRevLett.105.031601
- 7. Croke, S. (1973) PT-Symmetric Hamiltonians and Their Application in Quantum. Physical Review A, 91, 052113. https://doi.org/10.1103/PhysRevA.91.052113
- 8. Wang, Q., Chia, S. and Zhang, J. (2010) PT-Symmetric as a Generalization of Hermiticity. Journal of Physics A: Mathematical and Theoretical, 43, 38FT02.
- 9. Chen, S.L., Chen, C.Y. and Chen, Y.N. (2014) Increase of Entanglement by Local PT-Symmetric Operation. Physical Review Letters, 90, 054301.
- 10. Leclerc, A., Viennot, D. and Jolicard, G. (2012) The Role of the Geometric Phases in Adiabatic Population Tracking for non-Hermitian Hamiltonians. Journal of Physics A: Mathematical and Theoretical, 45, 444015.
- 11. Cao, H.X., Guo, Z.H. and Chen, Z.L. (2013) CPT-Frames for Non-Hermitian Hamiltonians. Communications in Theoretical Physics, 60, 328-334. https://doi.org/10.1088/0253-6102/60/3/12
- 12. 段媛媛, 刘晓华, 陈峥立. 关于PT-对称的一些研究[J]. 纺织高校基础科学学报, 2013(26): 441-444.
- 13. 刘晓华, 陈峥立, 段媛媛. PT-对称中量子态的区分[J]. 计算机工程与应用, 2013, 51(7): 61-63.