Advances in Applied Mathematics
Vol.
12
No.
02
(
2023
), Article ID:
61920
,
6
pages
10.12677/AAM.2023.122074
一类连通图的Tutte多项式
祁禄
辽宁师范大学,辽宁 大连
收稿日期:2023年1月26日;录用日期:2023年2月21日;发布日期:2023年2月28日

摘要
近年来,随着拓扑学家对纽结理论的深入研究,空间图理论逐渐成为学者们的研究热点。Tutte多项式在空间图理论中具有重要地位,本文利用缩边与减边的性质,借助二元的数学归纳法计算了一类连通图的Tutte多项式,最终得出这类连通图的Tutte多项式。
关键词
Tutte多项式,二元数学归纳法, 图

The Tutte Polinomials of a Kind of Connected Graphs
Lu Qi
Liaoning Normal University, Dalian Liaoning
Received: Jan. 26th, 2023; accepted: Feb. 21st, 2023; published: Feb. 28th, 2023

ABSTRACT
In recent years, with the in-depth research of mathematicians in the field of topology, spatial graph theory gradually becomes a hot topic for scholars. The Tutte polynomials occupy a central place in spatial graph theory. In this paper, we calculate the Tutte polynomials of a kind of connected graphs by quality of edge and Mathematical induction of two variables, lastly, we get the Tutte polynomials of this kind of connected graphs.
Keywords:Tutte Polynomial, Mathematical Induction of Two Variables, Graph

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Tutte多项式是空间图多项式不变量的一个重要代表,Tutte多项式包含了图的大量信息 [1] ,由Tutte多项式可以得到图的生成森林数、连通子图数、无圈定向数等 [2] ,且由Tutte多项式可以得到链多项式、Flow多项式等图的多项式不变量 [3] 。近年来,学者们提出了许多关于Tutte多项式的研究课题,Doslic直接利用Tutte多项式删边与减边的性质计算出书图的具体表达式 [4] ,Brennan利用生成函数的方法计算出扇图的Tutte多项式 [5] ,廖云华利用生成子图展开定义得到了几类网格图的Tutte多项式,并且通过计算出其某些特殊点的值来得到图的重要参数 [6] 。Kung从多角度对Tutte多项式进行阐述 [7] 。
本文计算一类图的Tutte多项式,共分为两部分,第一部分介绍了相关的基础知识,在第二部分中,首先计算得到图 的Tutte多项式。在此基础上,计算得到图 的Tutte多项式。
2. 预备知识
2.1. 图
定义1.1将有序三元组 称作图,记为G。将 记为图G的顶点集, 记为图G的边集,并且 , 将G的每条边对应G的定点对(顶点可以是同一个)。若边e与两个顶点 满足 ,则称顶点 是用边e连接的,e的两个端点是顶点 。
注释1.1若在图G中删除边e后,图G的分支数增加,则称边e为图G的割边。
注释1.2若边e的两个端点是相同的顶点,则e为环边。
注释1.3若连接同一对顶点的边数大于1,则这样的边称为多重边。
2.2. 连通图
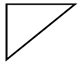
定义1.4若从顶点V1到顶点V2有路径,则称顶点V1与顶点V2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。即图中任意两顶点间至少有一条路径。如图1左图为连通图,右图为非连通图。(注:本文涉及的图均为连通平面图。)
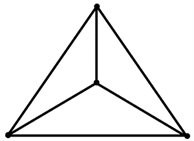
Figure 1. Connected graph and unconnected graph
图1. 连通图与非连通图
2.3. Tutte多项式
性质1:当图G的边集是空集时, ;
性质2:当e是环边时, ;
性质3:当e是割边时, ;
性质4:当e不是环边也不是割边时, 。
3. 图的Tutte多项式
3.1. 图的Tutte多项式的计算
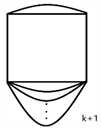
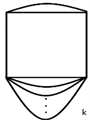
定义2.1在四边形的基础上,任意选择一组对边,分别增加m条边和n条边,得到的图称为 图(如图2)。
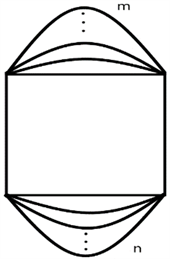
Figure 2. Graph
图2. 图
定理2.1图G 的Tutte多项式为:
证明:当 ,
时,
(  )
(
)
(  )
( )
)
( )
(  )
(
)
(  )
( )
)
( )
(  )
(
)
(  )
( )
)
( )
(  )
)
假设 时, ,
下证
成立,
(  )
(
)
(  )
( )
)
( )
则 成立。
与 同理,利用Tutte多项式减边缩边性质可以证得:
.
设 ;
,
下证 成立,
(  )
(
)
(  )
( )
)
( )
( )
其中,
( 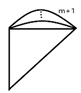 )
(
)
(  ) +
( )
) +
( )
则
定理2.1得证。
3.2. 图的Tutte多项式的计算
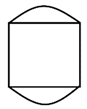
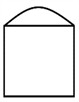
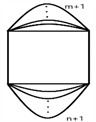
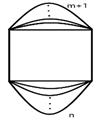
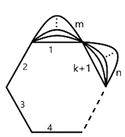
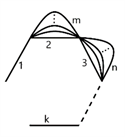
定义5.1在A边形( )的基础上,任选两邻边,分别为其增加m条边和n条边,得到的图称为 图(如图3)。

Figure 3. Graph
图3. 图
定理5.1 图的Tutte多项式为:
证明:当 时,与 图的Tutte多项式一样,借助二变量的数学归纳法即可证明成立。
设 成立,即 ,
下证 成立。
(  )
(
)
(  )
)
(  )
(
)
( 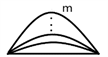 )
)
其中,
( 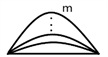 )
(
)
(  )
( )
)
( )
(  )
( )
)
( )
则
定理5.1得证。
4. 结论
本文主要研究了一类 ( )图的Tutte多项式,目前学者们只得到轮图、扇图与花图Tutte多项式的具体表达,未来会得到更多图的Tutte多项式,也可以进一步分析得到图的很多信息与参数。
文章引用
祁 禄. 一类连通图的Tutte多项式
The Tutte Polinomials of a Kind of Connected Graphs[J]. 应用数学进展, 2023, 12(02): 728-733. https://doi.org/10.12677/AAM.2023.122074
参考文献
- 1. Brylawski, T. and Oxley, J. (1992) The Tutte Polynomial and Its Applications. Matroid Applications, 40, 123-155. https://doi.org/10.1017/CBO9780511662041.007
- 2. Jin, X. and Zhang, Z. (2010) Zeros of the Jones Polynomial Are Dense in the Complex Plane. The Electronic Journal of Combinatorics, 17, 2493-2503. https://doi.org/10.37236/366
- 3. Jaeger, F. (1988) Tutte Polynomials and Link Polynomials. Proceedings of the American Mathematical Society, 103, 647-654. https://doi.org/10.1090/S0002-9939-1988-0943099-0
- 4. Doslic, T. (2013) Planar Polycyclic Graphs and Their Tutte Polynomials. Journal of Mathematical Chemistry, 51, 1599-1607. https://doi.org/10.1007/s10910-013-0167-2
- 5. Brennan, C., Mphako, E. and Mansour, T. (2014) Tutte Polyno-mials of Wheels via Generating Functions. Bulletin of the Iranian Mathematical Society, 39, 881-891.
- 6. 廖云华. 图多项式若干问题研究[D]: [博士学位论文]. 长沙: 湖南师范大学, 2015.
- 7. Kung, J.P.S. (2008) Old and New Perspectives on the Tutte Polynomial. Annals of Combinatorics, 12, 133-137. https://doi.org/10.1007/s00026-008-0342-5