Advances in Applied Mathematics
Vol.06 No.04(2017), Article ID:21533,7
pages
10.12677/AAM.2017.64075
Numerical Algorithm for a Class of Fredholm Integro-Differential Boundary Value Problems
Yongfang Zhou1, Lihua Mu2, Jinghe Li1, Lijun Ma1
1School of Science, Hebei University of Technology, Tianjin
2School of Science, Heilongjiang University of Science and Technology, Harbin Heilongjiang

Received: Jul. 8th, 2017; accepted: Jul. 24th, 2017; published: Jul. 27th, 2017

ABSTRACT
This paper discusses the numerical method for a class of Fredholm integro-differential boundary value problems. By constructing the reproducing kernel space which satisfies the boundary conditions, the simple reproducing kernel numerical approximate method is established. The paper describes both the exact solution obtained in the form of series and the approximate solution obtained by truncating the series representation of the exact solution. Error estimation of the method was discussed. The results of numerical simulation demonstrate the validity of the method in the paper.
Keywords:Boundary Value Problems, Integro-Differential Equation, Reproducing Kernel Space
一类Fredholm积分微分方程边值问题的 数值方法
周永芳1,母丽华2,李景和1,马丽君1
1河北工业大学理学院,天津
2黑龙江科技大学理学院,黑龙江 哈尔滨
收稿日期:2017年7月8日;录用日期:2017年7月24日;发布日期:2017年7月27日

摘 要
本文讨论Fredholm积分微分方程边值问题的数值方法。通过建立满足边界条件的再生核空间,获得简单易行的再生核数值逼近方法。给出方程精确解的级数表达式,通过截断级数获得方程的近似解,并给出了误差估计。数值模拟结果说明本文方法的有效性。
关键词 :边值问题,积分微分方程,再生核空间

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Fredholm积分微分方程边值问题广泛地出现在力学、物理学、化学、天文学、生物学、经济学以及静电学 [1] 等科学和工程问题 [2] 之中。这类问题解的存在性与唯一性研究可以参见文献 [3] 。许多学者致力于方程(1)的数值方法研究,这些方法包括Adomian分解法、变分迭代法、同伦分析法、小波法、凸方法、泰勒级数展开法 [4] [5] [6] 等。这些方法各有优缺点,不断地寻找更加有效,简单的数值方法是学者们一直关心的热点问题。
近年来,再生核数值方法广泛地应用于微分方程边值问题的数值求解 [7] [8] [9] [10] [11] ,本文将建立包含边界条件的再生核空间,在空间中讨论如下Fredholm积分微分方程边值问题
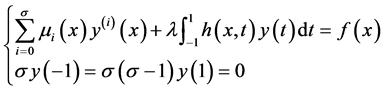 (1)
(1)
精确解的表达形式,通过截断级数给出方程的近似解,证明了近似解一致收敛于方程精确解。其中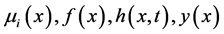 是
是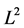 空间上的连续函数,
空间上的连续函数,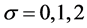 ,
,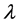 是一个参数。
是一个参数。
2. 再生核空间
定义1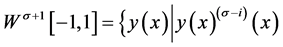 是绝对连续实值函数,
是绝对连续实值函数, 是整数,
是整数,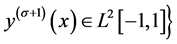 。
。
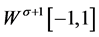 是再生核空间(证明参见文献 [12] ),对任意的
是再生核空间(证明参见文献 [12] ),对任意的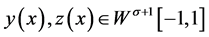 ,内积和范数分别为
,内积和范数分别为
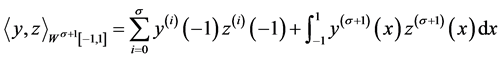 ,
,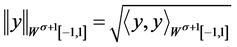 .
.
定义2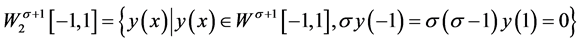 。
。
 是
是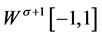 的闭子空间(证明参见文献 [12] ),
的闭子空间(证明参见文献 [12] ),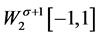 是再生核空间。
是再生核空间。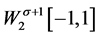 的再生核函数为
的再生核函数为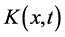 (具体表达式的确定参见文献 [12] )。
(具体表达式的确定参见文献 [12] )。
定义3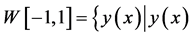 是绝对连续实值函数,
是绝对连续实值函数, 。
。
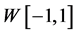 是再生核空间,对任意的
是再生核空间,对任意的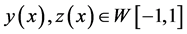 ,内积和范数分别为
,内积和范数分别为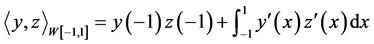 ,
,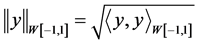 。设
。设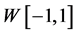 的再生核函数为
的再生核函数为 (具体表达式的确定参见文献 [12] )。
(具体表达式的确定参见文献 [12] )。
3. 精确解和近似解的构造
定义线性算子 :
: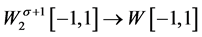 。对任意
。对任意 ,
,
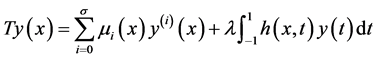 ,
,
则方程(1)转化成如下形式:
 , (2)
, (2)
其中,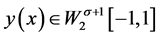 ,当
,当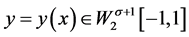 时,
时,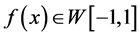 。
。
引理1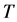 :
: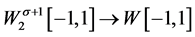 是有界线性算子。
是有界线性算子。
设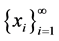 是
是 上的稠密子集。
上的稠密子集。
令 ,其中,
,其中,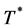 是
是 的共轭算子。
的共轭算子。
引理2假设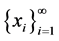 在
在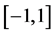 上稠密,则
上稠密,则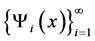 是
是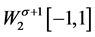 上的完全系。
上的完全系。
证明 注意到
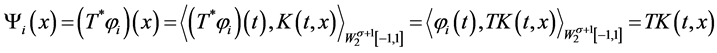
显然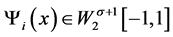 。令
。令
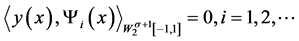 ,
,
其中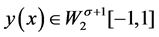 ,即得
,即得
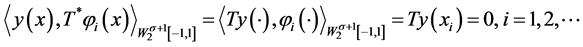 .
.
由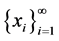 在
在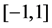 上稠密,故
上稠密,故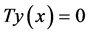 。由
。由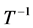 的存在性可知
的存在性可知 ,定理得证。
,定理得证。
我们将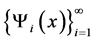 Gram-Schmidt正交化,得到
Gram-Schmidt正交化,得到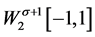 上的完全正交系
上的完全正交系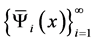 ,这里
,这里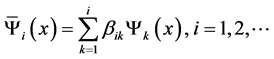 ,其中,
,其中,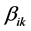 是正交化系数。
是正交化系数。
定理1假设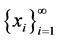 在
在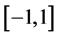 上稠密,如果
上稠密,如果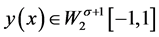 是方程(2)的解,则
是方程(2)的解,则
 , (3)
, (3)
其中,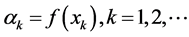 。
。
证明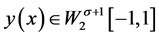 ,
,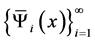 是
是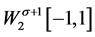 上的完全正交系,于是
上的完全正交系,于是
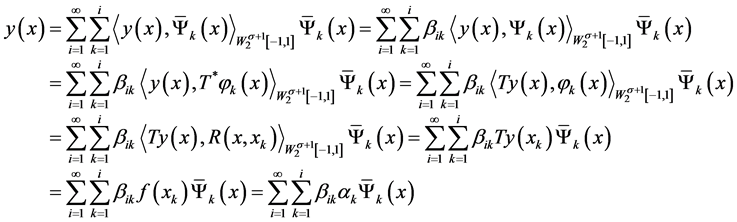
定理1给出了方程(2)精确解的表达式。
通过截断式(3)中给定的级数,得到方程(2)的近似解
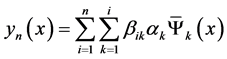 , (4)
, (4)
显然,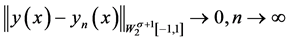 。
。
定理 2 假设方程(2)的解存在唯一,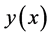 是方程(2)的解,
是方程(2)的解, 是方程的近似解由式(4)给出,则
是方程的近似解由式(4)给出,则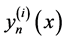 是一致收敛的,其中
是一致收敛的,其中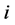 依次取
依次取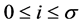 的所有正整数,即
的所有正整数,即
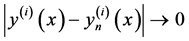 ,
,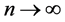 .
.
证明 注意到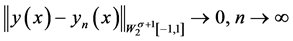 ,于是当
,于是当 时,有
时,有
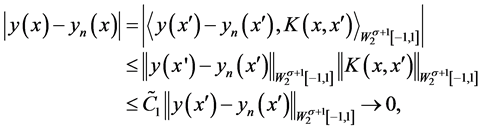
类似的
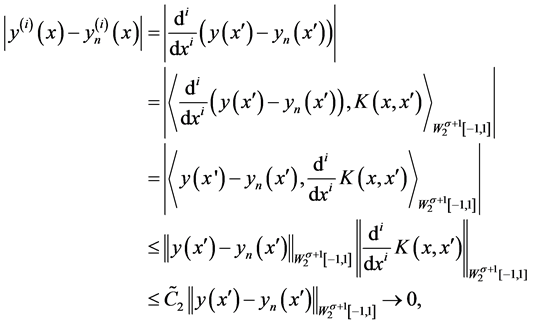
这里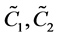 是常数。
是常数。
4. 误差估计
对于正整数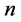 , 在区间
, 在区间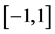 上,记
上,记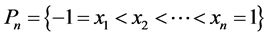 ,
,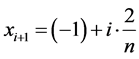 ,
,
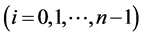 ,令
,令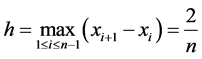 。
。
定理 3 设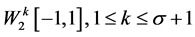 是再生核空间,方程(1)的精确解
是再生核空间,方程(1)的精确解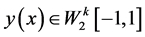 ,
,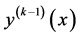 是Lipschitz连续的,
是Lipschitz连续的,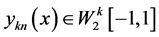 是方程(1)的近似解,且
是方程(1)的近似解,且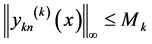 ,则
,则
 (5)
(5)
其中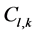 ,
,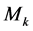 是常数。
是常数。
证明 利用数学归纳法证明。
首先,对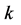 采用数学归纳法。
采用数学归纳法。
假设结论对于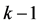 时成立,我们来证明对于
时成立,我们来证明对于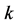 成立。
成立。
设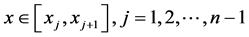 ,有
,有
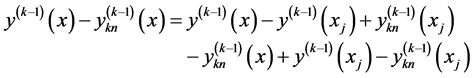 (6)
(6)
由于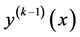 是Lipschitz连续的,所以存在
是Lipschitz连续的,所以存在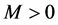 ,使得
,使得
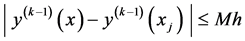 (7)
(7)
因为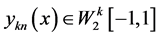 ,有
,有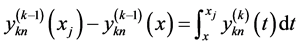
因此
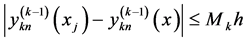 (8)
(8)
给定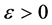 ,由定理2可知,当
,由定理2可知,当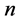 充分大时,有
充分大时,有
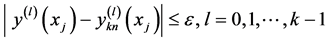 (9)
(9)
由(6)~(9),得
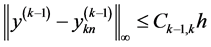 (10)
(10)
其次,对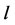 采用数学归纳法,当
采用数学归纳法,当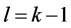 时,有(5)和(10)成立。
时,有(5)和(10)成立。
假设当 成立,即
成立,即
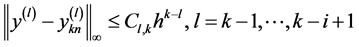 (11)
(11)
接下来,我们证明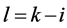 的情况。
的情况。
因为 ,所以有
,所以有
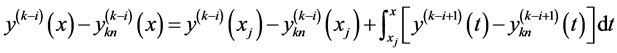 (12)
(12)
由(9)~(12),我们有
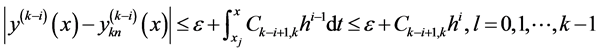
则有
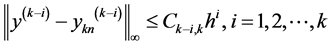
定理得证。
Table 1. Numerical results of example 1
表1. 算例1的数值结果
5. 数值算例
算例1 求解下列Fredholm积分微分方程边值问题

精确解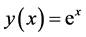 ,取
,取 ,数值结果见表1。在表1中给出了算例1中方程近似解的计算结果和误差。
,数值结果见表1。在表1中给出了算例1中方程近似解的计算结果和误差。
6. 结论
文中通过构造包含方程边值条件的再生核空间,获得了一类Fredholm积分微分方程边值问题的精确解和近似解,证明了方程近似解及其导数的一致收敛性,给出了数值方法的误差估计。实验结果表明该方法是有效的。该方法可以进一步推广到其他线性方程边值问题的求解中。
基金项目
河北省自然科学基金(A2015202335),黑龙江省自然科学基金(A201421)。
文章引用
周永芳,母丽华,李景和,马丽君. 一类Fredholm积分微分方程边值问题的数值方法
Numerical Algorithm for a Class of Fredholm Integro-Differential Boundary Value Problems[J]. 应用数学进展, 2017, 06(04): 644-650. http://dx.doi.org/10.12677/AAM.2017.64075
参考文献 (References)
- 1. Jaradat, H., Alsayyed, O., and Al-Shara, S. (2008) Numerical Solution of Linear Integro-Differential Equations. Journal of Mathe-matics and Statistics, 4, 250-254. https://doi.org/10.3844/jmssp.2008.250.254
- 2. Saadatmandia, A. and Dehghan, M. (2010) Numerical Solution of the Higher-Order Linear Fredholm Integro Diffrential-Difference Equation with Variable Coefficients. Applied Mathematics and Computation, 59, 2996-3004. https://doi.org/10.1016/j.camwa.2010.02.018
- 3. Agarwal, R. (1986) Boundary Value Problems for High Order Differential Equations. World Scientific, Singapore.
- 4. Bildik, N., Konuralp, A. and Yalçinbas S. (2010) Comparison of Legendre Polynomial Approximation and Variational Iteration Method for the Solutions of General Linear Fredholm Integro-Differential Equations. Applied Mathematics and Computation, 59, 1909-1917. https://doi.org/10.1016/j.camwa.2009.06.022
- 5. Hashim, I. (2006) Adomian Decomposition Method for Solving BVPs for Fourth-Order Integro-Differential Equations. Journal of Computational and Applied Mathematics, 193, 658-664. https://doi.org/10.1016/j.cam.2005.05.034
- 6. Hosseini, S. and Shahmorad, S. (2003) Tau Numerical Solution of Fredholm Integro-Differential Equations with Arbitrary Polynomial Bases. Applied Mathematical Modelling, 27, 145-154. https://doi.org/10.1016/S0307-904X(02)00099-9
- 7. Li, X.Y. and Wu, B.Y. (2015) Approximate Analytical Solutions of Nonlocal Fractional Boundary Value Problems. Applied Mathematical Modelling, 39, 1717-1724. https://doi.org/10.1016/j.apm.2014.09.035
- 8. Geng, F.Z. and Qian, S.P. (2014) A New Reproducing Kernel Method for Linear Nonlocal Boundary Value Problems. Applied Mathematics and Computation, 248, 421-425. https://doi.org/10.1016/j.amc.2014.10.002
- 9. Wu, B.Y., Guo, L.H. and Zhang, D.Z. (2015) A Novel Method for Solving a Class of Second Order Nonlinear Differential Equations with Finitely Many Singularities. Applied Mathematics Letters, 41, 1-6.
- 10. Wu, B.Y. and Li, X.Y. (2010) Application of Reproducing Kernel Method to Third Order Three-point Boundary Value Problems. Applied Mathematics and Computation, 217, 3425-3428. https://doi.org/10.1016/j.amc.2010.09.009
- 11. Zhou, Y.F., Cui, M.G. and Lin, Y.Z. (2010) A Computational Method for Nonlinear 2m-th Order Boundary Value Problems. Mathematical Mod-elling and Analysis, 15, 571-586. https://doi.org/10.3846/1392-6292.2010.15.571-586
- 12. 周永芳. 若干微分方程非局部边值问题的一种数值方法[D]: [博士学位论文]. 哈尔滨: 哈尔滨工业大学, 2011.
