Advances in Applied Mathematics
Vol.
11
No.
09
(
2022
), Article ID:
55738
,
11
pages
10.12677/AAM.2022.119670
求解随机常微分方程的深度学习法
孙保龙,杨明智,李强,晏洋天,魏云鹏
河南科技大学数学与统计学院,河南 洛阳
收稿日期:2022年8月9日;录用日期:2022年9月2日;发布日期:2022年9月14日

摘要
随机微分方程是在确定性微分方程中加入非确定性的随机项从而产生的新方程。它在描述客观现象中起着举足轻重的作用。因此,研究随机微分方程解的形式和性态显得尤为重要。然而,一般情况下,随机微分方程的解析解无法求出。因此,寻找随机微分方程的数值解就显得尤为重要。本文在欧拉法的思想上,成功构造了深度学习训练的样本集,并采用每一轮预测的斜率与初始条件实现了损失函数的构造,成功将深度学习方法应用于求解常微分方程,并获得了优于欧拉法精度的深度学习结果;在此基础上,使用小区间样本集斜率的平均值代替欧拉法中小区间初始点斜率,结合米尔斯坦法的思想,构造出了深度学习方法的迭代格式,并成功将其应用于求解一个具体的随机微分方程(Black-Scholes方程)。数值结果表明:所构造的深度学习方法比常规的欧拉法和米尔斯坦法精度更高。
关键词
随机微分方程,深度学习法,米尔斯坦法,欧拉法

Deep Learning Method for Solving Stochastic Ordinary Differential Equations
Baolong Sun, Mingzhi Yang, Qiang Li, Yangtian Yan, Yunpeng Wei
School of Mathematics and Statistics, Henan University of Science and Technology, Luoyang Henan
Received: Aug. 9th, 2022; accepted: Sep. 2nd, 2022; published: Sep. 14th, 2022

ABSTRACT
Stochastic differential equations are new equations that arise by adding non-deterministic stochastic terms to deterministic differential equations. It plays a pivotal role in describing objective phenomena. Therefore, it is particularly important to study the form and properties of the solutions of stochastic differential equations. However, in general, the analytical solutions of stochastic differential equations cannot be found. Therefore, it is particularly important to find the numerical solutions of stochastic differential equations. In this paper, based on the idea of Euler’s method, the sample set for deep learning training is successfully constructed, and the slope of each round of prediction with the initial condition is used to realize the construction of loss function, and the deep learning method is successfully applied to solve the ordinary differential equation, and the deep learning results with better accuracy than Euler’s method are obtained; on this basis, the average of the slope of small interval sample set is used instead of the slope of the initial point of small interval of Euler’s method, and the combination of based on this, the iterative format of the deep learning method is constructed using the average of the small interval sample set instead of the initial slope of the small interval of the Euler method, and combined with the idea of Milstein method, and successfully applied to solve a specific stochastic differential equation (Black- Scholes equation). Numerical results show that the constructed deep learning method is more accurate than the conventional Euler’s and Milstein’s methods.
Keywords:Stochastic Differential Equations, Deep Learning Method, Milstein Method, Euler Method

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着社会的不断发展,人们对于现实世界的描述逐渐从语言转变向理论方面,这其中微分方程有深刻而生动的实际背景。它从生产实践和科学技术中发展而来,是用来描述现实世界的一个强有力的工具。在人们探究物质世界运动规律时,一般很难以探究出物质原本的运动规律,这是因为现实世界是一个极其复杂的概念,外界的一点变动对于物质运动规律都将产生影响。因此我们用微分方程来刻画它们的关系,对应的运动规律可以用微分方程的解来描述。而在研究实际数学模型过程中,由于外界存在不确定因素,所以总体上很复杂,研究数学模型就会有不确定性的因素,而在经济学、金融学、保险学、人口增长理论、信号处理等领域,不确定因素是不能忽视的。在1944年,伊藤清定义了与Wiener过程 [1] 相应的随机系统的伊藤积分,由此便有了描述了各种物理现象的微分方程即随机微分方程。但是一般很难给出随机微分方程的解析解。因此我们迫切需要构造数值解来近似解析解并且要保证数值解一定的精度与稳定性。得益于计算机计算能力的飞速提高以及深度学习良好的实际应用,数值求解和模拟随机微分方程的精度在不断地扩大和提高,这对于我们用已知把握未知具有极其重要的现实意义。
国内外论文研究
目前随机微分方程的数值求解方法有欧拉法 [2]。它是一种解决数值常微分方程的最基本的一类显型方法。龙格库塔法 [3] 的主要思路是设法多预测几个点的斜率并进行加权求和,加权系数通过泰勒展开使得误差尽可能提高来确定。这两种方法都是只选用单步长(1个点)来预测,为此阿达姆斯法 [4] 选用线性多步长的方法提高了预测的准确性。以上都是经典的微分方程数值解方法。此外,随机微分方程求解的数值方法还依赖于相应偏微分方程解的合适概率表示的随机近似方法,例如基于倒向随机微分方程 [5] 的概率表示,基于二阶倒向随机微分方程 [6] 的概率表示以及基于经典Feynman-Kac公式 [7] 扩展的概率表示等。物理知识深度学习模型 [8] 也可以用于随机微分方程求解,通过将数据观测与PDE模型合并起来去估计深度神经网络模型。它的基本原理是利用物理动力学应遵循一类偏微分方程的先验知识,从有限数据去估计物理模型,从而使用深度神经网络在一个和两个空间维度上解决偏微分方程。深度神经网络 [9] 已成功用于模拟雷诺平均Navier-Stokes (RANS)模型中的雷诺应力。此外,卷积神经网络可用来求解大型稀疏线性系统 [10] ,并成功用于求解Navier-Stokes偏微分方程数值解。
2. 预备知识
2.1. 布朗运动
考虑概率空间 ,在这个概率空间上满足下列条件实值随机过程 ,就把 称之为标准布朗运动。
1) 样本函数 是连续的,对于几乎全部的 同时
2) 对所有的符合条件 的实数 有 独立于过去的状态
3) 当 时, 服从正态分布 ,且该正态分布均值为0,方差为
若对于非标准的布朗运动,我们可以通过线性变换的方法把非标准布朗运动变为标准布朗运动。故在本文中考虑的布朗运动均为标准布朗运动。
2.2. 伊藤随机微分方程 及解的定义
下面展开对随机微分方程的介绍。凡确定地依赖于初始状态的时间系统,通常可以用Ordinary Differential Equation (ODE)来表示,具体形式如下。
(2.1)
然而实际生活中,对于一般常微分方程,由于自然界往往会存在一些细微变动,这些随机干扰使得时间系统表现出不确定性,这就产生了一些随机部分,我们称之为随机干扰项。将之转化为随机微分方程Stochastic Differential Equation (SDE)。
(2.2)
其中 ,自治的随机微分方程的形式如下。
(2.3)
若随机过程 满足如下条件。
1) 为连续适应过程
2)
3) 满足随机微分方程(2.2)
那么就称 为方程(2.2)满足初值为 的解。
2.3. 深度学习方法
2.3.1. 神经元模型
在介绍深度学习之前我们先引入神经网络中单个神经元的具体工作原理,这是通过对于人脑神经元的模拟得出的一种数学模型。这里引入的是具有4个神经元输入的神经元 [11] ,如图1所示。
图中 表示的是4个神经元输入,是具体的数值, 为其对应的权重,K阈值是模仿一个单位元的刺激上限,对应这个神经元的输出为 ,其中 为激活函数。一些常见的激活函数有Sigmoid函数,双曲正切函数,SoftPlus函数和ReLU函数 [12]。在本文中选取的是双曲正切激活函数,其表达式如下所示。
(2.4)
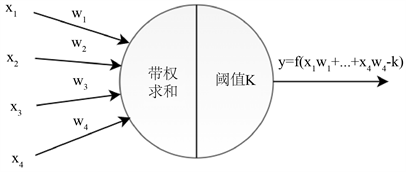
Figure 1. Single neuron model
图1. 单个神经元模型
2.3.2. 正向传播
考虑到神经元之间的关系可能会很复杂,往往不是简单的一对一的神经元传送,可能会出现诸如层次的关系。我们把最初输入的层称为输入层,输出结果的层叫做输出层,中间的神经元组成的层叫做隐藏层,隐藏层的层数可能很高。现只给出隐藏层是1层时的具体情况,如图2所示。
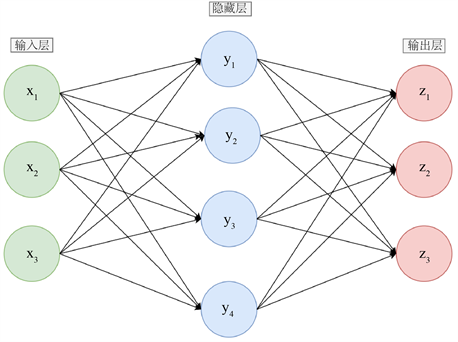
Figure 2. Single hidden layer model
图2. 单隐藏层模型
上图中代表正向传播神经网络,每个神经元的工作状态如图1所示。一般深度学习的隐藏层的层数为5层,6层甚至高达10多层。
2.3.3. 反向传播调参
对于给定输入层,输出层,隐藏层,未知参数是每个神经元的阈值以及相互连接的权重,我们定义损失函数,对于输入值进行正向传播,并且根据损失函数的结果判断,若不满足精度要求,进行反向传播,更新每个神经元的参数,如此往复直到达到精度要求。
2.4. 深度学习求解显式常微分方程
对于满足初值条件 的常微分方程 ,下面是一些具体深度学习算法的属性设置,本文中深度学习选用的框架是torch1.11.0,运行环境为 python3.7.1。
首先生成训练样本点。考虑区间 ,给定一个预备值N,对区间进行N等分,记作 。目的是拟合 ,使得所连接的曲线尽可能符合解析解。
接着设置损失函数。对于深度学习损失函数,主要考虑初值条件以及微分近似方面 [13]。首先对小区间进行M等分,产生了横坐标点序列 。对于微分近似,使用torch自带的求微分模块
torch.autograd.grad可以对第k轮产生的数组 进行求微分运算并且与具体的微分值 进
行比较。对于初值条件,考虑误差 为与 的差别。第k轮损失函数如下所示。
(2.5)
上式中的 并不是说明拟合的积分曲线在区间内可微甚至在一点处可微,而仅仅是调用微分模块torch.autograd.grad进行该点近似微分值大小的估计。
最后设置隐藏层参数。一般而言隐藏层层数越多,每层里面的神经元越多,结果拟合的就越好。但是这往往会造成算力的浪费并且可能会产生过拟合现象,即模型在训练集上表现不错但是在测试集上表现一般,而层数或者神经元过少起不到泛化作用,为此使用神经网络中的经验公式 [14] 进行初始层数确定。
(2.6)
其中,n为初始隐藏层数, 为输入神经元的数目, 为输出神经元的数目。
对于满足初值条件 的常微分方程 ,主要区别在于损失函数的构造。由于每一轮真实值的微分与 有关(其中 表示在 处真实的值),但是在预先 不知时真实微分难以计算出来。为此我们近似用 来表示精确值微分,第k轮损失函数如下所示。
(2.7)
具体的一个神经网络的架构如图3所示。
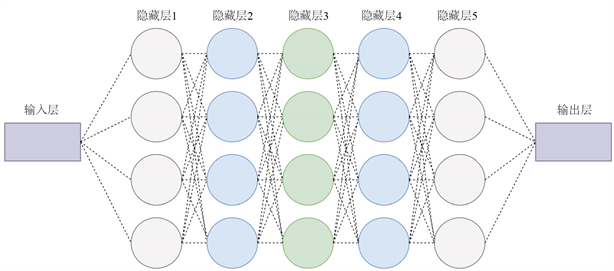
Figure 3. The structure of neural network
图3. 神经网络结构图
上图中的神经网络结构是输入层、输出层以及5层隐藏层,其中每层隐藏层具有的神经元个数为5个,激活函数为双曲正切函数。网络结构的主要变化是隐藏层层数以及每个隐藏层神经元的个数。对于给定微分方程,使用式(2.7)作为损失函数,首先正向传递小区间的斜率值以及初值条件,经过神经元线性求和以及其非线性激活函数映射,最终输出到输出层,若精度不能达到要求,则反向传播调节各个神经元的阈值以及权重参数,反复迭代使得初值条件以及斜率误差达到所需精度要求。下面对常微分方程 进行数值解法。选用 ,进行不同网络架构( )的数值解(其中a代表隐藏层个数,b表示每层神经元个数)。每层神经元个数对于数值解的影响如图4所示。

Figure 4. Numerical solution for different number of neurons
图4. 不同神经元个数数值解图
上图中迭代次数是指当前小区间的位置,具体的误差是数值解与解析解的误差(平均绝对误差),当隐藏层层数固定时,随着每层神经元个数的增加数值解拟合效果提高,但是神经元个数过多时会使数值解拟合效果降低。隐藏层层数对于数值解的影响如图5所示。
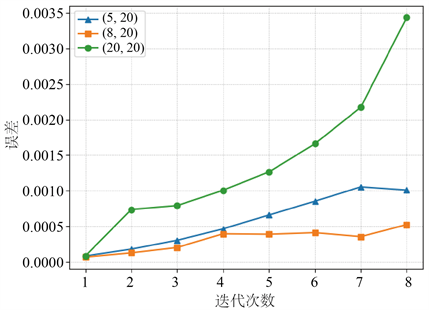
Figure 5. Numerical solution for different hidden layers
图5. 不同隐藏层层数数值解图
上图说明当每层神经元个数固定时,随着隐藏层层数的增加数值解拟合效果提高,但是隐藏层层数过多时会使数值解拟合效果降低。深度学习主要改变一个区间里欧拉法中的平均斜率。对于上述数值解的方程,分别选用当前区间下整个小区间斜率、前一半小区间斜率、第一个点斜率进行深度学习方法数值解以及欧拉法进行数值解,具体误差如图6所示。

Figure 6. Error comparison of numerical solutions of ordinary differential equations
图6. 常微分方程数值解误差对比
由上图可以看出,深度学习的精度比欧拉法高一个量级,并且平均斜率取值点越多深度学习方法拟合的精度就越高。
3. 随机常微分方程数值解
对于上文定义的伊藤随机微分方程,下面主要考虑其自治形式(2.3),并给出经典方法以及深度学习方法数值解的迭代格式。下面给出 的数值求解方法。
考虑在闭区间 上,对于给定的某个正整数N,步长 , 在
处的值为 ,并记 。则下面列出三种迭代格式。
欧拉法主要思想是使用一个点来代替一段小区间的平均斜率,其中显式欧拉法迭代格式如下所示。
(3.1)
米尔斯坦法在欧拉法的基础上加入了修正项,提高了其数值解拟合的精度,令 ,其具体的迭代格式如下所示。
(3.2)
本文所构造的深度学习方法在米尔斯坦方法的基础之上进行改善,实际上是对于(3.2)式中的 项进行改善。米尔斯坦方法均仅用到了 作为小区间的平均斜率,实际上这会产生一些误差,为此设计深度全连接网络来预测小区间上的平均斜率 ,得到迭代格式如下所示。
(3.3)
具体求解随机微分方程的步骤如图7所示。
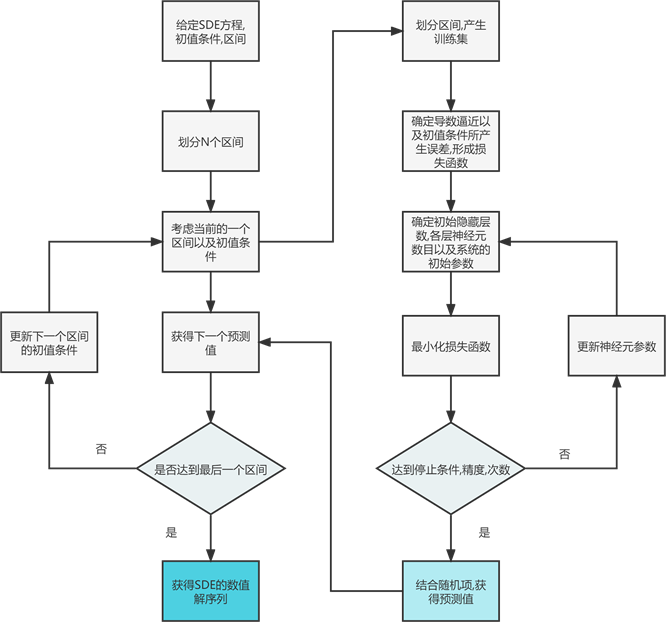
Figure 7. Deep learning flowchart for stochastic ordinary differential equations
图7. 随机常微分方程的深度学习流程图
4. 数值实验
下面将使用欧拉法、米尔斯坦法和深度学习方法对具有代表意义的随机常微分方程(Black-Scholes方程)进行数值解。其具体表达式如下所示。
(4.1)
其中 为常数,令 ,由伊藤公式 [15] 可求出Black-Scholes方程的解析解为
(4.2)
在上述自治随机常微分方程(4.1),令 ,可以得到随机常微分方程 。通过公式(4.2)可以计算出解析解为 。选定区间 ,固定N,解析解序列生成步骤如下。
1) 生成标准布朗运动 以及时间序列
2)
3) 遍历 ,获得解析解序列
接着使用欧拉法,米尔斯坦法,深度学习法进行求解,选用 ,具体数值解结果如图8所示。
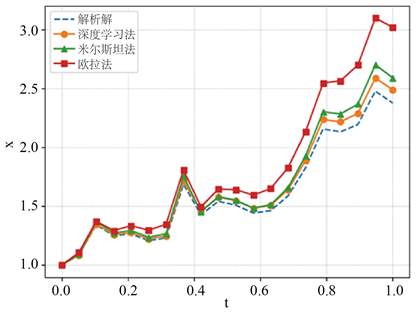
Figure 8. Simulation results of three methods and analytical solutions
图8. 三种方法与解析解的模拟结果图
上图表明 时,深度学习方法的精度最好,下面选用不同的N,各种方法的误差如表1~4所示。
Table 1. When N = 40, the error data of the three methods
表1. N = 40时,三种方法的误差数据
Table 2. When N = 80, the error data of the three methods
表2. N = 80时,三种方法的误差数据
Table 3. When N = 100, the error data of the three methods
表3. N = 100时,三种方法的误差数据
Table 4. When N = 300, the error data of the three methods
表4. N = 300时,三种方法的误差数据
5. 结论
本文采用深度学习法数值求解了随机微分方程。首先使用深度学习法求解了常微分方程:借用欧拉法思想,将区间等距离划分并对划分出的小区间继续等距离划分成深度学习训练的样本集,选用每一轮的预测出的斜率和初值条件进行损失函数的构造,结果表明深度学习方法在求解常微分方程时精度明显高于常规欧拉法;接着使用深度学习方法求解了一种随机微分方程(Black-Scholes方程):使用小区间样本集斜率的平均值来代替欧拉法中小区间初始点斜率,结合米尔斯坦法,构造出了深度学习方法的迭代格式,结果表明深度学习方法与米尔斯坦方法相比精度提高了50%。
本文构造了一种有效的求解随机Black-Scholes方程的深度学习法,该方法也有望推广到求解更复杂的随机微分方程中。
基金项目
河南科技大学大学生研究训练计划(SRTP)项目(项目编号:2021172)。
文章引用
孙保龙,杨明智,李 强,晏洋天,魏云鹏. 求解随机常微分方程的深度学习法
Deep Learning Method for Solving Stochastic Ordinary Differential Equations[J]. 应用数学进展, 2022, 11(09): 6342-6352. https://doi.org/10.12677/AAM.2022.119670
参考文献
- 1. Kloeden, P.E. and Platen, E. (1992) Stochastic Differential Equations. In: Kloeden, P.E. and Platen, E., Eds., Numerical Solution of Stochastic Differential Equations, Springer, Berlin, 103-160. https://doi.org/10.1007/978-3-662-12616-5_4
- 2. Hutzenthaler, M., Jentzen, A. and Kloeden, P.E. (2011) Strong and Weak Divergence in Finite Time of Euler’s Method for Stochastic Differential Equations with Non-Globally Lip-schitz Continuous Coefficients. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 467, 1563-1576. https://doi.org/10.1098/rspa.2010.0348
- 3. Dormand, J.R. and Prince, P.J. (1980) A Family of Embedded Runge-Kutta Formulae. Journal of Computational and Applied Mathematics, 6, 19-26. https://doi.org/10.1016/0771-050X(80)90013-3
- 4. Efendiev, B.I. (2020) Cauchy Problem for an Ordinary Dif-ferential Equation with a Distributed-Order Differentiation Operator. Differential Equations, 56, 658-670. https://doi.org/10.1134/S0012266120050110
- 5. Bismut, J.M. (1973) Conjugate Convex Functions in Optimal Stochastic Control. Journal of Mathematical Analysis and Applications, 44, 384-404. https://doi.org/10.1016/0022-247X(73)90066-8
- 6. Henry-Labordere, P., Tan, X. and Touzi, N. (2014) A Nu-merical Algorithm for a Class of BSDEs via the Branching Process. Stochastic Processes and Their Applications, 124, 1112-1140. https://doi.org/10.1016/j.spa.2013.10.005
- 7. Weinan, E., Hutzenthaler, M., Jentzen, A., et al. (2017) Linear Scaling Algorithms for Solving High-Dimensional Nonlinear Parabolic Differential Equations. SAM Research Report.
- 8. Raissi, M., Perdikaris, P. and Karniadakis, G.E. (2017) Physics Informed Deep Learning (Part I): Da-ta-Driven Solutions of Nonlinear Partial Differential Equations.
- 9. Ling, J., Kurzawski, A. and Templeton, J. (2016) Reynolds Averaged Turbulence Modelling Using Deep Neural Networks with Embedded Invariance. Journal of Fluid Mechanics, 807, 155-166. https://doi.org/10.1017/jfm.2016.615
- 10. Tompson, J., Schlachter, K., Sprechmann, P., et al. (2017) Accelerating Eulerian Fluid Simulation with Convolutional Networks. International Conference on Machine Learning, Sydney, 6-11 August 2017, 3424-3433.
- 11. Jin, W., Li, Z.J., Wei, L.S., et al. (2000) The Improvements of BP Neural Network Learning Algorithm. 2000 5th International Conference on Signal Processing Proceedings, Vol. 3, 1647-1649.
- 12. Samek, W., Binder, A., Montavon, G., et al. (2016) Evaluating the Visualization of What a Deep Neu-ral Network Has Learned. IEEE Transactions on Neural Networks and Learning Systems, 28, 2660-2673. https://doi.org/10.1109/TNNLS.2016.2599820
- 13. Lagaris, I.E., Likas, A. and, D.I. (1998) Artificial Neural Net-works for Solving Ordinary and Partial Differential Equations. IEEE Transactions Fotiadis on Neural Networks, 9, 987-1000. https://doi.org/10.1109/72.712178
- 14. Li, J., Cheng, J., Shi, J., et al. (2012) Brief Introduction of Back Propagation (BP) Neural Network Algorithm and Its Improvement. In: Jin, D. and Lin, S., Eds., Advances in Computer Science and Information Engineering, Springer, Berlin, 553-558. https://doi.org/10.1007/978-3-642-30223-7_87
- 15. Evans, L.C. (2012) An Introduction to Stochastic Differential Equations. American Mathematical Society, Rhode Island. https://doi.org/10.1090/mbk/082
