 Advances in Porous Flow 渗流力学进展, 2012, 2, 29-34 http://dx.doi.org/10.12677/apf.2012.23005 Published Online September 2012 (http://www.hanspub.org/journal/apf.html) A New Model of Liquid Flows in Low Permeability Reservoirs* Fuquan Song1, Li Yu2 1Petrochemical College, Zhejiang Ocean University, Zhoushan 2Jiangsu Oil Field Branch Company, Sinopec. Corp., Yangzhou Email: fqsong2000@smmail.cn Received: Jun. 3rd, 2012; revised: Jun. 9th, 2012; accepted: Jun. 13th, 2012 Abstract: In the petroleum development engineering, the low permeability reservoir is that the permeability of porous media is lower than 50 micro-Darcy. Because of the existence of the threshold pressure gradient (TPG), the mathe mati- cal model of liquid flow in low permeability media is difficult to describe this kind of flow. Until now there is not an ideal model, although there are several models used to fields of well testing analysis and petroleum numerical simula- tions. Based on the force between liquid and surface solid, and the negative slip boundary model of a micro-channel, a new liquid flow model was derived for low permeability reservoirs in this paper. First defined the no movement liquid layer close to the solid surface as the boundary stick layer which regarded as the negative slip length, and used the in- verse proportion of the height of the boundary stick layer to the pressure drop gradient, the formulae of liquid velocity and the flow rate of a round channel were derived; Then the model of liquid flows in low permeability reservoirs was gotten based on the cap illaries model; Finally the flow models were tested by examples and shown how to get the TPG of a low permeability reservoir. The results show that the new model has a clear physical definition, and can be easily used to describe liquid flows in low permeability media. Keywords: Low Permeability Reservoirs; No-Darcy’s Law; Threshold Pressure Gradient; The Boundary Stick Layer 低渗透油藏渗流模型新解* 宋付权 1,俞 力2 1浙江海洋学院,石油化工学院,舟山 2中国石油化工股份有限公司江苏油田分公司,扬州 Email: fqsong2000@smmail.cn 收稿日期:2012 年6月3日;修回日期:2012 年6月9日;录用日期:2012 年6月13 日 摘 要:工程上将多孔介质的渗透率小于 50 毫达西的油藏,称为低渗透油藏。长期以来,由于存在启动压力, 低渗透油藏的渗流特征很难描述,至尽还没有理想的模型。本文考虑液体和固体壁面的相互吸引的性质,从微 管的负滑移边界模型出发,定义固壁边界附近不流动流体的流体层为边界黏附层,采用边界黏附层与压力梯度 成反比的实验经验公式,推导出了考虑边界负滑移条件下,圆管中的流速分布公式和流量公式。进而得到考虑 边界黏附层的低渗透渗流模型。最后以微管和低渗透岩心的流动实验对模型进行了验证,拟合出了相应的启动 压力梯度。分析表明:新的模型具有物理含义清晰,易于应用的特点,可广泛用于低渗透油藏的理论分析和开 发设计中。 关键词:低渗透油藏;非达西渗流;启动压力梯度;边界黏附层 *资助信息:本文得到国家自然科学基金:10972199,10932010 的资助。 Copyright © 2012 Hanspub 29  低渗透油藏渗流模型新解 1. 引言 工程上将多孔介质的渗透率小于 50 毫达西的油 藏,称为低渗透油藏。在低渗透油藏的开发中,由于 多孔介质的孔隙及喉道直径大部分小于 1微米,因此 流体和固壁的相互作用不可忽略,最典型的油藏生产 特征是:液体在低渗透油藏中渗流时存在启动压力梯 度(Threshold Pressure Gradient,简称 TPG,如图1所 示G点)[1-4]。启动压力梯度是指,当多孔介质中实际 的压力梯度下于某一阈值时,流体不动,只有当实际 压力梯度大于此阈值时,流体才能流动。 由于启动压力梯度是一个随外加压力梯度变化 的一个值,因此对于考虑启动压力梯度的渗流模型就 变得比较复杂:由于最小的启动压力梯度很难测量(很 难区分流动与不流动的界限),于是人们使用最广泛的 模型是拟启动压力模型[5,6],如图 1所示的 GS点:即 将大压力梯度下的流动-压力梯度曲线的直线段向前 延长,与压力轴的交点即定义为拟启动压力梯度 (Pseudo-Threshold Pressure Gradient,简称 PTPG),在 应用时,忽略小压力梯度下的曲线段,其渗流数学模 型为: 0, vKpG , S SS pG pG (1) 式中:v为渗流速度,m·s–1;K为渗透率,m2; 为 流体粘度,Pa.s;p为多孔介质中的压强,Pa;GS为 拟启动压力梯度,Pa·m–1。 除此之外还有分段渗流模型[7]和多参数渗流模型 [8]等模型,均是以实验数据为目标,用数学函数逼近 渗流曲线,准确性明显高于拟启动压力梯度模型,但 Figure 1. The sketch map of liquid flow through low perme ability porous media 图1. 低渗透油藏中液体渗流特征示意图 由于用于理论分析时,很难求出非定常渗流问题的解 析解,因此应用不如拟启动压力梯度模型广泛。 但拟启动压力梯度模型的缺点也很明显:即忽略 的小压力梯度下的渗流。因此无论是拟启动压力梯度 模型,还是分段模型和多参数模型,都不是理想的描 述低渗透油层渗流规律的公式。从 2000 年以后 10 年 的研究,关于低渗透油藏渗流的模型,没有什么大的 进展,2011 年有一篇关于低渗透非线性渗流模型的论 文[9],第一次给出了一个完整函数的模型,不但表面 非常完美,而且富含物理含义。此模型深深地引起了 我的兴趣,于是对其进行了深入的研究,发现该模型 的应用是需要条件的,并且在数学上是有缺陷的,本 文从此公式出发,首先指出该公式的缺陷,进而给出 更加严谨的低渗透渗流模型。 2. 原渗流模型的缺陷 在文[9]中,考虑启动压力和液体的屈服应力,并 进行近似后得到如下公式(文[9]中公式(6)) 2 111 12 1 463 1ccc cc K QA p pppc 20c (2) 式中:Q为渗流流量,m3·s–1;A为过流面积,m2;c1 为启动压力影响参数;c2为非牛顿流体影响参数。 这里我先用试算法来验证一下此公式,假定流体 为牛顿流体,即 ,则上式可以简化为, 2 11 1 46 1cc K QA p pppc –1 10.0001 MPamc (3) 假设 ,我们对大括号内的公 式 2 11 1 46 1cc pppc 进行试算,压力梯度从 0.000001~10 MPa/m,计算结果如表 1所示。 由公式(2)的物理含义可知,括号内的值应该是下 于1的正值,而计算结果出奇的乱,原因在于公式(6) 要有一个限制条件,即 1 pc,即在小的压力梯度 下公式(2)是错误的,因此文[9]得到的结论也只能在压 力较大的情况下使用,而不是一个所有压力下都适用 的公式。 下面我们再来分析产生这种错误的根源,在文[9] 的公式(4)中,假定边界层厚度与压力梯度的关系, Copyright © 2012 Hanspub 30  低渗透油藏渗流模型新解 Table 1. The resulting data of testing computations 表1. 压力梯度试算结果 压力梯度 (MPa.m-1) 2 11 1 46cc ppc 1p 0.000001 –6,061,005 0.00001 –666,706 0.0001 - 0.001 667 0.01 7.02 0.1 1.06 1 1.00 10 0.99997 100 0.99999 01 rcp (4) 式中,r0为孔隙半径,m; 为流体边界黏附层厚度, m。 这里没有考虑压力梯度的限制,即 1 pc 0 r ,从 而边界层厚度 。所以如果没有压力梯度 1 pc的限制,在低压下将出现边界层无限厚的错 误现象,而其厚度不能大于毛管的半径。并且从数学 上看:由于 0 01r ,所以 1 0cp,然而 c1 是常数,并不能保证所有的压力梯度都小于 c1。因此, 原文中公式(4),应该写为: 01 1 , rpc p c 01 , rc p (5) 但是,一旦这样有了限制条件,也就不存在文[9] 中形如公式(6)~(8)那么简单的式子了。总之一句话, 该文忽略了压力梯度较小的情况(公式(6)在推导中, 在小的压力梯度下,不存在高阶小项),因此该文得到 的公式是不正确的。特别是用到数值模拟中,有时会 出现莫名其妙的错误。至于为什么该公式可以描述低 渗透渗流,这是因为:它和以往其他模型的应用一样, 在大的压力梯度下是可以应用的。实质上该模型是一 个普通的两参数模型,并没有给出合理的在整个压力 梯度下的渗流解。 接下来,我们吸取文[9]的优点的基础上,进行正 确公式的推导。 3. 低渗透多孔介质渗流模型新解 首先我们讨论一下流体在管道中流动的边界模 型:在 18 世纪 Navier 就提出了流体固壁边界的速度 滑移模型。但在之后的几百年间,由于人类研究和利 用的空间都是宏观尺度的大空间,即尺度在毫米以上 的空间,滑移边界的影响微乎其微,因此滑移模型被 更传统无滑移边界模型(如图 2(a)所示)所代替。随着 近几十年来微纳米科技的发展,流体流动边界的速度 滑移变得不可忽略,滑移边界重新出现在人们的视野 中[10-19],如图 2(b)所示。 除了无滑移边界,对应于滑移边界,还有一种边 界:由于固液作用力强,在固壁附近的流体出现一定 厚度的不流动层,称为边界黏附层,这种边界模型称 为负滑移边界[20],如图 2(c)所示(b为负值,应该注意 的是:这里讲的负滑移并非是出现反向流动,而是速 度为零的流体边界,不是实际的固壁边界,因此此时 的流动模型,要分段表示,否则就会出现形如文[9] 的错误,应用时也会出现反常的流动)。如图 2所示, 为流体在管道中流动的三种边界模型:无滑移边界、 滑移边界和负滑移边界。 这里我们主要讨论负滑移边界流动模型,研究表 明:在流体和固壁润湿时,如水在亲水管道中流动, 流体流动时会出现边界不流动的黏附层,由于流体边 界黏附层的厚度多为微米级,或者小于微米级的,这 种现象在宏观尺度下表现不明显,而在微纳米尺度 下,对流动的影响很大。本文所研究的低渗透多孔介 质就是由于孔隙和通道集中于5微米以下,而出现负 滑移现象。下面我们对具有负滑移边界的微圆管中的 流体流动进行理论分析。 3.1. 考虑负滑移时牛顿流体在微圆管中的 速度及流量公式 根据牛顿流体的应力应变关系 (a) (b) (c) Figure 2. Models of boundary conditions of flow ((a) Model of no-slip; (b) Model of positive slippage; (c) Model of negative slippage) 图2. 流体固壁边界模型((a) 无滑移模型;(b) 正滑移模型;(c) 负 滑移模型) Copyright © 2012 Hanspub 31  低渗透油藏渗流模型新解 (6) 式中, 为流体所受的应力,Pa; 为流体的应变,s–1。 对于圆形的管道,方程(6)可以具体表达为, d 2d rv pr (7) 式中,r为圆管径向坐标,m。 假设边界黏附层的厚度为 ,滑移长度 b = – ,对 方程(7)从r到r0 + b进行积分, 0 dd 2 rr vpr 0 vr (8) 积分方程(8),得到了考虑负滑移时,流体在圆管 中的速度分布 22 4 rr vp 0 (9) 再对公式(9)进行过流断面上的积分,可以得到对 应的流量公式, 4 0 8 r Qp (10) 当边界黏附层厚度为零时,公式(10)退化为无滑 移边界模型的流量公式,即Hagen-Poisseuille 公式[17], 4 HP 128 dp QL HP L (11) 式中,Q为Hagen-Poisseuille 流量,m3·s–1,d为圆 管的直径,m; 为圆管的长度,m。 实验表明[9]:对于同一根毛管,压力梯度越大, 壁面粘滞层越薄,即 r 越小, r 与压力梯度成反 比关系,故可假设 01 1 , rpc p c 0 r 01 , rc p (12) 当 1 Gc 时,整个流体均不流动,此时的最大压力梯 度,称为启动压力梯度 G,由(12)式可知: , 这就是启动压力梯度的定义,即当外加压力梯度下于 启动压力梯度时,流体不流动。因此公式(12)有个更 有物理意义的公式形式, 0 0 , ,rGp 由公式(13)可以得到不同压力梯度下的黏附层厚 度,如图 3为不同启动压力梯度情况下的边界黏附层 厚度图(相当于负滑移长度):边界黏附层的厚度随压 力梯度的增大而增大,即在小压力梯度下,界面作用 力明显;而在大的外力作用下界面因素对流动的影响 很小。这里需要注意的是:边界黏附层的厚度是不能 大于微管半径的。 则圆管中的流速和流量公式分别为: rpG p G (13) 222 0 0, 1, 4 pG Gprr vppG (14) 4 4 0 0, 1, 8 pG QrGp ppG (15) 假设水在直径为 10 微米的微管中流动,粘度为 1 mPa. s ,由 公 式(14)可计算出不同压力梯度下的流速分 布。如图 4所示:在启动压力梯度较小时(Go = 0.01 MPa/m),流动特征接近于 H-P 流动的速度分布,当启 动压力梯度较大时,可以在固液边界附件看到明显的 速度为 0的黏附层。 由公式(15)可以计算出微管中的流量,如图 5为 对应的不同启动压力梯度影响的水在10 微米微管中 流动的流量图,可以看出:界面的影响主要在小压力 下,当压力梯度较大时,在不同的启动压力梯度下, 流动特征相同。 Figure 3. The height of adherent boundary fluid affected by TPG through a channel of 10 um d i ameter 图3. 10微米微管中启动压力梯度影响的黏附层厚度 Copyright © 2012 Hanspub 32 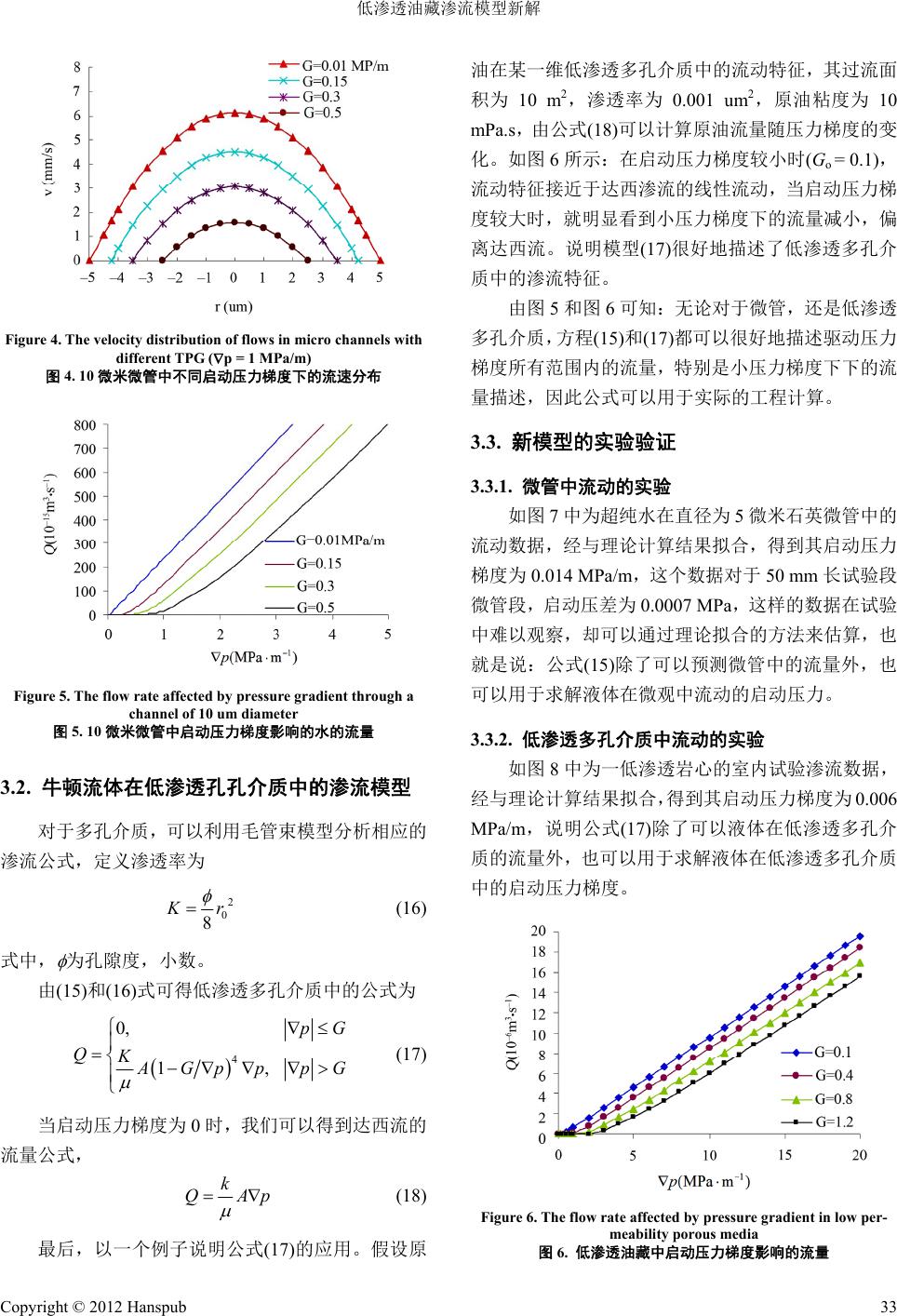 低渗透油藏渗流模型新解 Figure 4. The velocity distribution of flows in micro channels with different TPG (p = 1 MPa/m) 图4. 10微米微管中不同启动压力梯度下的流速分布 Figure 5. The flow rate affected by pressure gradient through a channel of 10 um diameter 图5. 10微米微管中启动压力梯度影响的水的流量 3.2. 牛顿流体在低渗透孔孔介质中的渗流模型 对于多孔介质,可以利用毛管束模型分析相应的 渗流公式,定义渗透率为 2 0 8 K r (16) 式中, 为孔隙度,小数。 由(15)和(16)式可得低渗透多孔介质中的公式为 4 0, QK 1, pG A Gp p pG (17) 当启动压力梯度为 0时,我们可以得到达西流的 流量公式, k QAp (18) 最后,以一个例子说明公式(17)的应用。假设原 油在某一维低渗透多孔介质中的流动特征,其过流面 积为 10 m2,渗透率为 0.001 um2,原油粘度为 10 mPa. s ,由 公 式(18)可以计算原油流量随压力梯度的变 化。如图 6所示:在启动压力梯度较小时(Go = 0.1), 流动特征接近于达西渗流的线性流动,当启动压力梯 度较大时,就明显看到小压力梯度下的流量减小,偏 离达西流。说明模型(17)很好地描述了低渗透多孔介 质中的渗流特征。 由图 5和图 6可知:无论对于微管,还是低渗透 多孔介质,方程(15)和(17)都可以很好地描述驱动压力 梯度所有范围内的流量,特别是小压力梯度下下的流 量描述,因此公式可以用于实际的工程计算。 3.3. 新模型的实验验证 3.3.1. 微管中流动的实验 如图 7中为超纯水在直径为5微米石英微管中的 流动数据,经与理论计算结果拟合,得到其启动压力 梯度为 0.014 MPa/m,这个数据对于 50 mm长试验段 微管段,启动压差为 0.0007 MPa,这样的数据在试验 中难以观察,却可以通过理论拟合的方法来估算,也 就是说:公式(15)除了可以预测微管中的流量外,也 可以用于求解液体在微观中流动的启动压力。 3.3.2. 低渗透多孔介质中流动的实验 如图 8中为一低渗透岩心的室内试验渗流数据, 经与理论计算结果拟合,得到其启动压力梯度为 0.006 MPa/m,说明公式(17)除了可以液体在低渗透多孔介 质的流量外,也可以用于求解液体在低渗透多孔介质 中的启动压力梯度。 Figure 6. The flow rate affected by pressure gradient in low per- meability porous media 图6. 低渗透油藏中启动压力梯度影响的流量 Copyright © 2012 Hanspub 33  低渗透油藏渗流模型新解 Copyright © 2012 Hanspub 34 参考文献 (References) [1] 冯文光. 非达西低速渗流的研究现状与进展[J]. 石油勘探与 开发, 1986, 13(4): 76-80. [2] 闫庆来. 低渗透油层中单相液体渗流特征的实验研究[J]. 西 安石油学院学报, 1990, 5(2): 1- 6. [3] 刘志远, 杨正明, 刘学伟. 低渗透油藏非线性渗流实验研究 [J]. 科技导报, 2009, 27(17): 57-60. [4] 吕静, 刘玉章, 李宜坤. 低渗透岩心渗流过程压力传播特征 研究[J]. 水动力学研究与进展A辑, 2010, 25(6): 758-762. [5] 宋付权, 刘慈群, 吴柏志. 启动压力梯度的不稳定快速测量 [J]. 石油学报, 2001, 22(3): 67-70. [6] 朱维耀, 刘今子, 宋洪庆. 低/特低渗透油藏非达西渗流有效 动用计算方法[J]. 石油学报, 2010, 31(3): 452-457. [7] 黄延章. 低渗透油层渗流机理[M]. 北京: 石油工业出版社, 1999. Figure 7. The match of experimental flow rate of water flow in a channel of 5 um diameter 图7. 5微米微管中理论流量和实验的对比 [8] 邓英尔, 刘慈群. 低渗油藏非线性渗流规律数学模 型及其应 用[J]. 石油学报, 2001, 22(4): 72-76. [9] 姜瑞忠. 低渗透油藏非线性渗流理论及数值模拟方法[J]. 水 动力学研究与进展, 2011, 26(4): 444-452. [10] C.-M. Ho, Y.-C. Tai. Micro-Electro- Mech anical -Syst e ms (MEM S) and fluid flows. Annual Review of Fluid Mechanics, 1998, 30: 579-612. [11] M. Gad-el-Hak. The fluid mechanics of microdevices—The free - man scholar lecture. Journal of Fluids Engineering, 1999, 121(5): 5-33. [12] M. Mara Gh., D. Q. Li. Flow characteristics of water in micro- tubes. International Journal of Heat and Fluid Flow, 1999, 20(2): 142-148. [13] Y. Zhu, S. Granick. Limits of the hydrodynamic no-slip bound- ary condition. Physical Review Letters, 2002, 88(10): Article ID: 106102. [14] D. C. Tretheway, C. D. Meinhart. Apparent fluid slip at hydro- phoblic micro-channel walls. Physics of Fluids, 2002, 14: 9-12. [15] 凌智勇, 刘勇, 丁建宁等. 亲水性和疏水性微管道中流动滑 移特性的实验研究[J]. 中国机械工程, 2006, 17(22): 2326- 2329. Figure 8. The match of experimental flow rate of oil flow with theoretical prediction in a low permeability core 图8. 低渗透岩心中理论流量和实验的对比 [16] 叶霞, 周明等. 超疏水光栅微结构表面减阻试验研究[J]. 中 国机械工程, 2007, 18(23): 2779-2785. 4. 结论 [17] R. J. Jiang, F. Q. Song. Flow characteristics of deionized water in microtubes. Chinese Physics Letters, 2006, 23(12): 3305-3308. [18] 王新亮, 狄勤丰等. 超疏水表面滑移理论及其减阻应用研究 进展[J]. 力学进展, 2010, 40(3): 241-248. 本文分析了现有的描述低渗透油层非达西渗流 的模型,从微管的滑移模型出发,推导了具有边界黏 附层的流体在微管中了流量公式,以及低渗透多孔介 质中,考虑边界流体黏附层的渗流模型,并举例进行 了分析。该模型既考虑了压力梯度较小时的流量,又 包含了压力梯度较大时的流动,因此该模型具有较好 的理论和应用价值。 [19] 宋付权, 陈晓星. 液体壁面滑移的分子动力学研究[J]. 水动 力学研究与进展, 2012, 27(1): 80-86. [20] F.-Q. Song, J.-D. Wang. Influence of wettability on poiseuille flow by molecular dynamics simulation. Journal of Hydrody- namics, 2010, 27(2): Article ID: 024704. |