Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30408
,
7
pages
10.12677/PM.2019.93059
Research on Chain Regression Point Set on Tent-Like Mapping
Zhanfu Huo, Ziqing Fu
School of Mathematics and Information Science, Guangxi University, Nanning Guangxi

Received: Apr. 29th, 2019; accepted: May 9th, 2019; published: May 24th, 2019

ABSTRACT
The study of chain regression points of continuous self-mapping on metric space has always been an important part of topological dynamical system. This paper mainly studies the dynamic properties of continuous mapping on compact metric, focusing on the characteristics of chain regression points of tent-like mapping.
Keywords:Compact Metric, Continuous Mapping, Tent-Like Mapping, Chain Regression Point
类帐篷映射上的链回归点集研究
霍展福,符子晴
广西大学数学与信息科学学院,广西 南宁

收稿日期:2019年4月29日;录用日期:2019年5月9日;发布日期:2019年5月24日

摘 要
一直以来,对度量空间上连续自映射的链回归点研究是拓扑动力系统的一个比较重要的内容。本文主要研究紧致度量上连续映射的动力性质,重点研究了类帐篷映射的链回归点的特征。
关键词 :紧致度量,连续映射,类帐篷映射,链回归点

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言与预备知识
定义1.1 [1] 我们把正整数集记为 , 称为自然数集。
定义1.2 [2] 设X是一个集合,记刻划X中所含元素数量的概念为基数,记为 .如果X是空集或者存在正整数 ,使得集合 和集合 之间有一个一一映射,则称集合X是一个有限集。
定义1.3 [3] 在度量空间 中,定义公式 为x的一个 -邻域。
定义1.4 [4] 设 是两个度量空间, 。若对于 的任何一个球形邻域 ,存在 某一个球形邻域 ,使得 ,则称f在点 处连续。若f在X的每一点处都连续,则称f是一个连续映射。
定义1.5 [5] 设 为动力系统, ,称集合 为x在f之下的轨道,记为 或 。
定义1.6 [6] 设 为动力系统。对 ,如果对任意 ,存在自然数m和有限点列 ,使得 且 ,则称此点列是从 到 的一个 链,则称点 为f的一个链回归点,f所有的链回归点构成的集合称为链回归点集,记为 。
定义1.7 [7] 设 是集合X到自身的一个映射,记“ ”其中id表示恒同映射,我们称 为f的n次迭代。
定义1.8 [8] 我们把类帐篷映射定义为:
当 时, ,当 时, 。记 为 的不动点,记 为 在 上的斜率, 为 在 上的斜率。 。本节主要讨论 时的情形,当 时,记 ,,则 ,且 。
2. 相关引理
引理2.1:对任意的 ,及 ,若 ,则 。
证明:因为 ,所以 ,,而 ,所以 (*)。另一方面,因为 ,令 。所以 且 。因为 在同一条直线上 ,所以,我们可得 ,由 得 从而 。同样由 得 (**)。所以由(*),(**)得, 。
引理2.2:对任意的 ,及 ,存在 ,使 。
证明:若
,则由引理2.1知
,若对某一个
,当
时,
,当
时,
且
使得
且
。所以
因为
,所以若不存在n,使得
,则
,这与
矛盾。所以存在
,使得
且当 时,
时, 。记
。记 。所以
。所以 。因为
。因为 ,所以存在
,所以存在 ,且
,且 ,使得
,使得 。
。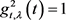 ,
, (1)。由于
(1)。由于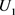 是
是 的
的 邻域,所以存在
邻域,所以存在 。使得
。使得 ,即
,即 ,所以
,所以 。
。
因为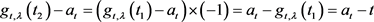 。所以
。所以
 。因为
。因为 ,所以存在
,所以存在 ,使得
,使得 ,所以
,所以 ,
, (2),由(1),(2)知
(2),由(1),(2)知 所以
所以 ,证明完毕。
,证明完毕。
命题2.1:对任意的 ,及
,及 ,存在从
,存在从 到x的关于
到x的关于 的
的 链。
链。
证明:设 ,由引理2.2,存在n,使得
,由引理2.2,存在n,使得 所以存在
所以存在 ,使得
,使得 ,记
,记 。则
。则 是一条从
是一条从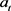 到x的关于
到x的关于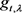 的
的 链。
链。
引理2.3:对任意区间U,若 ,则
,则 ,其中
,其中 。
。
证明:不妨设 ,则
,则 ,
, ,所以
,所以 ,又
,又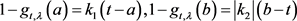 。若
。若 。则
。则 ,因而
,因而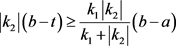 。若
。若 ,则
,则 ,同样有
,同样有 ,由此可得
,由此可得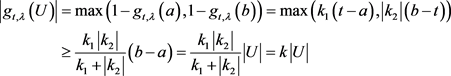 。
。
命题2.2:设 ,若U为一个区间满足
,若U为一个区间满足 且当
且当 时,
时, 。则
。则 ,其中
,其中 。
。
证明:不妨设 ,则
,则 且
且
情形1: 。此时由引理2.3
。此时由引理2.3 ,此时
,此时 ,其中
,其中 。所以
。所以
 ,所以
,所以 。
。
显然上式关于 单调增加,
单调增加, 。
。
所以 。
。
因为 ,所以
,所以 ,另一方面,当
,另一方面,当 时,
时, 关于t单调增加,所以
关于t单调增加,所以
 ,因为
,因为 ,所以
,所以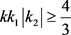 ,即有
,即有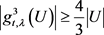 。
。
情形2,若 ,则
,则 ,进一步
,进一步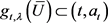 ,则
,则 且
且 ,若
,若 ,则
,则 ,且
,且 ,因为
,因为 ,所以
,所以 ,所以
,所以 。
。
情形3,若 。则
。则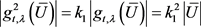 。
。
进一步,若 ,则
,则 。
。
若 ,则
,则 。
。
若 ,则由引理2.3,
,则由引理2.3,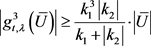 。
。
此时存在 ,使得
,使得 ,即有
,即有
 ,所以
,所以 ,因为
,因为 ,即
,即 ,所以
,所以 或
或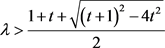 。
。
因为此时 ,所以
,所以 (舍去)。
(舍去)。
所以 。
。
考虑当 时,
时, 。
。
当 时,
时, ,所以
,所以 。从而
。从而 。
。
又当 时,
时, ,当
,当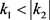 时,
时,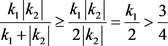 。
。
因为 ,所以
,所以 。
。
取 ,则
,则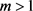 ,且由情形1~3知
,且由情形1~3知 。
。
命题2.3:设 ,若U为一个区间满足
,若U为一个区间满足 ,且
,且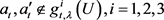 则
则 。
。
证明:因为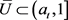 ,所以
,所以 且
且 ,从而
,从而
 .
.
情形1 ,则
,则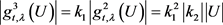 ,因为
,因为

所以 。
。
情形2 ,则
,则 。
。
因为 ,所以
,所以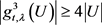 。
。
情形3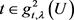 ,此时由引理2.3知,
,此时由引理2.3知,
由情形1~3知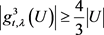 。
。
命题2.4:设 ,U为一个区间满足:
,U为一个区间满足: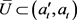 且
且 。
。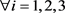 ,
, ,则
,则 。
。
证明:由引理2.3, 且存在
且存在 ,使得
,使得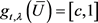 ,所以
,所以 且
且 ,所以
,所以
 .
.
命题2.5:设 ,U为一个区间满足:
,U为一个区间满足: 且
且 ,
, ,则
,则 。
。
证明:在命题条件下,我们有 且
且 ,因为
,因为 且
且 ,所以
,所以 。由命题2.3的证明过程知
。由命题2.3的证明过程知 。
。
命题2.6:设 。则存在
。则存在 。使得
。使得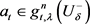 。
。
证明:若结论不成立。则对于任意的 。
。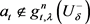 ,
, 。对每一个
。对每一个 ,
, 有下列五种情况:
有下列五种情况:
① ;②
;② ;③
;③ ;④
;④ ; ⑤
; ⑤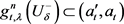 且
且 ;
;
针对情形①②,我们由命题2.2得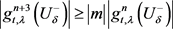
针对情形③,我们由命题2.5得
针对情形④,我们由命题2.3得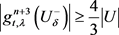
针对情形⑤,我们由命题2.4得
因此,任意的n, ,
, 且
且 。所以
。所以 ,这与
,这与 矛盾.所以结论成立,即存在
矛盾.所以结论成立,即存在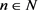 ,使得
,使得 。
。
命题2.7:对对任意的非退化闭区间U,当 时,存在无穷多个
时,存在无穷多个 使得
使得 。
。
证明:若结论不成立,则存在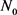 ,对任意的
,对任意的 我们有
我们有 或
或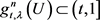 若
若 则
则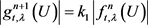 ,若
,若 则
则 ,令
,令 于是对于任意的
于是对于任意的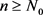 ,我们有
,我们有 ,从而
,从而 ,矛盾。
,矛盾。
命题2.8:设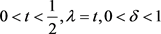 。则存在
。则存在 。使得
。使得 。
。
证明:若结论不成立,则对任意的 ,
, ,
,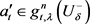 ,有前面引理知,存在
,有前面引理知,存在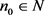 ,使得
,使得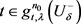 ,所以
,所以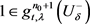 ,
,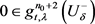 ,
, ,
, ,
,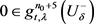 ,
, ,归纳得
,归纳得 ,
, ,
,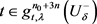 ,
, 因为任意的
因为任意的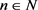 ,
,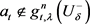 ,
, ,所以
,所以 ,
,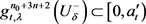 ,
,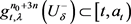 。所以任意的
。所以任意的 ,
,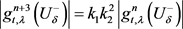 因为
因为 ,所以
,所以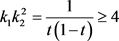 ,所以
,所以 所以
所以 ,矛盾。所以结论成立。
,矛盾。所以结论成立。
命题2.9:设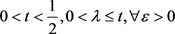 ,
, ,存在从x到
,存在从x到 的关于
的关于 的
的 链。
链。
证明:由 的连续性知,对任意的
的连续性知,对任意的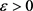 ,存在
,存在 ,当
,当 时,
时, 。由引理命题2.6和命题2.7知:任意满足
。由引理命题2.6和命题2.7知:任意满足 的正数
的正数 ,存在
,存在 ,使得
,使得 。所以,对任意的
。所以,对任意的 ,总存在
,总存在 使得
使得 则对于链
则对于链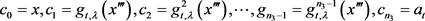 ,有
,有 ,则
,则 是一条从x到
是一条从x到 的
的 链。命题得证。
链。命题得证。
3. 主要定理的证明
定理3.1: ,
, 。
。
证明:当 时,任意的
时,任意的 ,由命题2.9知,存在从x到
,由命题2.9知,存在从x到 的关于
的关于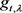 的
的 链,又由命题2.1知对任意的
链,又由命题2.1知对任意的 ,及
,及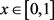 ,存在从
,存在从 到x的关于
到x的关于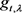 的
的 链,所以
链,所以 。
。
文章引用
霍展福,符子晴. 类帐篷映射上的链回归点集研究
Research on Chain Regression Point Set on Tent-Like Mapping[J]. 理论数学, 2019, 09(03): 441-447. https://doi.org/10.12677/PM.2019.93059
参考文献
- 1. 孙太祥, 席鸿建, 张更容, 陈占和. 树映射的动为学[M]. 南宁: 广西科学技术出版社, 2011.
- 2. 廖公夫, 王立冬, 范钦杰. 映射迭代与混純动力系统[M]. 北京: 科学出版社, 2013.
- 3. 赵俊玲. 强链回归点及跟踪性[J]. 数学学报, 2004, 37(3): 286-291.
- 4. 陆卫风. 帐篷映射的动力系统[J]. 苏州职业大学学报, 2004, 15(1): 65-67.
- 5. 巧火云, 卢建平. 区间上帐篷映射的强混合性[J]. 华东交通大学学报, 2000, 17(3): 75-78.
- 6. 熊金城. 点集拓扑讲义[M]. 北京: 高等教育出版社, 1997.
- 7. 张景中, 熊金诚. 函数迭代与一维动力系统[M]. 成都: 四川教育出版社, 1992.
- 8. 叶向东, 黄充, 邵松. 拓扑动力系统概论[M]. 北京: 科学出版社, 2008.