Operations Research and Fuzziology
Vol.
14
No.
02
(
2024
), Article ID:
84351
,
12
pages
10.12677/orf.2024.142134
基于上证50ETF的期权定价实证研究
王茜
武汉科技大学理学院,湖北 武汉
收稿日期:2024年1月17日;录用日期:2024年2月7日;发布日期:2024年4月12日

摘要
期权作为一种金融工具,期权的存在不仅使投资者在风险管理和制定投资策略方面更具灵活性,同时也为其提供了一种获利的机会。因此,如何对期权进行科学、有效的定价就显得尤为关键。为满足这一需求,学者们提出了多样化的期权定价模型,以确保更准确地反映市场状况和更有效地进行风险管理。本文以上证50ETF期权为研究对象,采用B-S期权定价模型、蒙特卡洛定价模型以及Heston模型对其进行定价,并对三种模型下的期权定价结果进行了全面对比分析。其中,Heston模型采用模拟退火算法,准确地估计出了5个参数。研究结果显示,与B-S定价模型和蒙特卡洛定价模型相比,Heston模型具有更小的误差。这进一步验证了Heston模型更加准确和有效地模拟上证50ETF期权价格的能力。然而,在模拟过程中,这三种方法都会产生一定程度的误差。此外,为了有效缩减误差,文章引入了对偶变量技术,结果表明对偶技术在提高模拟效率和减小波动性方面具有显著优势。
关键词
期权定价,B-S模型,Heston模型,模拟退火算法,对偶变量法

Empirical Research on Option Pricing Based on Shanghai 50ETF
Qian Wang
College of Science, Wuhan University of Science and Technology, Wuhan Hubei
Received: Jan. 17th, 2024; accepted: Feb. 7th, 2024; published: Apr. 12th, 2024

ABSTRACT
As a financial instrument, the existence of options not only gives investors more flexibility in risk management and formulation of investment strategies, but also provides them with an opportunity to make profits. Therefore, how to price options scientifically and effectively is particularly critical. To meet this demand, scholars have proposed diverse option pricing models to ensure more accurate reflection of market conditions and more effective risk management. In this paper, we adopt the B-S option pricing model, Monte Carlo pricing model and Heston model to price the CSE 50ETF options, and make a comprehensive comparison and analysis of the option pricing results under the three models. Among them, the Heston model uses a simulated annealing algorithm to accurately estimate five parameters. The findings show that the Heston model has a smaller error compared to the B-S pricing model and the Monte Carlo pricing model. This further validates the ability of the Heston model to more accurately and efficiently simulate SSE 50ETF option prices. However, all three methods generate a certain degree of error during the simulation process. In addition, in order to effectively scale down the error, the article introduces the pairwise variable technique, and the results show that the pairwise technique has significant advantages in improving the simulation efficiency and reducing the volatility.
Keywords:Option Pricing, B-S Model, Heston Model, Simulated Annealing Algorithm, Dual Variable Method

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,中国的金融市场蓬勃发展,金融衍生产品种类更加丰富。金融衍生工具越来越显示出它的实用价值,并在各种金融活动中扮演着举足轻重的角色。期权作为其中之一,拥有独特功能和用途,深入研究期权定价问题具有实质性意义。相较于西方发达国家,我国的金融市场还不够完善,因此,投资者在投资过程中往往要承担很大的风险。基于此,考虑如何利用期权为投资者构建合理的投资组合,减少投资风险尤为关键。因此,深入探讨期权定价问题对于实际投资指导具有重要的意义。
在金融领域,对期权定价问题一直有着深入的研究,许多学者在这一领域进行了广泛的调研。在1973年中,Black-Scholes提出了建立B-S期权定价模型的方法,揭开了现代期权定价的“面纱” [1] 。纪琼(2015)在研究中分别使用GARCH和BS模型对上证50ETF期权价格进行了模拟,研究结果发现在GARCH模型具有一定的改进效果 [2] 。过去的研究表明,学者们通常假设标的资产的价格运动遵循布朗运动模型。然而,标的资产价格的运动在实际中常有自相似性,这使得传统的布朗运动模型在描述实际市场的复杂动态时存在局限性。
宋海明和侯頔(2021)基于Black-Scholes模型并结合神经网络算法设计了新的期权定价模型,并验证了该算法的有效性 [3] 。在一项研究中,于长福和陈婷婷(2016)采用了上证50ETF的历史波动率作为期望波动率,并利用B-S模型来实现期权定价 [4] 。另外,方艳等(2017)使用GARCH和IGARCH模型两种模型分别对上证50ETF的波动率进行了预测,然后分别运用蒙特卡罗法和B-S模型对上证50ETF进行了期权定价 [5] 。然而,以上模型中都将期望波动率当作常数,这使得以往构建的模型存在一定局限性。
为了克服这些局限性,邓国和(2012)创新地将波动率视为时变函数并结合Heston模型 [6] 。然而,Heston模型的参数众多且难以解决,王林等人(2011)选择了使用模拟退火算法来估算Heston模型的5个参数,从而成功地解决了参数解决的问题 [7] 。而在李斌等人的研究中(2015),使用遗传算法对模型中的一些复杂参数进行了组合优化 [8] 。在张丽娟等人的研究中(2018),首先使用Heston模型对期权进行了定价,接着通过神经网络模拟实际期权价格与模拟价格之间的差异。最后,他们运用遗传算法对整个神经网络进行优化,从而提高了模型的性能和适应性 [9] 。刘莹和郑玉衡(2019)利用粒子群智能优化算法对Heston模型中的参数进行估计,研究结果发现采用粒子群优化算法的Heston模型期权定价模型效果更好 [10] 。
本研究以上证50ETF为研究对象,采用B-S模型、蒙特卡洛期权定价模型以及Heston模型来确定期权的价格。针对Heston模型中的五个参数,我们使用模拟退火算法进行了预测。本研究对三种模型在看涨和看跌期权定价上的表现进行了对比分析,并给出了优化意见。
2. 期权定价模型与优化算法
2.1. B-S定价模型
B-S定价模型看涨期权和看跌期权的价格分别为:
 (1)
(1)
(2)
系数 和 满足
(3)
(4)
其中,C和P分别代表欧式看涨期权和看跌期权的价格,S表示t时刻标的资产的价格,r表示无风险利率, 表示合约的剩余期限,K表示执行价格,T表示合约的到期日,σ表示标的资产的波动率, 则指的是累积标准正态分布函数。
2.2. 蒙特卡洛定价模型
蒙特卡洛模拟期权定价是一种基于随机模拟的数值方法,用于评估期权合约的价格,其步骤如下:
1) 设定模型参数:确定资产价格的随机演化模型,包括初始价格 、执行价格K、无风险利率r、波动率σ、剩余期限 等。
2) 初始化:设置模拟路径的数量N,设定时间步长 。
3) 生成路径:对于每一条模拟路径i:首先生成标准正态分布随机数 ,然后利用资产价格演化模型计算资产价格路径: 。
4) 计算期权收益:对于每条模拟路径i,根据期权类型(看涨或看跌)计算期权到期时的收益:欧式看涨期权: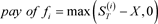 ,欧式看跌期权
。
,欧式看跌期权
。
5) 计算期望收益:对所有模拟路径的期权收益取平均值,得到期望收益为 。
6) 折现期望收益:利用无风险利率将期望收益折现到当前时刻,即
7) 计算期权价格:得到的折现期望收益即为期权的估计价格。
2.3. Heston模型
Heston模型形式如下:
(5)
(6)
(7)
在这个模型中, 是价格过程, 是方差过程。 是一个无法被观测的状态变量,符合均值回复平方根CIR过程。其中, 表示股票价格的均值;参数 表示非负常数。 为均值回归速率; 为波动率的方差; 为长期方差; 和 代表布朗运动的过程; 则是两个布朗运动的相关系数。
基于以上信息,求解得出Heston模型的定价公式:
(8)
这里:
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
其中, , ,欧式标准期权的执行价格和到期日分别用K和T表示,r表示年利率,而λ则是指波动率风险的市场价格。
2.4. 模拟退火算法
面对复杂的金融模型,如Heston模型,解决参数估计问题时常需要应对非线性最小二乘的挑战。在这一背景下,模拟退火算法备受推崇,它作为一种全局优化算法,通过引入随机性的手段,有助于跳脱出局部最小值,以期望找到全局最小值。在针对本文的Heston模型中,模拟退火算法优化参数的主要步骤包括:
1) 指定退火温度 ,将初始解 代入目标函数 得到 ,其中:N为样本量; 为通过Heston模型得到的期权定价; 为第i个样本的市场期权实际价格; 为需要优化的参数集合。
2) 当处于状态i时,参数集表示为 。通过微小扰动状态i,得到状态j的参数集 。如果在扰动后的状态j下,目标函数值 小于状态 下的目标函数值 ,则接受新的状态j;否则,以一定概率接受新状态i。换句话说,转移的概率为:
(20)
其中T表示当前温度,k表示常数。
3) 当温度不再满足迭代条件时,则降低温度并继续进行迭代。
4) 若温度不能继续下降,则模拟退火算法完成。
模拟退火算法的流程如图1所示。
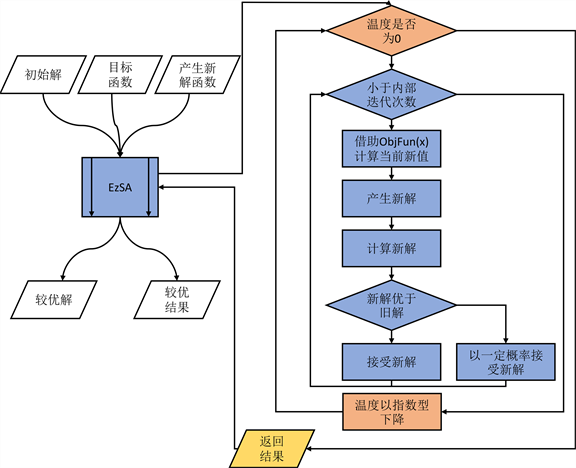
Figure 1. Flow chart of simulated annealing algorithm
图1. 模拟退火算法流程图
3. 数据选取与统计描述
选取标的资产上证50ETF从2022年1月5日至2022年12月30日共241个交易日的日收盘价数据进行研究,对数收益率计算公式为 ,数据的统计特征如表1所示。
Table 1. 50ETF logarithmic return statistical eigenvalue
表1. 50ETF对数收益率统计特征值
通过表1中我们可以观察到,上证50ETF的对数收益率的分布偏度为−0.030121585 < 0,这表明它具备左偏的特征。峰度为4.2462173 > 3,这表明它具备了显著的尖峰和厚尾的属性。
绘制上证50ETF的对数收益率的正态分布拟合图和QQ图如图2、图3所示:

Figure 2. Shanghai stock exchange 50ETF log-return of the normal distribution of the fitting chart
图2. 上证50ETF的对数收益率的正态分布拟合图

Figure 3. Q-Q chart of logarithmic yield of Shanghai 50ETF
图3. 上证50ETF的对数收益率的Q-Q图
通过观察图2和图3可得知,上证50ETF的对数收益率具有尖峰厚尾的非正态分布特征。将对数收益率序列进行JB检验,其统计量的值为181.091,P值小于0.001,因此拒绝原假设,这表明数据不服从正态分布。
4. 实证分析
4.1. 参数设置
针对三种不同的模型,我们对上证50ETF的看涨和看跌期权进行了理论价格的计算,考虑了期权定价公式中的相关参数:上证50ETF的当前价格 、期权合约的剩余时间τ、无风险利率r和波动率 。我们选取2022年7月1日至8月24日的交易数据作为样本数据。
1) 上证50ETF的现价
以 表示上证50ETF的闭市价。根据样本数据,由于2022年8月24日是上证50ETF的交易日,因此它的当前价格就是上一个交易日的闭市价格,即 。
2) 上证50ETF期权合约的到期期限
由于我们选取的是截止日期为2022年12月30日的上证50ETF期权,当前时刻假设为2022年8月24日,以交易日计算,该期权的剩余期限为85天,即τ = 85/252 = 0.337。
3) 无风险利率
以1年期上海银行间同业拆放利率(Shibor)为基准进行计算。计算得到在上证50ETF期权交易日期内的1年期Shibor的算术平均值:
依据普通复利和连续复利的转换公式,无风险连续复利利率为 。
4) 上证50ETF波动率
使用历史波动率方法来估计上证50ETF的收益率波动率 [1] 。根据表1,计算得到上证50ETF在2022年7月1日至8月24日期间的日对数收益率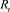 ,其中
。对于上证50ETF的历史波动率的估计,我们必须对样本方差进行计算,即
,在这里
,代表上证50ETF日对数收益率的均值。经过运算,我们获得样本标准差为
,即上证50ETF的每日波动率。若将中国的股票市场视作一年存在252个交易日,则可以计算出上证50ETF的年波动率,这个年波动率为0.138。
,其中
。对于上证50ETF的历史波动率的估计,我们必须对样本方差进行计算,即
,在这里
,代表上证50ETF日对数收益率的均值。经过运算,我们获得样本标准差为
,即上证50ETF的每日波动率。若将中国的股票市场视作一年存在252个交易日,则可以计算出上证50ETF的年波动率,这个年波动率为0.138。
4.2. 基于B-S模型、MC方法、Heston模型的上证50ETF期权价格实证分析
进行1000次Python模拟,获取了上证50ETF看涨和看跌期权价格的相关数据,详细信息请参见表2和表3。
通过观察表2和表3的数据,可以发现无论是看涨期权还是看跌期权,三种模型的定价结果都与市场价格非常接近。此外,随着执行价格的增高,看涨期权的价格出现下滑的趋势,反之,看跌期权的价格则呈上升趋势。
从表4的结果可以观察到,对于这三个指标,Heston模型的数值最小,其次是蒙特卡洛模拟(MC),而B-S定价模型的数值最大。这表明在考虑期权实际成交价格的情况下,Heston模型在绝对平均误差、平均绝对相对误差和均方根误差方面都表现出更小的偏差,与蒙特卡洛期权定价方法和B-S定价模型相
Table 2. Call option pricing information sheet
表2. 看涨期权定价信息表
Table 3. Put option pricing information sheet
表3. 看跌期权定价信息表
Table 4. Evaluation of pricing effectiveness
表4. 定价效果评估
比,它具有更高的精度。因此,从这三个指标综合考虑,Heston模型在期权定价中展现出更高的准确性,蒙特卡洛期权定价方法次之,B-S定价模型准确性最低。相较于传统的B-S模型和蒙特卡洛模拟期权定价,Heston模型的定价结果更接近实际值。换言之,Heston模型在期权定价方面表现出更高的准确性和可靠性。图4和图5分别展示了在三种模型下看涨和看跌期权的实际市场价格与理论价格的对比,表明了它们之间的显著差异,从而进一步验证了Heston模型的优越性。
上证50ETF看涨期权的价格在三种模型中表现得基本一致,然而,在Heston模型中,看跌期权的价格更接近真实的市场价格。因此,Heston期权定价模型能够更准确和有效地模拟实际的期权价格。这与使用MAE、MAPE、RMSE评价标准所得的结论一致。
运用模拟退火算法对Heston模型参数进行估计,有助于更精确地拟合市场观察数据。将模拟退火算法的初始温度设置为90℃,允许达到的最低温度为1e−06℃,初始参数集为 ,最大迭代次数为400次,新旧最优值之差绝对值连续小于0.001达到100次时,终止该温度循环。表5中所示的参数即为通过该算法得到的结果。
Table 5. The optimal parameter table of Heston model based on simulated annealing algorithm
表5. 基于模拟退火算法Heston模型的最优参数表
随后,我们使用获得的参数对上证50ETF的看涨期权和看跌期权进行定价,具体展示在图4和图5中。可以发现通过Heston模型可以更准确地估计期权价格,以更好地反映市场实际情况。
4.3. 对蒙特卡洛模拟方法的改进
在上述模拟过程中,主要采用了蒙特卡洛方法,该方法具有高度可移植性和操作简便等优势。在足够大的样本容量下,蒙特卡洛模拟可以使得结果总能够向真实值收敛。然而,该方法也存在一些明显的不足之处。首先,计算效率相对较低,方差减小速度较慢。其次,在实际生成随机数的过程中,采用的是伪随机数。这些伪随机数无论采用何种生成方法,都是从一个有限长度的集合中不断循环生成的,因此导致模拟的价格序列并非真正的随机游走序列,可能引入一定的偏误。
为了有效解决上述问题,采用方差缩减技术是提高模拟稳定性、减少模拟次数的有效途径。在本文中,选择了对偶变量技术作为方差缩减的手段。以2022年12月到期、行权价2.514元的50ETF欧式看涨期权为例,该合约在8月24日的交易日价格为2.774元。首先,使用B-S公式直接计算得到该期权的理论价格为0.2873。接下来,分别采用一般的B-S模型蒙特卡洛模拟和对偶变量法的蒙特卡洛模拟,比较它们逼近B-S值的效率。
表6呈现了一般的B-S模型蒙特卡洛模拟和对偶变量法蒙特卡洛模拟的计算结果。
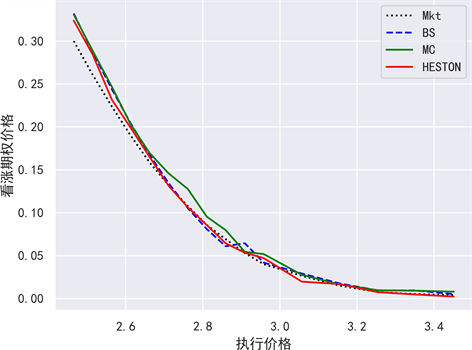
Figure 4. Price comparison chart of call options
图4. 看涨期权价格对比图
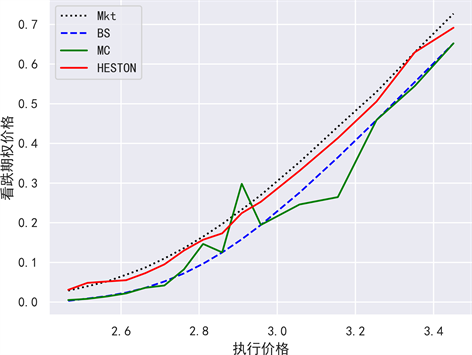
Figure 5. A chart of put options prices
图5. 看跌期权价格对比图
表6显示了随着模拟路径数量的增加,与传统的蒙特卡洛模拟技术相比,采用降方差技术能够更快地逼近理论值。在此,我们将每条路径的模拟步数设置为100步,表格中的序列数表示生成模拟路径的数量。采用相对误差来度量模拟值和理论值之间的相对偏差,以百分比表示,计算公式为 。
Table 6. Effect reduction by dual variable method
表6. 对偶变量法缩减效果
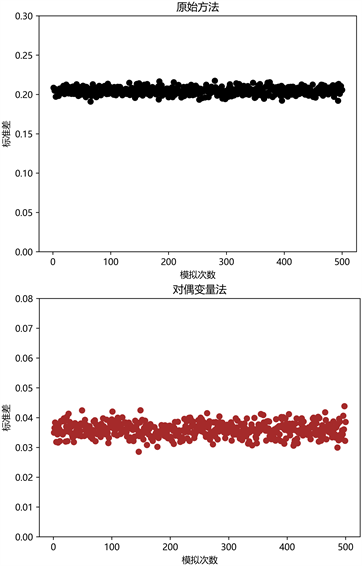
Figure 6. A comparison of the original method and the dual variable method
图6. 原始方法和对偶变量法的对比图
通过表6,可以观察到采用降低方差的技术后,随着模拟路径数量的增加,模拟值与理论值之间的偏差逐渐减小。与此同时,相对误差的变动速率也明显低于采用常规蒙特卡洛方法进行的变动速率。为使此结果更加直观,图6呈现了随着模拟次数的增加,原始方法和对偶变量法的标准差的对比情况。图中每个点都代表进行10次模拟得到的标准差。通过对比散点图,可以清晰地观察到在相同的模拟次数下,使用对偶变量法的方差缩减效果更为显著,特别是在模拟次数为500时。因此,随着模拟次数的增加,采用对偶技术后的模拟价格更迅速地接近真实价格,同时模拟结果也更为稳定。这凸显了对偶技术在提高模拟效率和减小波动性方面的显著优势。
5. 结论
本文选取上证50ETF期权作为研究对象,并运用B-S定价模型、蒙特卡洛定价模型和Heston模型来对其进行定价分析。在Heston模型中,通过应用模拟退火算法,成功精准估算了5个参数。研究结果表明,Heston波动率模型在接近期权实际成交价格时表现出较小的误差,其次是蒙特卡洛期权定价方法,而B-S定价模型的误差最大。这说明Heston模型在模拟上证50ETF期权价格方面具有更准确、更有效的优势。然而,在模拟过程中,这三种方法都存在一定的误差。为了有效缩减误差,采用了对偶变量技术。结果显示,对偶技术在提高模拟效率和减小波动性方面具有显著优势,具有更好的收敛性。综合而言,采用对偶变量技术可以在提高期权定价模型的准确性和效率的同时,有效地减小模拟误差,改善期权定价模型的性能。
文章引用
王 茜. 基于上证50ETF的期权定价实证研究
Empirical Research on Option Pricing Based on Shanghai 50ETF[J]. 运筹与模糊学, 2024, 14(02): 284-295. https://doi.org/10.12677/orf.2024.142134
参考文献
- 1. Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81, 637-654. https://doi.org/10.1086/260062
- 2. 纪琼. 上证50ETF期权的定价研究[J]. 经营管理者, 2015, 29(24): 23-24.
- 3. 宋海明, 侯頔. Black-Scholes模型下美式期权定价的神经网络算法[J]. 吉林大学学报(理学版), 2021, 59(5): 1089-1092.
- 4. 于长福, 陈婷婷. 基于B-S模型的上证50ETF期权定价的实证研究[J]. 金融理论与教学, 2016(2): 7-11.
- 5. 方艳, 张元玺, 乔明哲. 上证50ETF期权定价有效性的研究: 基于B-S-M模型和蒙特卡罗模拟[J]. 运筹与管理, 2017, 26(8): 157-166.
- 6. 邓国和. Heston模型的欧式任选期权定价与对冲策略[J]. 广西师范大学学报(自然科学版), 2012, 30(3): 36-43.
- 7. 王林, 张蕾, 刘连峰. 用模拟退火算法寻找Heston期权定价模型参数[J]. 数量经济技术经济研究, 2011, 28(9): 131-139, 153.
- 8. 李斌, 何万里. 一种寻找Heston期权定价模型参数的新方法[J]. 数量经济技术经济研究, 2015(3): 129-146.
- 9. 张丽娟, 张文勇. 基于Heston模型和遗传算法优化的混合神经网络期权定价研究[J]. 管理工程学报, 2018, 32(3): 142-149.
- 10. 刘莹, 郑玉衡. 使用粒子群算法解决期权定价模型参数校准问题——以Heston模型为例[J]. 科学决策, 2019(12): 34-46.
