Advances in Applied Mathematics
Vol.
11
No.
05
(
2022
), Article ID:
51531
,
12
pages
10.12677/AAM.2022.115278
带三参数的三次B样条扩展曲线及其应用
秦凌云,沈洋,段卓,杨雪
辽宁师范大学数学学院,辽宁 大连
收稿日期:2022年4月18日;录用日期:2022年5月13日;发布日期:2022年5月23日

摘要
为满足曲线自由设计的需求,本文对 -B样条基和三次T-B样条基进行扩展,构造了 -T-B样条基函数,定义了由该基函数生成的 -T-B样条曲线,其中含有三个参数 、 、 ,构造的曲线不仅具备样条曲线的特性,还同时具备三角和代数多项式的优良性质,且具有形状可调性和更精确的逼近性;在给定条件下,形状参数有明确的几何意义, 、 取值越大, 值越小,越能更好地逼近控制多边形;调节参数的取值,改变曲线的形状;选则恰当的控制顶点,根据参数对曲线的调节规律,确定恰当的形状参数,生成的 -T-B样条曲线能较好贴近圆和椭圆;介绍了生成插值于给定数据点的 -T-B样条曲线的构造方法,并给出具体数例的计算,验证了方法的有效性和可行性。
关键词
样条曲线,形状参数,曲线设计,逼近,插值

Cubic B-Spline Extension Curve with Three Parameters and Its Application
Lingyun Qin, Yang Shen, Zhuo Duan, Xue Yang
School of Mathematics, Liaoning Normal University, Dalian Liaoning
Received: Apr. 18th, 2022; accepted: May 13th, 2022; published: May 23rd, 2022

ABSTRACT
In order to meet the requirement of free curve design, this paper extends the -B-spline basis and cubic T-B-spline basis and constructs a group of -T-B-spline basis function. The -T-B-spline curve generated by the base function is defined, which contains three parameters ,, and , has the characteristics of spline basis function, but also has the good properties of trigonometric and algebraic polynomial basis, and has the shape tunability and more accurate approximation; under given conditions, shape parameters have clear geometric meaning. The larger the value of and , the smaller the value of , the better the approximation control polygon can be. By changing the value of shape parameters, the curve can be adjusted; by selecting the appropriate control vertex and the appropriate shape parameters, the generated -T-B-spline curve can approach the circle and ellipse very well; In the end, the method of constructing -T-B-spline curve interpolating in the data points is introduced, and the calculation of specific numerical examples is given, reflect the effectiveness and feasibility.
Keywords:Spline Curve, Shape Parameters, Curve Design, Approximation, Interpolation

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
B样条在计算机辅助几何设计中一直处于重要地位,由于其结构简单又具有灵活性,在工程实际中应用较为广泛,在文献中也有较多讨论与研究。但在曲线形状调整这一方面一直需要改进,若需调节所生成的曲线,通常仅能通过调节控制顶点来完成,这也带来些许不便。因而,不断有新的构造方法被提出。
为扩大B样条形状表示范围,学者们选择利用多项式空间 [1] [2] [3] [4] 与非多项式空间 [5] [6] [7] 进行混合,构造与B样条基类似的调配函数 [3],由此定义的曲线的适用性有很大提高。在调配函数中,全正性 [8] 是衡量是否适用保形的标准。较多学者在过渡曲线 [9] 的基础上,将带形状参数的基函数与转换矩阵做乘积得到扩展基,证明全正性,以确定扩展基定义扩展曲线 [5] [10] - [15]。因多项式曲线的计算更为简单,可以较好地融入CAD系统。所以大多学者选择在多项式曲线上构造带有形状参数的B样条扩展曲线。利用三次或以上的调配函数,增加阶数达到形状可调性,构造的含参扩展曲线 [1] [16],在一定条件下,能够逼近但不能精确表示圆和椭圆。
本文在 基 [1] 和三次T-B样条基 [5] 的基础上,给出了包含三个形状参数 的三次均匀B样条扩展曲线,其中。新构造的 样条曲线保持了B样条曲线的特性,同时拥有三角和代数的优质性质,具有形状可调性和更精确的逼近性。在给定条件下,形状参数 有明确的几何意义,取值越大,越能更好的逼近控制多边形。且当 的时,曲线退化为 曲线 [1];当 的时,退化为三次T-B样条曲线 [5];当 ,,则退化为三次均匀B样条曲线。在给定恰当的控制顶点下,对 做适当取值,生成的 样条曲线能够更好地贴合圆和椭圆。最后,介绍了利用 样条曲线生成基于给定数据点的插值曲线的方案,并给出具体数例的计算,体现了新构造方法的有效性和可行性。
2. -T-B样条基函数的构造及性质
定义1 对 ,令
(1)
其中 ,,。
称(1)式为 样条基函数。
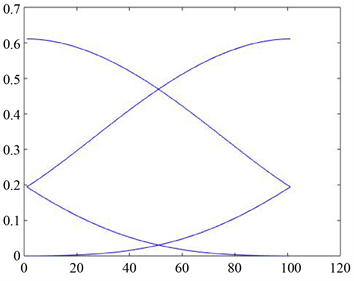
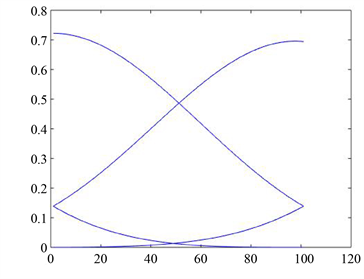
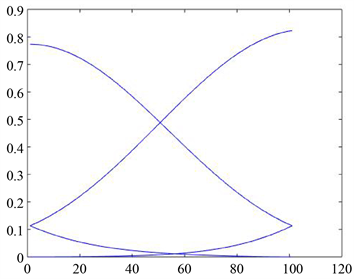
其中三个参数 取值不同时,基函数所对应图形也不同,如图1所示。
图1. 样条基函数所绘制的图形
式(1)所表示的 样条基函数有如下的性质:
性质1 退化性
当 的时候式(1)则退化为 样条基 [1];当 的时候式(1)则退化为三次T-B样条基 [5];当 , 式(1)则退化为三次均匀B样条基。
性质2 非负性
对任意的 ,,,,有 ,。
性质3 规范性
。
性质4 对称性
。
性质5 端点性质
记 ,此时 。且当 时,有 ,。则
3. -T-B样条曲线的构造以及性质
定义2 给定控制点 ,均匀节点向量 ,这里有 ,其中参数 ,,,对 ,能够定义一条多项式曲线段
(2)
因此这个曲线段构成样条曲线
(3)
这里 。我们定义(2)式为 样条曲线段,(3)式为 样条曲线。当所有的 都相等时,U为等距节点向量,称对应的曲线为 均匀样条曲线。
显然, 样条曲线,当 的时候式(3)则退化为 曲线 [1];当 的时候式(3)则退化为三次T-B样条曲线 [5];当 , 式(3)则退化为三次均匀B样条曲线。
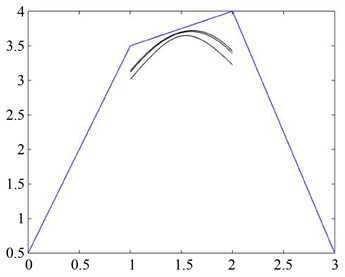
图2为3条 样条曲线,当参数值不一样时,曲线形状也会随之改变。由上至下 分别取值为 ,,。

Figure 2. 3 -spline curves
图2. 3条 样条曲线
由上文中的性质1~5,可以推出 样条曲线的以下性质。
性质6 对称性
由控制点 和 构成的 样条曲线是一样的,形状相同,但方向相反。
性质7 凸包性
由性质2和3可知,曲线位置在控制点生成的凸包之内。
性质8 端点性质
性质9 连续性
当 时, , 时, 。
又因为对 ,有
(4)
所以,
(5)
由(4)和(5)式,可推出
.
当 时, , 时, 。
由此可说明对于 样条曲线,当 时 连续, 时, 连续。
4. 形状参数对曲线的形状的影响
为利用构造曲线设计出满意的形状,需要明确形状参数对曲线形状的影响效果。
1) 确定参数 值,当第三个参数 数值发生变化的时,曲线形状会随 的取值不同而不同。如图3(a)所示。此时 ,曲线从上至下 分别取 。可以看出,当 取值不变时, 值越大,曲线越贴近控制多边形。
2) 确定参数 ,当 发生变化的时,曲线形状会随取值不同而不同。如图3(b)所示。此时 ,曲线从上至下 分别取 。当 取值不变时, 值越小,曲线越贴近控制多边形。
3) 确定参数 ,当 发生变化的时,曲线的位置以及形状就会随之发生改变。如图3(c)所示。此时 ,曲线从上至下 分别取 。当 取值不变时, 值越大,曲线越贴近控制多边形。
图3. 形状参数对曲线的影响
5. 曲线的应用
本文构造的 样条曲线既保留了有理多项式的性质,又保留了三角多项式的性质,可用来表示二次曲线。
5.1. 过首末顶点的闭曲线的设计
若 样条曲线的控制点满足条件 ,, 取任意值,都有 ,。所以当令 样条曲线经过控制多边形 的首末顶点,需增加两个控制顶点 ,,以 为控制定点定义曲线。
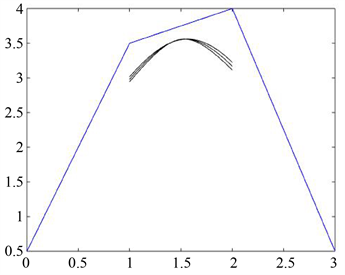
我们要求曲线封闭,则令 ,再增加两个控制点 ,,以 为控制顶点定义曲线。图4为 时过首末控制点的闭曲线。
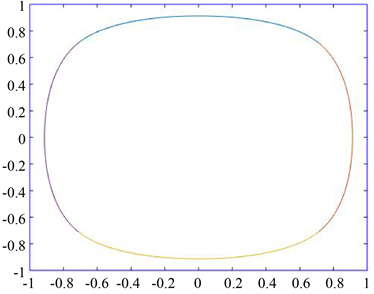
Figure 4. Example of closed curve
图4. 闭曲线实例
5.2. 圆与椭圆的逼近
确定控制点 ,,,,,,,以 为控制顶点的 样条曲线会更加逼近圆 ,图5是 时,曲线对圆的逼近。
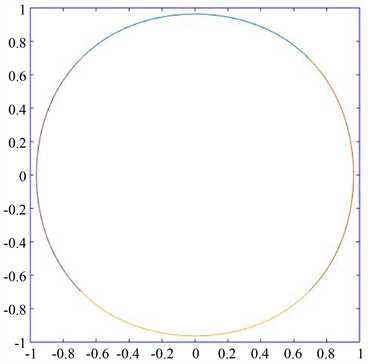
Figure 5. The approximation of the curve to the circle
图5. 曲线对圆的逼近
取定控制点 ,,,,,,,以 为控制顶点的 样条曲线会更加逼近圆 ,图6是 时,曲线对椭圆的逼近。
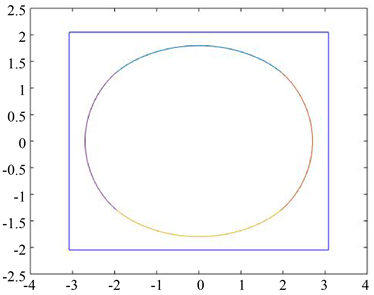
Figure 6. The approximation of the curve to the ellipse
图6. 曲线对椭圆的逼近
5.3. -T-B样条曲线的插值
通常情况下, 样条曲线不过任何一个控制点。当要求 样条曲线插值于n个数据点 ,并插值点与分段曲线的端点相对应,由 样条曲线的端点性质有:
(6)
其中 ,(6)式为含有 个未知数,n个方程的方程组,因此应填加两个端点条件去求解唯一解。
设
(7)
根据式(6)与(7),有
整理得
将式(6)与(7)化为等价的矩阵:
(8)
这里
由(8)式可推出 ,由此,即可以求出控制顶点。
如果插值点是封闭的,则有 ,这样便生成一条封闭,但闭合点处不光顺的插值曲线。如果令 ,,,就可产生一条封闭、光顺的插值曲线。
假如插值点与分段曲线的端点对应,由性质8有:
(9)
上式为含有 个未知数, 个方程的方程组,可求得 个彼此不重复的控制顶点。把(9)式写成等价矩阵:
(10)
其中有
由(10)式可推出 ,即可求出控制顶点。
当 以及 ,此时退化为 曲线。
我们取 时, ,此时 ,
给定 ,便可求出唯一解
6. 总结
本文构造了一个带三个形状参数的 样条曲线,保持了三次B样条曲线的基本性质,并同时具备代数和三角多项式的优良性质,具有更好的逼近性。且能在控制顶点不需改变时,仅调节三参数,便能调整曲线形状。当给定适当的控制顶点以及形状参数时,能更加贴近圆和椭圆。最后给出了利用曲线,生成给定数据点的插值曲线的方案,并给出具体数例计算,增强了本文所构造曲线的适用性质,体现了有效性和可行性。
本文对于曲线推广到曲面的问题上没有进行讨论,为设计出更符合实际需求的造型,仍还需多加研究。
文章引用
秦凌云. 带三参数的三次B样条扩展曲线及其应用
Cubic B-Spline Extension Curve with Three Parameters and Its Application[J]. 应用数学进展, 2022, 11(05): 2629-2640. https://doi.org/10.12677/AAM.2022.115278
参考文献
- 1. 裴芳, 武建. 三次均匀B样条曲线的一种新扩展[J]. 数学的实践与认识, 2019, 49(9): 264-271.
- 2. 严兰兰, 饶智勇, 黄涛. Bézier曲线的同次扩展及其参数选择[J]. 中国图象图形学报, 2018, 23(9): 1411-1423.
- 3. 仇茹, 杭后俊, 潘俊超. 带三参数的类四次Bézier曲线及其应用研究[J]. 计算机工程与应用, 2014, 50(20): 158-162.
- 4. 杭后俊, 余静, 李汪根. 三次Bézier曲线的一种双参数扩展及应用[J]. 计算机工程与应用, 2010, 46(31): 178-180+205.
- 5. 严兰兰, 韩旭里, 黄涛. 带一个形状参数的3次三角多项式曲线曲面[J]. 计算机辅助设计与图形学学报, 2016, 28(7): 1047-1058.
- 6. 耿紫星, 张贵仓. Bézier曲线的三角扩展[J]. 计算机工程与应用, 2008, 44(26): 59-61+134.
- 7. 彭兴璇, 潘晶, 陈雪娇, 蒋新昕. 切点可调的带形状参数的二阶三角Bézier曲线[J]. 图学学报, 2017, 38(4): 463-468.
- 8. 王成伟, 张卷美. 三次Bézier曲线另一种带三参数的新扩展及其应用[J]. 北京电子科技学院学报, 2021, 29(1): 47-53.
- 9. 严兰兰, 樊继秋, 马力. 形状调配中带参数的过渡曲线设计[J]. 图学学报, 2019, 40(2): 379-387.
- 10. Han, X.A., Ma, Y.C. and Huang, X.L. (2009) The Cubic Trigonometric Bézier Curve with Two Shape Parameters. Applied Mathematics Letters, 22, 226-231. https://doi.org/10.1016/j.aml.2008.03.015
- 11. 严兰兰, 韩旭里. 基于全正基的三次均匀B样条曲线的扩展[J]. 图学学报, 2016, 37(3): 329-336.
- 12. 严兰兰, 韩旭里. 三次均匀B样条曲线的保形扩展[J]. 计算机应用研究, 2017, 34(1): 295-301.
- 13. 严兰兰, 韩旭里, 饶智勇. 带局部形状参数的λ-B曲线设计[J]. 中国图象图形学报, 2016, 21(2): 174-183.
- 14. 韩旭里, 刘圣军. 三次均匀B样条曲线的扩展[J]. 计算机辅助设计与图形学学报, 2003, 15(5): 576-578.
- 15. 姬佩佩, 张贵仓, 汪凯, 孟建军. 基于全正基的非均匀三次加权B样条[J]. 中国图象图形学报, 2021, 26(4): 939-951.
- 16. 吴晓勤, 韩旭里. 三次Bézier曲线的扩展[J]. 工程图学学报, 2005, 26(6): 98-102.