Journal of Electrical Engineering
Vol.04 No.01(2016), Article ID:17074,12
pages
10.12677/JEE.2016.41003
Evaluation of Tiered Electricity Pricing Schemes Based on Fuzzy Analytic Hierarchy Process
Jun Hu1, Tianran Li1*, Xusheng Qian2, Liang Ying1, Caihong Zhao1
1School of Electrical and Automation Engineering, Nanjing Normal University, Nanjing Jiangsu
2Nanjing Power Supply Company, Nanjing Jiangsu

Received: Feb. 12th, 2016; accepted: Feb. 26th, 2016; published: Mar. 4th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
A comprehensive evaluation index system for tiered electricity pricing schemes is proposed by applying fuzzy analytic hierarchy process (AHP). The interests of the resident side, social side and supply side are taken into account in index selection. Linear expenditure principle is employed to quantify the evaluation. Fuzzy analytic hierarchy process and relative membership degree values are used to calculate the quantitative assessment of composite indicators, and a real example is given to prove the scientificity and practice manipulability of the evaluation system.
Keywords:Tiered Electricity, Fuzzy Analytic Hierarchy Process, Relative Membership Degree Values, Quantitative Evaluation

基于模糊层次分析法的阶梯电价方案评价
胡骏1,李天然1*,钱旭盛2,应亮1,赵彩虹1
1南京师范大学电气与自动化工程学院,江苏 南京
2江苏省电力公司南京供电公司,江苏 南京

收稿日期:2016年2月12日;录用日期:2016年2月26日;发布日期:2016年3月4日

摘 要
本文提出一种基于模糊层次分析法的阶梯电价方案评价决策体系。该体系在指标选择中考虑了居民侧,社会侧和供电侧三方面的利益。利用线性支出等原理量化评价指标,利用模糊层次分析法,结合相对隶属度值,得到定量评价综合指标,并通过实例计算说明了该评价决策体系的科学性和可操作性。
关键词 :阶梯电价,模糊层次分析法,相对隶属度,定量评价

1. 引言
随着电力改革的深入发展,我国大部分地区开始实行居民阶梯电价机制。这是从三个方面考虑的:一是合理反映用电成本,二是公平负担,三是促进节能减排[1] 。因此,阶梯电价方案设计的科学与否将会对社会发展产生较为深远的影响。
目前,在如何评价阶梯电价方案方面,国内外学者做了一些研究。主要涉及用户响应[2] 、对供电公司利益影响[3] 、对居民消费支出的影响[4] 、对社会福利的影响[5] 以及节电效果[6] 等方面。这些评估研究为单一方案的多因素预期效果或多个方案的单目标决策提供了参考,但未涉及多个方案的多准则决策,而这一问题正是当前阶梯电价政策实施初期亟待解决的基础性问题。
本文针对上述问题建立了阶梯电价多方案多准则定量评价体系。首先对各评价准则选取具有代表性的评价指标,运用线性支出等原理对每个指标进行定量计算,并采用相对隶属度值对其进行模糊评价。再利用模糊层次分析法计算各指标的权重,减少人为因素的影响,给出相对客观的指标权重值。最后,结合相对隶属度,给出各方案的多准则综合评价指标,可为阶梯电价方案的科学决策提供参考依据。
2. 多方案多准则综合评价指标体系
2.1. 指标体系的建立
阶梯电价方案需要考虑到社会各方面的利益。首先,要考虑居民的用电权益,需要满足居民,特别是低收入居民生活用电的基本需求,且不能引起居民太大的抵触情绪。在引导居民合理用电的前提下,尽量不牺牲他们用电的舒适度。其次,要考虑到社会因素,阶梯电价方案要能够提高经济效率,促进节能环保,促进社会公平正义,加速和谐社会的推进等等。最后,还需考虑供电企业的生存发展空间,使得供电企业有足够的资金良性发展。
本文从这三个评价准则方面各选取了3个具有典型意义的评价指标,根据模糊层次分析法原理,建立一个评价体系,将其分为目标层,准则层和指标层。如图1所示。
2.2. 阶梯电价评价指标计算
当前文献中对于指标的计算方法,多用专家打分法。这种方法具有很强的主观性,而且难以完成实际工程应用。本文针对这一缺陷提出了一种改进计算方法。利用线性支出原理等经济学原理,结合阶梯电价实行地区现有的用电数据,得出每个指标的计算公式。用实际的数据来代替主观的专家打分,从而使得评价更加客观和合理。

Figure 1. The hierarchical model structure of evaluation index system for tiered electricity pricing
图1. 阶梯电价方案评价层次模型结构图
由于评价指标用实际数据算出的数值会出现数量级不一,我们引入模糊层次分析法中综合评价的概念,利用相对隶属度值来统一各评价指标的数值。本文中,利用相对隶属度值,将各评价指标计算数值统一在60到100之间,并且数值越大评价越高。最后得到一个指标值集 。
。
2.2.1. 居民承受能力
居民阶梯电价很重要的一个指标就是保证收入低的居民能够承受实行后的阶梯电价,根据线性支出原理,本文收入低的居民电力价格弹性的量化形式如下
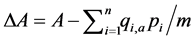 (1)
(1)
式中 ——低收入的居民在第i个用电阶梯的用电量;
——低收入的居民在第i个用电阶梯的用电量;
pi——第i个用电阶梯对应的电价;
 ——低收入居民每月的平均用电支出;
——低收入居民每月的平均用电支出;
m——低收入居民每户的月平均收入;
n——阶梯电价分为n个用电阶梯;
A——低收入居民的电费承受指数(A = 电费的支出/实际收入)。
若 是正数,则表示此方案考虑了低收入居民的承受能力,则给此方案加分;若其为负数,则需要扣分。
是正数,则表示此方案考虑了低收入居民的承受能力,则给此方案加分;若其为负数,则需要扣分。
在最极端情况下,即居民无电费负担时,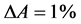 ,此时本项指标评价数值为100,利用相对隶属度值
,此时本项指标评价数值为100,利用相对隶属度值 ,得到这项指标的评价值计算公式为
,得到这项指标的评价值计算公式为
 (2)
(2)
2.2.2. 居民舒适度
阶梯电价第一档的电价一般与现行电价相同,若消费电量在此档电量以内的将不必为了实行阶梯电价而改变用电习惯。本项指标考虑的是满足居民舒适度的范围,即第一档居民的覆盖率。根据我国的综合国情考虑,阶梯电价第一档需要覆盖80%的居民[7] 。
在基准分80分的基础上,如果覆盖100%的居民,此时本项指标评价数值为100,利用相对隶属度值 ,得到这项指标的评价值计算公式为
,得到这项指标的评价值计算公式为
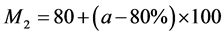 (3)
(3)
其中a为此方案第一档电量覆盖用户率。
2.2.3. 节电意识的培养
根据价格需求曲线可以知道,当价格高到一定程度的时候,居民用电的需求是一定的,这个数值即为基本用电需求。这个基本用电量不随价格的变动而变化,即价格弹性几乎为0。我国的阶梯电价第一阶梯电价不高于之前的电价,所以用电在第一阶梯电价内的居民不会感受到电价的变化。阶梯电价不会让这部分人产生节电意识。该人数百分比为前2.2.2中的a。
又因为对于高于平均居民消费量100%的人来说,他们的电费占支出的比例比较小,所以即使电价变高,他们也不会节约用电。这部分人数百分比为b,则节电意识影响的人群百分比为 。
。
根据统计数据, 一般不大于20%,我们设当其为20%时本项指标评价数值为100,则利用相对隶属度值
一般不大于20%,我们设当其为20%时本项指标评价数值为100,则利用相对隶属度值 ,得到这项指标的评价值计算公式为
,得到这项指标的评价值计算公式为
 (4)
(4)
2.2.4. 节能效果评价
在节能效果的方面,采用了线性支出系统模型,在有预算约束的条件下最大化后得出的方程式为
 (5)
(5)
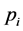 ——居民在第i个阶梯用电的价格;
——居民在第i个阶梯用电的价格;
 ——居民在第i个阶梯用电的需求量;
——居民在第i个阶梯用电的需求量;
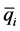 ——居民在第i个阶梯用电的基本需求量;
——居民在第i个阶梯用电的基本需求量;
 ——居民的月基本生活支出;
——居民的月基本生活支出;
 ——第i个阶梯用电的边际预算份额(除去基本消费需求的支出之外,将剩余的支出分配到第i个阶梯需求的比例);
——第i个阶梯用电的边际预算份额(除去基本消费需求的支出之外,将剩余的支出分配到第i个阶梯需求的比例);
 ——总消费支出。
——总消费支出。
如果居民阶梯电价分为n个阶梯,那么每户居民的月平均用电总量可表示为
 (6)
(6)
根据式(6)计算出实行阶梯电价前和实行阶梯电价后每户家庭月平均用的总电量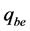 和
和 ,可以得到用电量之差
,可以得到用电量之差
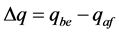 (7)
(7)
根据统计数据,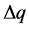 一般不会超过10度。我们设定当其为10度时,本项指标评价数值为100,则利用相对隶属度值
一般不会超过10度。我们设定当其为10度时,本项指标评价数值为100,则利用相对隶属度值 ,得到这项指标的评价值计算公式为
,得到这项指标的评价值计算公式为
 (8)
(8)
2.2.5. 对CPI的影响
假设居住类的权重为13%,而水电占其权重为40.8%,其中用电又占水电的权重为33.3% [8] 。假设除电力价格外,其他产品的价格不变,可以得到
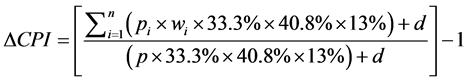 (9)
(9)
其中wi——第i个用电阶梯的权重系数;
d——本月其它产品价格和权重的乘积;
p——实行阶梯电价前的电价;
 ——居民购买的第i个用电阶梯的价格。
——居民购买的第i个用电阶梯的价格。
根据统计数据, 一般不会超过0.1%。设定
一般不会超过0.1%。设定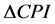 为0.1%时,本项指标评价数值为100,利用相对隶属度值
为0.1%时,本项指标评价数值为100,利用相对隶属度值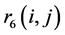 ,得到这项指标的评价值计算公式为
,得到这项指标的评价值计算公式为
 (10)
(10)
2.2.6. 供电公司利润
假设某地区用电户数有N个,按照家庭年收入将某地区城乡居民划分为s个等级,每个等级所占比率为rs,由公式(3)-(5)变化可以得到如下公式
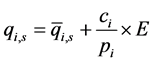 (11)
(11)
式中E——平均电费消费预算;
 ——第s个等级的用户在第i个阶梯用电的需求量;
——第s个等级的用户在第i个阶梯用电的需求量;
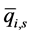 ——第s个等级的用户购买第i个阶梯用电的基本需求量(即满足消费者的基本需求量)这里修正
——第s个等级的用户购买第i个阶梯用电的基本需求量(即满足消费者的基本需求量)这里修正 系数,分别取0,0.1,0.01。
系数,分别取0,0.1,0.01。
我们可以得到实施阶梯电价后供电企业的售电收益的变化为
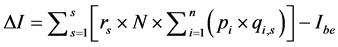 (12)
(12)
电网从发电企业中购买的成本相应会改变,首先是电量的改变,为
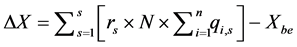 (13)
(13)
 为实施前购买电量,加上线路上的电损,可计算实施阶梯电价前后购买电量差为
为实施前购买电量,加上线路上的电损,可计算实施阶梯电价前后购买电量差为
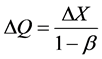 (14)
(14)
其中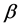 为配电网损。则成本差为
为配电网损。则成本差为
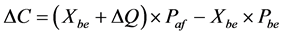 (15)
(15)
其中 分别是发电企业上网电价调整后与调整前的电价水平。
分别是发电企业上网电价调整后与调整前的电价水平。
可得供电利润为
 (16)
(16)
从而得到利润改变率为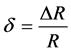 。根据统计数据,
。根据统计数据,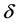 一般在20%到80%之间。我们设80%,此时本项指标评价数值为100,利用相对隶属度值
一般在20%到80%之间。我们设80%,此时本项指标评价数值为100,利用相对隶属度值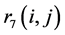 ,得到这项指标的评价值计算公式为
,得到这项指标的评价值计算公式为
 (17)
(17)
2.2.7. 电价上涨空间
这项指标评价电价在现有的基础上升高的能力。现阶段我国居民电价依然偏低,我国居民电价是低于工商业电价的,大约是其90%,而在国外一些发达国家,居民电价平均是工商业电价的150%。除此之外,居民电价上涨速度明显比较慢,低于其他资源价格的增速。
居民电费支出占其收入的比例可作为衡量此项指标的量化数据。根据我国现在的国情,电费支出占居民收入比例 在5%内比较好。对于供电公司来说,上涨空间小比较符合供电公司利益。
在5%内比较好。对于供电公司来说,上涨空间小比较符合供电公司利益。
当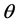 为5%时,本项指标评价数值为100,利用相对隶属度值
为5%时,本项指标评价数值为100,利用相对隶属度值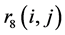 ,得到这项指标的评价值计算公式为
,得到这项指标的评价值计算公式为
 (18)
(18)
2.2.8. 智能计量设施投资成本回收速度
要实行阶梯电价,需要更换智能电表等智能计量设施,我们仅考虑最主要的支出,即智能电表更换产生的费用。该投资成本T的计算公式为
 (19)
(19)
其中:N为样本地区的用电户数,G为智能电表的价格。
供电公司的收益可以由式(12)得到
 (20)
(20)
根据统计数据可知智能计量设施的成本大约为10年到20年的收益,我们设10年收益可以完成投资时,本项指标评价数值为100,则利用相对隶属度值 ,得到这项指标的评价值计算公式为
,得到这项指标的评价值计算公式为
 (21)
(21)
2.2.9. 社会福利
社会福利变化是指就社会整体(本文指一般消费者和供电公司)而言,每个个体的平均收益。计算消费者的收益和供电公司的收益,再相加得到福利值。消费者收益为用阶梯电价代替目前电价后,消费者每月可以节约的费用,生产者收益为将现行电价变为阶梯电价后,供电公司可能产生的盈利。
即消费者收益为
 (22)
(22)
式中: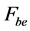 ——原来需要花费的电费。
——原来需要花费的电费。
供电公司收益为其增长的利润除以本地区的用电户数,增加利润为式(16)中的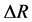 ,户数记为N,则供电公司福利计算公式为
,户数记为N,则供电公司福利计算公式为
 (23)
(23)
则社会福利变化为
 (24)
(24)
根据统计数据,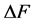 一般在0到3之间,设
一般在0到3之间,设 为3时,本项指标评价数值为100,利用相对隶属度值
为3时,本项指标评价数值为100,利用相对隶属度值 ,得到这项指标的评价值计算公式为
,得到这项指标的评价值计算公式为
 (25)
(25)
3. 构建基于模糊层次分析法的评价
3.1. 层次分析法的一般步骤
1) 构造判断矩阵及其标度。采用两两比较法将因素之间的相对重要性按一定标度定量化,并将其标度值排成方阵,构成了判断矩阵P。
2) 层次排序及其一致性检验。层次排序的过程也就是求解指标体系某层相应因素对于上一层某因素相对权值的过程。
3.2. 阶梯电价综合评价指标体系权值的确定
在第一步建立了系统层次模型后,上下层次之间的隶属关系就随之确定了,接下来就是要构造各层次元素的模糊判断矩阵。本文因素间的两两对比,引入九分位相对重要比例标度,构成判断矩阵A。矩阵A各元素Aij表示横行指标Ai对各列指标Aj的相对重要程度的两两比较值[9] 。
而由于A是一个正互反矩阵,每次判断时,只需要作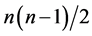 次比较即可。
次比较即可。
3.3. 权重向量W的计算
权重向量W的计算方法有很多种,比如几何平均法,算术平均法,特征向量法,最小二乘法[10] 。本文使用几何平均法来计算,具体计算方法如下
 (26)
(26)
 (27)
(27)
将Wi归一化得:
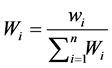 (28)
(28)
即各指标的权重系数值。
判断矩阵标度值用专家调查法获得,具体标度值如图1中各数值所示。
根据上文的权重计算方法,计算准则层权重值。准则层包含三个因素子集:B1,B2,B3。根据图1中所给的标度值,其判断矩阵为
 (29)
(29)
由此可以得到权重系数矩阵
 (30)
(30)
对其进行一致性检测:当 ,则判断矩阵具有一致性,说明以W各个分量作为相应各个因素的权值分配是合理的。
,则判断矩阵具有一致性,说明以W各个分量作为相应各个因素的权值分配是合理的。
同理,C层上的因素分别属于B1,B2,B3,根据图1给出的标度值,分别给出判断矩阵C1,C2,C3,本文中判断矩阵均取得满意的一致性。
 (31)
(31)
 (32)
(32)
 (33)
(33)
分别得到W1,W2,W3为
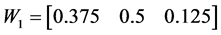 (34)
(34)
 (35)
(35)
 (36)
(36)
根据式(30),(34),(35)和(36),则可以得到本文的权重集为

权重值和相对应评价指标的评价值相乘后求和,得到最终的模糊评价综合指标:
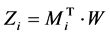 (37)
(37)
根据各个方案的 给出评语等级如表1。
给出评语等级如表1。
4. 实例分析
N市有A,B,C三种阶梯电价方案选择,如表2。
4.1. 各项指标计算
1) 居民承受能力
设低收入居民电费承受指数为A = 1%,由统计资料可知,N市低收入居民每户的月平均用电总量为150kW·h,则三种方案总的月平均用电支出为
A方案: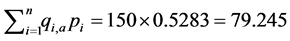
B方案:
C方案:
对收入居民每户的月平均收入m = 10,000 (元),则 。根据式(2),这三种方案本指标的评价值为
。根据式(2),这三种方案本指标的评价值为
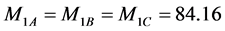 (38)
(38)
2) 居民舒适度
由统计资料可知N市居民用电量在180度以内的户数占总户数的78%,在204度以内的为85%,在230度以内的为93%。
根据式(3),可以得到这三种方案本指标的评价值为
 (39)
(39)
3) 节电意识的培养
由统计资料可知N市用电量高于平均居民用电量100%的用户数占总用户数的比例为5%,即b = 5%。
Table 1. Comment grade
表1. 评语等级
Table 2. Three schemes of tiered electricity pricing
表2. 三种阶梯电价方案
根据式(4),可以得到这三种方案本指标的评价值为
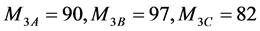 (40)
(40)
4) 节能效果评价
由统计资料可知,平均每户家庭的月基本用电量为180度,则 ,平均每户家庭的月总支出为6275,平均每户家庭的月基本生活支出为3097,则
,平均每户家庭的月总支出为6275,平均每户家庭的月基本生活支出为3097,则 。取
。取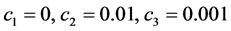 。根据
。根据 。实行阶梯电价前 取0.5283,实行后则按照各方案各阶梯电价来取值。则我们可以算出不实行阶梯电价时的用电量为
。实行阶梯电价前 取0.5283,实行后则按照各方案各阶梯电价来取值。则我们可以算出不实行阶梯电价时的用电量为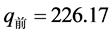 。则施行三种阶梯电价后的用电量分别为:
。则施行三种阶梯电价后的用电量分别为: ,
, ,
,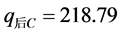 。由此可以得到
。由此可以得到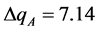 ,
, ,
,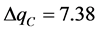 。
。
根据式(8),这三种方案本指标的评价值为
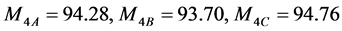 (41)
(41)
5) 对CPI的影响
对于N市,通过相关统计数据可以得到: ,
,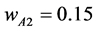 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, 。带入下式
。带入下式 ,可以得到A,B,C三种方案的CPI变化。根据式(10),可以得到三种方案本指标评价值为
,可以得到A,B,C三种方案的CPI变化。根据式(10),可以得到三种方案本指标评价值为
 (42)
(42)
6) 供电公司利润
本市具有231万户居民,具体情况见表3。
根据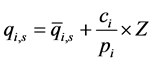 ,其中E为平均电费消费预算,
,其中E为平均电费消费预算, 为第s个等级消费者购买第i个阶梯用电的基本需求量(即满足消费者的基本需求量)这里修正
为第s个等级消费者购买第i个阶梯用电的基本需求量(即满足消费者的基本需求量)这里修正 系数,分别取0,0.1,0.01。三种方案施行后的情况,见表4。
系数,分别取0,0.1,0.01。三种方案施行后的情况,见表4。
则可以算出原来售电总额 ,原来的用电量为60,614万kWh。
,原来的用电量为60,614万kWh。
又根据式(12),可以得到三种方案收入变化为
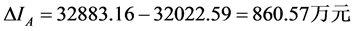


根据式(13),电量的变化为
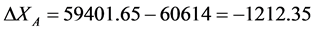


Table 3. Residents’ basic situation
表3. 居民基本情况
Table 4. Implementation of the scheme
表4. 各方案实施后情况
配电网损一般为3%,上网电价为0.47元/kWh,又根据(14),(15)得到成本变化为: ,
, ,
, ,
,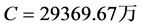 。又根据式(16),得到
。又根据式(16),得到 ,
, ,
,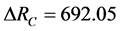 ,
, ,根据式(17),本项指标三种方案评价值分别为
,根据式(17),本项指标三种方案评价值分别为
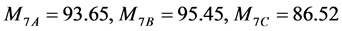 (43)
(43)
7) 电价上涨空间
根据统计资料可知N市中居民每户平均每月用电为220度,电费 ,则三种方案下其电费分别为:
,则三种方案下其电费分别为: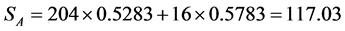 ,
,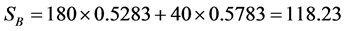 ,
, 。居民每户月平均收入为8000元。则三种方案电费占收入比分别为:
。居民每户月平均收入为8000元。则三种方案电费占收入比分别为: ,
, ,
,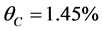 ,根据式(18)得到本指标三种方案评价值为
,根据式(18)得到本指标三种方案评价值为
 (44)
(44)
8) 智能计量设施投资成本
需要更换的电能表约花费200元,231万户共需要260万只表(有10%轮换裕度),根据式(19),得到T = 52,000万元。由上文可知供电公司利润为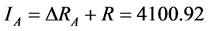 ,
,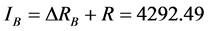 ,
, 。三种方案下的负担不同,根据式(21)得到本指标三种方案评价值为
。三种方案下的负担不同,根据式(21)得到本指标三种方案评价值为
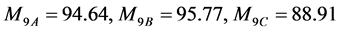 (45)
(45)
9) 社会福利计算
根据图1,和式(22),消费者福利为: ,
,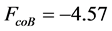 ,
, 。又根据式(23),可知
。又根据式(23),可知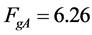 ,
, ,
, 。根据式(24),
。根据式(24), ,
, ,
,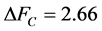 。根据式(25),可以得到本项的评价值为
。根据式(25),可以得到本项的评价值为
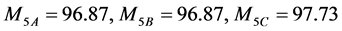 (46)
(46)
4.2. 综合评分
根据上文已经给出的模糊层次分析法权重集:
 ,再和对应评价指标的评价值集
,再和对应评价指标的评价值集 相乘,得到最终的模糊评价综合指标
相乘,得到最终的模糊评价综合指标 :
: ,
, ,
, 。
。
由此我们可以看出,三种方案在评分上相差不大。其中,方案C在总分上最高,说明综合评价中,方案C最优。在本文的评价体系中,节能减排权重占的比例比较大,所以方案C在这方面比较有优势,具体体现在居民舒适度,节能效果,社会福利三个方面相对其他两个方案有优势。
5. 结论
本文着重从指标计算和模糊层次分析法两个方面来进行评价体系设计。根据阶梯电价的实施目的,筛选出了阶梯电价方案评价关键指标,给出量化计算方法,利用相对隶属度值,统一指标值的数量级和大小;利用模糊层次分析法,对指标的权重进行计算。利用每个指标的权重值和对应模糊评价指标值相乘并求和,得到各方案的最终综合评价值,该分值反映了各方案预计实施效果,可以为阶梯电价方案的科学决策提供参考依据。
与现有文献的阶梯电价方案评估不同,本文提出的阶梯电价方案评价指标体系的特点主要体现在:
1) 本文对指标的计算是通过数学模型建立的函数,计算具有客观性和可操作性,能够根据统计数据体现不同地区的不同特点。
2) 本文采用模糊层次分析法对阶梯电价各个指标的权重进行了综合评价,综合考虑了各方面的因素,体现了评价的全面性,可以在多个指标中进行权衡,科学决策,选出一个较为合理的实行方案。
基金项目
江苏省高校自然科学基金(13KJB470010)。
文章引用
胡 骏,李天然,钱旭盛,应 亮,赵彩虹. 基于模糊层次分析法的阶梯电价方案评价
Evaluation of Tiered Electricity Pricing Schemes Based on Fuzzy Analytic Hierarchy Process[J]. 电气工程, 2016, 04(01): 11-22. http://dx.doi.org/10.12677/JEE.2016.41003
参考文献 (References)
- 1. 李红, 杜新伟. 四川居民阶梯电价效果分析及评价体系研究[J]. 四川电力技术, 2013, 36(6): 59-60.
- 2. 朱柯丁, 宋艺航, 谭忠富, 吴海林. 居民生活阶梯电价设计优化模型[J]. 华东电力, 2011, 39(6): 0863-0864.
- 3. 曾鸣, 吴建宏, 刘超, 王涛. 考虑多元因素的居民阶梯电价评估[J]. 华东电力, 2012, 40(3): 60-61.
- 4. 吴建宏. 基于社会均衡的居民阶梯电价定价模型及政策模拟研究[D]: [博士学位论文]. 北京: 华北电力大学, 2013.
- 5. 刘卓昶, 蔡金. 从管理经济学角度分析阶梯电价制定策略及其效益[J]. 华东电力, 2013, 24(10): 2159-2164.
- 6. 宋艺航. 我国居民生活用电阶梯电价设计优化模型[D]: [硕士学位论文]. 北京: 华北电力大学, 2011.
- 7. 国家发展和改革委员会. 关于居民生活用电试行阶梯电价的指导意见[EB/OL]. http://www.gov.cn/gzdt/2011-12/01/content_2007657.htm, 2011.
- 8. 曾鸣, 王致杰, 薛松, 刘珊珊. 基于效用理论的新电价政策对供电企业经济效益影响评估[J]. 电力经济研究, 2013, 11(11): 62-65.
- 9. 田玲. 基于层次分析法的购电方案模糊综合评价探讨[J]. 电网技术, 2005, 4(7): 25-26.
- 10. Zhao, X.L., Liu, X.J. and Xiao, C.Y. (2010) Application of Optimal Membership Degree in Optimizing Well Completion Based on Fuzzy Analytic Hierarchy Process. 2010 Second WRI Global Congress on Intelligent Systems (GCIS), Wuhan, 16-17 December 2010, 191-194. http://dx.doi.org/10.1109/GCIS.2010.15
