Pure Mathematics
Vol.06 No.01(2016), Article ID:16793,6
pages
10.12677/PM.2016.61003
On Quasiprimitive Permutation Groups of Cube-Free Degree
Shiqin Peng1, Xiaofen Yu2, Jiangmin Pan1*
1College of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming Yunnan
2School of Mathematics and Information Science, Neijiang Normal University, Neijiang Sichuan

Received: Dec. 14th, 2015; accepted: Jan. 17th, 2016; published: Jan. 21st, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Li and Seress [The primitive permutation groups of square-free degree, BULL. London Math. Soc. 35 (2003), 635-644] classified primitive permutation groups of square-free degree. In this paper, we will characterize quasiprimitive permutation groups of cube-free degree, and give several problems worth further research.
Keywords:Quasiprimitive Permutation Group, O’Nan-Scott Theorem, Simple Group

立方自由次拟本原置换群
彭仕芹1,余小芬2,潘江敏1*
1云南财经大学统计与数学学院,云南 昆明
2内江师范学院数学与信息科学学院,四川 内江

收稿日期:2015年12月14日;录用日期:2016年1月17日;发布日期:2016年1月21日

摘 要
Li和Seress [The primitive permutation groups of square-free degree, BULL. London Math. Soc. 35 (2003), 635-644]分类了平方自由次本原置换群。本文我们将给出立方自由次拟本原置换群的刻画,并提出几个关联的、有待进一步研究的问题。
关键词 :拟本原置换群,O’Nan-Scott定理,单群

1. 介绍
设 为集合
为集合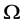 上的一个传递置换群,
上的一个传递置换群, 称为
称为 的次数。
的次数。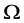 的一个非空子集
的一个非空子集 称为
称为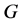 在
在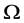 上的一个块(或区组),如果对任意
上的一个块(或区组),如果对任意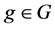 都有
都有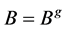 或者
或者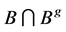 为空集。此时,称
为空集。此时,称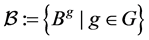 为
为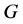 在
在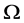 上的一个块系统。显然,单点集和
上的一个块系统。显然,单点集和 都是
都是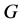 的块,称为
的块,称为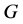 的平凡块。群
的平凡块。群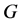 称为
称为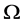 上的本原置换群如果
上的本原置换群如果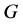 在
在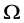 上没有其余的(非平凡)块,或者等价地,
上没有其余的(非平凡)块,或者等价地,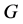 在
在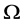 上的点稳定子群
上的点稳定子群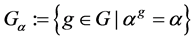 为
为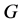 的极大子群,其中
的极大子群,其中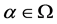 。群
。群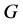 称为
称为 上的拟本原置换群如果
上的拟本原置换群如果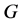 的每个极小正规子群在
的每个极小正规子群在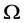 上都是传递的。容易证明:本原置换群一定是拟本原的,反之,则不然。
上都是传递的。容易证明:本原置换群一定是拟本原的,反之,则不然。
刻画本原置换群有着十分悠久和丰富的历史。1900年,著名代数学家Burnside完全确定了所有素数次的传递置换群(显然这些群是本原的),并提出了刻画更多本原置换群类的问题。事实上,由于任何一个传递置换群都可以诱导一个其块系统上的本原置换群,本原置换群的研究是置换群研究的根本问题之一。Wielandt (1949年)刻画了包含一个传递二面体子群的本原置换群;Scott (1961年)确定了包含一个同构于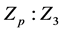 (其中
(其中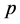 为素数)的亚循环传递子群的本原置换群;Praeger ([1] )刻画了本原置换群的嵌入问题;华裔代数组合学家Li (2003年)解决了Burnside的百年公开问题:包含一个交换传递子群的本原置换群的分类(见 [2] )。近期,Li和Pan ( [3] )分类了包含一个传递亚循环子群的本原置换群。基于拟本原置换群是本原置换群的推广,并且在多个领域(尤其在代数组合领域)有着十分重要的应用,拟本原置换群的研究也受到了学者们的极大关注;Praeger ([4] )推广了本原置换群的O’Nan-Scott定理,将拟本原置换群分成了八种类型;Li ( [5] )确定了包含传递二面体子群的拟本原置换群。
为素数)的亚循环传递子群的本原置换群;Praeger ([1] )刻画了本原置换群的嵌入问题;华裔代数组合学家Li (2003年)解决了Burnside的百年公开问题:包含一个交换传递子群的本原置换群的分类(见 [2] )。近期,Li和Pan ( [3] )分类了包含一个传递亚循环子群的本原置换群。基于拟本原置换群是本原置换群的推广,并且在多个领域(尤其在代数组合领域)有着十分重要的应用,拟本原置换群的研究也受到了学者们的极大关注;Praeger ([4] )推广了本原置换群的O’Nan-Scott定理,将拟本原置换群分成了八种类型;Li ( [5] )确定了包含传递二面体子群的拟本原置换群。
一个正整数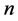 称为平方自由的,如果不存在素数
称为平方自由的,如果不存在素数 使得
使得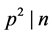 ;
;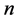 称为立方自由的,如果不存在素数
称为立方自由的,如果不存在素数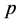 使得
使得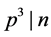 。Li和Seress ( [6] )证明了平方自由次本原置换群一定为仿射型或几乎单型,并给出了它们的完全分类。在本文中,我们将给出立方自由次拟本原置换群G的一个刻画:我们证明了G将出现在O’Nan-Scott定理的五种类型中,并确定了除几乎单型外的其余四种类型中的群G。
。Li和Seress ( [6] )证明了平方自由次本原置换群一定为仿射型或几乎单型,并给出了它们的完全分类。在本文中,我们将给出立方自由次拟本原置换群G的一个刻画:我们证明了G将出现在O’Nan-Scott定理的五种类型中,并确定了除几乎单型外的其余四种类型中的群G。
本文使用的符号都是标准的。例如,对一个正整数n,我们用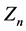 表示n阶循环群;对两个群N和H,用
表示n阶循环群;对两个群N和H,用 表示N与H的直积,用
表示N与H的直积,用 表示N和H的中心乘积,用
表示N和H的中心乘积,用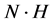 表示N被H的扩张,当这个扩张是可裂时,我们用
表示N被H的扩张,当这个扩张是可裂时,我们用 表示。
表示。
本文所得的主要结果是下面的定理,其中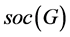 表示群
表示群 的柱心(即
的柱心(即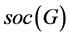 是
是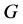 的所有极小正规子群的乘积)。显然,
的所有极小正规子群的乘积)。显然,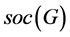 是
是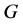 的特征子群。为方便起见,拟本原置换群的八种类型见第3节的介绍。
的特征子群。为方便起见,拟本原置换群的八种类型见第3节的介绍。
定理1.1 设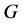 为集合
为集合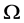 上的立方自由次拟本原置换群,
上的立方自由次拟本原置换群,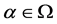 ,则
,则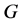 为几乎单群,或者下述之一成立:
为几乎单群,或者下述之一成立:
1)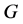 为HA型本原置换群,且下述之一成立:
为HA型本原置换群,且下述之一成立:
①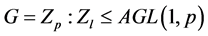 ,其中
,其中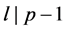 ;
;
②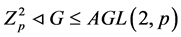 ,且
,且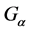 为
为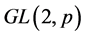 的不可约子群。
的不可约子群。
2)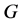 为HS型本原置换群,
为HS型本原置换群,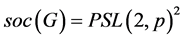 ,其中
,其中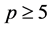 且
且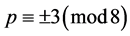 ,且
,且
 。
。
3)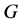 为SD型,
为SD型,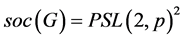 ,且
,且 ,其中
,其中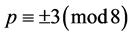 ,
,
 。
。
4)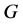 为PA型,且
为PA型,且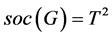 ,其中
,其中 为文 [6] 中表1~4中的非交换单群。
为文 [6] 中表1~4中的非交换单群。
本文的结构如下:我们将在第2节介绍一些预备知识,并证明几个引理;第3节将给出定理1.1的证明,并构造了几个具体的例子;第4节将提出几个有待进一步研究的问题。
2. 预备知识
设 为一个群,
为一个群,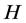 为
为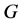 的子群,设
的子群,设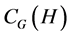 和
和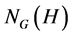 分别表示
分别表示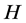 在
在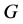 中的中心化子和正规化子。下的结论是著名的
中的中心化子和正规化子。下的结论是著名的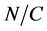 定理,见( [7] , CH. I. Lemma 4.5]。
定理,见( [7] , CH. I. Lemma 4.5]。
引理2.1 设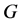 为一个群,
为一个群,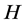 为
为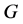 的子群,则
的子群,则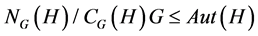 。
。
一个群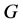 称为完全群,如果
称为完全群,如果 等于自身的换位子群
等于自身的换位子群 ;一个群扩张
;一个群扩张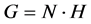 称为中心扩张,如果
称为中心扩张,如果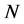 包含在
包含在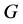 的中心
的中心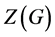 中。如果群
中。如果群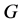 是一个完全群,且商群
是一个完全群,且商群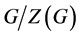 与一个单群
与一个单群 同构,则称
同构,则称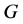 为
为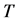 的一个覆盖群。Schur [8] 证明了任何一个单群(更一般的,完全群)
的一个覆盖群。Schur [8] 证明了任何一个单群(更一般的,完全群)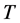 都有一个覆盖群
都有一个覆盖群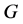 使得
使得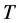 的每个覆盖群都是
的每个覆盖群都是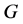 的同态像。此时,
的同态像。此时,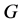 的中心
的中心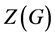 称为
称为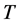 的Schur乘子(见 [9] , p. 43)。所有非交换单群的Schur乘子都是已知的(见 [9] , p. 302-303)。下面的引理见( [10] , Lemma 2.11)。
的Schur乘子(见 [9] , p. 43)。所有非交换单群的Schur乘子都是已知的(见 [9] , p. 302-303)。下面的引理见( [10] , Lemma 2.11)。
引理2.2 设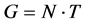 为
为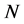 被
被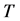 的扩张,其中
的扩张,其中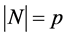 或
或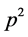 ,
,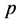 为素数,
为素数,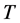 为非交换单群,则
为非交换单群,则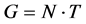 为中心扩张,
为中心扩张,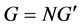 ,且
,且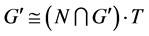 为完全群,其中
为完全群,其中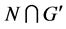 同构于
同构于 的Schur乘子的一个子群。
的Schur乘子的一个子群。
我们知道:本原置换群一定是拟本原的,但拟本原置换群不一定本原。下面的结论表明:对于包含一个传递交换子群的置换群而言,本原和拟本原是等价的。
引理2.3 包含交换传递子群的拟本原置换群是本原的。
证明:设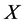 为集合
为集合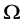 上的拟本原置换群且包含一个交换正则正规子群
上的拟本原置换群且包含一个交换正则正规子群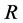 ,则
,则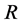 在
在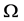 上正则。
上正则。
假设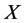 在
在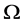 上非本原,则
上非本原,则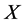 在
在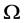 上有非平凡的块
上有非平凡的块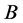 。设
。设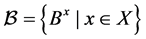 为
为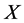 的相应的块系统,则
的相应的块系统,则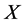 在
在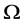 上的作用可自然诱导在
上的作用可自然诱导在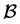 上的作用。显然,
上的作用。显然,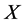 和
和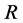 作用在
作用在 上都是传递的。设
上都是传递的。设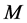 和
和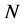 分别为
分别为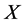 和
和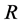 作用在
作用在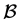 上的核,则
上的核,则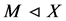 ,
,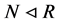 ,
,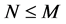 ,且
,且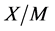 和
和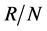 都是
都是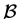 上的传递置换群。因为
上的传递置换群。因为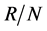 为交换群,所以
为交换群,所以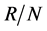 在
在 上正则,故
上正则,故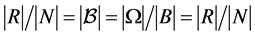 ,推出
,推出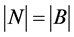 。注意到 在
。注意到 在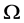 上正则,
上正则,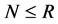 在
在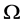 上半正则,我们得到
上半正则,我们得到 在
在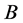 上正则,从而
上正则,从而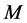 在
在 上传递,亦即:
上传递,亦即: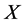 有一个非平凡的正规子群
有一个非平凡的正规子群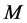 在
在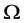 上不传递,这与
上不传递,这与 为
为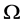 上的拟本原置换群矛盾。
上的拟本原置换群矛盾。
引理2.4 设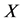 为立方自由阶群,则
为立方自由阶群,则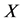 为可解群,或者
为可解群,或者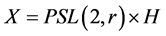 ,其中
,其中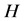 为
为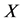 的奇数阶可解群,
的奇数阶可解群,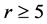 为素数使得:
为素数使得: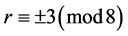 。
。
证明:首先,设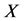 有不可解的极小正规子群
有不可解的极小正规子群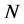 ,则
,则 ,其中
,其中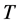 为非交换单群,
为非交换单群,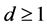 。因为
。因为 立方自由,且
立方自由,且 ,我们有
,我们有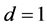 。进一步,由( [11] , Theorem p. 18)知
。进一步,由( [11] , Theorem p. 18)知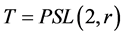 ,其中
,其中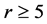 ,且
,且 。因为
。因为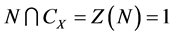 ,其中
,其中 表示
表示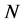 的中心,所以
的中心,所以 。进一步,因为
。进一步,因为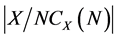 为奇数,由引理2.1,
为奇数,由引理2.1,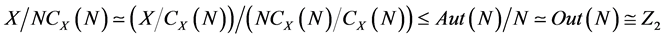 ,我们有
,我们有 ,且因为
,且因为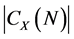 为奇数,
为奇数,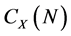 为可解群。
为可解群。
所以,要完成引理的证明,我们只需证明:当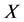 为不可解群时,
为不可解群时,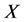 一定有不可解的极小正规子群。假设此断言不成立,设
一定有不可解的极小正规子群。假设此断言不成立,设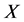 为极小阶反例。令
为极小阶反例。令 为
为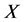 的一个极小正规子群,则
的一个极小正规子群,则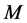 可解,故
可解,故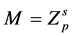 ,其中
,其中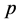 为素数,
为素数,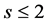 。因为
。因为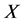 不可解,
不可解,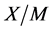 不可解,由关于
不可解,由关于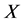 的极小性假设,
的极小性假设, 有不可解的极小正规子群,设为
有不可解的极小正规子群,设为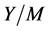 。由上面的讨论,有
。由上面的讨论,有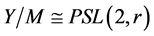 ,其中
,其中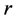 为素数使得
为素数使得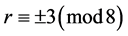 。因为
。因为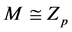 或
或 ,由引理2.2,
,由引理2.2,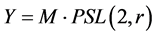 为中心扩张。进一步,因为
为中心扩张。进一步,因为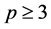 且
且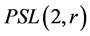 的Schur乘子为
的Schur乘子为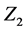 ,我们有
,我们有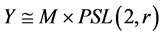 。特别地,
。特别地,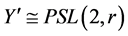 为
为 的一个不可解极小正规子群,矛盾。
的一个不可解极小正规子群,矛盾。
3. 定理1.1的证明
设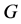 为集合
为集合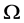 上的一个拟本原置换群,由[4] ,
上的一个拟本原置换群,由[4] ,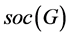 为
为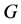 的一个极小正规子群,或者
的一个极小正规子群,或者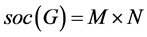 ,其中
,其中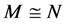 都是
都是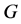 的非交换极小正规子群,且在
的非交换极小正规子群,且在 上正则。进一步,
上正则。进一步, 为以下八种类型之一,其中
为以下八种类型之一,其中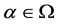 :
:
HA (仿射型):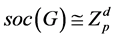 且
且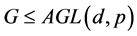 ,其中
,其中 为素数,
为素数, ;
;
HS (全形单型):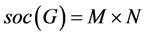 ,
,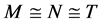 都为非交换单群且在
都为非交换单群且在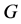 中正规在
中正规在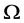 上正则,且
上正则,且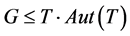 ;
;
HC (全形复合型):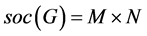 ,
,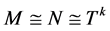 都为
都为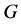 的极小正规子群且在
的极小正规子群且在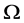 上正则,且
上正则,且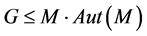 ,其中
,其中 ,
,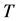 为非交换单群;
为非交换单群;
AS (几乎单型):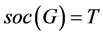 为非交换单群,且
为非交换单群,且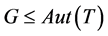 ;
;
TW (绕圈积型):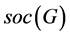 为
为 的一个非交换非单的极小正规子群,且在
的一个非交换非单的极小正规子群,且在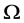 上正则;
上正则;
SD (单对角型):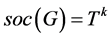 ,且
,且 ,其中
,其中 ,
,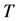 为非交换单群;
为非交换单群;
CD (复合对角型): ,且
,且 ,其中
,其中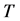 为非交换单群,
为非交换单群,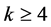 ,
,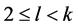 且
且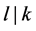 ;
;
PA (乘积作用型):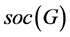 为
为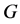 的非交换极小正规子群,且在
的非交换极小正规子群,且在 上不正则。
上不正则。
引理3.1 设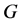 为集合
为集合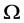 上的立方自由次拟本原置换群,则
上的立方自由次拟本原置换群,则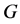 不是HC型,CD型和TW型。
不是HC型,CD型和TW型。
证明:假设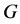 为HC型,则
为HC型,则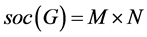 ,且
,且 在
在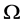 上正则,其中
上正则,其中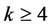 为偶数,故
为偶数,故 。因为
。因为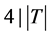 ,且
,且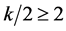 ,我们有
,我们有 ,这与
,这与 为立方自由矛盾。所以,
为立方自由矛盾。所以,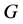 不是HC型。
不是HC型。
假设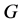 为CD型,则
为CD型,则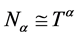 ,其中
,其中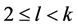 且
且 ,故
,故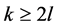 。因为
。因为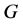 在
在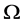 上拟本原,
上拟本原,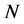 在
在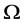 上传递,所以
上传递,所以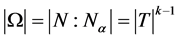 为
为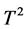 的倍数,从而为16的倍数,矛盾。
的倍数,从而为16的倍数,矛盾。
假设 为TW型,则
为TW型,则 在
在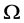 上正则,其中
上正则,其中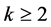 。此时,我们亦有
。此时,我们亦有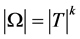 不是立方自由,矛盾。
不是立方自由,矛盾。
现在,我们给出定理1.1的证明。
设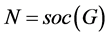 ,则
,则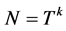 ,其中
,其中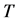 为单群,
为单群, 。
。
首先设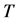 为交换群,则
为交换群,则 ,
,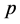 为素数,且
为素数,且 在
在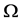 上正则,故
上正则,故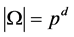 。因为
。因为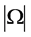 立方自由,我们有
立方自由,我们有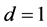 或2。若
或2。若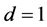 ,则
,则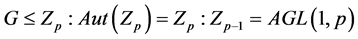 ,故
,故 ,其中
,其中 ·若
·若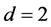 ,则
,则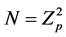 ,且
,且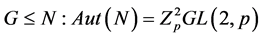 。由引理2.3,
。由引理2.3, 在
在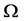 上本原,故
上本原,故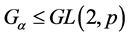 为
为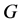 的极大子群,或者等价地,
的极大子群,或者等价地,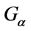 为
为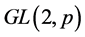 的不可约子群(即:
的不可约子群(即: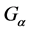 不正规化
不正规化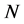 的任何非平凡子群)。
的任何非平凡子群)。
下设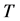 为非交换单群,且
为非交换单群,且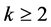 。由引理3.1,
。由引理3.1,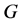 不是HC型,CD型和TW型。以下,我们分析其它几种型。
不是HC型,CD型和TW型。以下,我们分析其它几种型。
设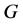 为HS型,则
为HS型,则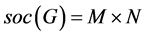 ,其中
,其中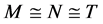 为
为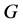 的正规子群且在
的正规子群且在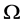 上正则。因为
上正则。因为 立方自由,由引理2.4,
立方自由,由引理2.4,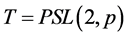 ,其中
,其中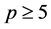 为素数,且
为素数,且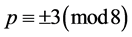 。因为
。因为 ,我们有
,我们有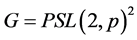 或
或 。此时,易知
。此时,易知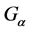 为
为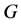 的极大子群,故
的极大子群,故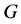 是本原的。
是本原的。
设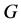 为SD型,则
为SD型,则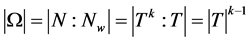 。因为
。因为 为立方自由数,我们有
为立方自由数,我们有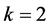 且
且 立方自由。故由引理2.4,
立方自由。故由引理2.4,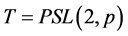 且
且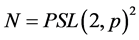 ,其中
,其中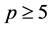 为素数且
为素数且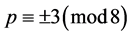 。进一步,
。进一步,
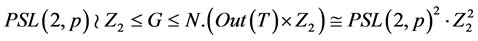 。
。
最后,假设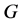 为PA型,则
为PA型,则 且
且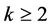 。设
。设 为
为 在
在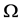 上的一个极大块系统,则
上的一个极大块系统,则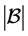 整除
整除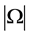 ,且
,且 为PA型本原置换群。因为
为PA型本原置换群。因为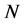 为
为 的唯一极小正规子群,
的唯一极小正规子群,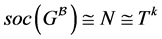 ,故存在正整数
,故存在正整数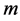 使得
使得 ,因为
,因为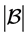 立方自由,我们有
立方自由,我们有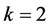 。现在,设
。现在,设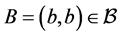 ,则
,则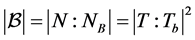 立方自由,所以
立方自由,所以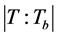 平方自由,故
平方自由,故 为文 [6] 中表1~4中的非交换单群。
为文 [6] 中表1~4中的非交换单群。
设 为一个群,
为一个群,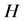 为
为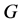 的一个子群,
的一个子群,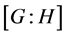 表示
表示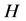 在
在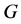 中全体右陪集构成的集合。则
中全体右陪集构成的集合。则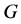 可以如下作用在
可以如下作用在 上:
上:
 ,
,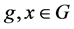 。
。
这个作用称为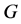 在
在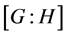 上的陪集作用。容易证明:这个陪集作用是忠实的当且仅当
上的陪集作用。容易证明:这个陪集作用是忠实的当且仅当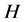 在
在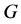 中柱心单(即:
中柱心单(即: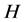 不包含
不包含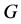 的任何非平凡正规子群):此时,
的任何非平凡正规子群):此时,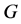 可视为集合
可视为集合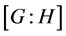 上的传递置换群。一个众所周知的结果是:
上的传递置换群。一个众所周知的结果是: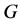 在集合
在集合 上的一个传递作用等价于
上的一个传递作用等价于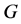 在
在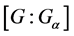 上的陪集作用,其中
上的陪集作用,其中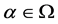 。
。
HA型立方自由次的拟本原置换群已由定理1.1 1)完全给出。下面,我们构造HS,SD和PA型立方自由次拟本原置换群的几个具体的例子(我们略去它们不困难的证明)。
例1 设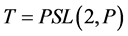 ,其中
,其中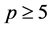 为素数使得
为素数使得 立方自由。设
立方自由。设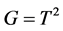 ,则
,则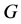 恰有两个极小正规子群。设
恰有两个极小正规子群。设 ,则
,则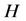 为
为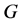 的极大子群。
的极大子群。
设 ,
,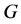 陪集作用在
陪集作用在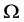 ,则
,则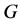 为
为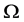 上
上 次(立方自由) HS型本原置换群。
次(立方自由) HS型本原置换群。
例2 设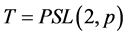 ,其中
,其中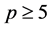 为素数使得
为素数使得 立方自由。设
立方自由。设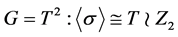 ,则
,则 有唯一的极小正规子群
有唯一的极小正规子群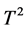 ;设
;设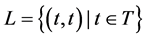 ,则
,则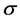 中心化
中心化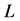 。令
。令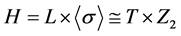 。
。
设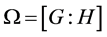 ,
, 陪集作用在
陪集作用在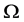 ,则
,则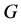 为
为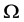 上
上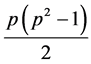 次(立方自由) SD型本原置换群。
次(立方自由) SD型本原置换群。
例3 设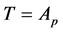 为交错单群,其中
为交错单群,其中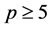 为素数。设
为素数。设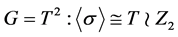 。
。
1) 设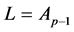 为
为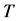 的子群,
的子群,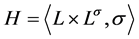 ,则
,则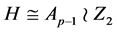 。设
。设 ,
,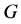 陪集作用在
陪集作用在 上,则
上,则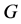 为
为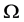 上
上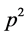 次PA型本原置换群。
次PA型本原置换群。
2) 进一步假设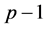 平方自由,设
平方自由,设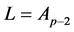 为
为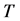 的子群,
的子群,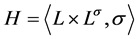 ,则
,则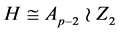 。设
。设 ,
,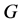 陪集作用在
陪集作用在 ,则
,则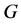 为
为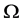 上
上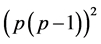 次位方自由) PA型拟本原(但非本原)置换群。
次位方自由) PA型拟本原(但非本原)置换群。
4. 后续研究的问题
对于HA,HS,SD和PA型,定理1.1确定了相应的立方自由次拟本原置换群,但我们未能确定几乎单型的立方自由次拟本原置换群。由此,我们提出下面的问题(容易知道它等同于确定几乎单型的立方自由次拟本原置换群)。
问题1. 确定所有的非交换单群 和其子群
和其子群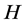 使得指数
使得指数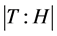 为立方自由。
为立方自由。
集合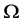 上的一个传递置换群
上的一个传递置换群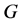 称为二部拟本原的,如果
称为二部拟本原的,如果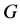 的每个非平凡正规子群在
的每个非平凡正规子群在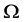 上最多有两个轨道,并且
上最多有两个轨道,并且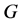 至少有一个非平凡的正规子群在
至少有一个非平凡的正规子群在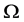 上恰有两个轨道。二部拟本原置换群是拟本原置换群的推广。基于二部拟本原置换群在一些领域的重要应用,研究下面的问题是自然且有意义的。
上恰有两个轨道。二部拟本原置换群是拟本原置换群的推广。基于二部拟本原置换群在一些领域的重要应用,研究下面的问题是自然且有意义的。
问题2. 刻画立方自由次的二部拟本原置换群。
最后,我们给出本文所研究问题以及上述问题1和2在代数图论中的一个关联的、值得研究的问题(事实上,它也是本文的一个研究动机之一)。
设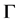 为一个图,
为一个图,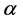 为
为 的一个顶点,
的一个顶点, 为
为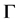 中所有与
中所有与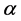 邻接的顶点构成的集合(称为
邻接的顶点构成的集合(称为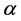 在
在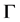 中的邻域)。如果
中的邻域)。如果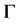 有一个自同构群
有一个自同构群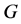 使得点稳定子群
使得点稳定子群 作用在
作用在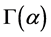 上是本原的,则称
上是本原的,则称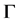 为
为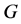 —局部本原图。局部本原图包含很多有趣的图类,是代数图论中重要的研究对象之一代数学家Praeger的著名结果告诉我们:任何一个局部本原图都是一个顶点拟本原或顶点二部拟本原局部本原图(称为基图)的正规覆盖(这个结果由 [4] 对2—弧传递图首先得到,并被 [12] 推广到局部本原图上)。
—局部本原图。局部本原图包含很多有趣的图类,是代数图论中重要的研究对象之一代数学家Praeger的著名结果告诉我们:任何一个局部本原图都是一个顶点拟本原或顶点二部拟本原局部本原图(称为基图)的正规覆盖(这个结果由 [4] 对2—弧传递图首先得到,并被 [12] 推广到局部本原图上)。
问题3. 刻画立方自由阶的局部本原基图。
基金项目
国家自然科学基金资助项目(11231008, 11461077)资助。
文章引用
彭仕芹,余小芬,潘江敏. 立方自由次拟本原置换群
On Quasiprimitive Permutation Groups of Cube-Free Degree[J]. 理论数学, 2016, 06(01): 17-22. http://dx.doi.org/10.12677/PM.2016.61003
参考文献 (References)
- 1. Praeger, C.E. (1990) The Inclusion Problem for Finite Primitive Permutation Group. Proceedings of the London Mathematical Society, 60, 68-88. http://dx.doi.org/10.1112/plms/s3-60.1.68
- 2. Li, C.H. (2003) The Finite Primitive Permutation Groups Containing an Abelian Regular Subgroup. Proceedings of the London Mathematical Society, 87, 725-748. http://dx.doi.org/10.1112/S0024611503014266
- 3. Li, C.H. and Pan, J.M. Primitive Permutation Groups Containing a Transitive Metacyclic Subgroup. Submitted.
- 4. Praeger, C.E. (1992) An O’Nan-Scott Theorem for Finite Quasiprimitive Permutation Groups and an Application to 2-Arc Transitive Graphs. Journal of the London Mathematical Society, 47, 227-239.
- 5. Li, C.H. (2006) Finite Edge-Transitive Cayley Graphs and Rotary Cayley Maps. Transactions of the American Mathematical Society, 358, 4605-4635. http://dx.doi.org/10.1090/S0002-9947-06-03900-6
- 6. Li, C.H. and Seress, A. (2003) The Primitive Permutation Groups of Square-Free Degree. Bulletin of the London Mathematical Society, 35, 635-644. http://dx.doi.org/10.1112/S0024609303002145
- 7. Huppert, B. (1967) Finite Groups. Springer-Verlag, Berlin.
- 8. Schur, I. (1907) Untersuchen über die Darstellung der endlichen Gruppen durch gebrochenen linearen Substitutionen. CreLLe J, 132, 85-137.
- 9. Gorenstein, D. (1982) Finite Simple Groups. Plenum Press, New York. http://dx.doi.org/10.1007/978-1-4684-8497-7
- 10. Pan, J.M., Liu, Y., Huang, Z.H. and Liu, C.L. (2014) Tetrava-lent Edge-Transitive Graphs of Order p2q. Science in China Series B, 57, 293-302. http://dx.doi.org/10.1007/s11425-013-4708-8
- 11. Gorenstein, D. (1980) Finite Groups. 2nd Edition, AMS Publishing, American.
- 12. Li, C.H. and Pan, J.M. (2007) Finite 2-Arc-Transitive Abelian Cayley Graphs. European Journal of Combinatorics, 29, 148-158. http://dx.doi.org/10.1016/j.ejc.2006.12.001
*通讯作者。