Pure Mathematics
Vol.06 No.03(2016), Article ID:17375,8
pages
10.12677/PM.2016.63021
Degree Based Topological Index Calculation of Pent-Heptagonal Nanotubes
Jing He, Wei Gao
School of Information, Yunnan Normal University, Kunming Yunnan

Received: Apr. 3rd, 2016; accepted: Apr. 18th, 2016; published: Apr. 21st, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Topological index is an available numerically way of the molecular structure, it can fully reflect the molecular graphs connection information and chemical environment, can effectively express the structure and properties of the compounds. In this paper, by means of edge set partitioning technique, we obtain several topological indices of Pent-Heptagonal nanotubes.
Keywords:Pent-Heptagonal Nanotube, Molecular Graph, Generalized Randić Index, Generalized Zagreb Index

Pent-Heptagonal纳米管基于度的拓扑指数计算
何静,高炜
云南师范大学信息学院,云南 昆明

收稿日期:2016年4月3日;录用日期:2016年4月18日;发布日期:2016年4月21日

摘 要
拓扑指数是分子结构数值化的一种方式,它能充分反映分子图的连接信息和化学环境,能有效地表达化合物的结构与性质。本文利用边集划分技术,得到Pent-Heptagonal纳米管若干基于度的拓扑指数。
关键词 :Pent-Heptagonal纳米管,分子图,广义Randić指数,广义Zagreb指数

1. 引言
在化学图论中,我们用一个图来描述分子的拓扑结构,用顶点表示原子,边表示化学键,该图称为分子图。拓扑指数是从化合物的结构图衍生出来的不变量。它不但可以定量的描述分子的结构,而且可以分析相关分子的结构与性能之间的关系。相关内容可参考 [1] - [12] 。
用 表示顶点/原子
表示顶点/原子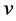 的度。分子图
的度。分子图 的拓扑指数是分子结构数值化的一种方式。1972年Trinajstić和Gutman引入了的第一Zagreb指数和第二Zagreb指数:
的拓扑指数是分子结构数值化的一种方式。1972年Trinajstić和Gutman引入了的第一Zagreb指数和第二Zagreb指数:
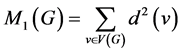 ,
,
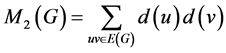 。
。
1975年,美国化学家Milan Randić [2] 提出了最古老的连通性指数,定义为
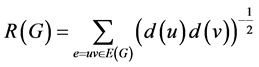
1988年,Bollobas和Erdos在 [6] 中推广了Randi指数,用任意实数k代替了,从而定义了广义的Randić指数:
 ,
,
其中k是非零实数。以下若没有特别说,k均表示非零实数。
当k = 1时,广义的Randić指数就是我们通常说的第二Zagreb指数。当k = −1时,广义的Randić指数就是修改的第二Zagreb指数。
Azari和Iranmanesh [13] 引入广义Zagreb指数,定义为
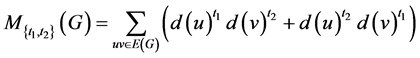 ,
,
其中 和
和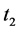 为任意的非负整数。
为任意的非负整数。
和连通指数则定义为:
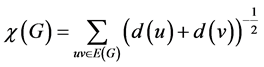
推广形式的和连通指数为
 。
。
而调和指数则定义为:
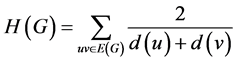
它的广义形式为:
 。
。
Eliasi和Iranmanesh [14] 定义广义几何代数指数如下:
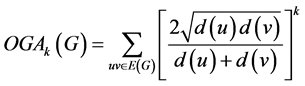 。
。
当k = 1时,即为一般GA指数如下:
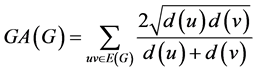 。
。
Estrada等人 [15] 定义原子键连通指数(atom-bound connectivity index,简称ABC指数)如下:
 。
。
两类Zagreb指数对应的多项式分别为
 ,
,
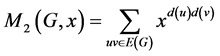 。
。
此外,第三类Zagreb指数和多项式定义为
 ,
,
 。
。
Gutman [16] 给出分子图的乘法Zagreb指数定义如下
 ,
,
 。
。
其中 为第一类乘法Zagreb指数,
为第一类乘法Zagreb指数, 为第二类乘法Zagreb指数。
为第二类乘法Zagreb指数。
Usha等人 [17] 重新定义了三类Zagreb指数如下:
 ,
,
 ,
,
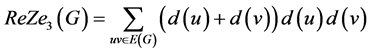 。
。
Furtula和Gutman [18] 定义了F指数如下:
 。
。
设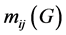 为满足
为满足 和
和 的边e = uv的个数,则M-多项式定义为
的边e = uv的个数,则M-多项式定义为
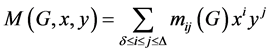 。
。
广义ABC指数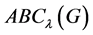 和and增强的Zagreb指数
和and增强的Zagreb指数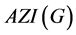 则定义为 [19] :
则定义为 [19] :
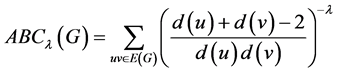 ,
,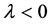
 。
。
最后,减弱的倒数Randić指数定义为
 。
。
第二减弱的倒数Randić指数定义为
 。
。
Pent-Heptagonal纳米管 是由周期长度为5的
是由周期长度为5的 (五边形)和周期长度为7的
(五边形)和周期长度为7的 (七边形)相互交替构成的网状化合物。设
(七边形)相互交替构成的网状化合物。设 纳米管的2维拉丁网格中,第一行和列的7边形个数分别为m和n (见图2)。将
纳米管的2维拉丁网格中,第一行和列的7边形个数分别为m和n (见图2)。将 纳米管记为
纳米管记为 。
。 纳米管的圆柱和2维拉丁网络可参考图1和图2。
纳米管的圆柱和2维拉丁网络可参考图1和图2。

Figure 1. Pent-Heptagonal Nanotubes cylindrical lattice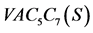
图1. Pent-Heptagonal纳米管的圆筒晶格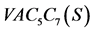
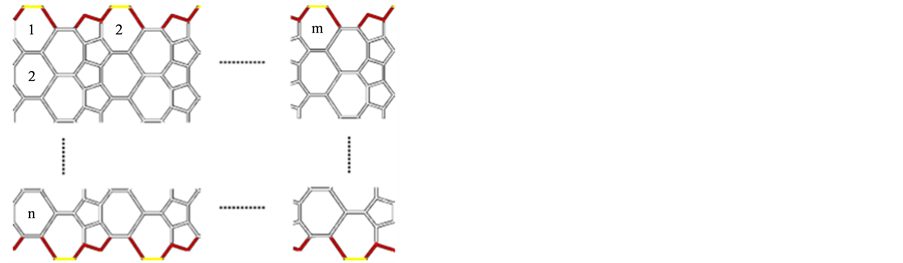
Figure 2. Pent-Heptagonal two-dimensional lattice of nanotubes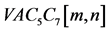
图2. Pent-Heptagonal纳米管的二维晶格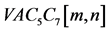
本文利用边集合划分方法得到Pent-Heptagonal纳米管若干基于度的拓扑指数计算公式。
2. 主要结果
将Pent-Heptagonal纳米管的顶点集和边集合作如下划分:
 ,
,
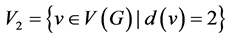 ,
,
 ,
,
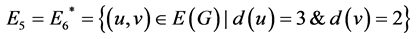 ,
,
 。
。
从图2来看,在Pent-Heptagonal纳米管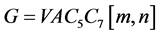 中分别用m和n来表示第一行和第一列的七边形数量,则有纳米管的顶点数
中分别用m和n来表示第一行和第一列的七边形数量,则有纳米管的顶点数 ,并且有:
,并且有:
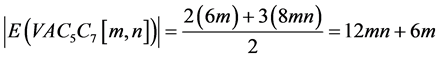
并且,我们在图2中用黄色标记 、
、 的边,用红色标记
的边,用红色标记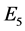 、
、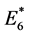 的边,
的边, 用白色标记。因此,得到
用白色标记。因此,得到 的大小等于
的大小等于 ,
,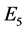 的大小为
的大小为 。换句话说,以上边的数量划分为
。换句话说,以上边的数量划分为 和
和 ,我们有以下的表格:
,我们有以下的表格:
于是,利用上表以及各种拓扑指数的定义,我们得到:
广义的Randić指数为:
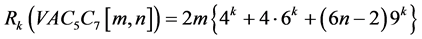
修改的第二Zagreb指数为:
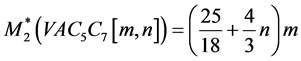
广义Zagreb指数为:
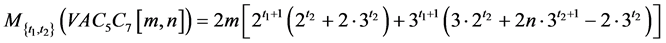
和连通指数为:
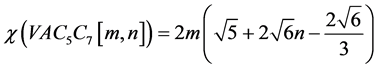
推广形式的和连通指数为:
调和指数为:
调和指数的广义形式为:
广义几何代数指数为:
 。
。
一般GA指数为:
 。
。
原子键连通指数为:
 。
。
两类Zagreb多项式分别为
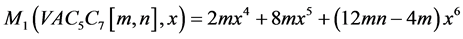 ,
,
 。
。
第三类Zagreb指数和多项式分别为:
 ,
,
 。
。
两类乘法Zagreb指数分别为:
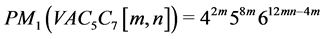
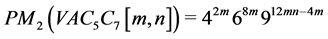 。
。
重新定义的三类Zagreb指数分别为:
 ,
,
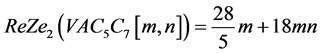 ,
,
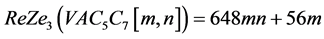 。
。
F指数为:
 。
。
M-多项式为
 。
。
广义ABC指数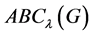 和and增强的Zagreb指数
和and增强的Zagreb指数 分别为:
分别为:
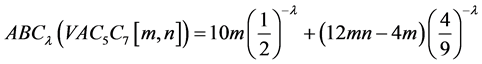 ,
,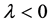
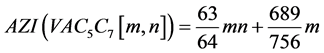 。
。
两类减弱的倒数Randić指数分别为
 。
。
第二减弱的倒数Randić指数定义为
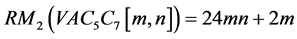 。
。
3. 总结
随着化学实验条件的改善和新化学生物技术的发现及应用,每年有大量复杂的化学分子被发现。在化学领域,化学家们会通过大量实验,来研究新物质的性质,比如:熔点、沸点、毒性、氧化性等等。因而对每年发现的大量新物质的研究需要大量仪器设备和药品试剂,造成了研究的高成本。但是,如果把化学分子的结构用图模型来表示的话,化学分子的特性就可以用一些参数来衡量,比如Zagreb指数、维纳指数、Randić指数等。本文利用边集合划分方法得到的Pent-Heptagonal纳米管若干基于度的拓扑指数计算公式,计算结果可运用到新化学分子的性质研究上,进而可以大大节约研究成本以及研究时间。
文章引用
何 静,高 炜. Pent-Heptagonal纳米管基于度的拓扑指数计算
Degree Based Topological Index Calculation of Pent-Heptagonal Nanotubes[J]. 理论数学, 2016, 06(03): 143-150. http://dx.doi.org/10.12677/PM.2016.63021
参考文献 (References)
- 1. Gutman, L., Ruscic, B., Trinajstic, N. and Wilcox, C.F. (1975) Graph Theory and Molecular Orbitals. Journal of Phys-ical Chemistry, 62, 3399-3406. http://dx.doi.org/10.1063/1.430994
- 2. Randić, M. (1975) On the Characterization of Molecular Branching. Journal of the American Chemical Society, 97, 6609-6615. http://dx.doi.org/10.1021/ja00856a001
- 3. Bondy, J.A. and Murty, U.S.R. (1976) Graph Theory with Applica-tions. Macmillan Press, London, 1-40. http://dx.doi.org/10.1007/978-1-349-03521-2
- 4. Balaban, A.T., Motoc, I., Bonchov, D. and Mekenyan, O. (1983) Topological Indices for Structure-Activity Correlations. Topics in Current Chemistry, 114, 21-55. http://dx.doi.org/10.1007/BFb0111212
- 5. Farahani, M.R. and Gao, W. (2015) On the Omega Polynomial of a Family of Hydrocarbon Moleculs “Polycyclic Aromatic Hydrocarbons PAHK”. Asian Academic Research Journal of Multidisciplinary, 2, 263-268.
- 6. Bollobas, B. and Erdos, P. (2015) Graph of Extremal Weights. Ars Combinatoria, 50, 225-233.
- 7. Gao, W. and Rajesh Kanna, M.R. (2015) The Connective Eccentric Index for an Infinite Family of Dendrimers. Indian Journal of Fundamental and Applied Life Sciences, 5, 766-771.
- 8. Mohammad, R.F. (2013) Connectivity Indices of Pent-Heptagonal Nanotubes. Advances in Materials and Corrosion, 2, 33-35.
- 9. Gao, W. and Wang, W.F. (2014) Second Atom-Bond Connectivity Index of Special Chemical Molecular Structures. Journal of Chemistry, Article ID: 906254.
- 10. Xi, W.F. and Gao, W. (2014) Geometric-Arithmetic Index and Zagreb Indices of Certain Special Molecular Graphs. Journal of Advances in Chemistry, 10, 2254-2261.
- 11. Farahani, M.R. and Gao, W. (2016) On Multiplicative and Redefined Version of Zagreb Indices of V-Phenylenic Nanotubes and Nanotorus. British Journal of Mathematics & Computer Science, 13, 1-8. http://dx.doi.org/10.9734/BJMCS/2016/22752
- 12. Farahani, M.R. (2013) Connectivity Indices of Pent-Heptagonal Nanotubes. Advance in Materials and Corrosion, 2, 33-35.
- 13. Azari, M. and Iranmanesh, A. (2011) Generalized Zagreb Index of Graphs. Studia Universitatis Babes-Bolyai, 56, 59- 70.
- 14. Eliasi, M. and Iranmanesh, A. (2011) On Ordinary Generalized Geometric-Arithmetic Index. Applied Mathematics Letters, 24, 582-587. http://dx.doi.org/10.1016/j.aml.2010.11.021
- 15. Estrada, E., Torres, L., Rodrıguez, L. and Gutman, I. (1988) Anatombond Connectivity Index: Modelling the Enthalpy of Formation of Alkanes. Indian Journal of Chemistry A, 37, 849-855.
- 16. Gutman, I. (2011) Multiplicative Zagreb Indices of Trees. Bulletin of the International Mathematical Virtual Institute, 1, 13-19.
- 17. Usha, A, Ranjini, P.S. and Lokesha, V. (2014) Zagreb Co-Indices, Augmented Zagreb Index, Redefined Zagreb Indices and Their Polynomials for Phenylene and Hexagonal Squeeze. Proceedings of Inter-national Congress in Honour of Dr. Ravi. P. Agarwal, Uludag University, Bursa.
- 18. Furtula, B. and Gutman, I. (2015) A Forgotten Topological Index. Journal of Mathematical Chemistry, 53, 1184-1190. http://dx.doi.org/10.1007/s10910-015-0480-z
- 19. Furtula, B., Graovac, A. and Vukicevi, D. (2010) Augmented Zagreb Index. Journal of Mathematical Chemistry, 48, 370-380. http://dx.doi.org/10.1007/s10910-010-9677-3