Pure Mathematics
Vol.06 No.05(2016), Article ID:18557,9
pages
10.12677/PM.2016.65055
Two New Eigenvalue Inclusion Sets for Tensors
Ruiyan Hu, Jing Zhao, Yaotang Li*
School of Mathematics and Statistics, Yunnan University, Kunming Yunnan

Received: Sep. 1st, 2016; accepted: Sep. 16th, 2016; published: Sep. 20th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The concept of tensors is a generalization of matrices to high order. And there are some important applications in many scientific fields, such as data analysis, signal and image processing and so on. Tensor eigenvalue theory is an important aspect of tensor research and application. In this paper, two new eigenvalue inclusion sets for tensors are given, and it is proved that the new eigenvalue inclusion sets are tighter than the classical Gersgorin inclusion set. In addition, as applications of the results, two sufficient conditions for the (semi-)positive definite property of the even order symmetric tensors are obtained.
Keywords:Tensor, Eigenvalue Inclusion Set, Symmetric Tensor, Positive Definite

两个新的张量特征值包含区域
胡汭炎,赵晶,李耀堂*
云南大学数学与统计学院,云南 昆明

收稿日期:2016年9月1日;录用日期:2016年9月16日;发布日期:2016年9月20日

摘 要
张量是矩阵的高阶推广,在数据分析、信号与图像处理等许多科学领域中都有重要应用,而张量的特征值是张量理论和应用研究的一个重要方面。本文给出了两个新的张量特征值包含集,证明了所得的包含集含于经典的Gersgorin特征值包含集中,并由其得到偶数阶实对称张量(半)正定性的两个充分条件。
关键词 :张量,特征值包含集,对称张量,正定性

1. 引言
张量是矩阵的高阶推广,在信号图像处理 [1] ,非线性优化 [2] ,高阶统计学 [3] ,数据挖掘与处理 [1] 和弹性分析 [4] 等方面有重要的应用。
设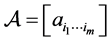 ,若
,若 ,其中
,其中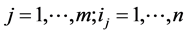 ,则称
,则称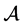 为m阶n维的复(实)张量,记作
为m阶n维的复(实)张量,记作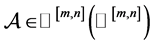 。显然,向量是一阶张量,矩阵是二阶张量。此外,若存在复(实)
。显然,向量是一阶张量,矩阵是二阶张量。此外,若存在复(实)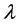 和非零向量
和非零向量 满足多元齐次方程:
满足多元齐次方程:
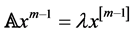 ,
,
则称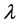 为
为 的特征值,
的特征值,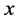 为
为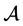 的相应于
的相应于 的特征向量,其中
的特征向量,其中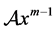 和
和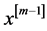 为n维向量,其第
为n维向量,其第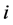 个元素分别为:
个元素分别为:
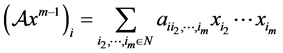 和
和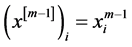 。
。
若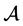 和
和 是实的,则
是实的,则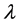 是实的,这时称
是实的,这时称 为张量
为张量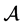 的H-特征值。
的H-特征值。
设张量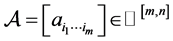 ,若它的每一个元素
,若它的每一个元素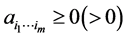 ,则称
,则称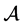 为非负(正)张量,记作
为非负(正)张量,记作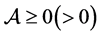 。若对任意
。若对任意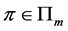 都有:
都有:
 ,
,
则称 为对称张量 [5] ,其中
为对称张量 [5] ,其中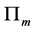 是指标为
是指标为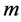 的置换群。令
的置换群。令 为Kronecher符号,即若
为Kronecher符号,即若 ,则
,则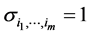 ,否则
,否则 。用
。用 表示m阶n维单位张量,其元素如下:
表示m阶n维单位张量,其元素如下:
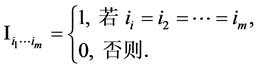
设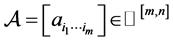 ,若
,若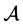 的所有特征值都不为零,则称
的所有特征值都不为零,则称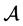 是非奇异的。称
是非奇异的。称 为Z-张量,如果它的所有非对角元非正,即
为Z-张量,如果它的所有非对角元非正,即 可表示为
可表示为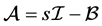 ,其中
,其中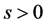 ,
, ( [6] ,定义3)。此外,若
( [6] ,定义3)。此外,若 ,则称
,则称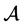 为M-张量;若
为M-张量;若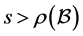 ,则称
,则称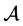 为非奇异的M-张量( [6] ,定义4)。
为非奇异的M-张量( [6] ,定义4)。
定义1.1 ( [6] ,定义8) 设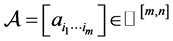 ,用
,用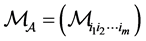 表示
表示 的比较张量,其中:
的比较张量,其中:

定义1.2 ( [6] ,定义9) 若张量 的比较张量
的比较张量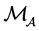 是M-张量,则称
是M-张量,则称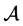 为H-张量。若张量
为H-张量。若张量 的比较张量
的比较张量 是非奇异的M-张量,则称
是非奇异的M-张量,则称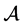 为强H-张量。
为强H-张量。
设 ,定义
,定义 次齐次
次齐次 元多项式
元多项式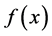 如下:
如下:
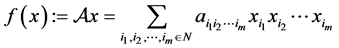 ,
, 。
。
设张量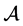 为偶数阶的实对称张量,若对任意的非零向量
为偶数阶的实对称张量,若对任意的非零向量 ,
,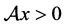 (
( ),则
),则 是正(半)定的。
是正(半)定的。
定理1.1 ( [5] ,定理5)设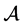 是偶数阶实对称张量,则
是偶数阶实对称张量,则 是正(半)定的当且仅当
是正(半)定的当且仅当 的所有H-特征值是正(非负)的。
的所有H-特征值是正(非负)的。
张量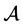 的所有特征值构成的集合称为
的所有特征值构成的集合称为 的谱,记作
的谱,记作 。张量的特征值在张量理论和应用中具有特别重要的意义,然而当张量的阶数和维数较高时,张量特征值的精确计算却是相当困难的。因此,张量特征值的定位和估计成为当今学者们研究的一个热门问题 [5] [7] - [9] 。祁在 [5] 中把关于矩阵的著名的Gerschgorin特征值包含定理推广到实对称张量,这个结果很容易推广到一般的张量中,即有:
。张量的特征值在张量理论和应用中具有特别重要的意义,然而当张量的阶数和维数较高时,张量特征值的精确计算却是相当困难的。因此,张量特征值的定位和估计成为当今学者们研究的一个热门问题 [5] [7] - [9] 。祁在 [5] 中把关于矩阵的著名的Gerschgorin特征值包含定理推广到实对称张量,这个结果很容易推广到一般的张量中,即有:
定理1.2 ( [5] ,定理6) 设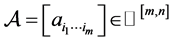 ,则
,则
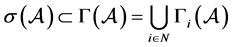 ,
,
其中 ,
,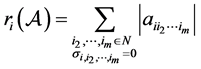 。
。
2015年,Li等在文 [9] 中又给出张量特征值的如下包含区域。
定理1.3 ( [9] ,定理2.1) 设 ,
,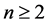 ,则
,则
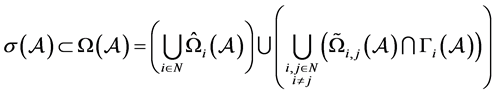
其中:
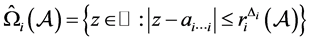 ;
;
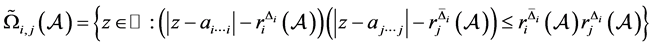 ;
;
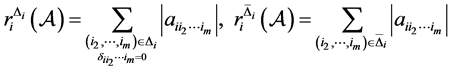 ;
;
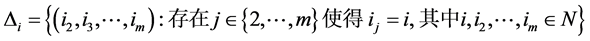 ;
;
 。
。
定理1.4 ( [9] ,定理2.3) 设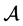 是m阶n维复张量,
是m阶n维复张量,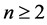 ,则:
,则: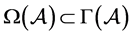 。
。
本文继续张量特征值的定位问题的研究。在第二节,给出两个新的张量特征值包含区域,并对得到的包含区域进行比较。在第三节给出几个数值例子。在第四节,应用所获张量特征值包含区域给出张量正定(半正定)的几个充分性条件。
2. 新的张量特征值包含区域
最近,Wang等在文 [10] 给出了张量的一个如下非奇异性条件。
引理2.1 ( [10] ,定理3.1) 设 ,若
,若
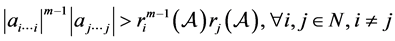 ,
,
则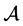 是非奇异的H-张量。
是非奇异的H-张量。
可得下面的张量的特征值包含区域。
定理2.1 设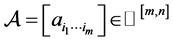 ,
,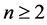 ,则
,则
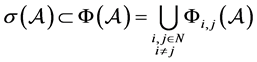 ,
,
其中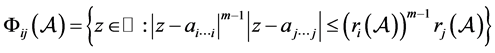 。
。
证明:设 ,则
,则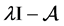 是奇异的。若
是奇异的。若 ,则
,则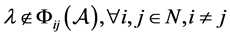 ,即
,即
 。
。
再由引理2.1知 是非奇异的,产生矛盾,故
是非奇异的,产生矛盾,故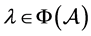 。
。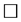
注2.1:当 ,即
,即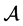 退化为矩阵时:
退化为矩阵时:
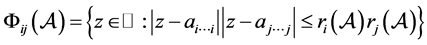 。
。
这时定理2.1就是矩阵的Brauer特征值包含定理。
下面我们给出另一个张量特征值包含区域。
定理2.2 设 ,
,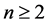 ,则:
,则:
 ,
,
其中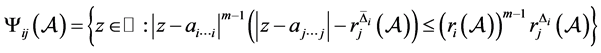 。
。
证明:对于任意的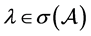 ,设
,设 是相应的特征向量,则
是相应的特征向量,则
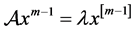 。 (1)
。 (1)
设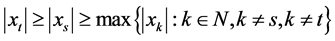 ,则
,则 。由(1)式得:
。由(1)式得:
 ,
,
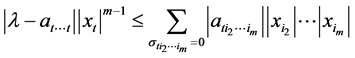 。
。
因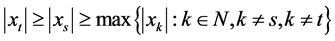 ,故
,故
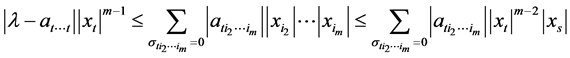 。
。
又因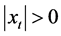 ,对上述不等式两边同时除以
,对上述不等式两边同时除以 得:
得:
 。
。
于是有
 (2)
(2)
同样由(1)式可得
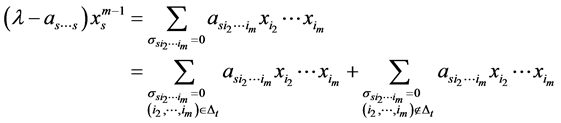 。
。
对上述不等式两边取绝对值得
 ,
,
移项得
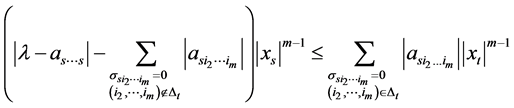 。(3)
。(3)
现分两种情况讨论,若 ,由(2)式得
,由(2)式得 ,显然
,显然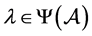 ;若
;若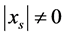 ,由不等式(2)乘不等式(3)得:
,由不等式(2)乘不等式(3)得:
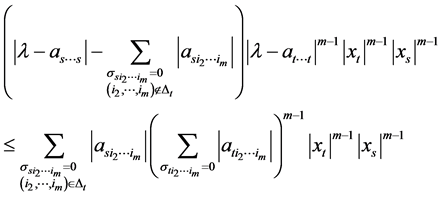 。
。
因为 ,对上述不等式两边同时除以
,对上述不等式两边同时除以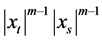 得
得
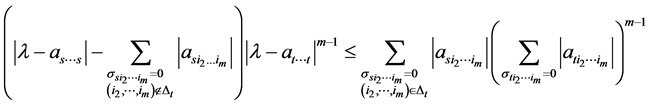 。
。
上述式子表明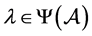 。因此
。因此 。
。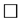
注2.2 当 ,即
,即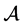 退化为矩阵时,
退化为矩阵时,
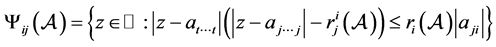 。
。
这时定理2.2就是矩阵的D-Z矩阵特征值包含定理。
下面我们对上述特征值包含区域进行比较。
定理2.3 设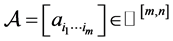 ,
,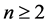 ,则
,则
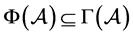 ,
, 。
。
证明:首先证明 。设
。设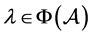 。则存在
。则存在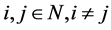 使得
使得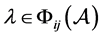 ,即:
,即:
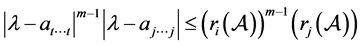 。 (4)
。 (4)
当 时,由(4)式可得
时,由(4)式可得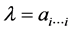 或
或 。则
。则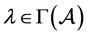 。当
。当 时,由(4)式可得:
时,由(4)式可得:
 。
。
即:
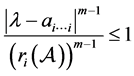 或
或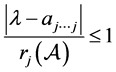 。
。
由上式得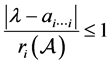 或
或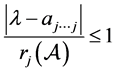 。于是
。于是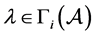 或
或 ,因而
,因而 ,故
,故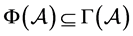 。
。
下证: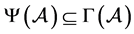 。设
。设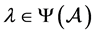 ,则存在
,则存在 使得
使得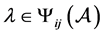 ,即
,即
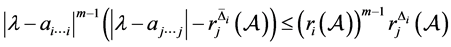 。 (5)
。 (5)
当 时,由(5)式得
时,由(5)式得 或
或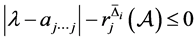 ,于是有
,于是有
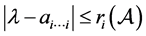 或
或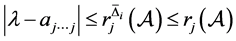 ,即或
,即或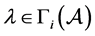 或
或 ,因而
,因而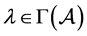 。当
。当 时,由(5)式得
时,由(5)式得
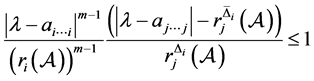 。
。
于是
 或
或 。
。
即
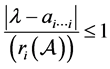 或
或 。
。
上式表明 或
或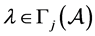 ,因而
,因而 。由此知
。由此知 。
。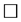
由于理论上无法比较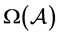 、
、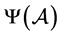 和
和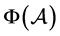 三者的大小,下节我们用三个数值例子对其比较。
三者的大小,下节我们用三个数值例子对其比较。
3. 数值例子
本节我们用三个数值例子对本文的结果进行解释。
例3.1. 考虑二阶张量
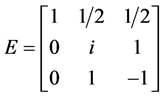
分别应用定理2.1和定理2.2得到:
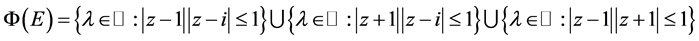 ,
,
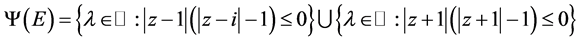 。
。
图1表明对于此张量有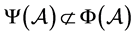 和
和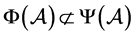 。
。
例3.2. 设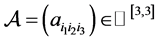 ,其中
,其中 ,其他的元素都为零。分别应用定理1.2、定理2.1和定理2.2得到:
,其他的元素都为零。分别应用定理1.2、定理2.1和定理2.2得到:
 。
。
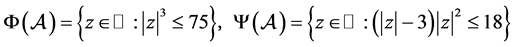 。
。
图2表明对于此张量有 。
。
例3.3. 设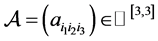 ,其中
,其中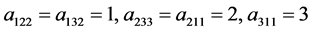 ,其他的元素都为零。分别应用定理1.2、定理1.3和定理2.1得到:
,其他的元素都为零。分别应用定理1.2、定理1.3和定理2.1得到:
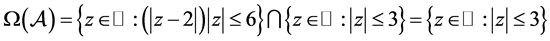 ,
,
 ,
,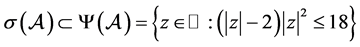 。
。
图3表明对于此张量有 。
。
上面三个例子表明在某些情况下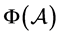 和
和 比
比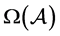 小,在某些情况下
小,在某些情况下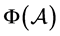 和
和 比
比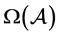 大。
大。
4. 偶数阶实对称张量正定性的判定
应用第二节得结果,本节给出偶数阶实对称张量正(半正)定性的两个充分条件。
定理4.1 设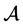 是偶数阶实对称张量,且
是偶数阶实对称张量,且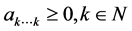 ,若对于任意的
,若对于任意的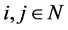 ,
, 都有:
都有:
 (6)
(6)
则 是正定的。
是正定的。
证:设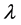 是
是 的H-特征值。由定理2.1知,
的H-特征值。由定理2.1知,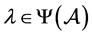 ,则存在
,则存在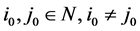 使得
使得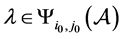 ,即:
,即:
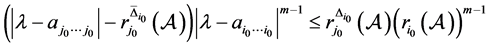 。 (7)
。 (7)
假若 ,则因
,则因 和(7)式成立,故:
和(7)式成立,故:
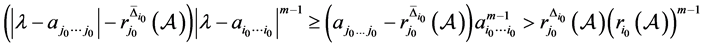
这与(8)式矛盾,因此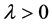 。再由定理1.1知
。再由定理1.1知 是正定的。
是正定的。
类似地可证如下结论。
定理4.2 设 是偶数阶实对称张量,且
是偶数阶实对称张量,且 ,若对于任意的
,若对于任意的 ,
,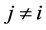 都有:
都有:
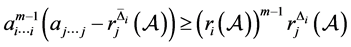
则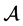 是正半定的。
是正半定的。
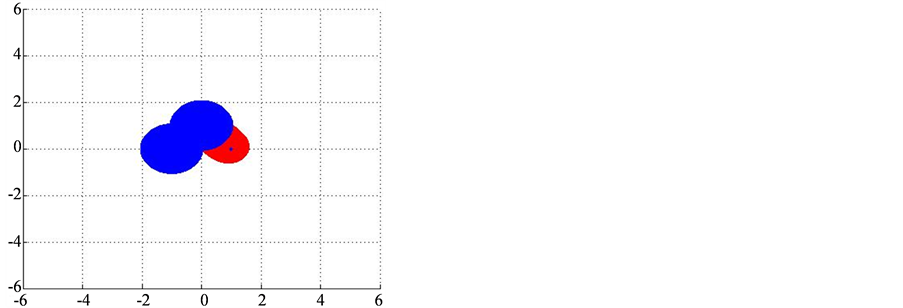
Figure 1. The comparison of 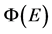 ,
, 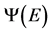
图1.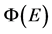 和
和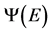 关系图
关系图
注:蓝色为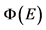 ,红色为
,红色为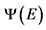 。
。
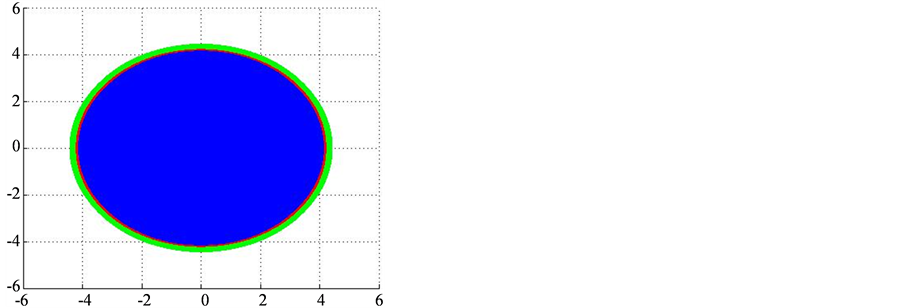
Figure 2.The comparison of 
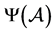
图2. 和
和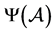 关系图
关系图
注:图中蓝色为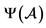 ,红色区域为
,红色区域为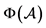 ,绿色为
,绿色为 。
。
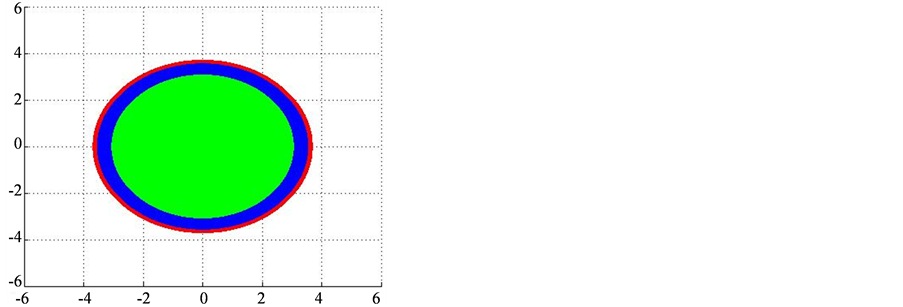
Figure 3.The comparison of 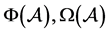

图3.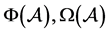 和
和 关系图
关系图
注:图中蓝色为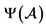 ,红色区域为
,红色区域为 ,绿色为
,绿色为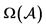
例3. 设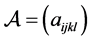 是4阶2维的实对称张量,其中
是4阶2维的实对称张量,其中
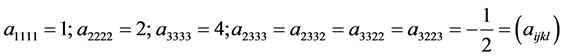

其它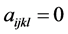 。通过计算知张量
。通过计算知张量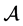 满足定理4.1的条件,则
满足定理4.1的条件,则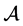 是正定的。事实上,通过 [2] 中推论2可得到
是正定的。事实上,通过 [2] 中推论2可得到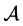 的H-特征值为
的H-特征值为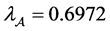 。由定义4.1知
。由定义4.1知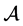 确实是正定的。
确实是正定的。
基金项目
本文受国家自然科学基金资助项目(11361074)资助。
文章引用
胡汭炎,赵 晶,李耀堂. 两个新的张量特征值包含区域
Two New Eigenvalue Inclusion Sets for Tensors[J]. 理论数学, 2016, 06(05): 402-410. http://dx.doi.org/10.12677/PM.2016.65055
参考文献 (References)
- 1. Nikias, C.L. and Mendel, J.M. (1993) Signal Processing with Higher-Order Spectra. IEEE Signal Processing Magazine, 10, 10-37.
- 2. Qi, L., Wang, F. and Wang, Y. (2009) Z-Eigenvalue Methods for a Global Polynomial Optimization Problem. Mathematical Programming, 118, 301-316. http://dx.doi.org/10.1007/s10107-007-0193-6
- 3. Ching, W. and Ng, M. (2006) Markov Chains: Models, Algorithms and Applications. Int. Ser. Oper. Res .Manag. Sci. Springer, New York.
- 4. Bose, N.K. and Kamat, P.S. (1975) Algorithm for Stability Test of Multidimensional Filters. IEEE Transactions on Acoustics, Speech, and Signal Processing, 20, 169-175.
- 5. Qi, L. (2005) Eigenvalues of a Real Supersymmetric Tensor. Journal of Symbolic Computation, 40, 1302-1324.
- 6. Ding, W.Y., Qi, L.Q. and Wei, Y.M. (2013) M-Tensors and Nonsingular M-Tensors. Linear Algebra and Its Applications, 439, 3264-3278.
- 7. Cartwright, D. and Sturmfels, B. (2010) The Number of Eigenvalues of Tensors. ar-Xiv:1004.4953vl, Apr.
- 8. Kolda, T.G. and Mayo, J.R. (2011) Shifted Power Method for Computing Tensor Eigenpairs. ar-Xiv:1007.1267v2, Math. NA.
- 9. Li, C.Q., Zhou, J.J. and Li, Y.T. (2015) A New Brauer-Type Eigenvalue Localization Set for Tensors. Linear and Multilinear Algebra, 64, 727-736. http://dx.doi.org/10.1080/03081087.2015.1119779
- 10. Wang, Y.J., Zhou, G.L. and Caccetta, L. (2016) Nonsingular H-Tensors and Their Criteria. Journal of Industrial & Management Optimization, 12, 1173-1186. http://dx.doi.org/10.3934/jimo.2016.12.1173
*通讯作者。