Pure Mathematics
Vol.07 No.04(2017), Article ID:21210,6
pages
10.12677/PM.2017.74029
Node-Disjoint Shortest and Next-to-Shortest Paths in N-Dimensional Hypercube
Yunxia Zhang
Shanxi Finance and Taxation College, Taiyuan Shanxi

Received: Jun. 12th, 2017; accepted: Jun. 26th, 2017; published: Jun. 30th, 2017

ABSTRACT
N-dimensional hypercube is widely used in the field of parallel computer systems. The special topological structure of n-dimensional hypercube has significantly affected the performance of large multiprocessor systems. In this article, we prove the following result: In n-dimensional hypercube, for any two nodes with hamming distance that equals to k, there are k node-disjoint shortest paths of length k. Additionally, if we include nest-to-shortest paths of length k + 2 in addition to shortest paths, there will be n node-disjoint paths in total.
Keywords:Hypercube, Node-Disjoint Path, Shortest Paths, Next-to-Shortest Paths
超立方体中最短和次短的点不交路径
张云霞
山西省财政税务专科学校,山西 太原
收稿日期:2017年6月12日;录用日期:2017年6月26日;发布日期:2017年6月30日

摘 要
n维超立方体在并行计算领域有着广泛的应用,其特殊的拓扑结构对大规模的多处理器系统的性能具有重要的影响。本文研究n维超立方体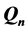 的最短路径问题,采用构造的方法证明了以下结论:
的最短路径问题,采用构造的方法证明了以下结论: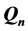 中任意两点之间一定存在k条不交的长度为k的最短路径,其中k为此两点之间的Hamming距离。此外,如果放宽最短路径的条件,对两点之间的 距离为k的点,长度最多为
中任意两点之间一定存在k条不交的长度为k的最短路径,其中k为此两点之间的Hamming距离。此外,如果放宽最短路径的条件,对两点之间的 距离为k的点,长度最多为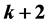 的不交路径存在至少n条。
的不交路径存在至少n条。
关键词 :超立方体,点不交路径,最短路径,次短路径

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着超大规模集成电路工艺的发展,集成巨量处理器(可达216)的大规模处理器成为了未来的主要发展趋势。为了提高并行计算系统的效率,科学界一直在寻找结构简单、延展性好、节点度小的互联网络拓扑结构。而超立方体由于其特殊的拓扑结构,例如它的对称性、强容错性、正则性等性质,使得它成为了最为重要和应用最广泛的并行计算机互联网络拓扑结构。
在实际应用和理论研究方面,超立方体在近年都得到了高度关注。基于超立方体的各种可扩展并行计算互联网络系统应运而生。文献 [1] 涉及了超立方体在业界的实际应用和专利申请。
近年来,更多的文献专注于挖掘超立方体的性质和结构,如文献 [2] ,从应用的角度综合探讨了超立方体中一对一、一对多的不相交路径存在问题。文献 [3] 后续讨论了一对多节点的不相交路径的相应算法,并给出了时间复杂度为 的计算该路径的算法,其中n为该超立方体的维度,m为从同一点出发抵达的目标节点的数量。文献 [4] 、文献 [5] 讨论了多对多点不交路径存在问题,并进一步的多对多点不交路径的高效算法。讨论了连通度的概念以及其与多对多点不交路径上限之间的联系。
的计算该路径的算法,其中n为该超立方体的维度,m为从同一点出发抵达的目标节点的数量。文献 [4] 、文献 [5] 讨论了多对多点不交路径存在问题,并进一步的多对多点不交路径的高效算法。讨论了连通度的概念以及其与多对多点不交路径上限之间的联系。
本文主要研究n维超立方体 的最短路径问题,采用构造的方法证明了以下结论:
的最短路径问题,采用构造的方法证明了以下结论: 中任意两点之间一定存在k条不交的长度为k的最短路径,其中k为此两点之间的 距离。此外,如果放宽最短路径的条件,对两点之间的 距离为k的点,长度最多为
中任意两点之间一定存在k条不交的长度为k的最短路径,其中k为此两点之间的 距离。此外,如果放宽最短路径的条件,对两点之间的 距离为k的点,长度最多为 的不交路径存在至少n条。在文献 [6] 中,通过数学归纳法证明了
的不交路径存在至少n条。在文献 [6] 中,通过数学归纳法证明了 中任意两点(Hamming距离为k)之间一定存在k条不交的长度为k的最短路径。本文简化了上述证明,并在此基础上,通过放宽最短路径的条件至次短路径,扩充了该结论,从而构造出了至少n条点不交的最短路径。该结论在并行计算机互联网络拓扑结构中有大量可能的应用,并可以作为实际应用的理论基础。文献 [7] 中,针对并行计算系统的另一应用广泛的结构递归循环网络,给出了一点对多点的最短和次短的点不交路构造,与本文研究的问题有一定的相似性,也具有广泛的应用价值。
中任意两点(Hamming距离为k)之间一定存在k条不交的长度为k的最短路径。本文简化了上述证明,并在此基础上,通过放宽最短路径的条件至次短路径,扩充了该结论,从而构造出了至少n条点不交的最短路径。该结论在并行计算机互联网络拓扑结构中有大量可能的应用,并可以作为实际应用的理论基础。文献 [7] 中,针对并行计算系统的另一应用广泛的结构递归循环网络,给出了一点对多点的最短和次短的点不交路构造,与本文研究的问题有一定的相似性,也具有广泛的应用价值。
不仅对于次长路径,超立方体上最长路径的可能最大值也得到了学界的关注和研究。在文献 [8] 中,对于两节点之间路径的最长距离进行了分情况的讨论,并在两种条件下减小了最长距离的最大值。
在文献 [9] 中,针对分层超立方体互联网络,其中两节点之间的点不交路得到了研究。不仅给出了点不交路最大数量的构造,同时也给出了这些路的长度最大值。
从另一方面,在超立方体上给定k对互不相同的节点,如何寻找它们之间的k条点不交路并覆盖超立方体中每一个节点,在文献 [10] 中得到了充分的研究。
2. 预备知识
本文中所有出现的无向图均为简单无向图,即无自环、无平行边的无向图。
以下为超立方体互联网络的定义。
定义1.1对于简单无向图,分别表示的顶点集和边集。称作n维超立方体互联网络当且仅当:
1) 的节点数量为,边的数量为。
2) 对任意的顶点,可以用维的二进制序列来表示。即。
3) 对于任意两顶点,其间有边当且仅当它们的二进制编码串只相差一位。
图1为1维和2维超立方体互联网络。
对于超立方体互联网络 ,若
,若 ,且任意两点之间互不相同,
,且任意两点之间互不相同, ,那么称
,那么称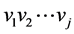 为
为 中的一条路。记为
中的一条路。记为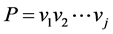 。如果
。如果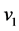 和
和 之间有k条不同路径,且对其中任意的两条路径,除了起点和终点之外,其中任意两节点不相同,那么称
之间有k条不同路径,且对其中任意的两条路径,除了起点和终点之外,其中任意两节点不相同,那么称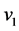 和
和 之间有k条点不交的路径。图2给出了超立方体互联网络
之间有k条点不交的路径。图2给出了超立方体互联网络 中点
中点 之间的两条点不交路径(虚线)。
之间的两条点不交路径(虚线)。
以下为Hamming距离的定义。需要注意的是,在信息论中,两个等长字符串之间的Hamming距离是两个字符串对应位置的不同字符的个数。而对于超立方体互联网络来说,需要计算的字符串都是二进

Figure 1. Hypercube 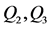
图1. 超立方体互联网络

Figure 2. Node disjoint path in Hypercube
图2. 超立方体互联网络中的点不交路径
制的。而对于二进制字符串来说,Hamming距离就是1的个数,因此有了以下定义。
定义1.2对于超立方体互联网络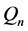 ,
,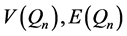 分别表示
分别表示 的点集和边集。
的点集和边集。 ,
, ,
, ,那么
,那么 之间的Hamming距离定义为
之间的Hamming距离定义为 。
。
我们知道,超立方体互联网络 的连通度是n。
的连通度是n。 的连通度条件构成了其满足性质
的连通度条件构成了其满足性质 的必要条件。这里性质
的必要条件。这里性质 指:在图
指:在图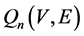 中,如果给定k对互不相同的节点,那么这k对点之间一定存在k条路径,且这k条路径之间是点不交的。文献 [5] 中不仅阐述了超立方体互联网络
中,如果给定k对互不相同的节点,那么这k对点之间一定存在k条路径,且这k条路径之间是点不交的。文献 [5] 中不仅阐述了超立方体互联网络 的连通度与性质
的连通度与性质 的关系,并给出了对任意的k对点
的关系,并给出了对任意的k对点 之间给出点不交的k条路径的算法。此算法的时间复杂度为
之间给出点不交的k条路径的算法。此算法的时间复杂度为 ,给出路径的最大长度为
,给出路径的最大长度为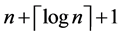 。
。
3. 主要结论
首先根据超立方体互联网络的性质,我们可以得到如下定理:
定理2.1设 且
且 ,则在
,则在 中
中 之间至多存在k条长度为k的点不交路径;且
之间至多存在k条长度为k的点不交路径;且 之间至多存在n条点不交路径。
之间至多存在n条点不交路径。
证明:
考虑到长度为k的路径一定为 之间的最短路径,因此路径一定是持续沿着减少两点之间Hamming距离的方向进行。而
之间的最短路径,因此路径一定是持续沿着减少两点之间Hamming距离的方向进行。而 的邻接节点中符合条件的恰为k个,因此符合条件的点不交路径一定不会超过k条。
的邻接节点中符合条件的恰为k个,因此符合条件的点不交路径一定不会超过k条。
另一方面, 中每个点的度均为n,因此两点之间至多存在n条点不交路径。□
中每个点的度均为n,因此两点之间至多存在n条点不交路径。□
接下来,我们给出文献 [6] 中结论的一种构造证明:
定理2.2设 且
且 ,则在
,则在 中
中 之间存在k条长度为k的点不交路径。
之间存在k条长度为k的点不交路径。
证明:
记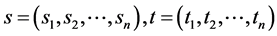 ,此处我们只需要考虑
,此处我们只需要考虑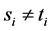 的位置。因为
的位置。因为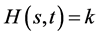 ,我们不妨假设
,我们不妨假设 。进一步我们可以假设
。进一步我们可以假设 而不影响命题的一般性。
而不影响命题的一般性。
因此原命题等价于在 中
中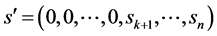 与
与 之间存在k条长度为k的点不交路径。由于
之间存在k条长度为k的点不交路径。由于 ,我们在下面的叙述中省略坐标的后
,我们在下面的叙述中省略坐标的后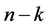 位。
位。
考虑以下k条路径 :
:
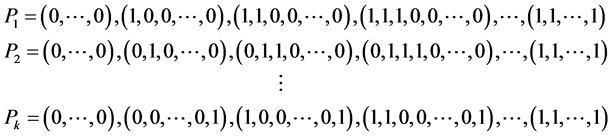
即 从
从 起始,以从第i位开始依次由0变成1的方式行进,直至到达
起始,以从第i位开始依次由0变成1的方式行进,直至到达 。显然
。显然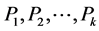 均为长度为k的路径,只需证明他们除了
均为长度为k的路径,只需证明他们除了 之外不经过相同的顶点。若
之外不经过相同的顶点。若 经过相同的顶点v,假设v的坐标中有t个1,根据构造容易知道在
经过相同的顶点v,假设v的坐标中有t个1,根据构造容易知道在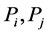 中经过的坐标中t个1的顶点显然不同。
中经过的坐标中t个1的顶点显然不同。
因此, 即为满足条件的k条长度为k的点不交路径。□
即为满足条件的k条长度为k的点不交路径。□
可以看出,定理2.2中的构造也达到了定理2.1中证明的 之间长度为k的点不交路径的上限。此外,对于
之间长度为k的点不交路径的上限。此外,对于 的两个节点
的两个节点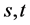 ,他们之间的次长路径长度为
,他们之间的次长路径长度为 (由于超立方体的结构特性汉明距离为k的两点之间不存在长度为
(由于超立方体的结构特性汉明距离为k的两点之间不存在长度为 的路径)。如果我们考虑超立方体中两点之间的次长路径,可以得到如下结论:
的路径)。如果我们考虑超立方体中两点之间的次长路径,可以得到如下结论:
定理2.3设 且
且 ,则在
,则在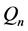 中
中 之间至少存在
之间至少存在 条长度为
条长度为 的点不交路径。
的点不交路径。
证明:
记 ,此处我们只需要考虑
,此处我们只需要考虑 的位置。因为
的位置。因为 ,我们不妨假设
,我们不妨假设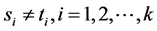 。进一步我们可以假设
。进一步我们可以假设 ,
, ,
, 而不影响命题的一般性(以下在坐标中用“|”来分隔第
而不影响命题的一般性(以下在坐标中用“|”来分隔第 位)。
位)。
因此原命题等价于证明在 中
中 与
与 之间存在
之间存在 条长度为
条长度为 的点不交路径。
的点不交路径。
考虑以下 条路径
条路径 :
:

即 从
从 起始,先将第
起始,先将第 位由0变成1,之后依次将前k位由0变成1,最后将第
位由0变成1,之后依次将前k位由0变成1,最后将第 位由1还原成0到达
位由1还原成0到达 。显然
。显然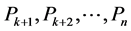 均为长度为
均为长度为 的路径,且因为不同路径之间除了
的路径,且因为不同路径之间除了 之外其他中间节点后
之外其他中间节点后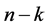 位不相同,因此他们除了
位不相同,因此他们除了 之外不经过相同的顶点。
之外不经过相同的顶点。
因此, 即为满足条件的
即为满足条件的 条长度为
条长度为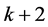 的点不交路径。□
的点不交路径。□
根据定理2.2和定理2.3的构造,我们容易得出如下推论:
推论2.1设 且
且 ,则在
,则在 中
中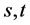 之间存在n条长度不超过
之间存在n条长度不超过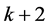 的点不交路径。
的点不交路径。
证明:
类似于定理2.3,原命题等价于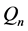 中
中 与
与 之间存在
之间存在 条长度为
条长度为 的点不交路径(在坐标中用“|”来分隔第
的点不交路径(在坐标中用“|”来分隔第 位)。
位)。
考虑定理2.2和定理2.3的证明中构造的n条路径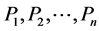 。显然
。显然 均为长度不超过
均为长度不超过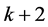 的路径,又因为
的路径,又因为 经过的中间节点后
经过的中间节点后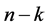 位不相同,因此他们除了
位不相同,因此他们除了 之外不经过相同的顶点。
之外不经过相同的顶点。
因此, 即为满足条件的n条长度不超过
即为满足条件的n条长度不超过 的点不交路径。□
的点不交路径。□
4. 结语
本文研究了超立方体互联网络中两点之间点不交路径的性质。对于原有的关于两点之间点不交最短路径的结论,给出了更加简洁直接的构造证明。并且在此基础上,对于两点之间点不交的次短路径进行了讨论,并且进行了构造。最终证明超立方体互联网络中两点之间的点不交最短和次短路径数量最多可以达到超立方体可容纳的点不交路径的上限。该结论在并行计算机互联网络拓扑结构中有大量可能的应用,并可以作为实际应用的理论基础。
项目信息
山西省科学技术厅软科学项目(NO2016041038-5)。
文章引用
张云霞. 超立方体中最短和次短的点不交路径
Node-Disjoint Shortest and Next-to-Shortest Paths in N-Dimensional Hypercube[J]. 理论数学, 2017, 07(04): 230-235. http://dx.doi.org/10.12677/PM.2017.74029
参考文献 (References)
- 1. 刘有耀, 杨晓强, 杜慧敏, 等. 一种基于超立方体的可扩展并行计算互连网络拓扑结构[P]. 中国专利, 专利号CN101414952A, 2009-4-22. https://docs.google.com/viewer?url=patentimages.storage.googleapis.com/pdfs/ 5564d7271574b36e509f/CN101414952A.pdf. http://xueshu.baidu.com/s?wd=paperuri%3A%281dc376a4b0d242325b1c8fc 763410a55%29&filter=sc_long_sign&tn=SE_xueshus ource_2kduw22v&sc_vurl=http%3A%2F%2Fd.wanfangd ata.com.cn%2FPatent_CN200810232462.0.aspx&ie=utf-8&sc_us=18417171916466020850
- 2. Lai, C.N. (2012) Optimal Construction of All Shortest Node-Disjoint Paths in Hypercubes with Applications. IEEE Transactions on Parallel and Distributed System, 23, 1129-1134. https://doi.org/10.1109/TPDS.2011.261
- 3. Lai, C.N. (2015) Constructing All Shortest Node-Disjoint Paths in Torus Networks. Journal of Parallel and Distributed Computing, 75, 123-132. https://doi.org/10.1016/j.jpdc.2014.09.004
- 4. Chen, X.B. (2013) Paired Many-to-Many Disjoint Path Covers of Hypercubes. Information Sciences, 236, 218-223. https://doi.org/10.1016/j.ipl.2011.10.010
- 5. Gu, Q.-P. and Peng, S. (2000) An Efficient Algorithm for the K-Pairwise Disjoint Paths Problem in Hypercubes. Journal of Parallel and Distributed Computing, 60, 764-774. http://www.sciencedirect.com/science/article/pii/S0743731500916320 https://doi.org/10.1006/jpdc.2000.1632
- 6. 陈荷花, 高太平. n维超立方体中点不交的最短路径[J]. 山西大学学报(自然科学版), 2016, 39(2): 229-232. https://doi.org/10.13451/j.cnki.shanxi.univ(nat.sci.).2016.02.011
- 7. Chung, I. (2013) Design of a Set of One-to-Many Node-Disjoint and Nearly Shortest Paths on Recursive Circulant Networks. Journal of Korea Multimedia Society, 16, 897-904. https://doi.org/10.9717/kmms.2013.16.7.897
- 8. Lai, C.N. (2012) Two Conditions for Reducing the Maximal Length of Node-Disjoint Paths in Hypercubes. Theoretical Computer Science, 418, 82-91. https://doi.org/10.1016/j.tcs.2011.11.009
- 9. Wu, R.Y., Chen, G.H., Kuo, Y.L., et al. (2012) Node-Disjoint Paths in Hierarchical Hypercube Networks. Information Sciences, 177, 4200-4207. https://doi.org/10.1016/j.ins.2007.02.035
- 10. Joa, S., Parkb, J.-H. and Chwaa, K.Y. (2013) Paired 2-Disjoint Path Covers and Strongly Hamiltonian Laceability of Bipartite Hypercube-Like Graphs. Information Sciences, 242, 103-112. https://doi.org/10.1016/j.ins.2013.04.013