Pure Mathematics
Vol.08 No.03(2018), Article ID:24812,7
pages
10.12677/PM.2018.83026
Oscillate Criterion for Second-Order Nonlinear Differential Equations
Xinxiao Su*, Lina Dai, Quanwen Lin
Department of Mathematics, School of Science, Guangdong University of Petrochemical Technology, Maoming Guangdong

Received: Apr. 19th, 2018; accepted: May 3rd, 2018; published: May 10th, 2018

ABSTRACT
Using Riccati-transform, we further study second-order nonlinear differential equations of the form We get some new oscillate criteria.
Keywords:Generalized Riccati-Transform, Nonlinear, Differential Equations, Oscillate Criterion

二阶非线性微分方程的振动准则
苏新晓*,戴丽娜,林全文
广东石油化工学院理学院数学系,广东 茂名

收稿日期:2018年4月19日;录用日期:2018年5月3日;发布日期:2018年5月10日

摘 要
利用Riccati-变换技巧,对二阶非线性微分方程 作进一步的研究,给出了一些新的振动准则。
关键词 :广义Riccati变换,非线性,微分方程,振动准则

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
考虑二阶非线性阻尼微分方程
(E)
其中 , , 。 , , , 。
本文仅限于研究定义在 上方程(E)存在的解。方程(E)的解称为振动的,如果它有任意大的零点;否则称它为非振动的。
方程(E)称为强次线性,如果
(1.1)
称为强超线性,如果
(1.2)
近几年来,二阶微分方程振动理论及其应用受到很大的关注,出现大量的研究论文和专著,请参考文 [1] - [6] 。特别许多学者对方程(E)的解的振动性给出了一些有效的振动准则,其中,Rgovchenko [5] 虽然对方程(E)建立了解的振动准则,但是文中对函数f作了严格的要求,即要求函数f满足条件
使得结果不能用于方程 。从而限制了它的适用范围。文 [6] 和文 [7] 建立了方程(E)新的振动准则,推广和改善了文 [5] 的结果。
本文目的同样在不要求 的条件下,建立方程(E)新的振动准则,利用不同的Riccati变换改善了文 [6] [7] 的结果,我们的结果推广和改善文 [5] [6] [7] [8] 相应结果,并以例子说明我们得到的结果的重要性,进一步说明了文 [6] [7] 的结果不能用于本文所给例子。
2. 主要结果
定义函数
(2.1)
(2.2)
考虑集合 。函数 称为属于X,记为 ,如果
(A1)
(A2)
使用一些记号定义函数, ,令
定理2.1:设函数f满足(1.1)式, ,若存在正函数 ,满足
(2.3)
且
(2.4)
则方程(E)振动。
证设方程(E)有一个非振动解 ,不妨设 ,考虑广义Riccati变换
(2.5)
(2.5)式对t进行求导,并由(E)式,知
(2.6)
不等式(2.6)两边同时乘以 ,并对此从t0到t对s进行积分,得
(2.7)
利用条件(A2),有
(2.8)
由条件(2.3)和积分中值定理知,对任意固定的 ,存在 ,使得
(2.9)
由(2.1)知,当 时,有
注意(2.1)式,于是(2.9)式可改成
(2.10)
利用(2.10)式,得到
(2.11)
联合(2.7),(2.8)和(2.11)时,得到
因此
上式与条件(2.4)矛盾,同理 时也成立,定理2.1证毕。
定理2.2设函数 满足(1.2)式,
,若存在正函数
满足(1.2)式,
,若存在正函数 ,满足
,满足
 (2.12)
(2.12)
且条件(2.4)成立,则方程(E)振动。
证设方程(E)有一个非振动解 ,如同定理2.1的证明一样,我们有(2.7)和(2.8)式对
,如同定理2.1的证明一样,我们有(2.7)和(2.8)式对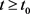 成立。
成立。
由条件(2.12)和积分中值定理,对任意固定的 ,存在
,存在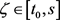 ,使得
,使得
 (2.13)
(2.13)
由(2.2)知,当 时
时

注意到(2.2)式,于是(2.13)式可改成
 (2.14)
(2.14)
利用(2.14)式,得到

此时,(2.7)式成为

因此,

上式与条件(2.4)矛盾,同理当 时结论也成立,定理2.2证毕。
时结论也成立,定理2.2证毕。
推论2.1:当 时,
时, 。若存在正函数
。若存在正函数 ,满足条件(2.12)和(2.4)式,则方程(E)振动。
,满足条件(2.12)和(2.4)式,则方程(E)振动。
证设方程(E)有一个非振动解 ,不妨设
,不妨设 ,定义函数
,定义函数
 (2.15)
(2.15)
(2.15)式对t进行求导,并由(E)式,得
 (2.16)
(2.16)
不等式(2.16)两边同时乘以 ,并对此从t0到t对s进行积分,因此
,并对此从t0到t对s进行积分,因此
 (2.17)
(2.17)
利用条件(A2),有
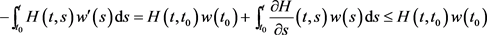 (2.18)
(2.18)
由条件(2.12)和积分中值定理知,对任意固定的 ,存在
,存在 ,使得
,使得
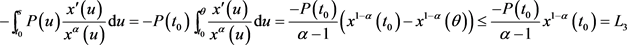 (2.19)
(2.19)
利用(2.19)式,得到
 (2.20)
(2.20)
联合(2.17),(2.18)和(2.20),有

因此

上式与条件(2,4)矛盾,同理当 时结论也成立,证毕。
时结论也成立,证毕。
注1:在方程(E)中取 。若存在正函数
。若存在正函数 使得满足
使得满足 ,且条件(2.4)成立,则方程(E)成立。
,且条件(2.4)成立,则方程(E)成立。
注2:当 时,推论2.1推广和改善了文献 [1] [2] [3] 的相应结果。
时,推论2.1推广和改善了文献 [1] [2] [3] 的相应结果。
3. 应用
例考虑二阶阻尼微分方程
 (E1)
(E1)
其中,我们取 。且取
。且取 ,则对任意
,则对任意 ,我们有
,我们有

且有

因此,

显然,方程(E1)满足条件(2.12)和(2.4),故由推论2.1知方程(E1)振动。但是,文献 [5] [6] [7] [8] 中的振动准则都不能应用于方程(E1)。
基金项目
国家自然科学基金(11271380)、茂名市科技局软科学项目(20140340; 2015038)。
文章引用
苏新晓,戴丽娜,林全文. 二阶非线性微分方程的振动准则
Oscillate Criterion for Second-Order Nonlinear Differential Equations[J]. 理论数学, 2018, 08(03): 208-214. https://doi.org/10.12677/PM.2018.83026
参考文献
- 1. Wong, J.S.W. (1973) A Second Order Nonlinear Oscillation Theorem. American Mathematical Society, 40, 487-491. https://doi.org/10.1090/S0002-9939-1973-0318585-6
- 2. Wong, J.S.W. (1986) An Oscillation Criterion for Second Order Nonlinear Differential Equations. Proceedings of the American Mathematical Society, 98, 109-112. https://doi.org/10.1090/S0002-9939-1986-0848886-3
- 3. 任崇勋, 张玉峰, 庄瑜, 俞元洪. 二阶常微分方程的一个振动定理[J]. 山东矿业学院学报, 1998, 17(1): 112-116.
- 4. 俞元洪, 靳明忠. 非线性二阶微分方程的振动定理[J]. 云南工学院学报, 1991(3): 79-84+90.
- 5. Rogovchenko, Y.V. (2000) Oscillation Theorems for Second Order Equations with Damping. Nonlinear Analysis, 41, 1005-1028. https://doi.org/10.1016/S0362-546X(98)00324-1
- 6. 俞元洪. 带有阻尼项的二阶非线性微分方程的振动准则[J]. 应用数学学报. 1993, 16(4): 433-441.
- 7. 林全文, 俞元洪. 二阶非线性振动的Philos型积分平均[J]. 数学物理学报, 2012, 32A(4): 661-669.
- 8. 林全文, 俞元洪. 带有阻尼项Emden-Fowler方程的区间振动准则[J]. 数学杂志, 2012, 32(4): 716-722.
NOTES
*通讯作者