带等级约束的多维任务调度问题 Multidimensional Task Scheduling Problem under a Grade of Service Provision

doi:10.12677/PM.2018.85064

Pure Mathematics
Vol. 08 No. 05 ( 2018 ), Article ID: 26717 , 6 pages
10.12677/PM.2018.85064

Multidimensional Task Scheduling Problem under a Grade of Service Provision

Bingfei Dai

●How to Cite this Article

School of Mathematics and Statistics, Yunnan University, Kunming Yunnan

Received: Aug. 12^th, 2018; accepted: Aug. 30^th, 2018; published: Sep. 6^th, 2018

ABSTRACT

According to vector scheduling problem and task scheduling problem under a grade of service provision, we propose multidimensional task scheduling problem under a grade of service provision. We first design a 5 d/4 approximation algorithm. Then, we give a dynamic programming algorithm and a fully polynomial time approximation scheme.

Keywords:Vector Scheduling, Dynamic Programming, A Grade of Service Provision, Approximation Algorithm

带等级约束的多维任务调度问题

代兵飞

云南大学数学与统计学院，云南昆明

收稿日期：2018年8月12日；录用日期：2018年8月30日；发布日期：2018年9月6日

摘要

根据向量调度问题和带等级约束的任务调度问题，我们提出了带等级约束的多维任务调度问题。我们首先设计了一个5 d/4-近似算法。然后，我们给出一个动态规划算法和一个完全多项式时间近似方案。

关键词 :向量调度，动态规划，服务等级，近似算法

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

向量调度问题是经典的完工时间最小化问题的推广。一般来说，向量调度问题是将n个d-维向量分配给m台机器以使得所有机器、所有维数的最大负载尽可能小。在文 [1] 中，由于Graham创造性的工作，单维负载均衡问题被广泛的研究。然而在许多问题中，一项任务可能需要不同的资源来完成，因此任务就无法用单一的量来度量。例如，如果一项任务同时需要CPU和内存，任务的需求最好用一个2-维向量来刻画，向量的每个分量对应一种资源的数目。

Chekuri和Khanna [2] 首次提出向量调度问题，算法调度d-维工件给机器加工以使得所有机器、所有维数的最大负载尽可能小。当d是任意常数时，除非 $P = N P$ ，Chekuri和Khanna证明向量调度问题不能在常数因子内近似。此外，他们 [2] 设计了一个 $O (\ln^{2} d)$ -近似算法。当d是固定常数时，他们提出了一个运行时间为 ${(n d / ε)}^{O ({(\frac{\ln (d / ε)}{ε})}^{d})}$ 的多项式时间近似方案(PTAS)。最近，Bansal等人 [3] 在 $\exp ({(1 / ε)}^{O (d \log \log d)}) + n d$ 时间内设计了一个有效的多项式时间近似方案(EPTAS)。

对于在线向量调度问题，Zhu等人 [4] 提出了一个竞争比为 $O (\log d m)$ 的在线算法。Meyerson等人 [5] 改进了文 [4] 中的算法，而且得到了一个 $O (\log d)$ -近似算法。通过给出一个在线下界，Im等人 [6] 证明 $Θ (\log d / \log \log d)$ 是在线向量调度问题的最优竞争比。

对于经典的带等级约束的离线调度问题，当机器台数m为固定常数时，Hwang等人在文 [7] 证明了LG-LPT算法的近似比：当 $m = 2$ 时为5/4，当 $m \geq 3$ 时为 $2 - 1 / (m - 1)$ 。在2007年，Glass和Kellerer在文 [8] 对离线排序问题的特殊情形：当任务的加工时间只能是1或者 $λ$ 时，证明了近似比趋于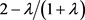。当任务的加工时间无限制时，他们给出了一个3/2-近似算法。Ou等人在文 [9] 给出了一个4/3-近似算法同时设计了一个多项式时间近似方案。Li等人在文 [10] 中对 $l_{p}$ 范数下具有等级约束的问题进行研究，并给出了一个基于线性规划解的全范数2-近似算法。

近年来，许多研究人员开始关注云计算中的资源分配问题。Liu等人在文 [11] 研究了异构物理机环境下的资源管理问题。云供应商给物理机提供异构资源，资源种类分别为CPU，存储，硬盘大小等。在实际问题中，为了提高异构资源的利用效率，一些异构资源只能分配给一些特定的物理机。受Liu等人的启发，结合文 [2] 和 [7] 的创作思想，我们提出一种新的调度模型：带等级约束的多维任务调度问题。在这里，每个多维任务和每台机器都有一个等级，我们需要把每个多维任务调度到等级不高于它的机器上加工。目标是最小化所有机器、所有维数的最大负载。明显地，当 $d = 1$ 时，带等级约束的多维任务调度问题就是经典的带等级约束的平行机调度问题。在本文，我们研究两台平行机上带等级约束的多维任务调度问题。为了便于分析，我们把这个问题简记为 $P_{2} | G o S, V C | C_{\max}$ 。

2. 预备知识

对于 $P_{2} | G o S, V C | C_{\max}$ 问题，给定实例 $I = (M, J, p, g)$ 。集合 $M = {M_{1}, M_{2}}$ 包含两台平行机。集合 $J = {J_{1}, J_{2}, \dots, J_{n}}$ 包含n项任务。每一项任务 $J_{j}$ 对应一个d-维向量 $p_{j} = (p_{j 1}, p_{j 2}, \dots, p_{j d})$ 。在这里，我们要求 $p_{j k}$ 是整数。 $g (J_{j})$ 是任务 $J_{j}$ 的等级，机器 $M_{i}$ 也有一个等级 $g (M_{i})$ 。当 $g (J_{j}) \geq g (M_{i})$ 时，任务 $J_{j}$ 可以在机器 $M_{i}$ 上加工。任务 $J_{j}$ 到达后即可开始加工，加工过程不可中断而且每项任务只需加工一次。把n项任务分配给两台机器加工，我们可以得到任务集J的一个划分 $(S_{1}, S_{2})$ 。在这里，我们令 $P_{i} = \max_{k} \sum_{J_{j} \in S_{i}} p_{j k} (i = 1, 2; k = 1, \dots, d)$ 。对于 $P_{2} | G O S, V C | C_{\max}$ 问题，我们的目标是使 $\max_{i} P_{i}$ 最小，也就是使所有机器、所有维数的最大负载尽可能小。

为了理解问题 $P_{2} | G O S, V C | C_{\max}$ 。我们给出一个例子：给定两台机器M₁和M₂，它们的等级分别为1和2。3个任务 $J_{1} = {(3, 1, 1)}^{T}$ 、 $J_{2} = {(3, 2, 5)}^{T}$ 、 $J_{3} = {(1, 0, 1)}^{T}$ ，工件的等级分别是1，2，2。对于这个实例，最优的分配方案是把任务 $J_{1}$ 和 $J_{3}$ 分配给机器M₁，任务 $J_{2}$ 分配给机器M₂，最优方案对应的最优值是5。

在实例I的基础上，我们构造实例 $\hat{I} = (M, J, \hat{p}, g)$ 。实例I与实例 $\hat{I}$ 的差别是特征p与 $\hat{p}$ ：在实例I中，任务 $J_{j}$ 对应一个d-维向量 $p_{j} = {(p_{j 1}, p_{j 2}, \dots, p_{j d})}^{T}$ 。在实例 $\hat{I}$ 中，任务 $J_{j}$ 对应一个1维向量 ${\hat{p}}_{j} = \sum_{k = 1}^{d} p_{j k}$ 。对应于实例I的目标函数，因为实例 $\hat{I}$ 的每项任务对应一个1维向量，所以实例 $\hat{I}$ 的目标是使 $\max_{i} (\sum_{J_{j} \in S_{i}} {\hat{p}}_{j})$ $(i = 1, 2)$ 最小。

3. $\frac{5 d}{4}$ -近似算法

对于实例 $\hat{I} = (M, J, \hat{p}, g)$ ，调用文 [7] 的LG-LPT算法，我们可以得到任务集J的一个调度方案 $(S_{1}, S_{2})$ 。由实例 $\hat{I}$ 和实例I的关系， $(S_{1}, S_{2})$ 也是实例 $I = (M, J, p, g)$ 的一个调度方案。对于调度方案 $(S_{1}, S_{2})$ ，我们假设实例 $\hat{I}$ 和实例I的目标值分别是 $O U T (\hat{I})$ 和 $O U T (I)$ 。我们令 $O P T (\hat{I})$ 和 $O P T (I)$ 分别表示实例 $\hat{I}$ 和实例I的最优值。

对与实例I，我们设计了一个近似比为 $\frac{5}{4} d$ -近似算法。

算法1：近似算法

步骤1：根据实例I，构造实例 $\hat{I}$ ；

步骤2：对于实例 $\hat{I}$ ，调用LG-LPT算法，我们得到调度方案 $(S_{1}, S_{2})$ ；

步骤3：对于调度方案 $(S_{1}, S_{2})$ ，实例I和实例 $\hat{I}$ 的目标值分别是 $O U T (I)$ 和 $O U T (\hat{I})$ ；

步骤4：返回 $O U T (I)$ 。

定理1：对于问题 $P_{2} | G o S, V C | C_{\max}$ ，算法1是一个 $\frac{5}{4} d$ -近似算法。

证明：根据文 [7] 的结论可知，当机器台数 $m = 2$ 时，对于实例 $\hat{I}$ ，我们有

$O U T (\hat{I}) \leq \frac{5}{4} O P T (\hat{I})$ (1)

对于某个 $S_{i}$ ，我们假设 $O U T (I) = \max_{k} \sum_{J_{j} \in S_{i}} p_{j k}$ 。根据实例I的目标函数值的定义，我们有 $O U T (I) \leq \sum_{J_{j} \in S_{i}} \sum_{k = 1}^{d} p_{j k}$ 。再根据实例 $\hat{I}$ 的目标函数值的定义，我们有 $O U T (\hat{I}) \geq \sum_{J_{j} \in S_{i}} \sum_{k = 1}^{d} p_{j k}$ 。因此，我们有

$O U T (I) \leq O U T (\hat{I})$ (2)

我们用反证法证明 $O P T (\hat{I}) \leq d O P T (I)$ ，假设 $O P T (\hat{I}) > d O P T (I)$ 。我们设 $(S_{1}^{*}, S_{2}^{*})$ 是实例I的一个最优调度方案。根据实例I的目标函数值的定义，对于任意的 $S_{i}^{*}$ ，我们有 $d O P T (I) \geq \sum_{J_{j} \in S_{i}^{*}} \sum_{k = 1}^{d} p_{j k}$ 。结合假设 $O P T (\hat{I}) > d O P T (I)$ ，我们有

$O P T (\hat{I}) > d O P T (I) \geq \sum_{J_{j} \in S_{i}^{*}} \sum_{k = 1}^{d} p_{j k}$

上式说明，如果用调度方案 $(S_{1}^{*}, S_{2}^{*})$ 求解实例 $\hat{I}$ ，我们可以得到一个比 $O P T (\hat{I})$ 更小的目标值，这与 $O P T (\hat{I})$ 的最优性矛盾，所以我们有

$O P T (\hat{I}) \leq d O P T (I)$ (3)

联立(1)式、(2)式、(3)式，我们可以得到

$O U T (I) \leq \frac{5}{4} d O P T (I)$

因此对于 $P_{2} | G o S, V C | C_{\max}$ 问题，算法1是一个 $\frac{5}{4} d$ -近似算法。

4. 动态规划算法

在这一部分，我们将给出问题 $P_{2} | G o S, V C | C_{\max}$ 的动态规划算法。对于问题 $P_{2} | G o S, V C | C_{\max}$ ，动态规划算法的设计策略是把n项任务所有可能的调度方案遍历一次，因此我们可以得到问题的最优解。

我们令 $e_{i}$ 表示第i列元素全为1，其余元素全为0的 $d \times 2$ 维矩阵。 $p_{k}$ 表示任务 $J_{k}$ 对应的向量， $p_{k} = {(p_{k 1}, p_{k 2}, \dots, p_{k d})}^{T}$ 。 $p_{k} \otimes e_{i}$ 表示向量 $p_{k}$ 与矩阵 $e_{i}$ 的第i列元素对应相乘。

比如 $p_{1} \otimes e_{2} = (\begin{matrix} p_{11} \\ p_{12} \\ ⋮ \\ p_{1 d} \end{matrix}) \otimes (\begin{matrix} 0 \\ 0 \\ ⋮ \\ 0 \end{matrix} \begin{matrix} \end{matrix} \begin{matrix} 1 \\ 1 \\ ⋮ \\ 1 \end{matrix}) = (\begin{matrix} 0 \\ 0 \\ ⋮ \\ 0 \end{matrix} \begin{matrix} \end{matrix} \begin{matrix} p_{11} \\ p_{12} \\ ⋮ \\ p_{1 d} \end{matrix})$ 。

我们用空间 $Φ_{k} (k = 0, 1, \dots, n)$ 表示分配完前k个任务后所有可能的负载矩阵集，而且空间 $Φ_{k}$ 可由空间 $Φ_{k - 1}$ 拓展得到。 $Φ_{k}$ 的元素都是 $d \times 2$ 维负载矩阵，负载矩阵的第j列,第i行表示第j台机器的第i个负载分量。 $v_{k} = \max {i | g (M_{i}) \leq g (J_{k})}$ 表示能加工任务 $J_{k}$ 的下标最大的机器的下标。

我们假设负载空间 $Φ_{k - 1} = {A_{1}, A_{2}, \dots, A_{l}}$ 。

我们下面定义 $Φ_{k} = Φ_{k - 1} + {p_{k} \otimes e_{i} | i = 1, \dots, v_{k}}$ 。

如果 $v_{k} = 1$ ，我们有 $Φ_{k} = Φ_{k - 1} + {p_{k} \otimes e_{i} | i = 1} = {A_{1} + p_{k} \otimes e_{1}, A_{2} + p_{k} \otimes e_{1}, \dots, A_{l} + p_{k} \otimes e_{1}}$ 。

如果 $v_{k} = 2$ ，我们有 $\begin{matrix} Φ_{k} = Φ_{k - 1} + {p_{k} \otimes e_{i} | i = 1, 2} \\ = {A_{1} + p_{k} \otimes e_{1}, A_{2} + p_{k} \otimes e_{1}, \dots, A_{l} + p_{k} \otimes e_{1}, \\ A_{1} + p_{k} \otimes e_{2}, A_{2} + p_{k} \otimes e_{2}, \dots, A_{l} + p_{k} \otimes e_{2}} \end{matrix}$

如果B是一个负载矩阵，我们定义B的最大元素是B中所有元素的最大值。

例如负载矩阵 $B = (\begin{matrix} b_{11} \\ b_{12} \\ ⋮ \\ b_{1 d} \end{matrix} \begin{matrix} \end{matrix} \begin{matrix} b_{21} \\ b_{21} \\ ⋮ \\ b_{21} \end{matrix})$ ，则B的最大元素为 $\max {b_{11}, \dots, b_{1 d}, b_{21}, \dots, b_{2 d}}$ 。

动态规划算法

步骤1：我们将机器和任务都按等级从低到高的顺序重新标号，使得 $g (M_{1}) \leq g (M_{2})$ 且 $g (J_{1}) \leq g (J_{2}) \leq \dots \leq g (J_{n})$ ；

步骤2：令 $Φ_{0} = {{(0)}_{d \times 2}}$ ；

步骤3：对于 $j = 1, \dots, n$ ，做如下循环

$Φ_{k} = Φ_{k - 1} + {p_{k} \otimes e_{i} | i = 1, \dots, v_{k}}$ ；

步骤4：对于 $Φ_{n}$ 中的每个矩阵，我们分别提取最大元素得到集合 $α = {c_{1}, c_{2}, \dots, c_{| Φ_{n} |}}$

然后返回集合 $α$ 中的最小值。

根据动态规划算法可知，负载空间 $Φ_{n}$ 包含了所有可能的负载矩阵，自然也包含对应于最优解的负载矩阵，所有动态规划算法可以得到问题 $P_{2} | G o S, V C | C_{\max}$ 的最优解。

定理2 当d为固定常数时，动态规划算法的运行时间为 $O (n^{2 d + 1} p_{\max}^{2 d})$ ，其中 $p_{\max} = \max_{j, k} p_{j k} (j = 1, \dots, n; k = 1, \dots, d)$ 。

证明：由于 $p_{\max} = \max_{j, k} p_{j k}$ ，则任意机器、任意维数的负载不超过 $n p_{\max}$ 。当任务 $J_{j}$ 被调度后，因为负载矩阵中的每个元素在集合 ${0, 1, \dots, n p_{\max}}$ 内取值，所以我们可以在 $O {(1 + n p_{\max})}^{2 d}$ 时间内得到当前的负载矩阵。又因为一共有n项任务，所以动态规划算法的运行时间为 $O (n {(1 + n p_{\max})}^{2 d}) = O (n^{2 d + 1} p_{\max}^{2 d})$ 。

5. 完全多项式时间近似方案

在这一部分，对于问题 $P_{2} | G o S, V C | C_{\max}$ ，当任务维数d为固定常数时，我们用动态规划算法设计了一个完全多项式时间近似方案。

定理3 当d是固定常数时，问题 $P_{2} | G o S, V C | C_{\max}$ 在 $O (n^{2 d + 1} {(\frac{d}{ε})}^{2 d})$ 时间内存在一个完全多项式时间近似方案。

证明：我们用L表示算法1求解实例I得到的目标值。根据定理1，我们有

$O P T (I) \leq L \leq \frac{5}{4} d O P T (I)$

在实例 $I = (M, J, p, g)$ 的基础上，我们构造实例 $I^{'} = (M, J, \hat{p}, g)$ 。实例I与实例 $I^{'}$ 的差别是特征p与 $\hat{p}$ ：在实例I中，任务 $J_{j}$ 对应一个d-维向量 $p_{j} = {(p_{j 1}, p_{j 2}, \dots, p_{j d})}^{T}$ 。在实例 $I^{'}$ 中，任务 $J_{j}$ 对应一个d-维向量 ${\hat{p}}_{j} = {({p^{'}}_{j 1}, {p^{'}}_{j 2}, \dots, {p^{'}}_{j d})}^{T}$ 。在这里，我们有 ${p^{'}}_{j k} = ⌊ \frac{p_{j k}}{4 ε L / 5 d n} ⌋ \cdot \frac{4 ε L}{5 d n} (k = 1, 2, \dots, d)$ 。因为 ${p^{'}}_{j k} = ⌊ \frac{p_{j k}}{4 ε L / 5 d n} ⌋ \cdot \frac{4 ε L}{5 d n}$ ，所以 ${p^{'}}_{j k} \leq p_{j k} \leq {p^{'}}_{j k} + \frac{4 ε L}{5 d n}$ 。因为动态规划可以得到实例 $I^{'} = (M, J, \hat{p}, g)$ 的最优方案 $({S^{'}}_{1}, {S^{'}}_{2})$ ，我们假设最优值 $O P T (I^{'}) = \max_{i, k} \sum_{J_{j} \in {S^{'}}_{i}} {p^{'}}_{j k} (i = 1, 2; k = 1, 2, \dots, d)$ 。假设实例I的最优方案是 $(O_{1}, O_{2})$ ，则实例I的最优值 $O P T (I) = \max_{i, k} \sum_{J_{j} \in O_{i}} p_{j k} (i = 1, 2; k = 1, 2, \dots, d)$ 。

用实例 $I^{'}$ 的最优调度方案 $({S^{'}}_{1}, {S^{'}}_{2})$ 求解实例I，我们可以得到下面的链式不等式

$\begin{matrix} \max_{i, k} \sum_{J_{j} \in {S^{'}}_{i}} p_{j k} \leq \max_{i, k} \sum_{J_{j} \in {S^{'}}_{i}} ({p^{'}}_{j k} + \frac{4 ε L}{5 d n}) = \max_{i, k} \sum_{J_{j} \in {S^{'}}_{i}} {p^{'}}_{j k} + | S_{i}^{'} | \frac{4 ε L}{5 d n} \leq \max_{i, k} \sum_{J_{j} \in {S^{'}}_{i}} {p^{'}}_{j k} + \frac{4 ε L}{5 d} \leq \max_{i, k} \sum_{J_{j} \in O_{i}} {p^{'}}_{j k} + \frac{4 ε L}{5 d} \\ \leq \max_{i, k} \sum_{J_{j} \in O_{i}} p_{j k} + \frac{4 ε L}{5 d} \leq O P T (I) + ε O P T (I) = (1 + ε) O P T (I) \end{matrix}$

当动态规划算法求解实例 $I^{'}$ 时，由于 $O P T (I^{'}) \leq O P T (I) \leq L$ ，我们只需要考虑负载不超过L的调度方案。因为任意机器的负载分量都是 $\frac{4 ε L}{5 d n}$ 的整数倍，而且一共有n项任务，因此实例 $I^{'}$ 可以在 $O (n {(\frac{5 d n}{4 ε} + 1)}^{2 d}) = O (n^{2 d + 1} {(\frac{d}{ε})}^{2 d})$ 时间内得到最优方案。

6. 结论

在本文，对于两台平行机上的 $P_{2} | G o S, V C | C_{\max}$ 问题，我们首先设计了一个5 d/4-近似算法。然后，我们给出了一个求最优解的动态规划算法和一个完全时间多项式近似方案。对于带等级约束的多维向量调度问题，当机器台数为 $m (m \geq 3)$ 时，我们以后将设计一个近似算法而且给出一个完全多项式时间近似方案。

文章引用

代兵飞. 带等级约束的多维任务调度问题
Multidimensional Task Scheduling Problem under a Grade of Service Provision[J]. 理论数学, 2018, 08(05): 480-485. https://doi.org/10.12677/PM.2018.85064

参考文献

1. Graham, R.L., et al. (1979) Optimization and Approximation in Deterministic Sequencing and Scheduling: A Survey. Annals of Dis-crete Mathematics, 5, 287-326. https://doi.org/10.1016/S0167-5060(08)70356-X

2. Chekuri, C. and Khanna, S. (2004) On Multidimensional Packing Problems. SIAM Journal on Computing, 33, 837-851. https://doi.org/10.1137/S0097539799356265

3. Bansal, N., Vredeveld, T. and Zwaan, R.V.D. (2014) Approximating Vector Scheduling: Almost Matching Upper and Lower Bounds. LATIN 2014: Theoretical Informatics, Springer, Berlin Heidel-berg.

4. Zhu, X., Li, Q., Mao, W., et al. (2014) Online Vector Scheduling and Generalized Load Balancing. Journal of Parallel & Distributed Computing, 74, 2304-2309. https://doi.org/10.1016/j.jpdc.2013.12.006

5. Meyerson, A., Roytman, A. and Tagiku, B. (2013) Online Multidimensional Load Balancing. Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques, Springer, Berlin, Heidelberg, 287-302.

6. Im, S., Kell, N., Kulkarni, J., et al. (2014) Tight Bounds for Online Vector Scheduling. 525-544.

7. Hwang, H.C., Chang, S.Y. and Lee, K. (2004) Parallel Machine Scheduling under a Grade of Service Provision. Computers & Operations Research, 31, 2055-2061. https://doi.org/10.1016/S0305-0548(03)00164-3

8. Glass, C.A. and Kellerer, H. (2007) Parallel Machine Scheduling with Job Assignment Restrictions. Naval Research Logistics (NRL), 54, 250-257. https://doi.org/10.1002/nav.20202

9. Ou, J., Leung, J.Y.T. and Li, C.L. (2008) Scheduling Parallel Machines with Inclusive Processing Set Restrictions. Naval Research Logistics (NRL), 55, 328-338. https://doi.org/10.1002/nav.20286

10. Li, W., Li, J. and Zhang, T. (2012) Two Approximation Schemes for Scheduling on Parallel Machines under a Grade of Service Provision. Asia-Pacific Journal of Operational Research, 29, 1250029. https://doi.org/10.1142/S0217595912500297

11. Liu, X., Li, W. and Zhang, X. (2018) Strategy-Proof Mechanism for Provi-sioning and Allocation Virtual Machines in Heterogeneous Clouds. IEEE Transactions on Parallel & Distributed Systems, 99, 1650-1663.

期刊菜单