Pure Mathematics
Vol.
09
No.
02
(
2019
), Article ID:
29165
,
5
pages
10.12677/PM.2019.92018
Coleman Automorphisms of Finite Groups with a Self-Centralizing Normal Subgroup
Jianxia Liu, Jinke Hai*
School of Mathematics and Statistics, Qingdao University, Qingdao Shandong

Received: Feb. 13th, 2019; accepted: Feb. 28th, 2019; published: Mar. 7th, 2019

ABSTRACT
Let G be a finite group with a self-centered normal subgroup N. In this note, we studied the effects of the properties of the self-centered normal subgroup N on the structure of the Coleman outer automorphism group of G and proved that all Coleman automorphisms of G are inner when N is under some conditions. Such Coleman automorphisms play an important role in the research of normalizer problem for integral group rings.
Keywords:Perfect Group, Almost Simple Group, Coleman Automorphism
具有自中心化正规子群的有限群的Coleman自同构
刘建霞,海进科*
青岛大学数学与统计学院,山东 青岛

收稿日期:2019年2月13日;录用日期:2019年2月28日;发布日期:2019年3月7日

摘 要
设G为具有自中心化正规子群N的有限群。在这篇注记中,我们研究了自中心化正规子群N的性质对G的Coleman外自同构群结构的影响,证明了N在某些条件下G的Coleman自同构均为内自同构。这样的Coleman自同构对研究整群环的正规化子问题有着重要的作用。
关键词 :完全群,几乎单群,Coleman自同构

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
设 为有限群, 为 的一个自同构,如果 在 的任意一个 子群上的限制等于 的某个内自同构在其上的限制,则称 为 的一个Coleman自同构。 的所有的Coleman自同构组成了 的一个子群,记为 。显然 ,称商群 为 的Coleman外自同构群,记为 。在文献 [1] 中,Hertweck和Kimmerle证明了 是交换群,给出了 是 -群的一些充分条件。在文献 [2] 中,海进科等研究了因子群的性质对有限群 的Coleman外自同构群的影响,也给出了 是 -群的一些充分条件。在文献 [3] 中,李正兴等证明了具有唯一非平凡正规子群的有限群 的Coleman自同构为内自同构。Antwerpen在文献 [4] 中研究了具有自中心化特征单的正规子群的有限群的Coleman自同构,证明了这样的群的Coleman自同构也为内自同构。在文献 [5] 中,赵文英等人也研究了具有自中心化正规子群的有限群的Coleman自同构,并给出了 的一些充分条件。其它有关Coleman自同构方面的结果可参见文献 [6] [7] 。
设 是一个有限群,我们用 表示 在整群环 上的整群环,用 表示 的单位群,用 表示 在单位群 中的正规化子。对任意 ,用 表示由 通过共轭诱导的 的自同构,记 ,令 。由文献 [8] 中的问题43知, 具有正规化子性质当且仅当 。由著名的Coleman引理知 ,所以只要能够证明 ,那么 具有正规化子性质,这促使人们去研究什么样的有限群 满足 。
称 为完全群,如果 且 。称 为几乎单群,如果存在非交换单群 ,使得 。称 为有限群 和有限群 的圈积,如果 是 和 的半直积,其中 为 个 的直积,记为 。本文我们继续研究自中心化正规子群 的性质对 的Coleman外自同构群结构的影响,证明了下面主要结果:
定理1.1:设 为有限群 自中心化的正规的子群。如果 是完全群,则 的Coleman自同构均为内自同构,即 。
定理1.2:设 为有限群 的自中心化的正规子群。如果 是几乎单群,则 的Coleman自同构均为内自同构,即 。
定理1.3:设 是 和 的圈积,其中 为有限单群, 为 阶有限群,则 的Coleman自同构均为内自同构,即 。
本文所讨论的群均为有限群。设 , ,用 表示 在 上的限制。若 且 ,则用 表示 所诱导的 的自同构。设 ,用 表示由 通过共轭诱导的 的内自同构。记 ,其中 为素数。本文使用的概念与术语是标准的,参见文献 [8] [9] 。
2. 定理的证明
定义2.1 [1] :设 , 。如果存在 ,使得 ,则称 为 上的 -中心自同构。
引理2.1 [1] :设 为单群,则存在一个素数 ,使得 的 -中心自同构为内自同构。
引理2.2 [1] :设 为几乎单群,则存在一个素数 ,使得 的 -中心自同构为内自同构。
引理2.3 [4] :设 为有限群, , 是 上的一个 -方幂阶自同构。如果存在 ,使得 , ,并且存在 的一个 -子群 ,满足 ,则 。
引理2.4 [2] :设 为有限群 的正规子群。如果 ,则 。
引理2.5 [9] :设 , 在 中的正规闭包是指 中所有包含 的正规子群的交,记为 ,即 ,则
1)
为
中包含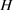 的唯一最小正规子群;
的唯一最小正规子群;
2) 。
引理2.6 [9] :设 为有限群 和有限群 的圈积,则 是 和 的半直积且 ,其中 表示群 的中心。
引理2.7:设 是有限群, 是 的 -方幂阶自同构, ,并记 。令 ,其中 为非负整数,且 。如果 ,则 。
证明:因为 是 -方幂阶的Coleman自同构,所以可设 ,其中 为非负整数。由题意可知 ,从而存在整数 ,使得 。由于 ,所以
。
因此可令 ,显然 ,故 。
定理1.1的证明:设 是 的Coleman自同构。因为 ,由引理4知 。因为 为完全群,所以 ,即存在 ,使得 。记 ,则 。由于 ,所以对任意的 ,有
,
因此 。又因为 ,所以 。由 的任意性可知 ,注意到 ,故 。
定理1.2的证明:设 是 的Coleman自同构, 为 的 -子群。由 定理知,存在 的 -子群 ,使得 。
由于 ,则存在 ,使得 。记 ,则 。因为 ,所以 。注意到且 ,由引理4知, 。因此 为 的 -中心自同构。
因为 为几乎单群,由引理2知, ,即存在 ,使得 。记 ,则 。由于 ,则对任意的 ,有
,
因此 。又因为 ,所以 。由 的任意性可知 ,注意到 ,故 。
定理1.3的证明:设 是 的 -方幂阶Coleman自同构,我们只需证 。
因为 ,并且 为 阶有限群,所以 ,其中 为 个 的直积。
设 为 的 -子群,则 为 的 -子群。由 定理知,存在 的 -子群 ,使得 。
由于 ,则存在 ,使得 。记 ,则 。令 表示 的 部分,记 ,则 是 -方幂阶的Coleman自同构且 。由于 ,所以 。
先证 为 的 -中心自同构,即证 。此处记 ,其中 ,相应的 ,其中 。因为 且 为单群,其中 ,由引理5知, ,即对任意的 ,可设 ,其中 , , ,从而
。
又因为 ,由引理4知, ,所以 。因此不妨设 ,其中 , ,所以
,
即 。这就证明了 ,因此 为 的 -中心自同构。
由于 为单群,由引理1知, ,即存在 ,使得 。又因为 ,所以存在 ,使得 。
下分两种情形进行讨论:
情形1:如果 为非交换单群,记 ,则 。因为 ,所以对任意的 ,有 ,因此 。由引理6知, ,又因为 ,所以 。由 的任意性可知 ,由于 ,所以 。注意到 ,由引理7可知, ,故 。
情形2:如果 为交换单群,那么 ,其中 为 阶循环群。因为 和 都为交换群,且 ,所以 。由于 ,则对任意的 , ,有
,
从而 。而由引理6知, 。因此任取 ,都有 ,即 。
对于这种情形,我们又可以将其分为两种情况:
① 如果 ,则 。又 , 且 是 -方幂阶的Coleman自同构,由引理3知, 。因为,由引理7可知, ,故 。
② 如果 ,则对任意 ,存在 ,使得 。因为 是 -方幂阶的,所以可设 ,其中 为非负整数,那么 ,因此 ,而 为 -群,所以 。由 的任意性可知 。又因为 ,由引理7可知, ,故 。
基金项目
国家自然科学基金(11871292)。
文章引用
刘建霞,海进科. 具有自中心化正规子群的有限群的Coleman自同构
Coleman Automorphisms of Finite Groups with a Self-Centralizing Normal Subgroup[J]. 理论数学, 2019, 09(02): 142-146. https://doi.org/10.12677/PM.2019.92018
参考文献
- 1. Hertweck, M. and Kimmerle, W. (2002) Coleman Automorphisms of Finite Groups. Mathematische Zeitschrift, 242, 203-215.
https://doi.org/10.1007/s002090100318 - 2. Hai, J.K. and Li, Z.X. (2014) On Coleman Outer Automorphism Groups of Finite Groups. Acta Mathematica Scientia, 34, 790-796.
https://doi.org/10.1016/S0252-9602(14)60049-7 - 3. Li, Z.X., Hai, J.K. and Yang, S.X. (2014) Coleman Automorphisms of Finite Groups with a Unique Nontrivial Normal Subgroup. Journal of Mathematical Research with Applications, 34, 301-306.
- 4. Antwerpen, A.V. (2018) Coleman Automorphisms of Finite Groups and Their Minimal Normal Subgroups. Journal of Pure and Applied Algebra, 222, 3379-3394.
https://doi.org/10.1016/j.jpaa.2017.12.013 - 5. 赵文英, 海进科. 关于有限内幂零群和Frobenius群的Coleman自同构[J]. 山东大学学报(理学版), 2017, 52(10): 4-6.
- 6. Hai, J.K. and Zhu, Y.X. (2018)On Coleman Automorphisms of Extensions of Finite Quasinilpotent Groups by Some Groups. Algebra Colloquium, 25, 181-188.
https://doi.org/10.1142/S1005386718000123 - 7. Hai, J.K., Ge S.B. and He, W.P. (2017) The Nor-malizer Property for Integral Group Rings of Holomorphs of Finite Nilpotent Groups and the Symmetric Groups. Journal of Algebra and Its Applications, 16, 39-44.
https://doi.org/10.1142/S0219498817500256 - 8. Sehgal, S.K. (1993)Units in Integral Group Rings. Longman Scientific and Technical Press, Harlow.
- 9. Rose, J.S. (1978) A Course on Group Theory. Cambridge University Press, Cambridge.
NOTES
*通讯作者。