Pure Mathematics
Vol.
09
No.
05
(
2019
), Article ID:
31220
,
10
pages
10.12677/PM.2019.95076
Finte Nonabelian Simple Groups and the S3-Conjecture
Yuyue Luo, Yanjun Liu*
College of Mathematics and Information Science, Jiangxi Normal University, Nanchang Jiangxi

Received: Jun. 18th, 2019; accepted: Jul. 4th, 2019; published: Jul. 11th, 2019

ABSTRACT
The S3-conjecture is a long-satnding open problem in the theory of finite groups. This paper shows that any finite nonabelian simple group has at least two conjugacy classes of same size, and so is not a counterexample to the S3-conjecture.
Keywords:Finite Groups, The S3-Conjecture, Simple Groups, Conjugacy Classes
有限非交换单群与S3-猜想
罗雨玥,刘燕俊*
江西师范大学数学与信息科学学院,江西 南昌

收稿日期:2019年6月18日;录用日期:2019年7月4日;发布日期:2019年7月11日

摘 要
有限群论中S3-猜想是一个非常古老的公开问题。本文证明了有限非交换单群至少有2个长度相同的共轭类,因此它们都不是S3-猜想的反例。
关键词 :有限群论,S3-猜想,单群,共轭类

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
有限群论是数学的一个分支,是代数学的基础组成部分。迄今为止,有限群论已经日渐完善,但仍有越来越多的问题尚待解决。近几十年,群论中的大多数公开问题及其进展都收集在The Kourovka Notebook系列丛书中,目前已经到第19版,详见 [1] 。在有限群论研究中,一个非常本质的课题是如何理解共轭类,其中Burnside、Poland、Ito等数学家特别从数量角度研究共轭类长对于群结构的影响。关于这方面研究,有一个老而著名的问题,现被称为S3-猜想,见( [1] , 16.3):
S3-猜想:若有限群G的共轭类长度各不相同,则 。
1994年,我国著名有限群论专家张继平教授 [2] 证明了可解情形下S3-猜想。1995年Knörr,Lempken 以及Thielcke [3] 也独立证明了这一情形。要特别提到的是,1994年,Arad,Muzychuk,Oliver [4] 应用特征标理论证明了如果G是S3-猜想的极小反例,那么G的非交换底柱(socle)要么平凡要么同构于下列群之一: ,,其中 ,。根据单群分类定理以及有限单群的共轭类长,本文主要证明下述定理:
定理1:任一非交换有限单群至少有两个长度相同的共轭类。因此,若非交换有限群G的共轭类长度各不相同,则G非单。
2. 预备知识
为了方便起见,本文用到的已知结论均以引理的形式给出。除特别指出,所用的记号都是标准的,参见 [5] 。
引理2.1:若 ,则 ,其中 为欧拉函数。
引理2.2:令 ,则 ,除非 为下列形式: 。
证明:这是( [6] ,引理2)。 □
引理2.3:令 ,其中 ,则 ,除非 下列形式: 。
证明:这是( [6] ,引理3)。 □
引理2.4:令q为素数方幂,l为正整数,则 ,除非 为下列形式:
1) ;2) ;3) ;4) 。
证明:这是( [6] ,引理6)。 □
引理2.5:设 或 ,则G有一个半单元素,阶为 ,并且至多分别共轭 个半单元素的幂。
证明:这是( [7] ,推论3.4)。 □
引理2.6:设 , 是 中所有与 有相同类型置换的集合,考虑 在 中的中心化子 ,则:① 当 含有一个奇置换时, 是 的一个共轭类;② 当 不含有奇置换时, 在 中分裂为以下两个长度相同的共轭类:
;
证明:这是( [10] ,定理2.7.6)。 □
3. 有限单群共轭类长
根据单群分类定理,有限非交换单群为以下群之一:离散单群、交错群、李型单群以及Tits单群,详见 [8] 。
3.1. 离散单群与Tits单群
命题3.1:设S为离散单群或Tits单群,则S至少有两个长度相同的共轭类。
证明:根据GAP [9] 直接验证可得,具体如表1。 □
3.2. 交错群共轭类长
命题3.2:对于任意的 ,交错群 至少有两个长度相同的共轭类。
证明:当n为奇数时,令 ,则 ,从而 中不含有奇置换。根据引理2.6, 在 中分裂为长度相同的两个共轭类;当n为偶数时,令
则 ,此时 也有两个长度相同的共轭类 与 。命题得证。 □
Table 1. Conjugate class lengths of discrete singletons and Tits singletons with multiplicities of at least 2
表1. 离散单群与Tits单群重数至少为2的共轭类长
3.3. 李型单群的共轭类长
本节我们考察李型单群的共轭类长。李型单群共有16族,其中典型单群为
其中 且 , 其中 且 , 其中 、 其中 、 其中 、 其中 ;
例外单群为
其中 ,,,,,,, 其中 , 其中 , 其中 。
引理3.3.1:设 ,其中 , 是素数p的方幂,则S至少有两个长度相同的共轭类。
证明:注意到 。根据( [6] ,引理17),令 ,其中f为正整数。记 是有 个元素的有限域, 为 的乘法群。由有限域的乘法群为循环群,记 为 的生成元,则 ,。令 为 的代数闭包。令G为域 上的 型单的单连通代数群,F为G中Frobenius自同态,并记 为F作用下的有限不动点群, 。记 为 的对偶,则 。
令 ,,其中 ,则
。
令 且 为自然同态,即
,
则 ,。已知 ,则
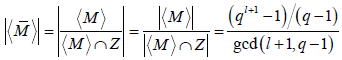 ,
,
即得 。
又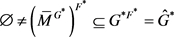 ,那么
在
及
共轭类相交非空。在它们交集中选取半单元素s,
且
,则s最多共轭于
个在
的s的幂,因此对于在
中s的本原方幂至少有
个共轭类,又
,则
。而
,故
。
,那么
在
及
共轭类相交非空。在它们交集中选取半单元素s,
且
,则s最多共轭于
个在
的s的幂,因此对于在
中s的本原方幂至少有
个共轭类,又
,则
。而
,故
。
要证S至少有两个长度相同的共轭类,即要证
而这等价于证明
记 ,由引理2.1,2.2可知 。易知 ,故S至少有两个长度相同的共轭类,除了下列情况: 及 为下列形式:
对于这些例外情形,可以直接用GAP验证 ,从而引理得证。 □
引理3.3.2:设 ,其中 , 是素数p的方幂且 ,则S至少有两个长度相同的共轭类。
证明:注意到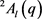 又称
,那么算
的共轭类及其长度,即算
的共轭类及其长度。若
又称
,那么算
的共轭类及其长度,即算
的共轭类及其长度。若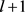 为奇数,令
为
的生成元。
,,定义
,则当l为奇数时,
为奇数,令
为
的生成元。
,,定义
,则当l为奇数时,
当l为偶数时,
即 。令 ,则 ,从而 。
令 ,由引理2.3可知, ,从而 。因此S至少有2个长度相同的共轭类,除非 为下列形式: 。而对于这些例外情形,利用GAP直接验证可得当 为 时 。对于剩余情形,即
或 ,
运行GAP程序可知 有两个长度为40的共轭类; 有两个长度为3360的共轭类; 有两个长度为1774080的共轭类。又由于 可解无需考虑,故引理得证。 □
引理 3.3.3. 设 ,其中 , 是素数p的方幂且 ,则S至少有两个长度相同的共轭类。
证明: 又称 或 ,求 共轭类及其长度即求 共轭类及其长度。令 ,根据( [7] ,推论3.4)在G中包含一个半单元素s,且 ,对于 ,有 个生成元,则s至多共轭于 个s的方幂。则s的本原方幂至少有 个共轭类,即 个共轭类,下证 。
由( [6] ,引理6)易知,
,除非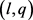 为下列形式:
为下列形式:
1) ;
2) ;
3) ;
4) ,若 ,则结论成立;对于 的情况,即 或 。
运行GAP程序可知 有2个长度为40的共轭类、 共轭类长度为40的重数大于2、 共轭类长度为255的重数大于2、 共轭类长度为13,000的重数大于2、 共轭类长度为13,000的重数大于2、 共轭类长度为262,080的重数大于2、 共轭类长度为13,000的重数大于2,即 至少有两个长度相同的共轭类。故引理得证。□
引理3.3.4:设 ,其中 , 是素数p的方幂,则S至少有两个长度相同的共轭类。
证明: 又称 、 ,求 共轭类及其长度即求 共轭类及其长度。令 ,根据( [7] ,推论3.4),在G中包含一个半单元素s,且 ,对于 有 个生成元,则s至多共轭于 个s的方幂。则s的本原方幂至少有 个共轭类,即 个共轭类,下证 。
根据( [6] ,引理6)易知, ,除非 为下列形式:
1) ;
2) ;
3) ;
4) ,若 则结论成立;对于 的情况,即
或 。
运行GAP程序可知 共轭类长度为7560的重数至少为2; 共轭类长度为364的重数至少为2; 共轭类长度为514,080的重数至少为2。即 有两个不同的共轭类长度相同。故引理得证。 □
引理3.3.5:设 ,其中 , 是素数p的方幂,则S至少有两个长度相同的共轭类。
证明: 又称 、 ,求 共轭类及其长度即求 共轭类及其长度。令 ,根据( [7] ,推论3.4),在G中包含一个半单元素s,且 ,对于 ,有 个生成元,则s至多共轭于 个s的方幂。则s的本原方幂至少有 个共轭类,即 个共轭类,下证 。
根据( [6] ,引理6)易知, ,除非 为下列形式:
1) ;
2) ;
3) ;
4) ,若 则结论成立;对于 的情况,即
运行GAP程序可知在 共轭类长度为3780的重数至少为2。即 有两个不同的共轭类长度相同,引理得证。 □
引理3.3.6:设 ,其中 , 是素数p的方幂,则S至少有两个长度相同的共轭类。
证明: 又称
,求
共轭类及其长度即求
共轭类及其长度。令
,根据( [7] ,推论3.4),在G中包含一个半单元素s,且
,对于
,有
个生成元,则s至多共轭于
个s的方幂。则s的本原方幂至少有
个共轭类,即
个共轭类,下证
。
又称
,求
共轭类及其长度即求
共轭类及其长度。令
,根据( [7] ,推论3.4),在G中包含一个半单元素s,且
,对于
,有
个生成元,则s至多共轭于
个s的方幂。则s的本原方幂至少有
个共轭类,即
个共轭类,下证
。
根据( [6] ,引理6)易知, ,除非 为下列形式
1) ;
2) ;
3) ;
4) ,若 则结论成立;对于 的情况,即
或 ,
运行GAP程序可知在 共轭类长度为9,400,320的重数至少为2、 共轭类长度为268,632的重数至少为2、 共轭类长度为609,280的重数至少为2。即 有两个不同的共轭类长度相同,引理得证。 □
引理3.3.7:设 ,其中 是素数p的方幂,则S至少有两个长度相同的共轭类。
证明:当 ,则由( [11] , p. 409), 有两个不同的共轭类 ,其长度为 ;
当 ,则由( [12] ,p. 239,表VII-1), 有 个不同的共轭类,其中 ,则有至少两个不同的共轭类 ,长度为
;
当 , 非单,无需考虑,当 时,由( [13] ,p. 364,表IV-1), 有 个不同的共轭类 ,长度为 ,引理得证。 □
引理3.3.8:群 至少有两个长度相同的共轭类,其中 是素数p的方幂。
证明:根据 [14] 可知,当 时,群 有 个不同的共轭类,它们的长度相同;当时 时,群 有 个不同的共轭类,它们的长度相同。下设 。当 时,运行GAP可知,此时群 至少有两个不同的共轭类,它们的长度相同,为69615。当 时,同样根据 [14] 可知,群 至少有 个不同的共轭类,它们的长度相同。引理得证。 □
引理3.3.9:设 ,其中 是素数p的方幂,则S至少有两个长度相同的共轭类。
证明:根据 [14] 可知,当 时,群 有 个不同的共轭类,它们的长度相同;当 时,群 有 个不同的共轭类,它们的长度相同。下设 ,由 [14] 另一数据可知,此时群 至少有 不同的共轭类,它们的长度相同,GAP运行得为共轭类长度为136592595114393600。当 时,同样根据 [14] 可知,群 至少有 个不同的共轭类,它们的长度相同。由此引理得证。 □
引理3.3.10:设 ,其中 是素数p的方幂,则S至少有两个长度相同的共轭类。
证明:根据 [14] 可知,当 时,群 有 个不同的共轭类,它们的长度相同;当 时,群 有 个不同的共轭类,它们的长度相同。下设 ,由 [14] 另一数据可知,此时群 至少有 不同的共轭类,它们的长度相同,运行GAP程序得共轭类长度为96543730483200;当 ,由 [14] 另一数据可知,此时群 至少有 不同的共轭类,它们的长度相同。故引理得证。 □
引理3.3.11:群 至少有两个长度相同的共轭类,其中 是素数p的方幂。
证明:对于 ,根据 [14] 可知,当 时,群 有 个不同的共轭类,它们的长度相同。当 时,群 有 个不同的共轭类。下面考虑 ,当 时,根据 [14] 另一张表格可知,群 有 个不同的共轭类,它们的长度相同。当 时,根据 [14] 可知有531个共轭类,有两个元素中心化子的阶为 ,则 至少有两个不同的共轭类,它们的长度相同。故引理得证。□
引理3.3.12:群 至少有两个长度相同的共轭类,其中 是素数p的方幂。
证明:对于 ,根据文献 [14] 可知,
当 时,群 有 个不同的共轭类,它们的长度相同。当 时,群 有 个不同的共轭类。当 时,根据文献 [14] 另一张表格可知,群 有 个不同的共轭类,它们的长度相同。当 时,根据文献 [14] 可知, 至少有两个不同的共轭类,它们的长度相同。引理得证。 □
引理3.3.13:群 至少有两个长度相同的共轭类,其中 是素数p的方幂。
证明:对于 ,根据( [18] ,p. 53,表4.4)可知,其中心化子的阶为
当q为偶数时,重数为
当q为奇数时,重数为
那么它们至少有2个共轭类长度相同。引理得证。 □
引理3.3.14:设 ,其中 ,则S至少有两个长度相同的共轭类。
证明:对于任意群G中的元素x及其逆元素 有
且
根据( [16] , p. 87)可知,群 有非实元素 有 ,但 位于不同的共轭类,它们所在的共轭类长度相同,即 至少有两个共轭类长度相同,由此引理得证。 □
引理3.3.15:设 ,其中 ,则S至少有两个长度相同的共轭类。
证明:同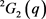 的做法,根据( [17] , p. 143, 定理13),群
有元素
,位于不同的共轭类,它们所在的共轭类长度相同。引理得证。 □
的做法,根据( [17] , p. 143, 定理13),群
有元素
,位于不同的共轭类,它们所在的共轭类长度相同。引理得证。 □
引理3.3.16:设 ,其中 ,则S至少有两个长度相同的共轭类。
证明:根据( [15] ,p. 7,表2),在 中有元素 ,,,,它们中心化子的阶相同均为 。
由群 阶为 可知,其共轭类长度相同为
,
即 至少有两个共轭类长度相同,从而引理得证。 □
命题3.3:任意李型单群至少有两个长度相同的共轭类。
证明:由引理2.3.1.~2.3.16即得。 □
定理1的证明:根据有限单群分类定理以及命题3.1~3.3即得。 □
文章引用
罗雨玥,刘燕俊. 有限非交换单群与S3-猜想
Finte Nonabelian Simple Groups and the S3-Conjecture[J]. 理论数学, 2019, 09(05): 568-577. https://doi.org/10.12677/PM.2019.95076
参考文献
- 1. Khukhro, E.I. and Mazurov, V.D. (2014) Unsolved Problems in Group Theory. The Kourovka Notebook.
- 2. Zhang, J. (1994) Finite Groups with Many Conjugate Elements. Journal of Algebra, 170, 608-624. https://doi.org/10.1006/jabr.1994.1356
- 3. Knörr, R., Lempken, W. and Thielcke, B. (1995) The S3-Conjecture for Solvable Groups. Israel Journal of Mathematics, 91, 61-76. https://doi.org/10.1007/BF02761639
- 4. Arad, Z., Muzychuk, M. and Oliver, A. (2004) On Groups with Conjugacy Classes of Distinct Sizes. Journal of Algebra, 280, 537-576. https://doi.org/10.1016/j.jalgebra.2004.03.029
- 5. Rose, J.S. (1978) A Course on Group Theory. Cam-bridge University Press, Cambridge, New York, Melbourne.
- 6. Liu, Y., Song, X. and Xiong, H. (2013) Almost Simple DD-Groups. Acta Scientiarum Naturalium Universitatis Pekinensis, 49, 741-753.
- 7. Moreto, A. (2007) Complex Group Algebras of Finite Groups: Brauer’s Problem 1. Advances in Mathematics, 208, 236-248. https://doi.org/10.1016/j.aim.2006.02.006
- 8. Gorenstein, D. (1982) Finite Simple Groups. An Introduction to Their Classification. University Series in Mathematics. Plenum Publishing Corp., New York. https://doi.org/10.1007/978-1-4684-8497-7_1
- 9. The GAP Group (2015) GAP-Groups, Algorithms, and Pro-gramming, Version 4.7.9. http://www.gap-system.org
- 10. 胡冠章. 应用近似代数(第三版)[M]. 北京: 清华大学出版社, 2006.
- 11. Chang-Ree (1972) The Characters of . In: Symposia Mathematica, Vol. VIII Convegno di Gruppi e loro Rappresentazioni, INDAM, Rome, 395-413.
- 12. Enonoto, H. (1976) The Characters of the Finite Che-valley Group , . Japanese Journal of Mathematics. New Series, 2, 191-248. https://doi.org/10.4099/math1924.2.191
- 13. Enonoto, H. and Yamada, H. (1986) The Characters of . Japanese Journal of Mathematics. New Series, 12, 325-377. https://doi.org/10.4099/math1924.12.325
- 14. Luebeck, F. () Centralizers and Numbers of Semi-Simple Classes in Exceptional Groups of Lie Type of Rank < 9. http://www.math.rwth-aachen.de/~Frank.Luebeck/chev/DegMult/index.html
- 15. Shinoda, K. (1975) The Conjugacy Classes of the Finite Ree Groups of Type (F4). Journal of the Faculty of Science, the University of Tokyo. Sect. 1 A, Mathematics, 22, 1-15.
- 16. Haroldn, W. (1966) On Ree’s Series of Simple Groups. Transactions of the American Mathematical Society, 121, 62-89. https://doi.org/10.1090/S0002-9947-1966-0197587-8
- 17. Suzuki, M. (1962) On a Class of Doubly Transitive Groups. Annals of Mathematics, 75, 105-145. https://doi.org/10.2307/1970423
- 18. Deriziotis, D.I. and Michler, G.O. (1987) Character Table and Blocks of Finite Simple Triality Groups . Transactions of the American Mathematical Society, 303, 39-70. https://doi.org/10.2307/2000778
